楽しい科学(理論)チャンネル
位相空間
位相空間に入る前に、単射、全射というものを見てみます。集合\(A\)をなす要素\(a_i\)を集合\(A\)の元といいます。
\[a_i\in A\]
で要素\(a_i\)は、\(A\)に属することを表します。\(A\)が有限個の元を持つ集合であれば、
\[A=\{a_1,\cdots,a_n\}=\{a_i\}_{i=1}^n\]
など集合\(A\)に含まれる元を用いて集合を表すこともできます。しかしこの表記はどの集合にでも使えるわけではありません。あとで説明します。集合\(A\)の任意の元\(a\)に対して、集合\(B\)の元\(b\)が1つ決まる関係を
\[f:a\mapsto b\]
と書き、写像と呼びます。また集合\(B\)の元を、\(b=f(a)\)と書くこともできます。写像\(f\)が、集合\(A\)から集合\(B\)の元を決める写像である場合、
\[f:A\to B\]
と書くことができます。
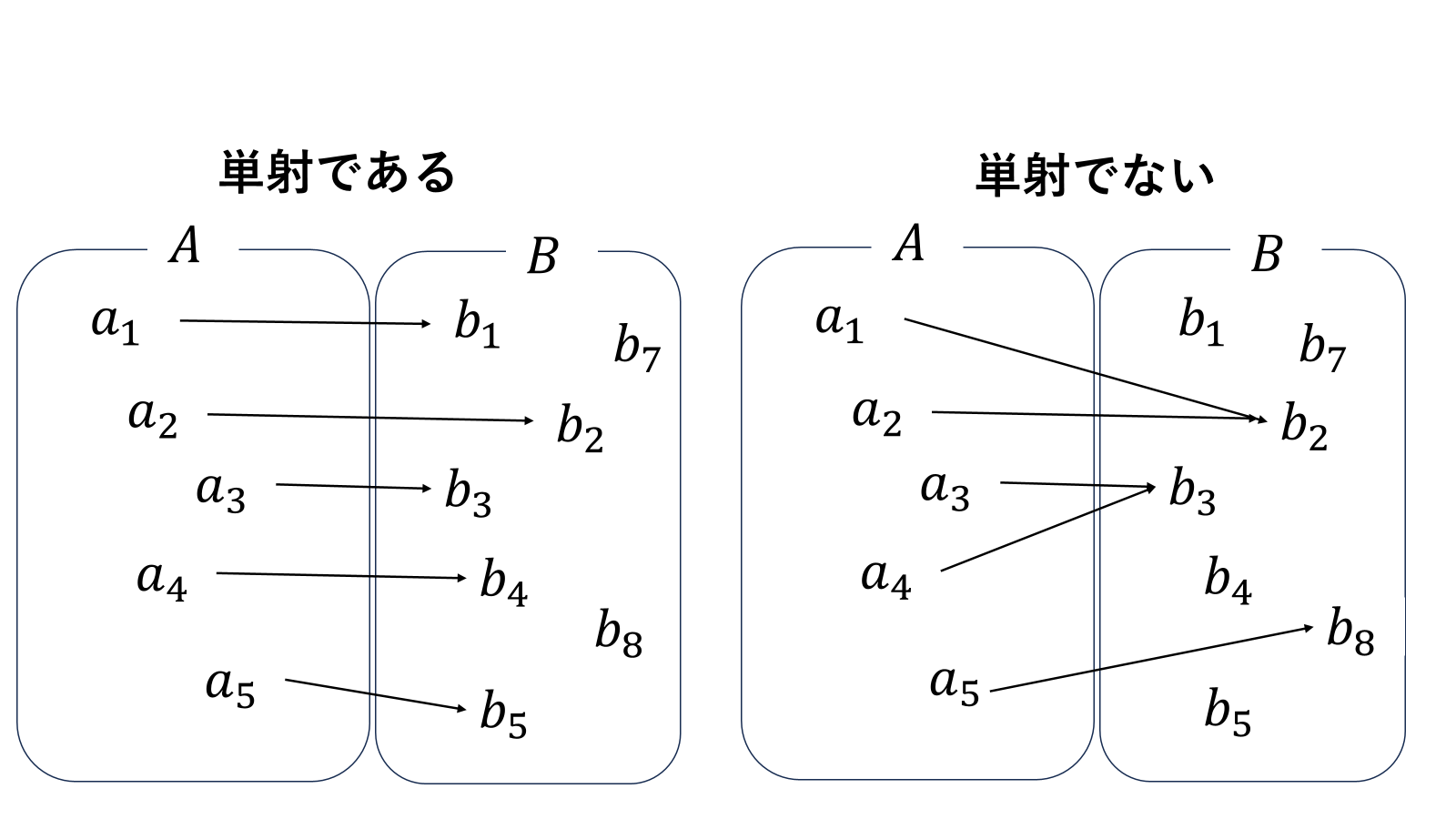
図のように単射は、集合\(A\)の任意元について、写像の終点が異なることを言います。
\[\forall a_i,a_j\in A ;\quad a_i\neq a_j\ \implies\ f(a_i)\neq f(a_j)\]
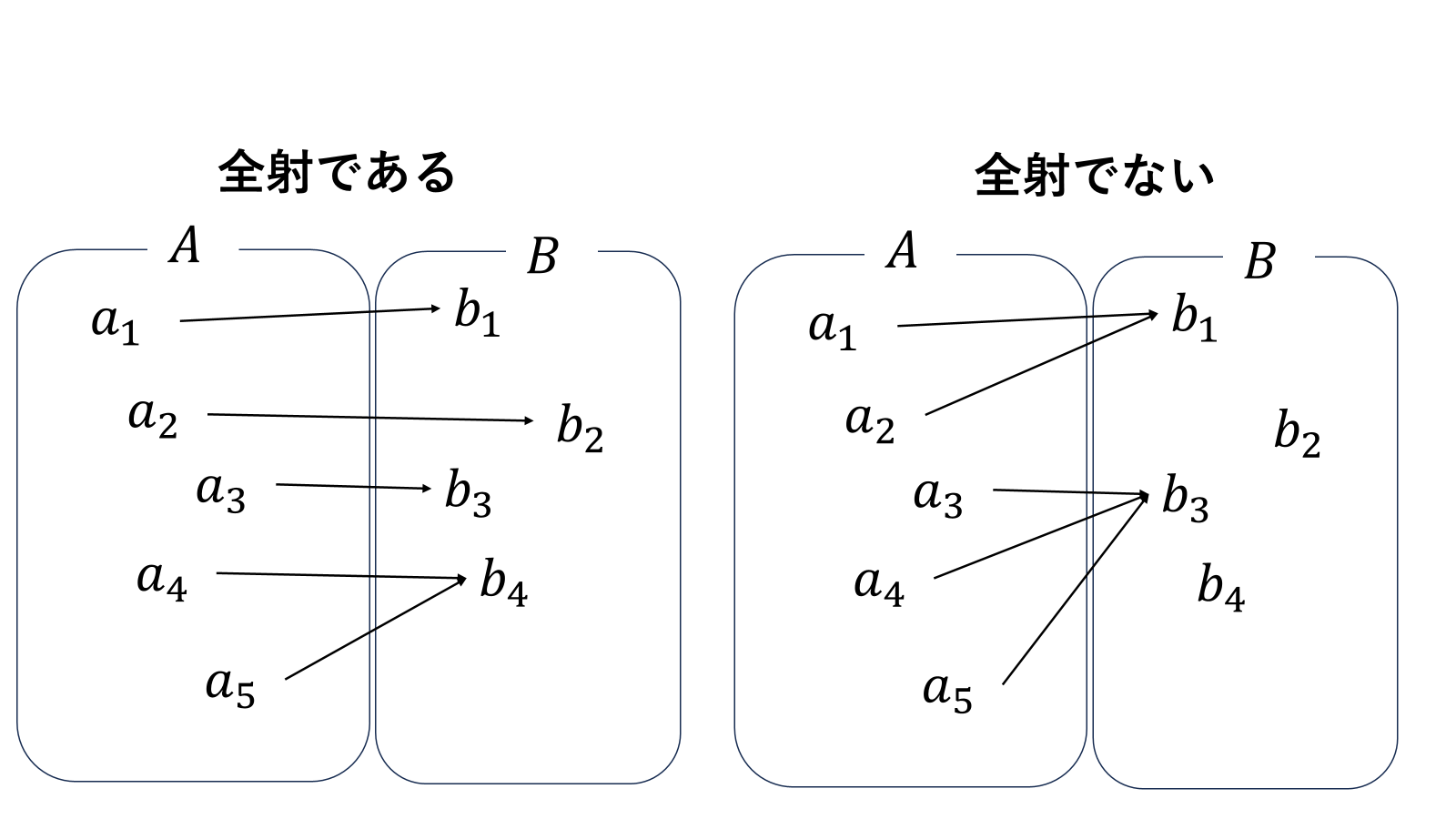
全射は、図のように、集合\(B\)の任意の元から、写像の始点(複数でもよい)が存在することを言います。
\[\exists a_i,\ \forall b_j\in B;\quad b_j=f(a_i)\]
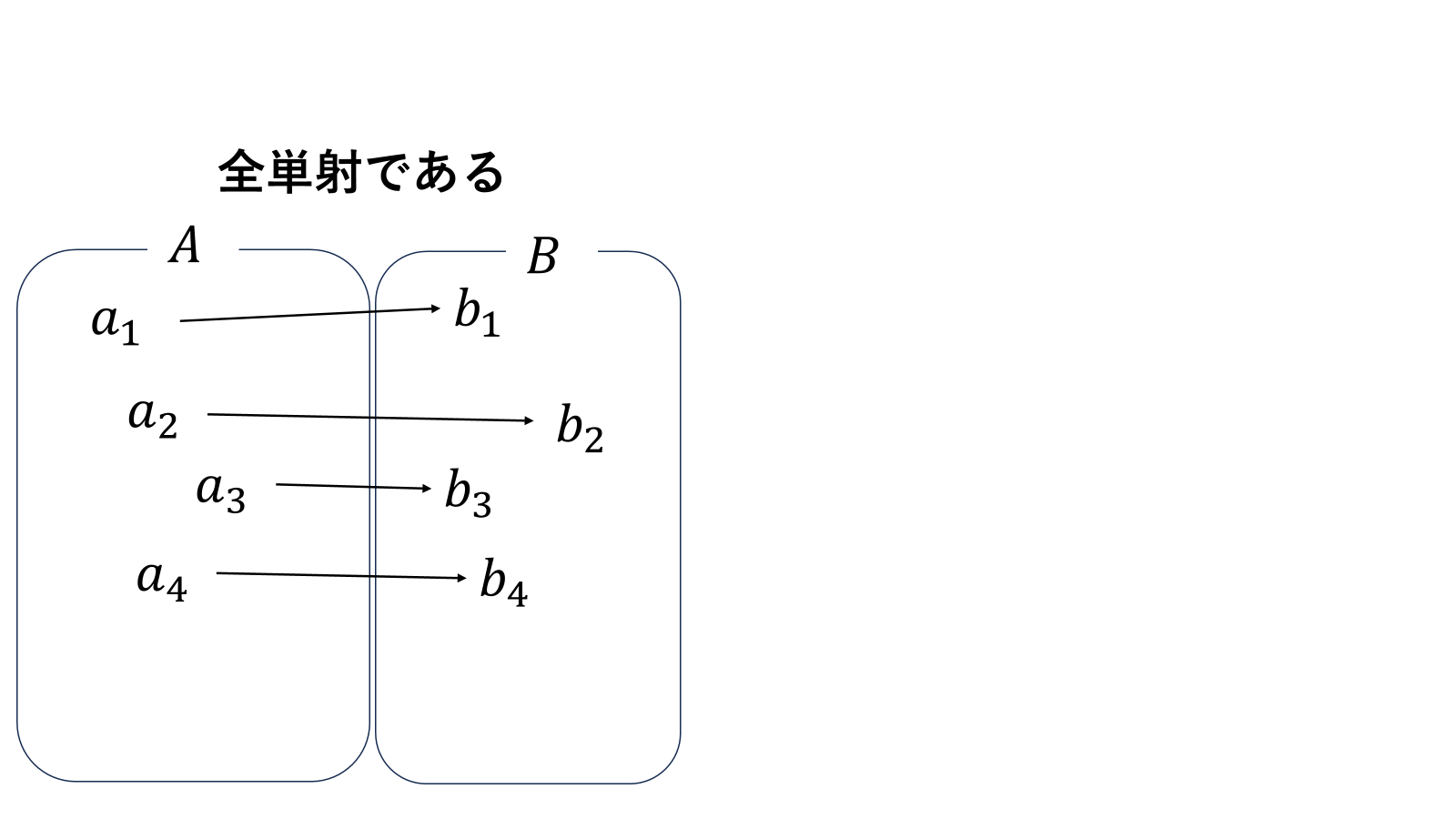
単射であり、全射である写像を全単射といいます。図より、全単射は1対1対応なので、写像の矢印を逆向きにしたものも写像となります。
\[f^{-1}:A\to B\]
\(f^{-1}\)を逆写像と呼びます。いくつか写像の例を見てみましょう。
例1
平面上で原点\(O\)から水平投射を行います。時間\(t\ge0\)と投げ出された物体の位置\((x,y)\)は全単射です。
\[f:t\mapsto (x,y)=\left(v_xt,\frac{gt^2}{2}\right)\]
時間を決めれば、物体の位置が決まりますし、物体の\(x\)座標\(x(t)\)から、時間\(t\)が決まります。
例2
自然数\(\mathbb{N}=\{1,2,3\cdots\}\)と偶数\(\{2,4,6\cdots\}\)には全単射があります。
\[f:n\mapsto 2n\]
一見自然数全体より、偶数の方が少ないような気がしますが、数学では、どちらも無限個あると考えます。\(f^{-1}(y)=\frac{1}{2}x\)の存在から、自然数も偶数も1対1対応です。
例3
自然数を実数直線上の\((0,1)\)開区間に写す全単射は存在しない。
**証明**
背理法を用います。自然数\(n\)の全単射\(f:\mathbb{N}\to(0,1)\in\mathbb{R}\)があると仮定します。\(f(n)\)をすべて小数で表します。途中で止まっても最下位の位を1減らして9を付け続けます。例えば、
\[0.5=0.499\cdots\]
\[\frac{1}{3}=0.333\cdots\]
\(0.5=0.500\cdots\)としてもいいです。しかしその場合は、ほかの有限小数にも0を付け続けます。\(0.5\)などに表記が複数あるとこの後の証明に支障が出ます。ある実数に対して、表記法が1つだけ定まるようすれば支障はありません。\(f(n)\)の小数部分を\(a_{n1}a_{n2}a_{n3}\cdots\)と書くことにします。つまり、\(a_{ij}\)は0から9のどれかの数字で
\[f(n)=0.a_{n1}a_{n2}a_{n1}\cdots\]
となります。\(f:n\mapsto f(n)\)は全単射と仮定したので、
\[f(1)=0.a_{11}a_{12}a_{13}\cdots\]
\[f(2)=0.a_{21}a_{22}a_{23}\cdots\]
\[\vdots\]
全ての自然数と\((0,1)\)開区間の数すべてが1対1対応です。ここで、
\[b_{ii}=\begin{cases}a_{ii}+1&,\mathrm{if}\ a_{ii}\lt9\\
0&,\mathrm{if}\ a_{ii}=9
\end{cases}\]
を用いて、新たに
\[f_0=0.b_{11}b_{22}b_{33}\cdots\in(0,1)\]
という数が作れます。\(b_{ii}\neq a_{ii}\)なので、\(f_0\)は\(f(n)\)とは少なくとも小数第\(n\)位が一致せず、\(f_0\)は全単射\(f\)の1対1対応から漏れています。依って仮定は誤りです。
**終わり**
三角関数をうまく使うことで、
\[f(x)=\tan 2\pi\left(x-\frac{1}{2}\right)\]
\(f:(0,1)\to\mathbb{R}\)が全単射があることが分かります。自然数、実数は、無限個あります。でも自然数と実数には1対1対応を作ることはできません。自然数くらいの無限を可算無限と呼び、実数くらいの無限を非可算無限といいます。有限個の要素を持つ集合は
\[\{a_i\}_{i=1}^n\]
と書くことができます。可算無限個の要素を持つ集合は、
\[\{a_i\}_{i=1}^\infty\]
と書くことができます。しかし非可算無限個の要素を持つ集合の要素で集合を表すことはできません。そこで非可算無限個の要素をもつ何かしらの集合集合\(I\)を用いて、
\[\{a_i\}_{i\in I}\]
などと書くことにします。ちなみにこの表記法は、添え字集合を\(I=\{1,2,3\}\)
とすれば、
\[\{a_i\}_{i\in I}=\{a_1,a_2,a_3\}\]
有限個の要素を持つ集合を表すこともできます。\(a_i\)が数である場合、添え字集合は、総和記号にも使えます。
\[\sum_{i\in I}a_i\]
添え字集合\(I\)の要素\(i\)すべての\(a_i\)を足すことを意味します。総和記号の和集合\(\cup\)、積集合\(\cap\)バージョンもあります。集合\(U_i\)について、
\[\bigcup_{i=1}^n U_i=U_1\cup U_2\cup\cdots \cup U_n\]
\[\bigcap_{i=1}^n U_i=U_1\cap U_2\cap\cdots \cap U_n\]
添え字集合を用いることもできます。
\[\bigcup_{i\in I} U_i,\quad\bigcap_{i\in I} U_i\]
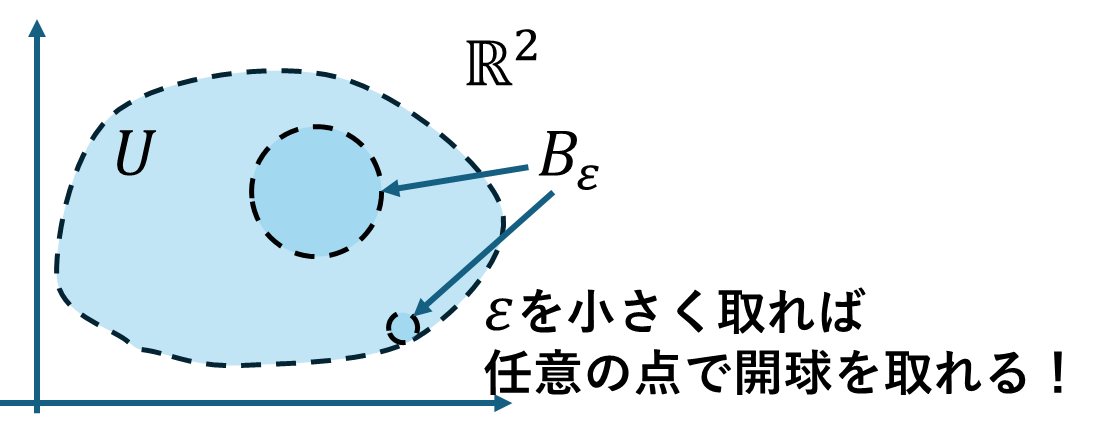
最後にユークリッド空間での開集合の定義を見ておきましょう。簡単に2次元で解説しますが、次元が高くても同じです。開球\(B_{\varepsilon}(a)\)は点\(a=(a_1,a_2)\)を中心とする半径\(\varepsilon\)の境界を含まない円盤です。
\[B_{\varepsilon}((a_1,a_2))=\left\{(x,y)\ \middle|\ \sqrt{(x-a_1)^2+(y-a_2)^2}\lt \varepsilon\right\}\]
2次元ユークリッド空間上の任意の集合\(U\)の点\(x\)を中心とする開球を取ることができるとき、その集合を開集合と定義します。
\[\exists\varepsilon\in\mathbb{R},\ \forall x\in U;\quad B_{\varepsilon}(x)\subset U \iff Uは\mathbb{R}^2上の開集合\]
では本題の位相空間に入っていきます。
**位相空間\((X,\mathfrak{O})\)の定義**
集合\(X\)部分集合\(O_\lambda\)とその集合族\(\mathfrak{O}\)について、
(1) \(X,\varnothing\in\mathfrak{O}\)
(2) 有限個の集合族\(\{O_i\}_{i=1}^n\)について、\(\begin{eqnarray}\bigcap_{i=1}^n O_{i}\in\mathfrak{O}\end{eqnarray}\)
(3) 任意の集合族\(\{O_j\}_{j\in J}\)について、\(\begin{eqnarray}\bigcup_{j\in J} O_{j}\in\mathfrak{O}\end{eqnarray}\)
を満たすとき\(O_\lambda\)を開集合、\(\mathfrak{O}\)を\(X\)の位相、\((X,\mathfrak{O})\)を位相空間と呼ぶ。
集合の集合を扱うにあたって、集合の集まりを集合族、集合系などと呼びます。(文献によってニュアンスの違いがあり?)\(X\)がどのような集合であっても位相\(\mathfrak{O}\)が定義できれば、位相空間です。ルール1は全体集合\(X\)や空集合は開集合であると定めています。ルール2は開集合の有限個の積集合は開集合になることを定めています。ルール3は開集合の非可算無限個の和集合であっても開集合であることを定めています。ここでの開集合はユークリッド空間での開集合の性質を抜き取ったもので、もっと広い意味を持ちます。位相空間の例を見ていきましょう。
例1
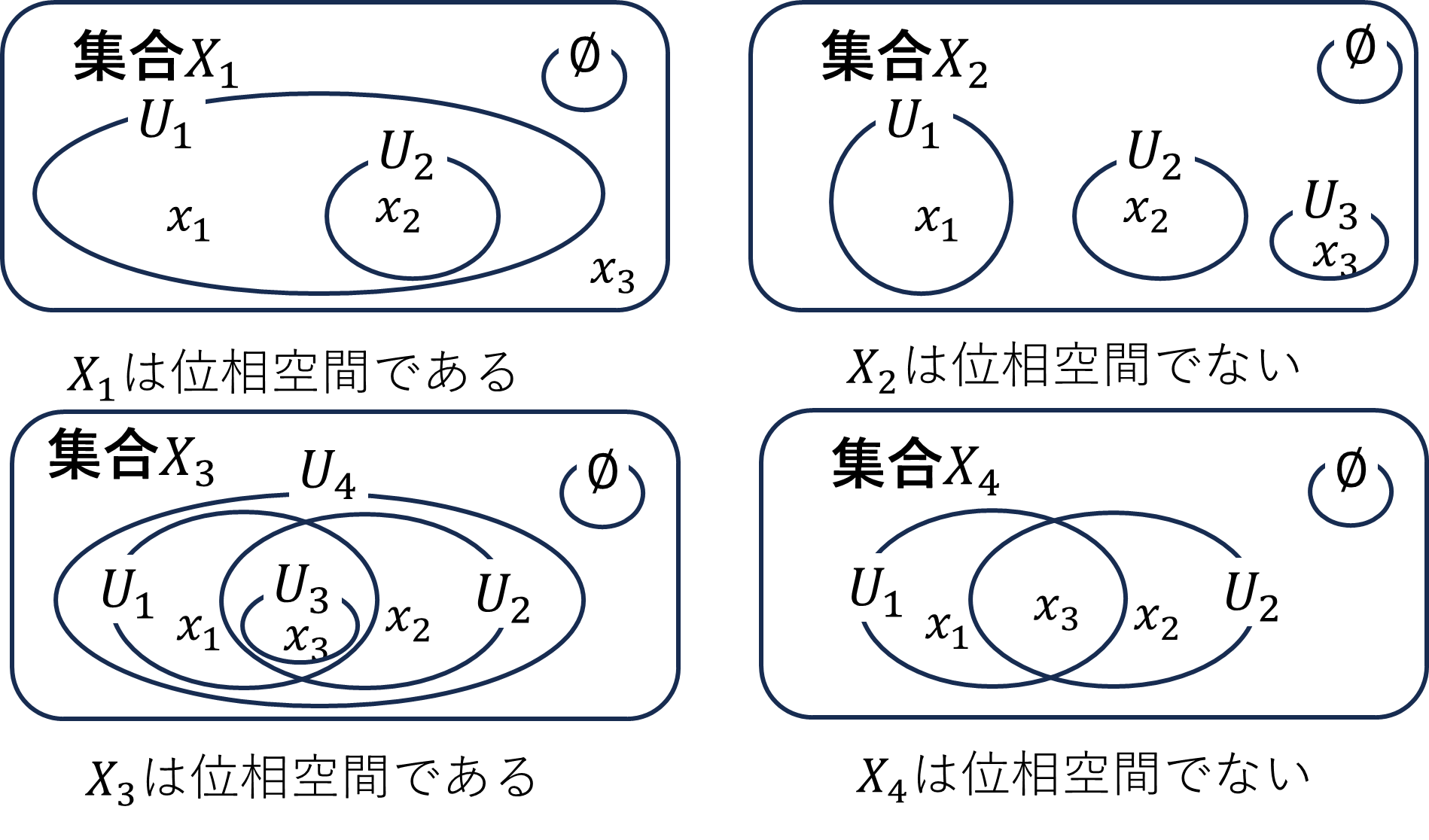
ぱっと見るとどの空間(集合)\(X_1,X_2,X_3,X_4\)が位相空間になっているか見ていきます。位相空間になっているのは、\(X_1,X_3\)だけです。ルール2、3を満たしているか列挙するのは大変なので、なにがだめで位相空間になっていないかを見ていきます。\(X_2\)では、\(U_1\cup U_2\)となる集合がありません。同様に
\[U_1\cup U_3\notin\mathfrak{O},\ U_2\cup U_3\notin\mathfrak{O}\]
なのでルール2を満たしません。そのため\(X_2\)は位相空間ではありません。\(X_3\)は
\[U_1\cup U_2\notin\mathfrak{O},\ U_1\cap U_2\]
なので、ルール2、3を満たしません。そのため位相空間にはなりません。このように有限個の要素しかない集合でも開集合を考えることができます。
例2
1次元ユークリッド空間が持つの開集合の集合系\(\mathfrak{O}_{\mathbb{R}}\)は、開集合の定められていないただの数直線\(R\)の位相となります。空集合、\(R\)は開集合となります。1次元ユークリッド空間の有限個の開集合\(\{U_i\}_{i=1}^n\)について、共通部分がない場合
\[U_1\cap\cdots \cap U_n=\varnothing\in\mathfrak{O}_{\mathbb{R}}\]
位相になります。共通部分がある場合
\[\exists x\in U_1\cap\cdots \cap U_n\]
各開集合で、\(x\)を中心とする開球
\[B_{\varepsilon_i}(x)\subset U_i\]
を取り、一番小さい\(\varepsilon_i\)について、
\[(x-\varepsilon_i,x+\varepsilon_i)\subset U_1\cap\cdots \cap U_n\]
が任意の\(x\)について、成り立つので、\(U_1\cap\cdots \cap U_n\)は開集合となります。また任意の開集合族\(\{U_j\}_{j\in J}\)について、
\[x\in\bigcup_{j\in J}U_j\]
となる任意の\(x\)について、\(x\in U_j\)となる開集合\(U_j\)があるはずなので、
\[(x-\varepsilon_j,x+\varepsilon_j)\subset U_j\]
となる\(\varepsilon_j\)を用いて、
\[(x-\varepsilon_j,x+\varepsilon_j)\subset\bigcup_{j\in J}U_j\]
が任意の\(x\)について、成り立つので、\(\bigcup_{j\in J}U_j\)も開集合です。以上から開集合の定義されていない数直線\(R\)に1次元ユークリッド空間の自然な位相\(\mathfrak{O}_{\mathbb{R}}\)を入れると\((R,\mathfrak{O}_{\mathbb{R}})\)は位相空間となります。
例3
数直線上の長さ2の線分\(L=[0,2]\)について、開集合系
\[\mathfrak{O}=\{\varnothing,\ [0,0.5),\ [0,1),\ [0,2]\}\]
は、\(L\)の位相となります。ルール1、\(\varnothing,\ L\in\mathfrak{O}\)は満たしています。ルール2を確かめます。
\[[0,0.5)\cap[0,1)=[0,0.5)\in\mathfrak{O}\]
任意の開集合\(U\)について、\(L\cap U=U,\ \varnothing\cap U=\varnothing\)は自明なので、示しません。ルール3を確かめます。
\[[0,0.5)\cup[0,1)=[0,1)\in\mathfrak{O}\]
任意の開集合\(U\)について、\(L\cup U=L,\ \varnothing\cup U=U\)は自明なので、示しません。\(\mathfrak{O}\)が\(L\)の位相になっているので\((L,\mathfrak{O})\)は位相空間です。\([0,2]\)や、\((0,1]\)は通常の\(\mathbb{R}\)の位相であれば開集合ではありません。どんな空間にどのような位相が入っているかによって開集合と呼べる集合が変わります。




