楽しい科学（理論）チャンネル

　同相という概念に入る前に連続の知識が必要になります。まずは連続についてみていきましょう。

　位相空間\((X,\mathfrak{O}_X),(Y,\mathfrak{O}_Y)\)について、写像\(f:X\to Y\)が \[\forall O_Y\in\mathfrak{O}_Y\ \Rightarrow\ f^{-1}(O_Y)\in \mathfrak{O}_X\] であるとき、\(f:X\to Y\)を連続写像という。

　注意：写像\(g:X\to Y\)が全単射の全単射の場合 \[g^{-1}:Y\to X\] が定義できました。逆像を考える際は全単射である必要はありません。逆像\(f^{-1}\)は別物です。

　ただの写像\(f:X\to Y\)について、\(Y\)の部分集合\(A\)に写る\(X\)上の点すべての集合を逆像\(f^{-1}(A)\)といいます。式で書くと、 \[f^{-1}(A)=\{x\in X\ |\ f(x)\in A\}\] となります。

　\(y=f(x)=x^2\)を例として逆像を見てみます。この写像は全単射ではありません。\(f(x)=3\)となる\(x\)は、\(x=\sqrt{3},-\sqrt{3}\)が反例です。地域\((0,1]\)の逆像は、 \[f^{-1}((0,1])=[-1,0)\cup (0,1]\] \((-2,-1)\)の逆像は、 \[f^{-1}((-2,-1))=\varnothing\] これくらいでよいでしょう。

　位相空間における連続写像は任意の開集合\(O_Y\)に対して、その逆像\(f^{-1}(O_Y)\)が位相空間\((X,\mathfrak{O}_X)\)の開集合になることを言います。位相空間における連続は、有限個の要素にも適応できますが、多様体ではあまり使わないので、位相空間における連続が、\(xy\)平面のグラフ\(y=f(x)\)が連続であることの拡張であることを見ていきます。グラフ\(y=f(x)\)が点\(a\)で連続であるとは、 \[\lim_{h\to+0}f(a+h)=f(a)=\lim_{h\to+0}f(a-h)\] 右極限と左極限が一致することを言います。

ここで開球を使ってみます。\(f(a)\)を中心とする半径\(\varepsilon\)の開球は、 \[B_{\varepsilon}(f(a))=\left\{y\ \middle|\ |f(a)-y|\lt\varepsilon\right\}\] です。この開球の逆像より小さい開球\(B_\delta(a)\)が存在する。という条件も連続を表すことができます。 \[\forall\varepsilon,\ \exists \delta;\quad B_\delta(a)\subset f^{-1}(B_\varepsilon(f(a)))\]

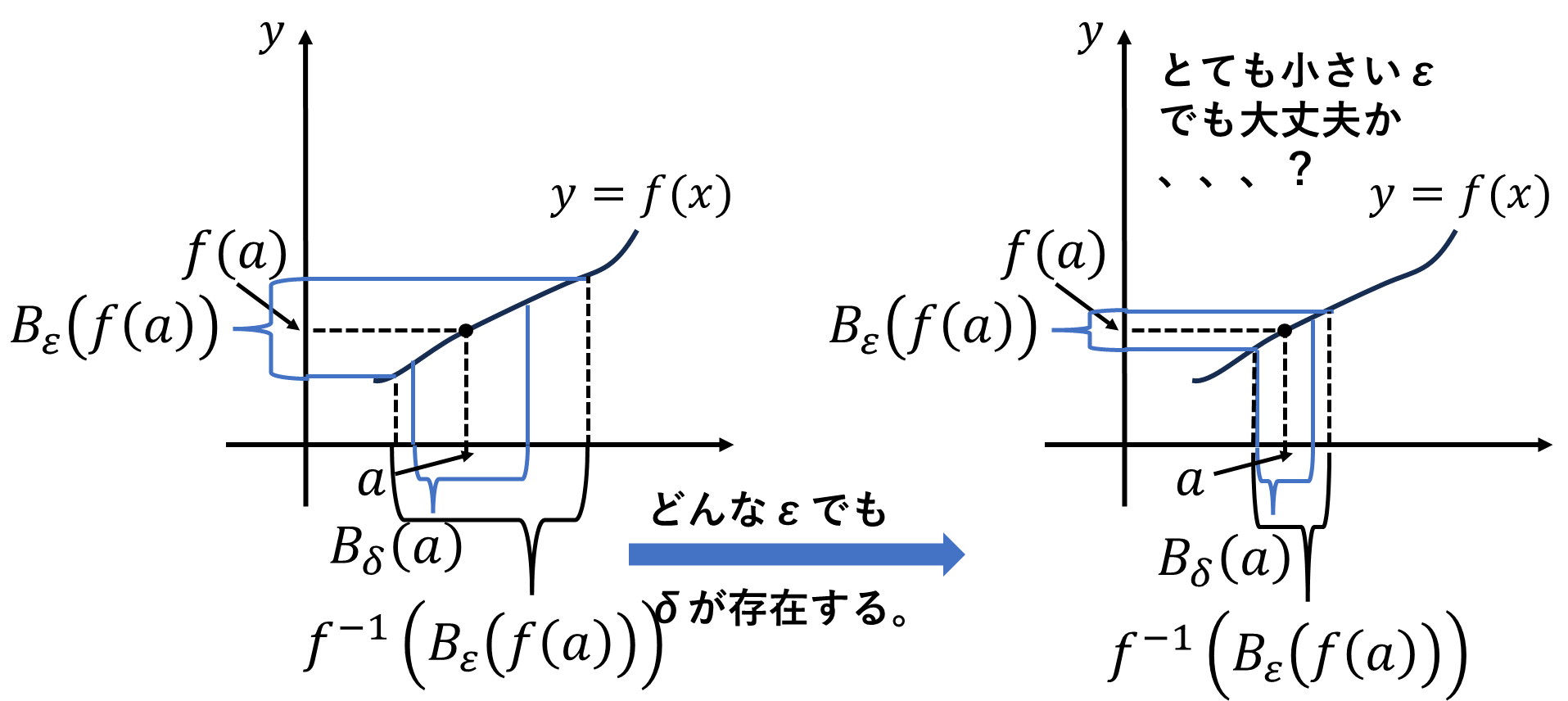
　\(\varepsilon\)-\(\delta\)による連続の定義の良い点は、多次元の開球への拡張が容易である点です。 \[B_{\varepsilon}((a^1,a^2))=\left\{(x^1,x^2)\middle|\ \sqrt{(a^1-x^1)^2+(a^2-x^2)^2}\lt\varepsilon\right\}\] これは２次元の開球です。\(x,y,z\)直交座標での曲面\(z=f(x,y)\)のグラフが点\((a^1,a^2,f(a^1,a^2))\)で連続つまり、破れや、穴がないということを、 \[\forall\varepsilon,\ \exists \delta;\quad B_\delta(a^1,a^2)\subset f^{-1}(B_\varepsilon(f(a^1,a^2)))\] ほぼ同じ式で表すことができます。写像\(f:\mathbb{R}^m\to\mathbb{R}^n\)が位相空間の意味で連続であるとき、\(\varepsilon\)-\(\delta\)の意味で連続であることを見ていきます。

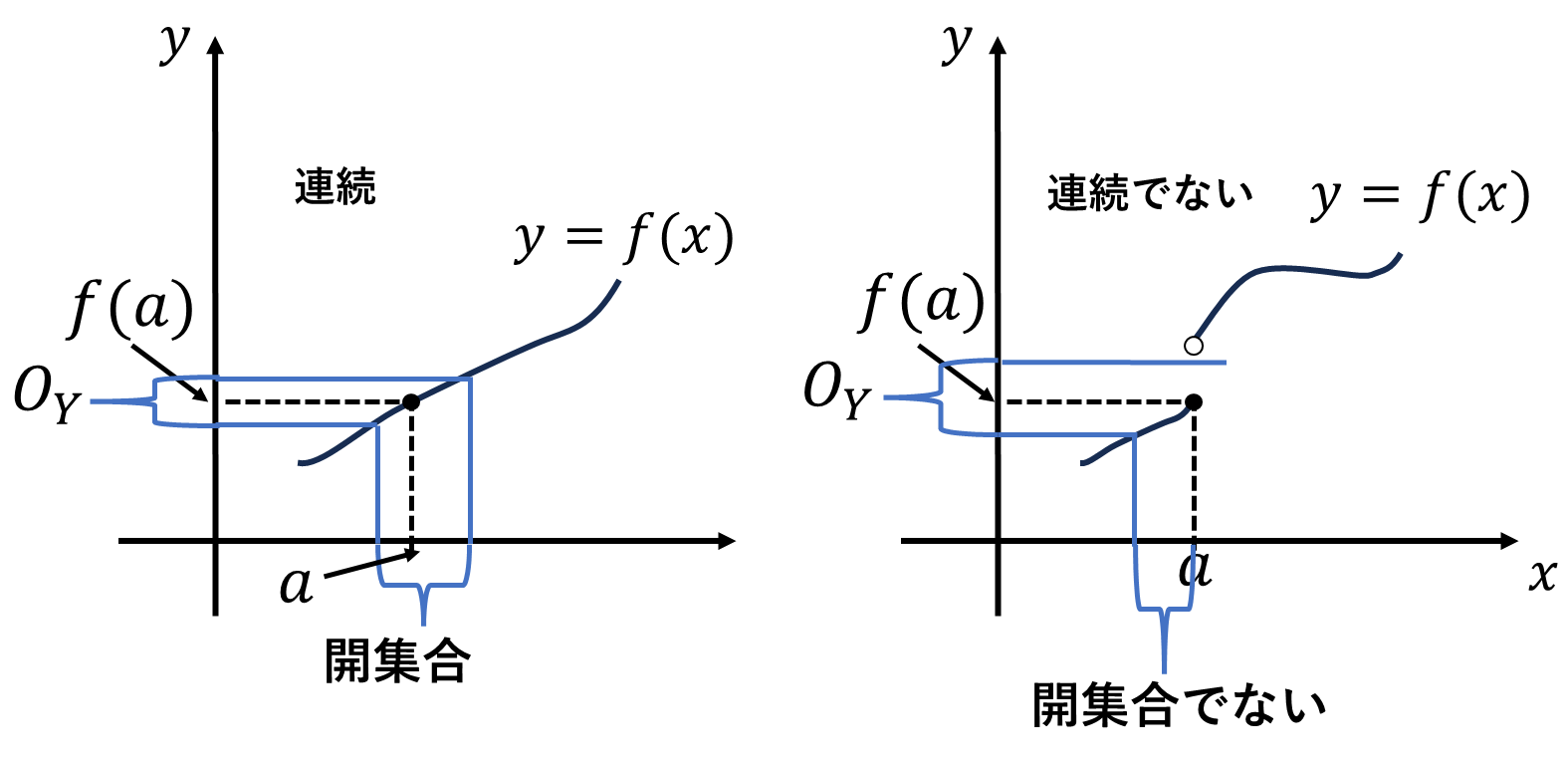
位相の意味での連続は、 \[\forall O\in\mathfrak{O}_{\mathbb{R}^n}\ ;\quad f^{-1}(O)\in\mathfrak{O}_{\mathbb{R}^m}\] 任意の開集合点\(f(a)\)を含む\(n\)次元の開球\(O=B_\varepsilon(f(a))\)で取ります。 \[\forall \varepsilon;\quad f^{-1}(B_\varepsilon(f(a)))\in\mathfrak{O}_{\mathbb{R}^m}\] \(f:a\mapsto f(a)\)なので、開球\(B_\varepsilon(f(a))\)の逆像には、点\(a\)が含まれます。更に\(f^{-1}(B_\varepsilon(f(a)))\)は開集合なので、任意の点で開球を取ることができます。点\(a\)で開球を取れば、 \[\forall \varepsilon,\ \exists\delta\ ;\quad B_\delta(a)\subset f^{-1}(B_\varepsilon(f(a)))\] \(\varepsilon\)-\(\delta\)の意味での連続が導出されます。

　位相空間\((X,\mathfrak{O}_X),\ (Y,\mathfrak{O}_Y)\)について、写像\(f:X\to Y\)が (1),(2)を満たす写像\(f\)を同相写像であるという。また位相空間\((X,\mathfrak{O}_X),\ (Y,\mathfrak{O}_Y)\)は位相同形(同位相)であるという。

　例１　同相のイメージ

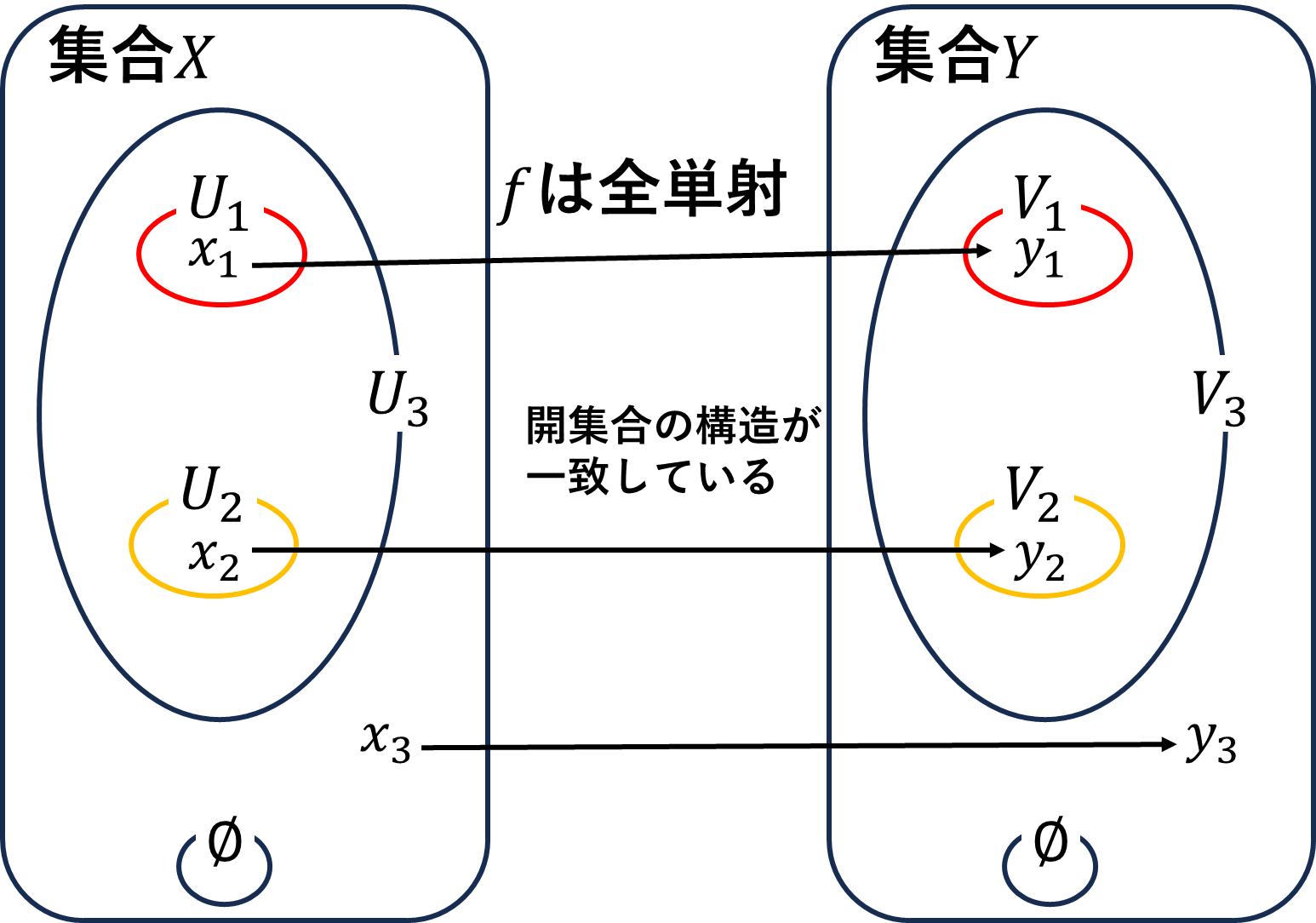
同相写像\(f:X\to Y\)の条件は２つで１つは全単射であることこれはイメージし易いです。２つ目の条件、連続写像で逆写像も連続であるこれがイメージしづらいと思います。そこで、位相\(\mathfrak{O}_X,\mathfrak{O}_Y\)がまったく同じ構造を持っているとします。そうすれば\(f^{-1}(V)\in\mathfrak{O}_X\)つまり写像\(f\)が連続であることが分かります。\(f(U)\in\mathfrak{O}_Y\)なので逆写像\(f^{-1}\)も連続であることが分かります。同相写像は、全単射で位相の構造が一致すると言い換えるとイメージしやすいかもしれません。

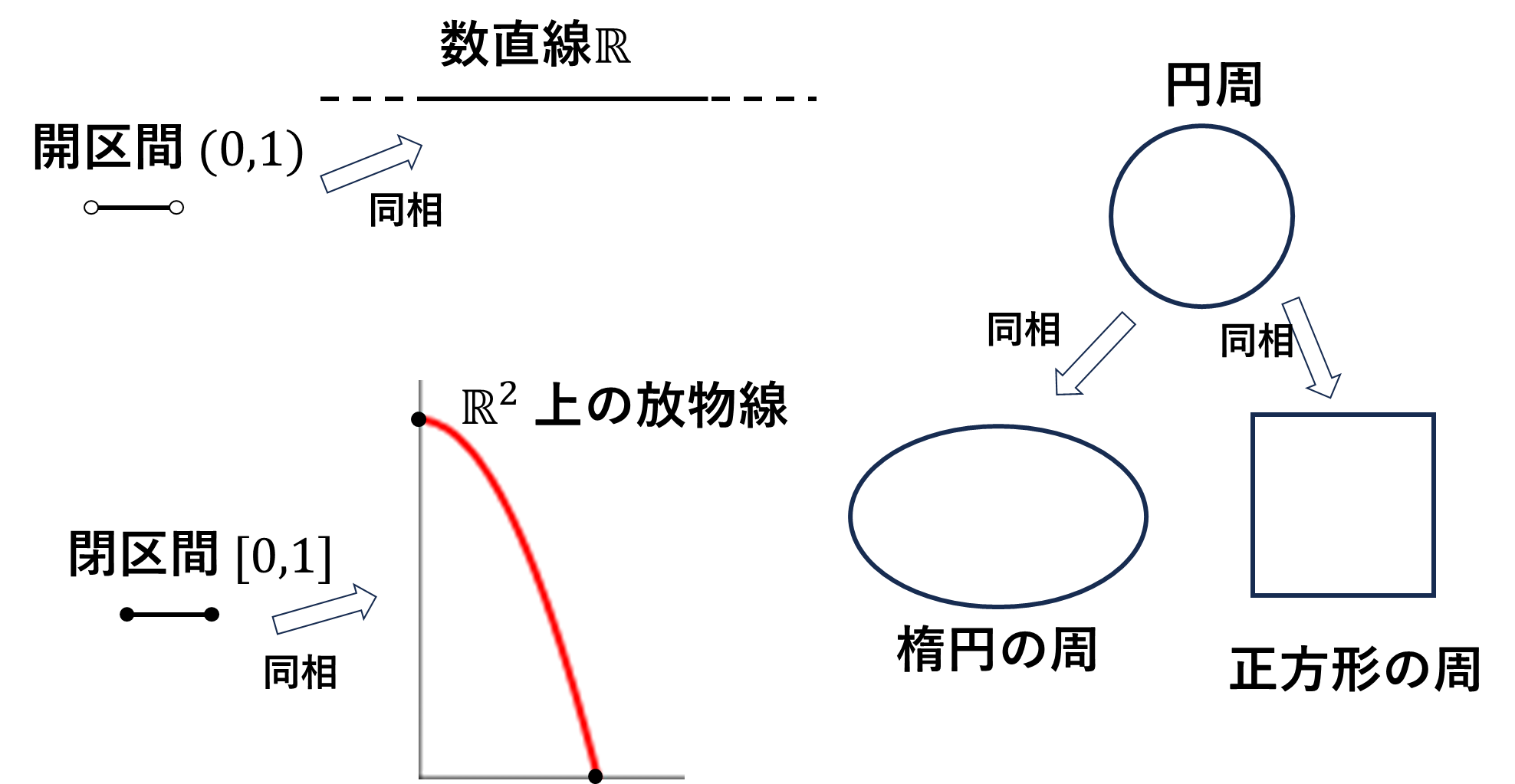
　例２　まずは簡単に\((0,1)\)開区間が実数直線\(\mathbb{R}\)と同相であることを見てみます。写像\(f:(0,1)\to\mathbb{R}\)を \[y=f(x)=\tan\left(x-\frac{1}{2}\right)\pi\] \(0\lt x \lt 1\)の範囲で逆関数 \[x=f^{-1}(y)=\frac{1}{\pi}\arctan y+\frac{1}{2}\] があり全単射です。更に\(f:(0,1)\to\mathbb{R}\)は連続写像なので、\((0,1)\)と\(\mathbb{R}\)は同相です。

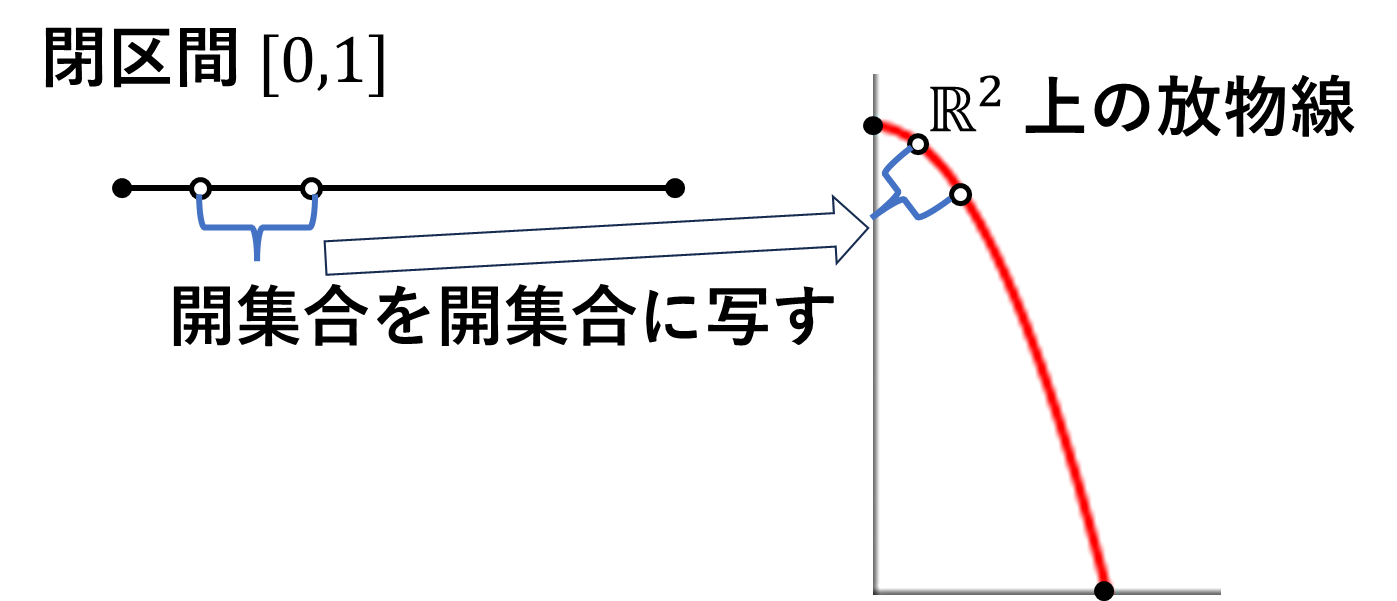
　例３　\([0,1]\)閉区間と放物線の一部 \[C=\{(x,y)\ |\ y=-x^2,\ x\in[0,\sqrt{h}]\}\] が同相であることをみていきます。例えば\(\xi\in[0,1]\)について \[(x,y)=\varphi(\xi)=(\varphi_x(\xi),\varphi_y(\xi))=(\sqrt{h}\xi,-h\xi^2)\] このような同相写像を定めればいいです。この写像は全単射で\([0,1]\)の任意の開集合に1対1で対応する放物線の開集合があるので(確認しませんが。)\([0,1]\)と\(y=-x^2\)は同相です。

　例４　円周\(S^1\)と楕円の周\(E^1\)が同相であることを見ていきます。半径１の円周は \[S^1=\left\{(x^1,x^2)\ \middle|\ (x^1)^2+(x^2)^2=1\right\}\] 楕円の周は \[E^1=\left\{(y^1,y^2)\ \middle|\ \frac{(y^1)^2}{a^2}+\frac{(y^2)^2}{b^2}=1\right\}\] これらの同相は簡単に示せます。同相写像\(\varphi:S^1\to E^1\)を \[(y^1,y^2)=\varphi(x^1,x^2)=(ax^1,bx^2)\] と定めればいいですね。

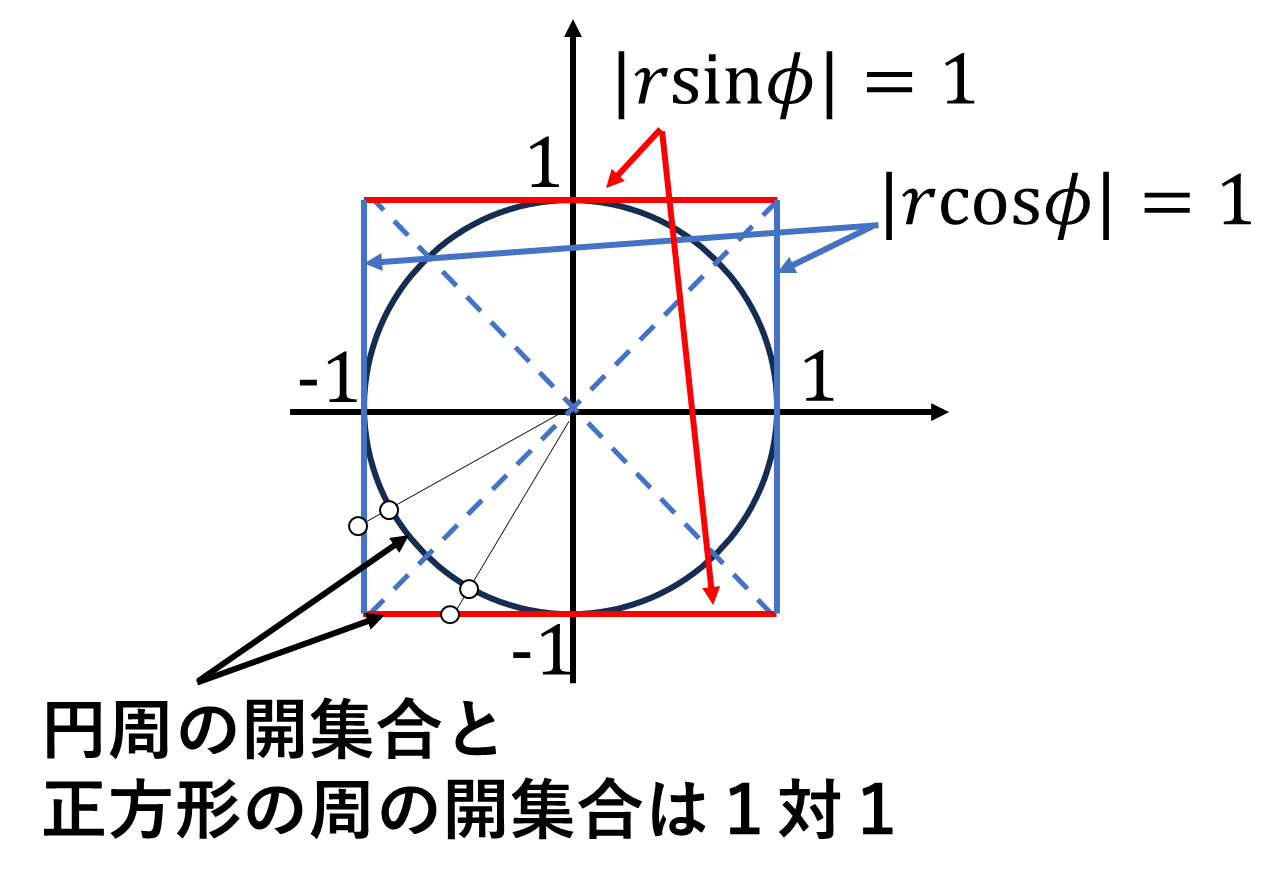
　例５　正方形の周と円周も同相です。正方形の周上の点を\((r,\phi)\)と表すことにします。すると円周上の点は\((1,\phi)\)となります。青色の線上では\(|x|=|r\cos\phi|\)が常に1であり、赤色の線上では\(|y|=|r\sin\phi|\)が常に1なのでこれを\(r\)について解けばいいです。写像\(\varphi\) \[\varphi:(1,\phi)\mapsto(r,\phi)\] \[\varphi((1,\phi))=\begin{cases}(\frac{1}{\cos\phi},\phi)&-\frac{\pi}{4}\le\phi\le\frac{\pi}{4} \\(\frac{1}{\sin\phi},\phi)&\frac{\pi}{4}\lt\phi\le\frac{3\pi}{4} \\(-\frac{1}{\cos\phi},\phi)&\frac{3\pi}{4}\lt\phi\le\frac{5\pi}{4} \\(-\frac{1}{\sin\phi},\phi)&\frac{5\pi}{4}\lt\phi\le\frac{7\pi}{4}\end{cases}\] は全単射です。なぜなら、原点から任意の方向に半直線を伸ばして、円周を通る点\((1,\phi)\)、更に正方形の周を通る点を\((r,\phi)\)とする写像なので、１対１対応になっています。

　例６　円周\((0,1)\)と\([0,1]\)は同相でない。

　例７　円周\(S^1\)と\([0,\pi)\)は同相でない。

　例６、例７を示すにはさらに位相の勉強(連結、コンパクトなど)をする必要がありますが、ここでは、同相写像を見つけられなかったら同相でないということにしておきます。図形\(A\)を伸ばしたり曲げたり(切ったり、くっ付けたりはダメ。)して図形\(A'\)に一致させられたら同相というイメージにとどめておきます。