楽しい科学(理論)チャンネル
\(m\)次元多様体
前回、位相空間の同相写像というものをやりました。開区間や閉区間、数直線に勝手に座標を入れて更に位相空間とみなしてきましたが、位相空間には座標系は入っていません。位相空間は、点の集合\(X\)とそれに開集合系\(\mathfrak{O}\)を定めただけのものです。点の数も有限かもしれませんし、開集合\(O\)が好きに取れるわけでもありません。そこで、微積分が定義できるように局所的にユークリッド空間と似た空間にします。前回、ユークリッド空間の図形を例にとった同相写像を扱ったのは多様体のイメージを掴むためです。
**\(m\)次元多様体の定義**
\(M\)を位相空間とする。
(i) ハウスドルフ性
\(M\)上の任意異なるの2点\(a,b\)について開集合\(a\in U,b\in V\)を交わらないように取ることができる。
(ii) 座標近傍
\(M\)上の任意の点\(p\)を含む開集合(開被覆)\(U_\lambda\)について\(\mathbb{R}^m\)上の開集合\(V_\lambda\)への同相写像(局所座標)\(\varphi_\lambda:U_\lambda\to V_\lambda\)がある。同相写像と開集合の組\((U_\lambda,\varphi_\lambda)\)を座標近傍(チャート)という。座標近傍を族とする集合
\[\mathcal{S}=\{(U_\lambda,\varphi_\lambda)\}_{\lambda\in\Lambda}\]
を座標近傍系(アトラス)という。(i),(ii)を満たす位相空間\(M\)とアトラス\(\mathcal{S}\)の組を、\(m\)次元多様体\((M,\mathcal{S})\)と呼ぶ。
(iii) 座標変換
2つの座標近傍\((U_1,\varphi_1),\ (U_2,\varphi_2)\)が重なりがある場合\(U_1\cap U_2\neq\varnothing\)、
\[\varphi_2\circ\varphi_1^{-1}:\varphi_1(U_1\cap U_2)\to\varphi_2(U_1\cap U_2)\]
を座標近傍\((U_1,\varphi_1)\)から\((U_2,\varphi_2)\)への座標変換という。
これだけでは意味が分からないと思うので、例を見てみましょう。
(例1) 2次元平面\(R^2\)
2次元平面\(R^2\)は2次元多様体です。どのようにアトラスを構成してもいいのですが、2次元平面上の点\(p\)を2次元ユークリッド空間にそのまま写す写像
\[\varphi:p\mapsto(x,y)\]
という恒等写像(そのまま写す写像)を取ればチャート\((R^2,\varphi)\)1つだけを族とするアトラス\(\mathcal{S}=\{(R^2,\varphi)\}\)を構成し、多様体となります。
(例2) \((0,1)\)開区間
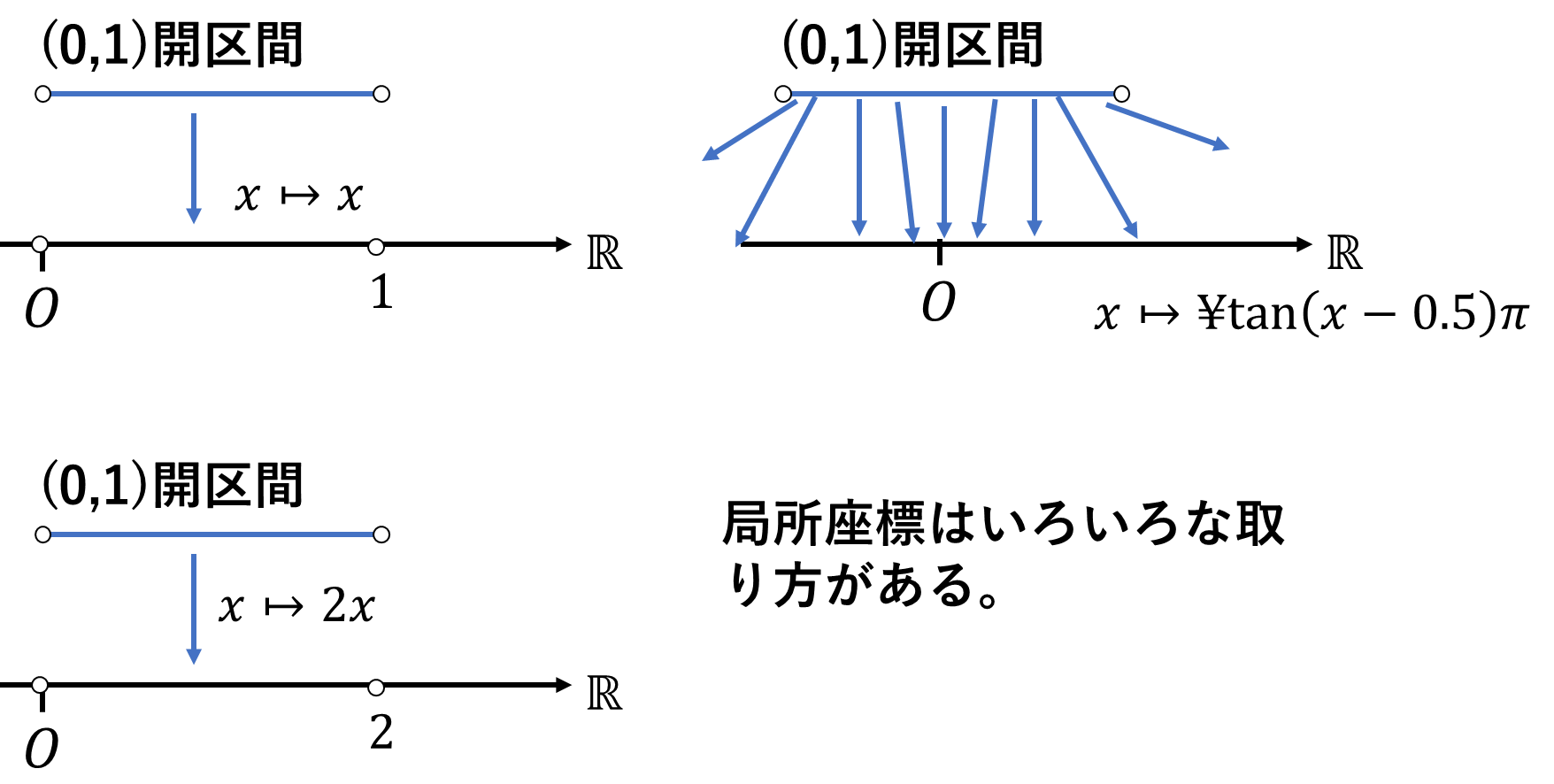
局所座標にはいろいろな取り方があります。\((0,1)\)開区間から\(1\)次元ユークリッド空間の開集合への同相写像の例をあげると、
\[\varphi_1(x)=x,\ \varphi_1:(0,1)\to(0,1)\]
\[\varphi_2(x)=2x,\ \varphi_2:(0,1)\to(0,2)\]
\[\varphi_3(x)=\tan\left(x-\frac{1}{2}\right)\pi,\ \varphi_3:(0,1)\to\mathbb{R}\]
\(\varphi_1,\varphi_2,\varphi_3\)はどれも局所座標です。
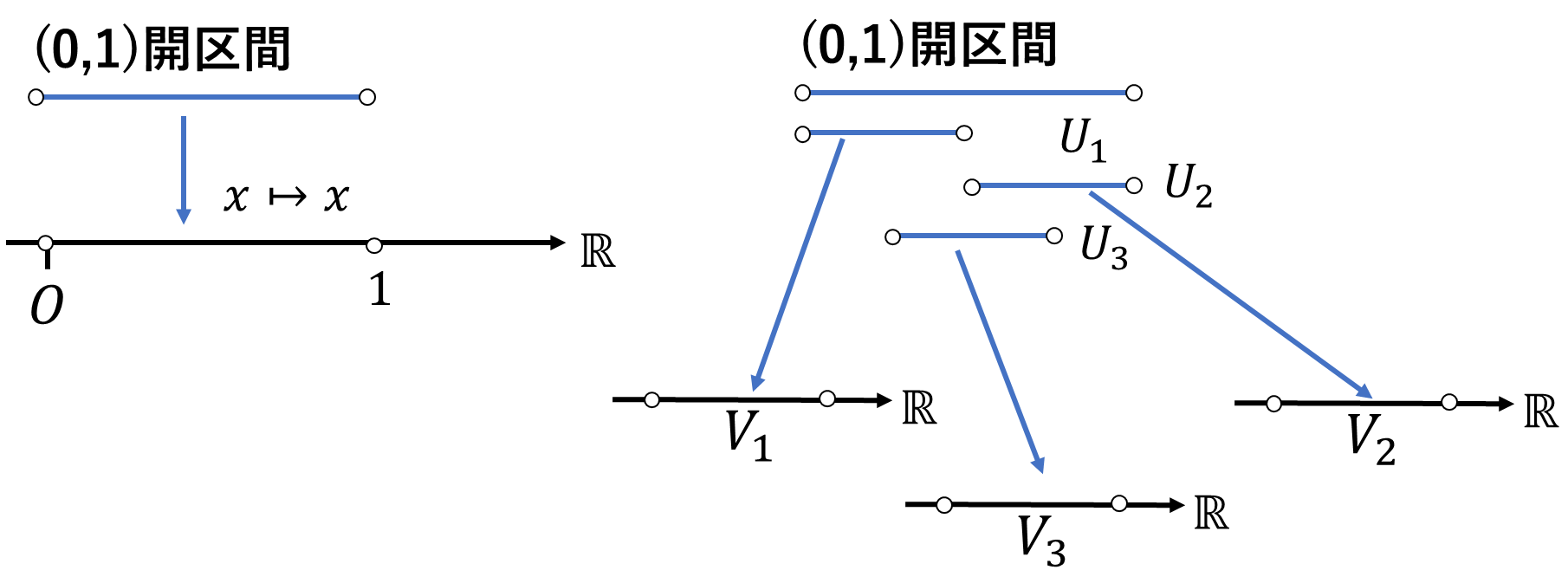
アトラスも様々なものが考えられます。\((0,1)\)開区間そのものを1つの開区間とみなして
\[\mathcal{S}=\{((0,1),\varphi_1)\}\]
としてもいいですし、図のように3つの開被覆を用意して
\[\mathcal{T}=\{(U_1,\varphi_1),(U_2,\varphi_2),(U_3,\varphi_3)\}\]
このようなアトラスを作ることもできます。多様体上の任意の点がいずれかの開被覆\(U_\lambda\)に含まれていてそれが\(\mathbb{R}^m\)上の開集合との同相写像\(\varphi_\lambda\)であれば、チャート\((U_\lambda,\varphi_\lambda)\)の集合\(\mathcal{S}\)はどのようにとっても良いのです。
(例3) 円周\(S^1\)
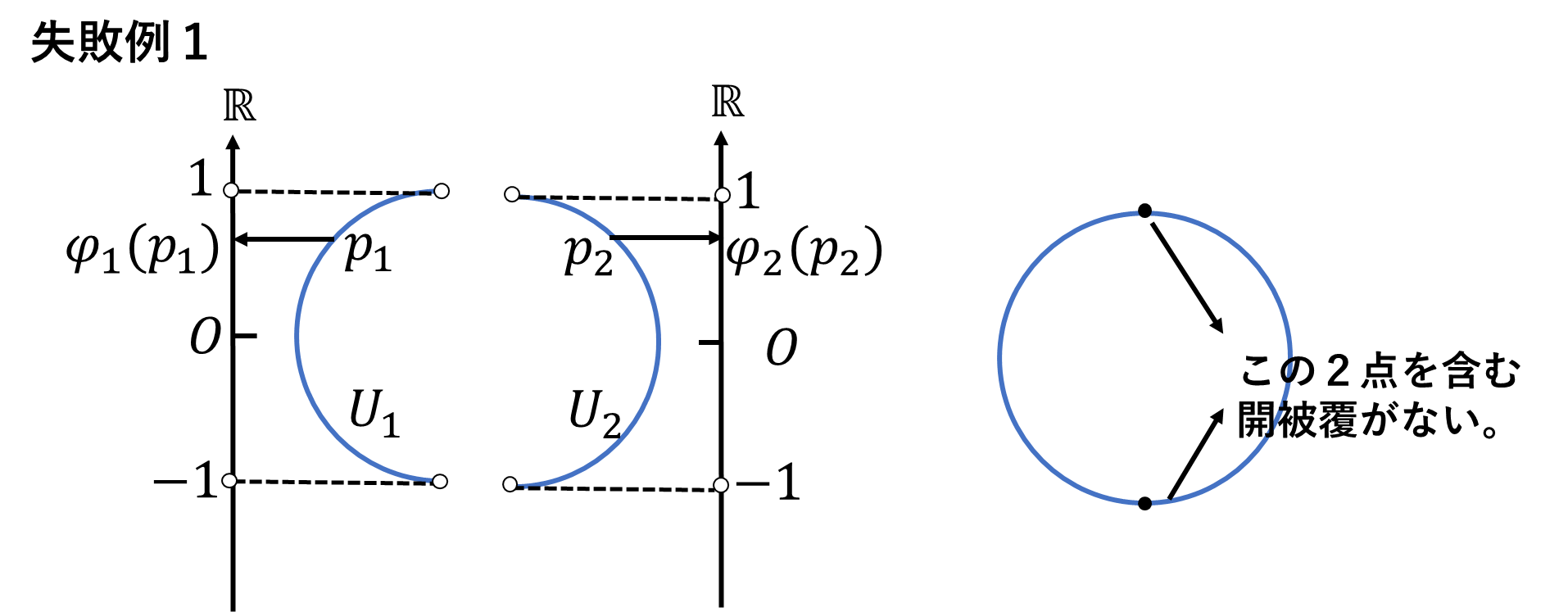
まずは失敗例をいくつか見てみましょう。円周\(S^1\)に図のような開集合\(U_1,U_2\)とその\(\mathbb{R}\)への同相写像\(\varphi_1,\varphi_2\)と取ります。\(U_1,U_2\)は\(S^1\)上の開集合で\(\varphi_1(U_1),\varphi_2(U_2)\)はユークリッド空間の開集合となるので、\((U_1,\varphi_1),(U_2,\varphi_2)\)はチャートの条件を満たしています。しかしこれらだけを族とする\(\mathcal{S}=\{(U_1,\varphi_1),(U_2,\varphi_2)\}\)はアトラスとはいえません。2点だけその点を含む開被覆がないからです。多様体は開被覆でおおわれている必要があります。記号で書くと、
\[M=\bigcup_{\lambda\in\Lambda}U_\lambda\]

円周を1のチャートで表すことはできません。これは円周\(S^1\)と\(\mathbb{R}\)上の開区間が同相でないためです。連続な全単射を考えると、必ず1点だけうまく対応しません。よく円周全体の点をラジアン\(\theta\in\mathbb{R}\)と対応させますが、局所座標という観点から見ると良くないです。(0と\(2\pi\)を同一視すればいいですが、\(\mathbb{R}\)上では\(0\lt2\pi\)の不等式の関係にあります。)
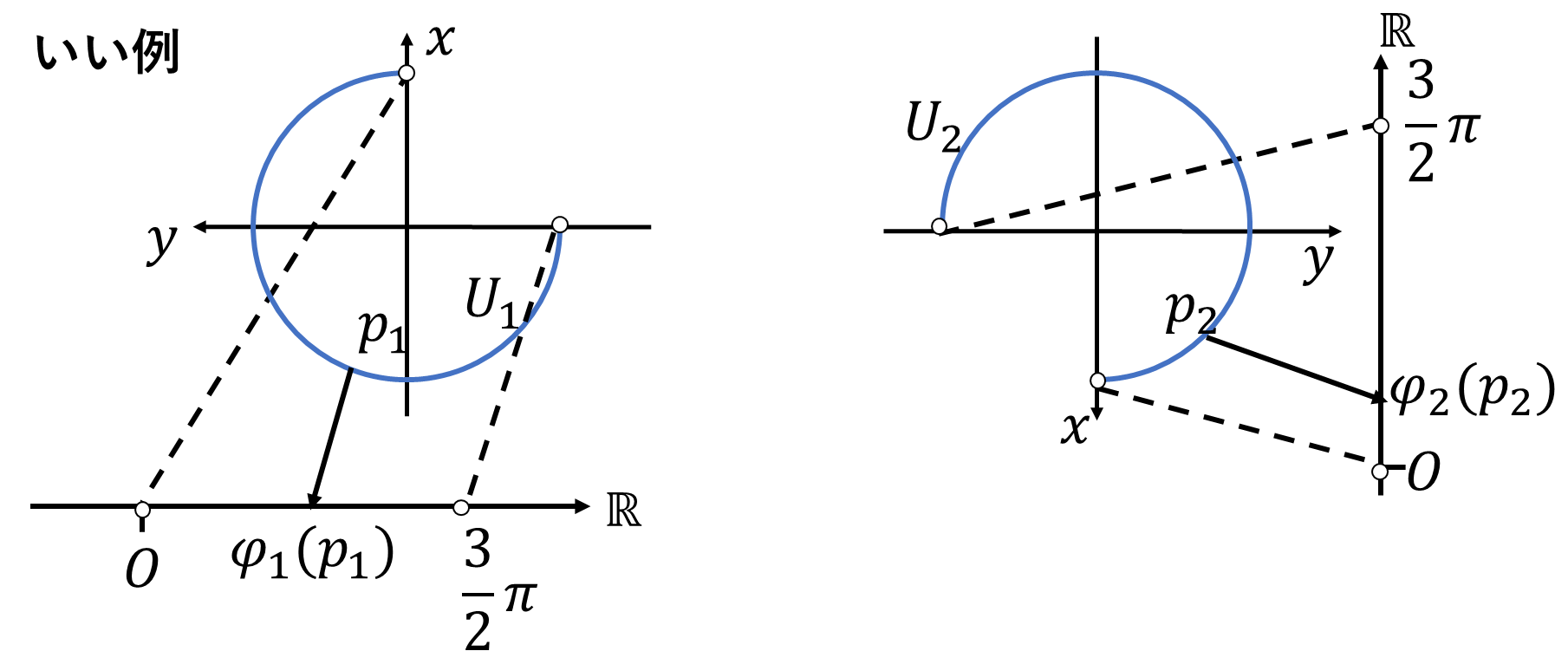
円周の開被覆\(U_1,U_2\)図のように取ります。円周の中心を原点とするユークリッド平面を仮定して極座標を取ります。\(U_1\)上の点を\((\cos\theta_1,\sin\theta_1)\)、\(U_2\)上の点を\((\cos\theta_2,\sin\theta_2)\)とすれば
\[\varphi_1:(\cos\theta_1,\sin\theta_1)\mapsto\theta_1\]
\[\varphi_2:(\cos\theta_2,\sin\theta_2)\mapsto\theta_2\]
は同相写像なので、\(S^1\)上の任意の点は開被覆\(U_1,U_2\)のどちらかに含まれ、1次元ユークリッド空間の局所座標\(\varphi_1,\varphi_2\)のいずれかに写すことができるので\(S^1\)は1次元多様体といえます。
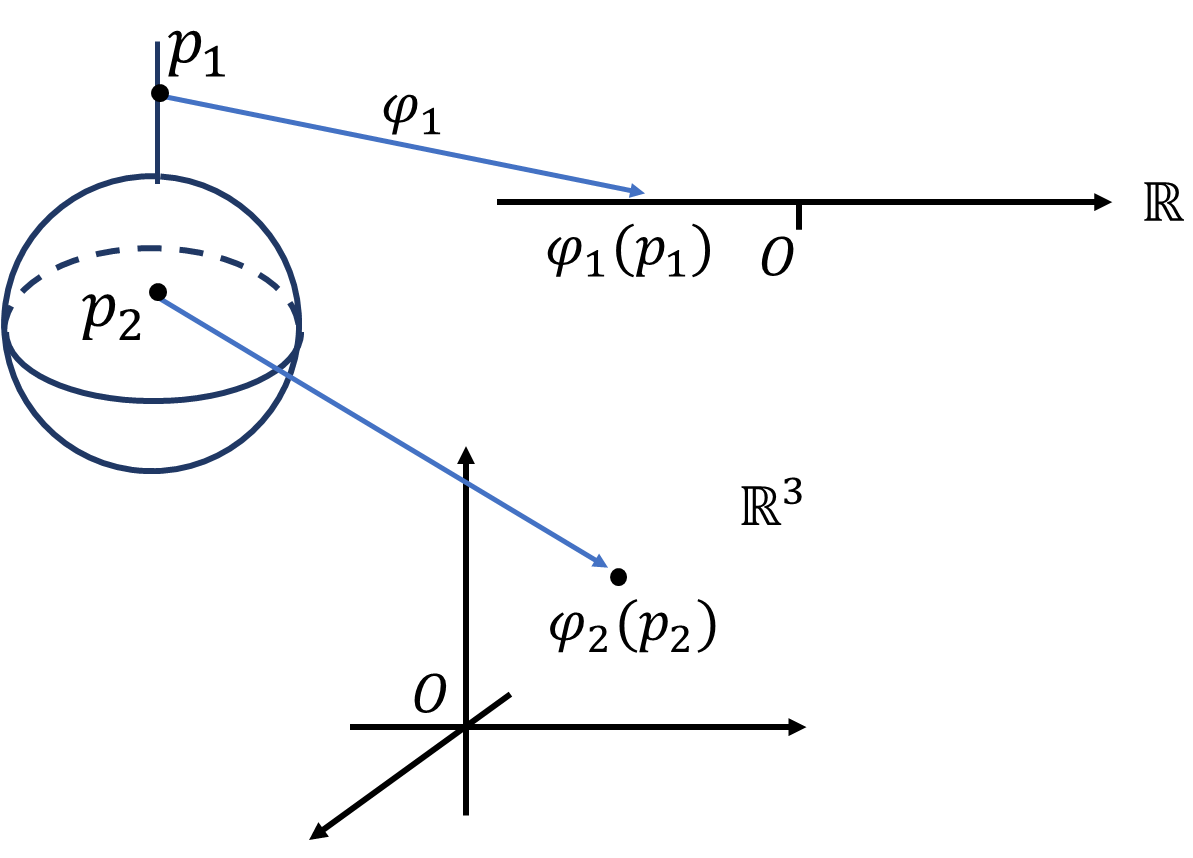
例4 楕円の周の回転体\(M\)
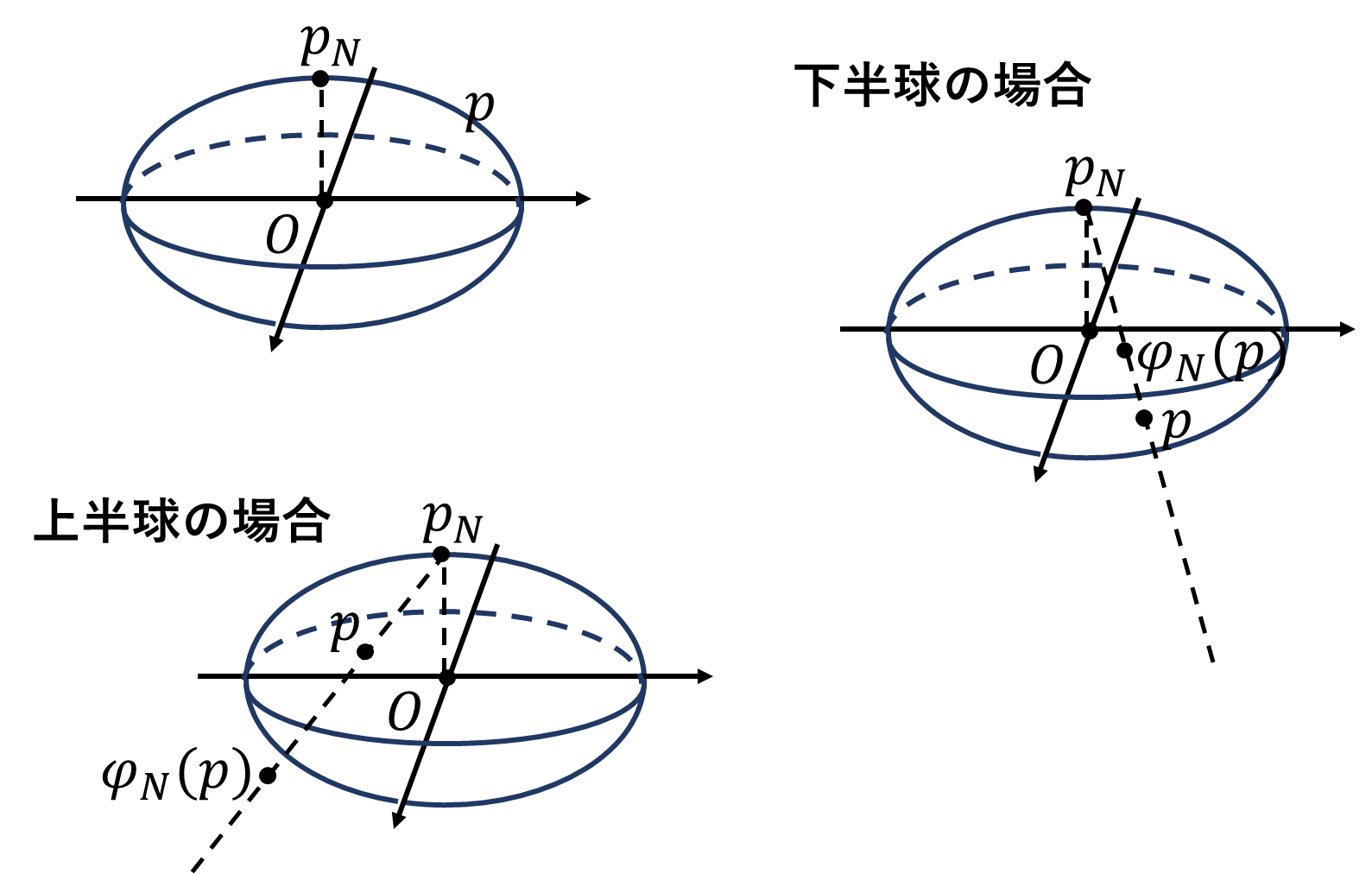
楕円の回転体に図のようにユークリッド平面\(\mathbb{R}^2\)を取ります。\(M\)の北極点を\(p_N\)、南極点を\(p_S\)とします。\(p_N\)から\(\mathbb{R}^2\)上の任意の1点\(\varphi_N(p)\)に直線を伸ばします。その時必ず直線は\(M\)上のどこかしらの1点\(p\)を貫きます。イメージしずらければ上半球と下半球で場合分けしてみると分かりやすいかもしれません。\(\varphi_N\)は\(p_N\)を除く\(M\)つまり\(M\setminus\{p_N\}\)から\(\mathbb{R}^2\)への同相写像となります。まったく同じことを\(p_S\)からもやることで、\(M\)の開被覆
\[M=M\setminus\{p_S\}\cup M\setminus\{p_N\}\]
とその局所座標
\[\varphi_N:M\setminus\{p_N\}\to\mathbb{R}^2\]
\[\varphi_S:M\setminus\{p_S\}\to\mathbb{R}^2\]
を得ます。\(M\)は
\[\mathcal{S}=\{(M\setminus\{p_N\},\varphi_N),(M\setminus\{p_S\},\varphi_S)\}\]
をアトラスとする2次元多様体です。今から(iii)座標変換について説明します。この多様体で別の開被覆を取ってみましょう。
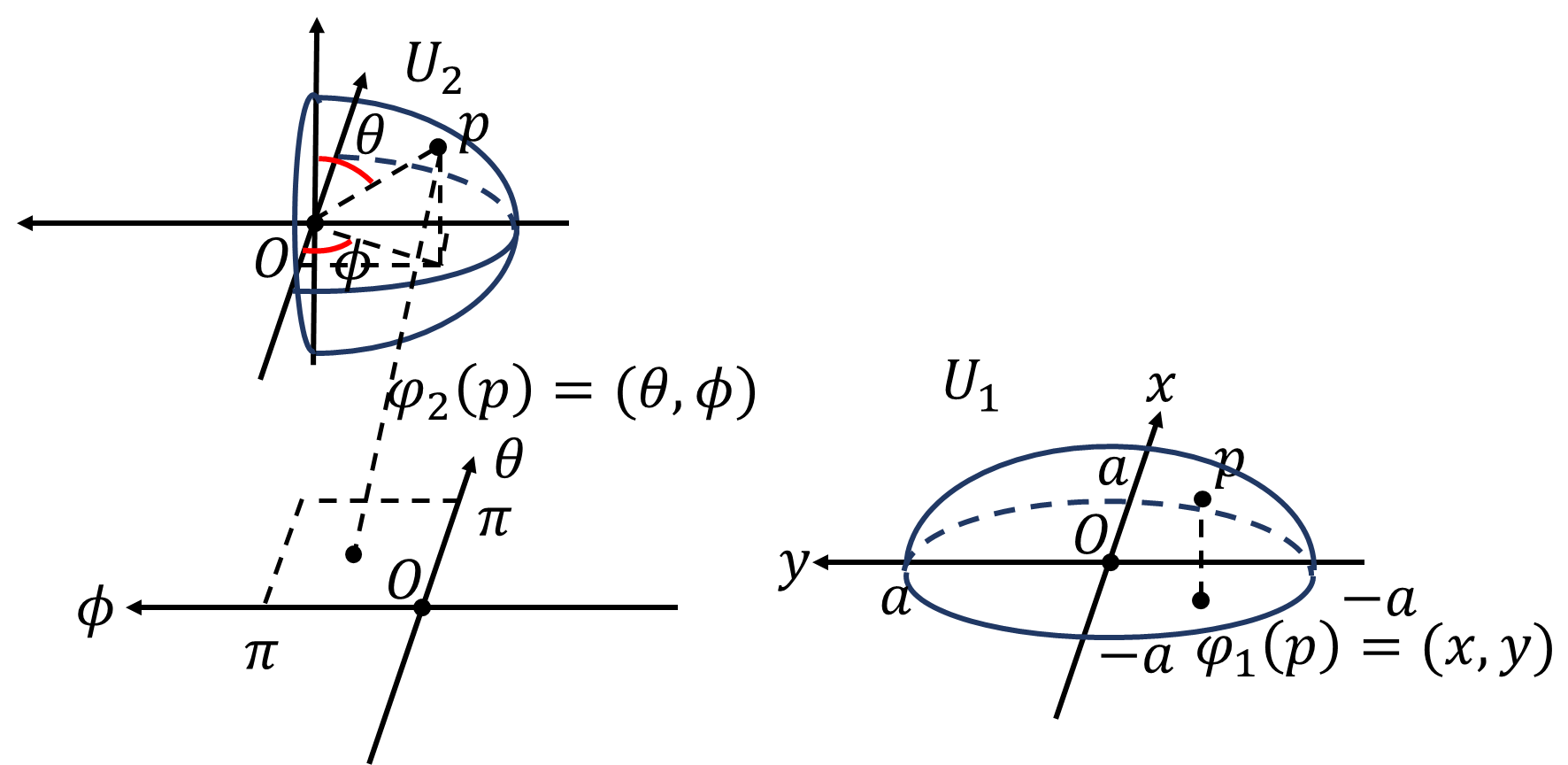
\(U_1\)を上半球、\(U_2\)を右半球(そんな言葉あるのか?)とします。これらは\(M\)の開被覆です。\(U_1\)は図のように点\(p\)を\(xy\)平面への射影\(\varphi_1\)(\(xy\)平面にまっすぐ下す写像)を取ります。\(U_2\)は\(p\)の極座標のうち\(\theta,\phi\)だけを取ってくる写像\(\varphi_2\)を取ります。
\[\varphi_1(U_1)=\{(x,y)\ |\ x^2+y^2=a^2\}\]
は\(\mathbb{R}^2\)上の境界のない円(開集合)となります。
\[\varphi_2(U_2)=\{(\theta,\phi)\ |\ 0\lt\theta\lt\pi,\ 0\lt\phi\lt\pi\}\]
は\(\mathbb{R}^2\)上の境界のない正方形(開集合)となるので、\((U_1,\varphi_1),(U_2,\varphi_2)\)はチャートです。この2つのチャートを使って座標変換をしてみます。
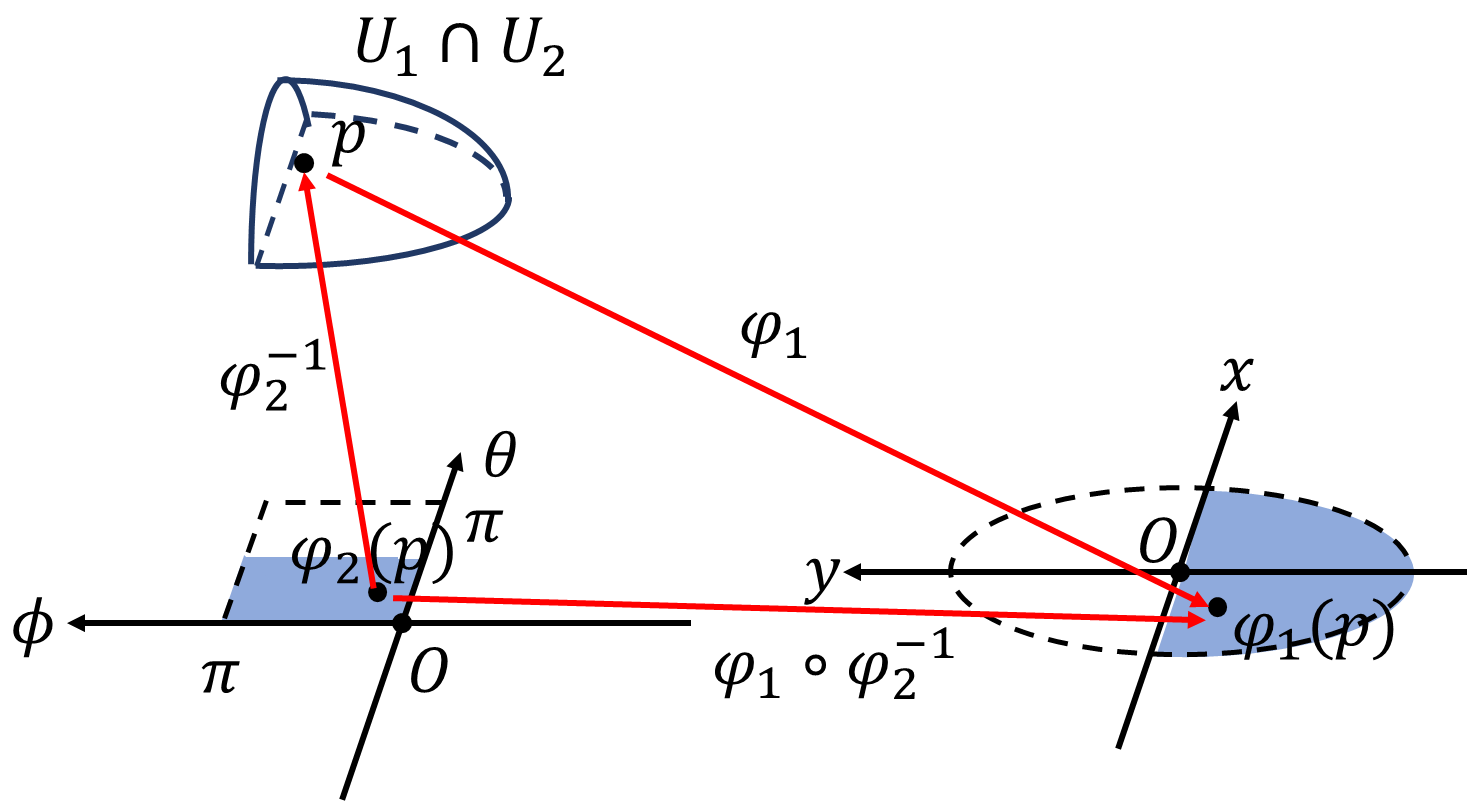
\(\varphi_1(U_1\cap U_2)\)は\(\mathbb{R}^2\)上で半円となります。\(\varphi_2(U_1\cap U_2)\)は、正方形の下半分になります。
\[\varphi_1(U_1\cap U_2)=\{(x,y)\ |\ x^2+y^2=a^2,\ 0\lt x\}\]
\[\varphi_2(U_1\cap U_2)=\left\{(\theta,\phi)\ \middle|\ 0\lt\theta\lt\frac{\pi}{2},\ 0\lt\phi\lt\pi\right\}\]
以下はこの範囲に限った話です。図から明らかですが、\((\theta,\phi)\)を\(p\)に写す写像は、\(\varphi^{-1}_2:(\theta,\phi)\mapsto p\)更に\(p\)を\((x,y)\)に写す写像は\(\varphi_1:p\mapsto(x,y)\)なので、
\[\varphi_1(\varphi_2^{-1}(\theta,\phi))=(x,y)=(a\sin\theta\cos\phi,a\sin\theta\sin\phi)\]
これを\(\varphi_1\circ\varphi_2^{-1}\)と表しているわけです。逆に\((x,y)\)を\((\theta,\phi)\)写す写像は、\(\varphi_2\circ\varphi_1^{-1}\)です。座標変換についてはこれくらいでいいでしょう。
上半空間\(H^m\)
上半空間\(H^m\)を、
\[H^m:=\{(x^1,x^2,\cdots,x^m)\ |x^m\ \ge0\}\]
で定義します。\(m\)次元ユークリッド空間で、境界を含む上半分です。その境界\(\partial H^m\)は、
\[\partial H^m:=\{(x^1,x^2,\cdots,x^{m-1})\ |x^m=0\}\]
で定義しておきます。
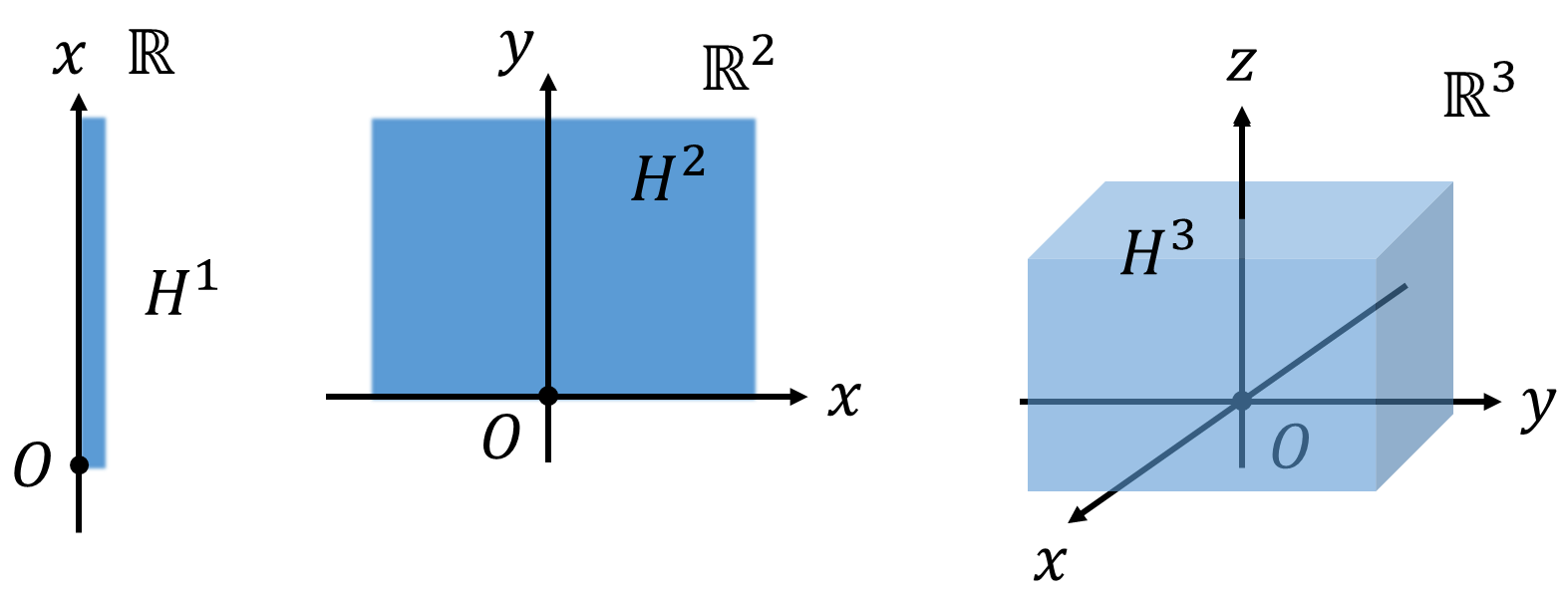
\(H^1\)であれば原点を含む正の実数全体で\(\partial H^1\)は原点\(O\)となります。\(H^2\)は、\(x\)軸上の点を含む第1象限、第2象限となります。\(\partial H^2\)は\(x\)軸です。この上半区間を使って境界のある多様体を定義していきます。\(H^3\)は3次元ユークリッド空間の\(z\ge0\)となる点全体の集合で、\(\partial H^3\)は\(xy\)平面となります。\(H^1=[0,\infty)\)は1次元ユークリッド空間\((\mathbb{R},\mathfrak{O}_{\mathbb{R}})\)では半開区間となりますが、上半空間\(H^1\)を位相空間\((H^1,\mathfrak{O}_{H^1})\)と見た場合は、位相のルール1\(X,\varnothing\in\mathfrak{O}\)より、\(H^1=[0,\infty)\in\mathfrak{O}_{H^1}\)も開集合です。また位相のルール2\(\bigcup O_\lambda\in\mathfrak{O}\)\([0,5)\cup(2,\infty)=H^1\in\mathfrak{O}_{H^1}\)なので、\([0,5)\)なども位相\(\mathfrak{O}_{H^1}\)では開集合となります。多様体\(M\)の開被覆\(U\)が境界を含んでいても開被覆と呼びますので注意しましょう。
境界付き多様体
多様体\((M,\mathcal{S})\)をどのように定義したか思い出しましょう。\(M\)をハウスドルフ空間として、開被覆\(U\)とその\(m\)次元ユークリッド空間への同相写像\(\varphi:U\to \mathbb{R}^m\)の組\((U,\varphi)\)をチャートと呼び、アトラス\(\mathcal{S}\)は\(M\)全体を覆うチャートの集合でした。よくよく考えると、\(\varphi(U)\)は開集合なので、それと同相な開被覆\(U\)も開集合となります。境界を含む開集合を扱うには\(U\)が境界をもつ空間と同相である必要があります。境界を持つ多様体を導入するために\(\varphi\)を上半空間\(H^m\)上の開集合への同相写像としてみます。いかに例をあげてみます。
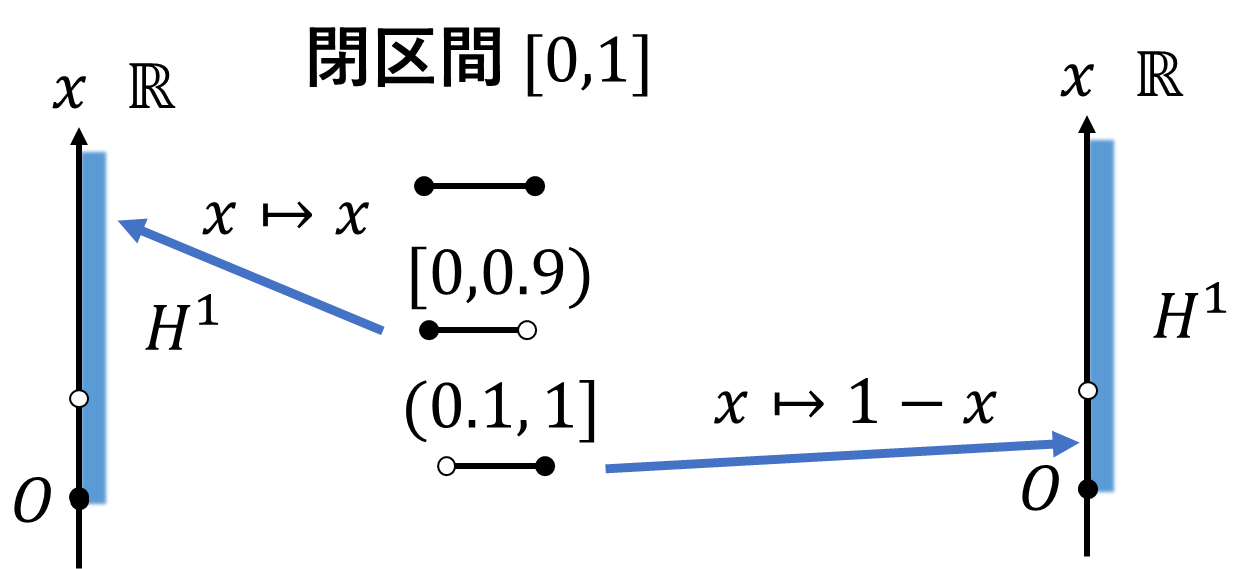
\(I=[0,1]\)閉区間は、
\[U_1=[0,0.9),\ U_2=(0.1,1]\]
という2つの開被覆で覆うことができます。
\[\varphi_1(x)=x,\ \varphi_2(x)=1-x\]
という2つの局所座標を用いることで、\([0,1]\)閉区間は\(\mathcal{S}=\{(U_i,\varphi_i)\}_{i=1}^2\)をアトラスとする境界付き多様体となります。
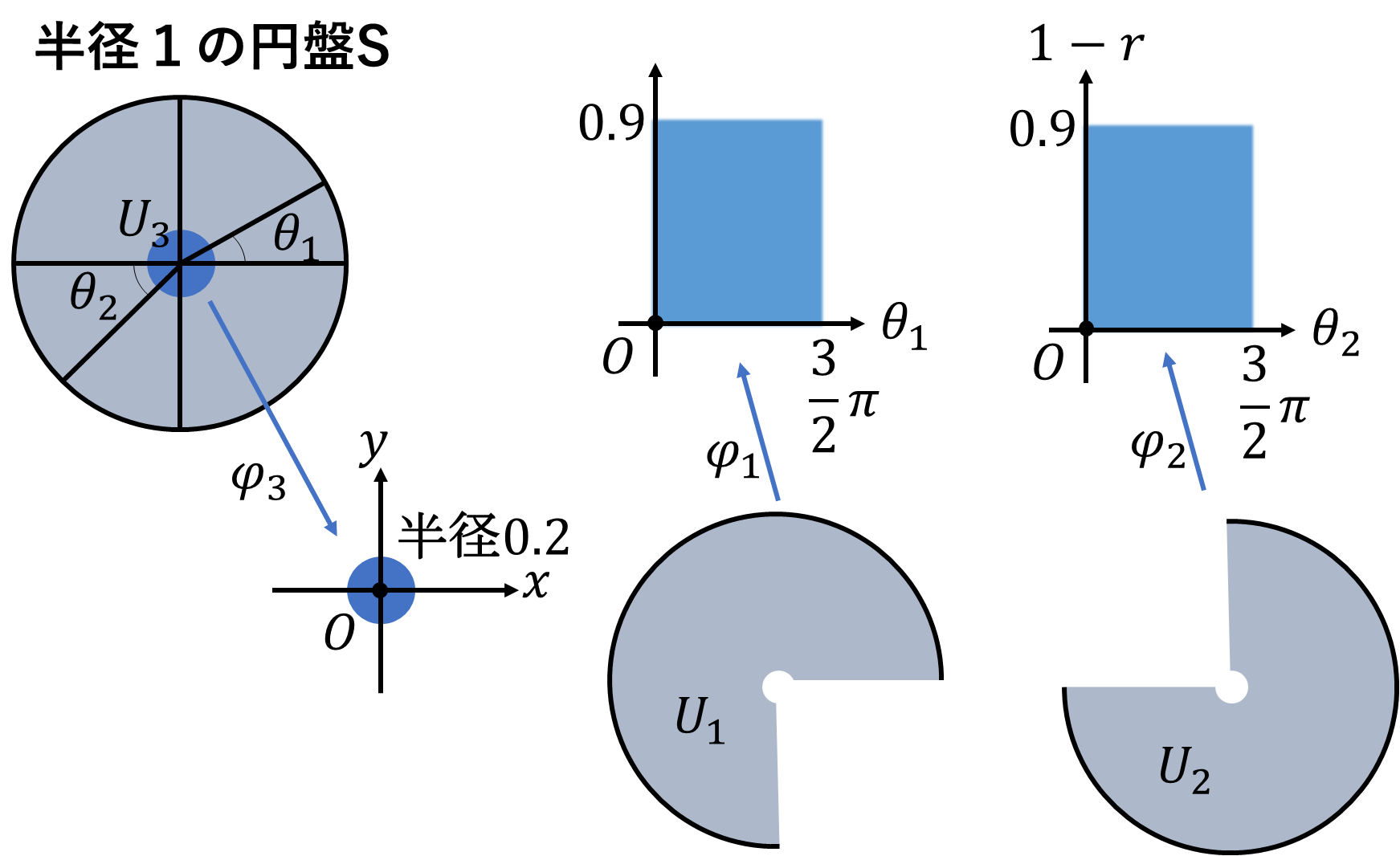
次の例は半径1の円盤\(S\)です。次のような開被覆を設定します。角度\(\theta_1,\theta_2\)を図のようにとります。\(r\)は円盤\(S\)の中心からの距離とします。円盤\(S\)から半径\(0.1\)の円盤を除いた第1から3象限の部分を\(U_1\)、第1、3、4象限を\(U_2\)とします。円盤と同じ中心を持つ半径\(0.2\)の開円盤を\(U_3\)とします。
\[S=\bigcup_{i=1}^3U_i\]
なので、\(\{U_i\}_{i=1}^3\)は\(S\)の開被覆です。\(U_3\)をそのままユークリッド平面に写す写像を\(\varphi_3\)として、
\[\varphi_1(U_1)=\left\{(r-1,\theta_1)\ \middle|\ 0.1\lt r\le1,\ 0\lt\theta_1\lt\frac{3\pi}{2}\right\}\subset H^2\]
\[\varphi_2(U_2)=\left\{(r-1,\theta_2)\ \middle|\ 0.1\lt r\le1,\ 0\lt\theta_1\lt\frac{3\pi}{2}\right\}\subset H^2\]
\[\varphi_3(U_3)=\{(x,y)\ |\ x^2+y^2=1\}\subset\mathbb{R}^2\]
円盤\(S\)は\(\mathcal{S}=\{(U_i,\varphi_i)\}_{i=1}^3\)をアトラスとして境界付き多様体となります。
多様体でない例
多様体の定義にハウスドルフ性は必要なのでしょうか?\(m\)次元ユークリッド空間\(\mathbb{R}^m\)上の任意の2点は交わらない開集合で分離できます。多様体が部分的に\(\mathbb{R}^m\)上の開集合と同相ならば多様体は自動的にハウスドルフ空間になりそうですが、そうとは限りません。

\(M\)上で原点\(O\)を含む開集合\(U\ni O\)を取ると、\(O'\)も\(U\)に含まれてしまうので、\(M\)は非ハウスドルフです。\(\mathbb{R},\mathbb{R}'\)を\(M\)の開被覆とみなせば、\(\{(\mathbb{R},\mathrm{id}),(\mathbb{R}',\mathrm{id})\}\)をアトラスとする非ハウスドルフ多様体となります。(\(\mathrm{id}:x\mapsto x\)は恒等写像)これが局所ユークリッドでかつ全体としてハウスドルフでない例です。(これはnon hausdorff manifoldというwikiのページで見つけました。)
このように球体に線分を付けた図形は多様体ではありません。\(m\)次元多様体は任意の点付近の開集合が\(m\)次元ユークリッド空間の開集合に同相でなければ、ならないためこれは1次元多様体にも3次元多様体にも分類できません。(頭部の開集合は3次元ユークリッド空間の開集合に同相、毛の部分の開集合は1次元ユークリッド空間の開集合に同相となります。)今回はここまでにします。












