楽しい科学（理論）チャンネル

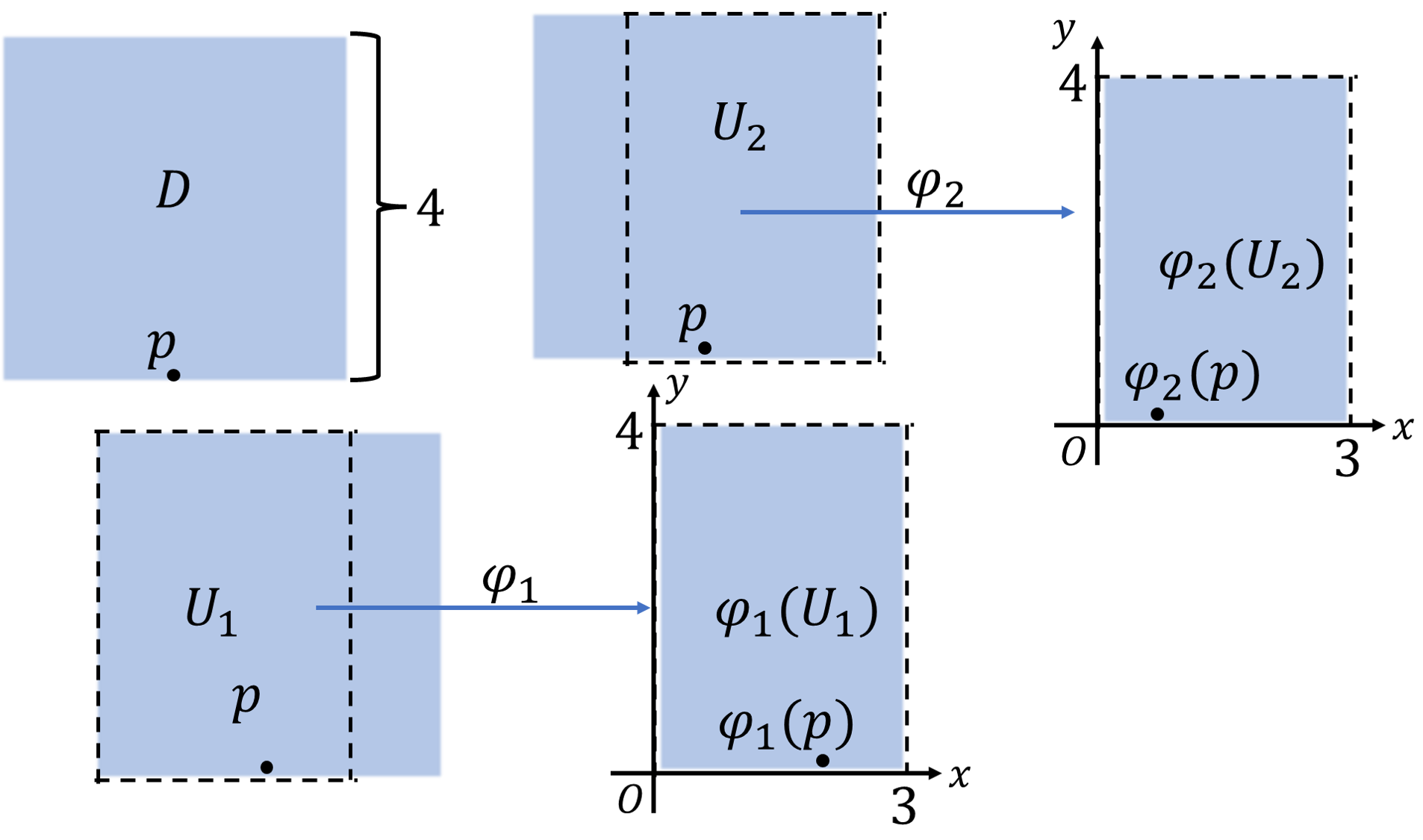
　ここで境界のない高さが４底辺が３の長方形領域\(U_1,U_2\)を取ります。これら\(U_1,U_2\)を\(D\)の開被覆とみなして２次元ユークリッド空間へのそのまま写す写像を\(\varphi_1=(x^1,x^2),\varphi_2=(y^1,y^2)\)とします。これにより、正方形\(D\)は \[\mathcal{S}=\{(U_1,\varphi_1),(U_1,\varphi_1)\}\] をアトラスとする多様体となります。開被覆\(U_1\cap U_2\)が存在するので、座標変換は、 \[\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(x^1+1,x^2)\] または、 \[\varphi_2\circ\varphi_1^{-1}(x^1,x^2)=(y^1-1,y^2)\] となります。\(C^r\)級であるとは、\(r\)回まで微分が可能であるということです。 \[\frac{\partial}{\partial x^1}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(1,0)\] \[\frac{\partial}{\partial x^2}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(0,1)\] これで１回微分可能であることが分かったので、\((D,\mathcal{S})\)は\(C^1\)級多様体です。 \[\frac{\partial}{\partial x^1\partial x^1}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(0,0)\] \[\frac{\partial}{\partial x^2\partial x^1}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(0,0)\] \[\frac{\partial}{\partial x^1\partial x^2}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(0,0)\] \[\frac{\partial}{\partial x^2\partial x^2}\varphi_1\circ\varphi_2^{-1}(y^1,y^2)=(0,0)\] 微分可能かどうかはすべてのパターンを試さなくてはなりません。ここでどこかが微分不可能だったら\(C^1\)級可微分多様体となります。2回まで微分できたので、\(C^2\)級可微分多様体となります。これ以降どのように微分してもその微分は\((0,0)\)になるので、\((D,\mathcal{S})\)は\(C^\infty\)級可微分多様体です。次の例は直線\(l\)です。

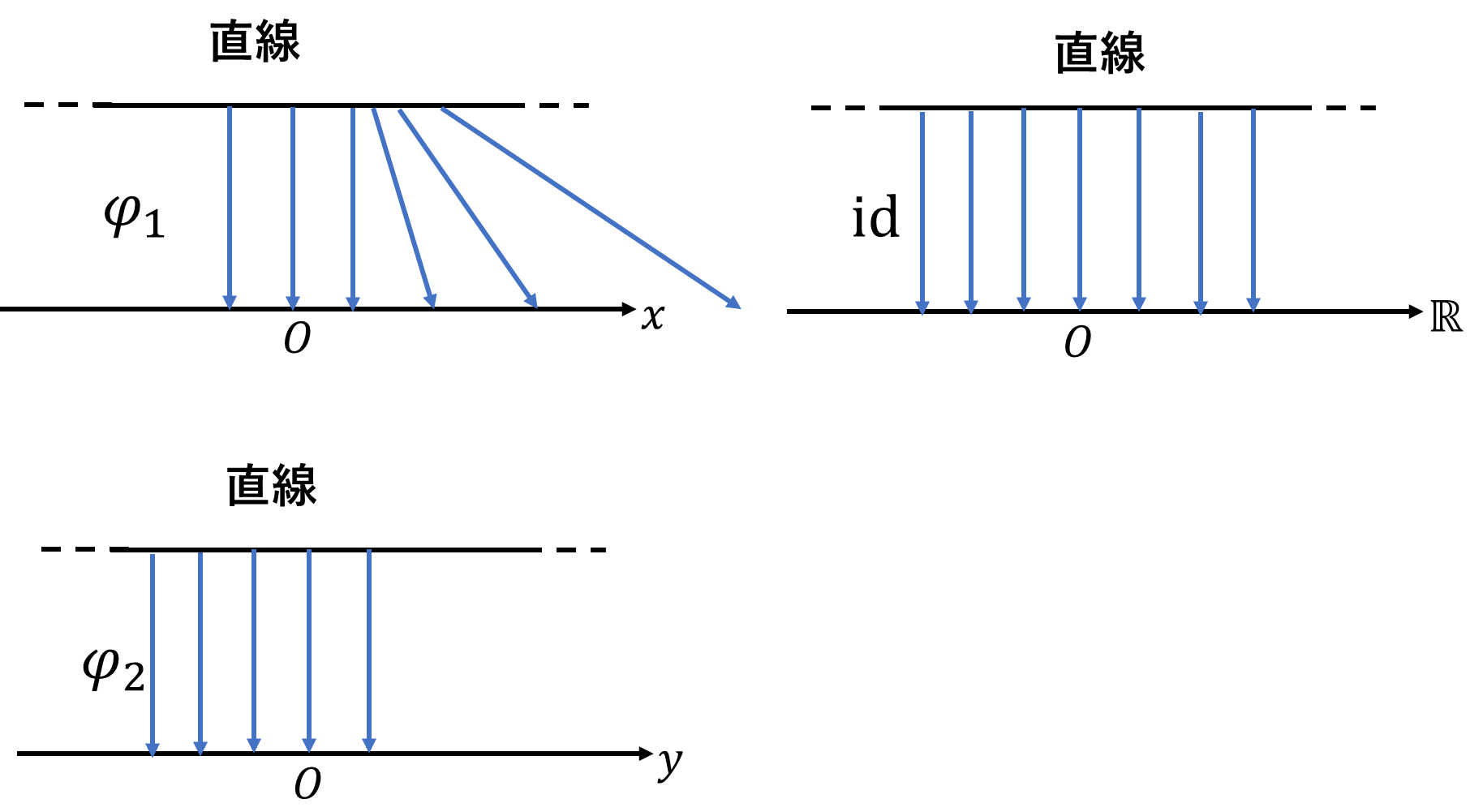
　局所座標\(\varphi_1\)は０以下では、直線から１次元ユークリッド空間にそのまま写し、０以上では２次関数のように写す写像とします。\(\varphi_2\)は直線上の点をそのまま１次元ユークリッド空間に写す写像です。数直線\(l\)に２つの開被覆\(U_1,U_2\)を\(\varphi_1(U_1)=(-1,\infty),\varphi_2(U_2)=(-\infty,1)\)となるように取ります。直線\(l\)は \[\mathcal{S}=\{(U_1,\varphi_1),(U_2,\varphi_2)\}\] をアトラスとする多様体となります。 \[\varphi_1\circ\varphi_2^{-1}(y)=x=\begin{cases}y&-1\lt y\le0 \\y^2&0\le y\lt1\end{cases}\] では\(y=0\)で左極限と右極限で微分係数を見ていきます。 \[\lim_{h\to-0}\frac{\varphi_2\circ\varphi_1^{-1}(0+h)-\varphi_2\circ\varphi_1^{-1}(0)}{h}\] \[=\lim_{h\to-0}\frac{0+h-0}{h}=1\] 次に右極限葉となります。 \[\lim_{h\to+0}\frac{\varphi_2\circ\varphi_1^{-1}(0+h)-\varphi_2\circ\varphi_1^{-1}(0)}{h}\] \[=\lim_{h\to+0}\frac{(0+h)^2-0^2}{h}=0\] \(\varphi_2\circ\varphi_1^{-1}\)は微分できないので\((l,\mathcal{S})\)は\(C^0\)級多様体です。連続多様体などと呼ばれます。次に直線\(l\)に \[\mathcal{T}=\{(U_1,\varphi_2),(U_2,\varphi_2)\}\] というアトラスを取ります。どちらのチャートも\(l\)上の点をそのまま１次元ユークリッド空間に写す写像となります。座標変換は、 \[\varphi_2\circ\varphi_2(y)=x=y\] なので、座標変換は微分可能で、 \[\frac{d}{dy}\varphi_2\circ\varphi_2(y)=1,\ \frac{d^r}{dy^r}\varphi_2\circ\varphi_2(y)=0\] 一度微分するとあとはずっと０なので、\((l,\mathcal{T})\)は\(C^\infty\)級可微分多様体です。 多様体\((M,\mathcal{S})\)が可微分多様体かどうかは、アトラス\(\mathcal{S}\)に依ります。ちなみに１つのチャートで表せる多様体は、\(C^\infty\)級か微分多様体となります。\((U,\varphi)\)しかないので、 \[\varphi\circ\varphi^{-1}(x^1,x^2,\cdots,x^m)=(x^1,x^2,\cdots,x^m)\] \[\frac{\partial}{\partial x^1}\varphi\circ\varphi^{-1}(x^1,x^2,\cdots,x^m)=(1,0,\cdots,0)\] 他の成分も同様に座標変換の微分ができるので可微分多様体となります。つまり境界のない球、境界のない直方体はそれ自体を開被覆として３次元ユークリッド空間への自身を写す局所座標を取れば可微分多様体ですし、境界のない正方形や厚みのない境界のない円盤はそれ自身を開被覆として２次元ユークリッド空間にそのまま写す写像を取れば可微分多様体になります。今までの例は全て１つのチャートでアトラスを構成できる多様体を見てきました。次は円周\(S^1\)です。

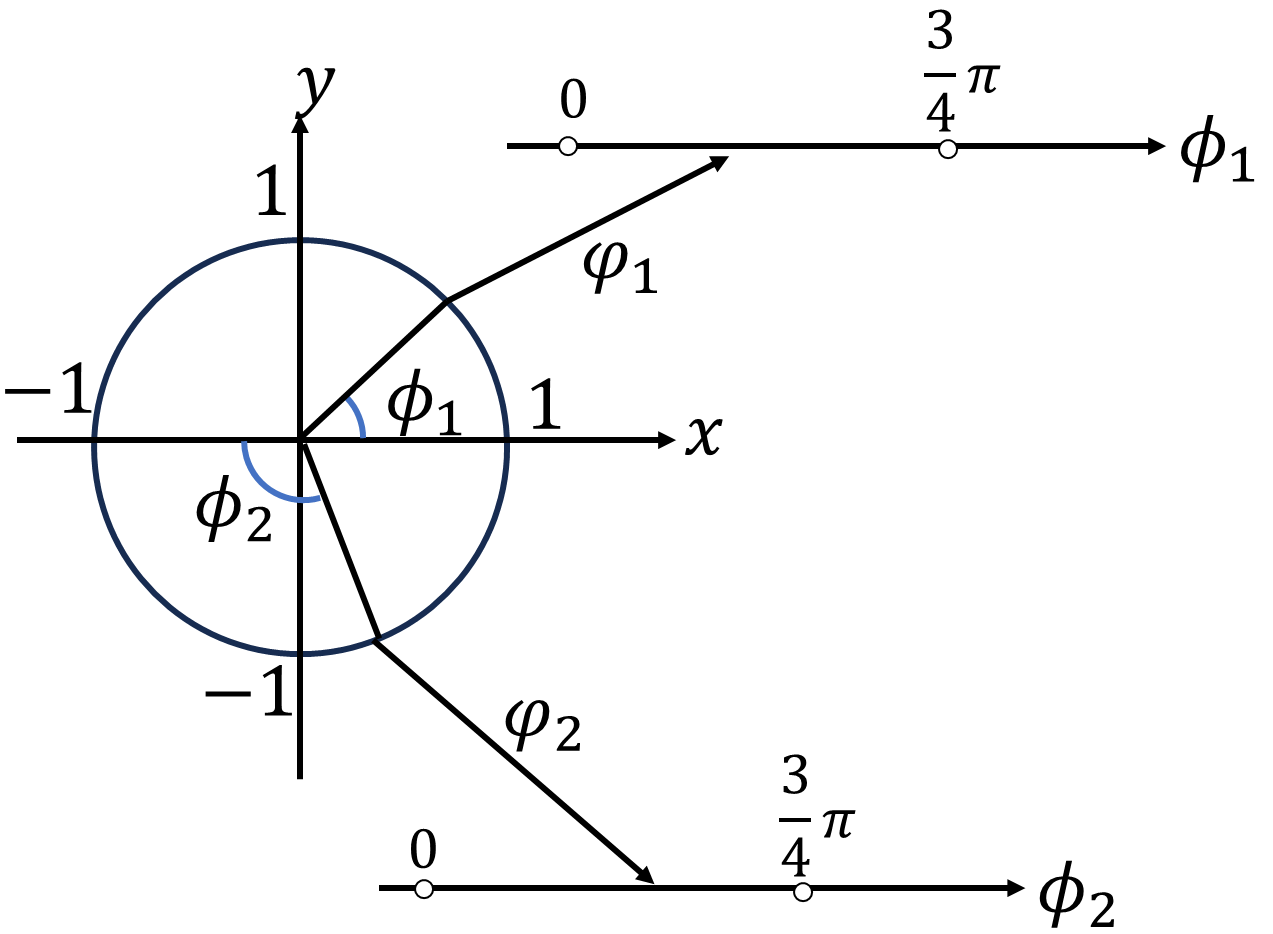
　多様体には座標系は備わっていないのですが、写像の説明がしずらいので今回は座標を付けて見ました。\(x\)軸正から反時計回りに角度\(\phi_1\)、\(x\)軸負から反時計回りに角度\(\phi_2\)を取ります。\(S^1\)を開被覆で覆いつくすには少なくとも２つの開被覆が必要で、 \[U_1=\left\{(\cos\phi_1,\sin\phi_1)\ \middle|\ 0\lt\phi_1\lt\frac{3\pi}{2}\right\}\] \[U_2=\left\{(\cos\phi_2,\sin\phi_2)\ \middle|\ 0\lt\phi_2\lt\frac{3\pi}{2}\right\}\] 局所座標を \[\varphi_1:(\cos\phi_1,\sin\phi_1)\to\phi_1\] \[\varphi_1:(\cos\phi_1,\sin\phi_1)\to\phi_2\] このように取れば円周\(S^1\)は\(\mathcal{S}=\{(U_1,\varphi_1),(U_2,\varphi_2)\}\)をアトラスとする多様体となります。\(U_1\cap U_2\)での座標変換は、 \[\varphi_2\circ\varphi_1^{-1}(\phi_1)=\phi_2=\begin{cases}\phi_1-\pi&(0\lt\phi_1\lt\frac{\pi}{2}) \\\phi_1+\pi&(\pi\lt\phi_1\lt\frac{3\pi}{2})\end{cases}\] 座標変換を微分してみると、 \[\frac{d}{d\phi_1}\varphi_2\circ\varphi_1^{-1}(\phi_1)=1,\ \frac{d^r}{d\phi_1^r}\varphi_2\circ\varphi_1^{-1}(\phi_1)=0\] よって\((S^1,\mathcal{S})\)は\(C^\infty\)級可微分多様体となります。これも直線の時にようにアトラスによっては可微分多様体にならないこともあります。

多様体上の関数

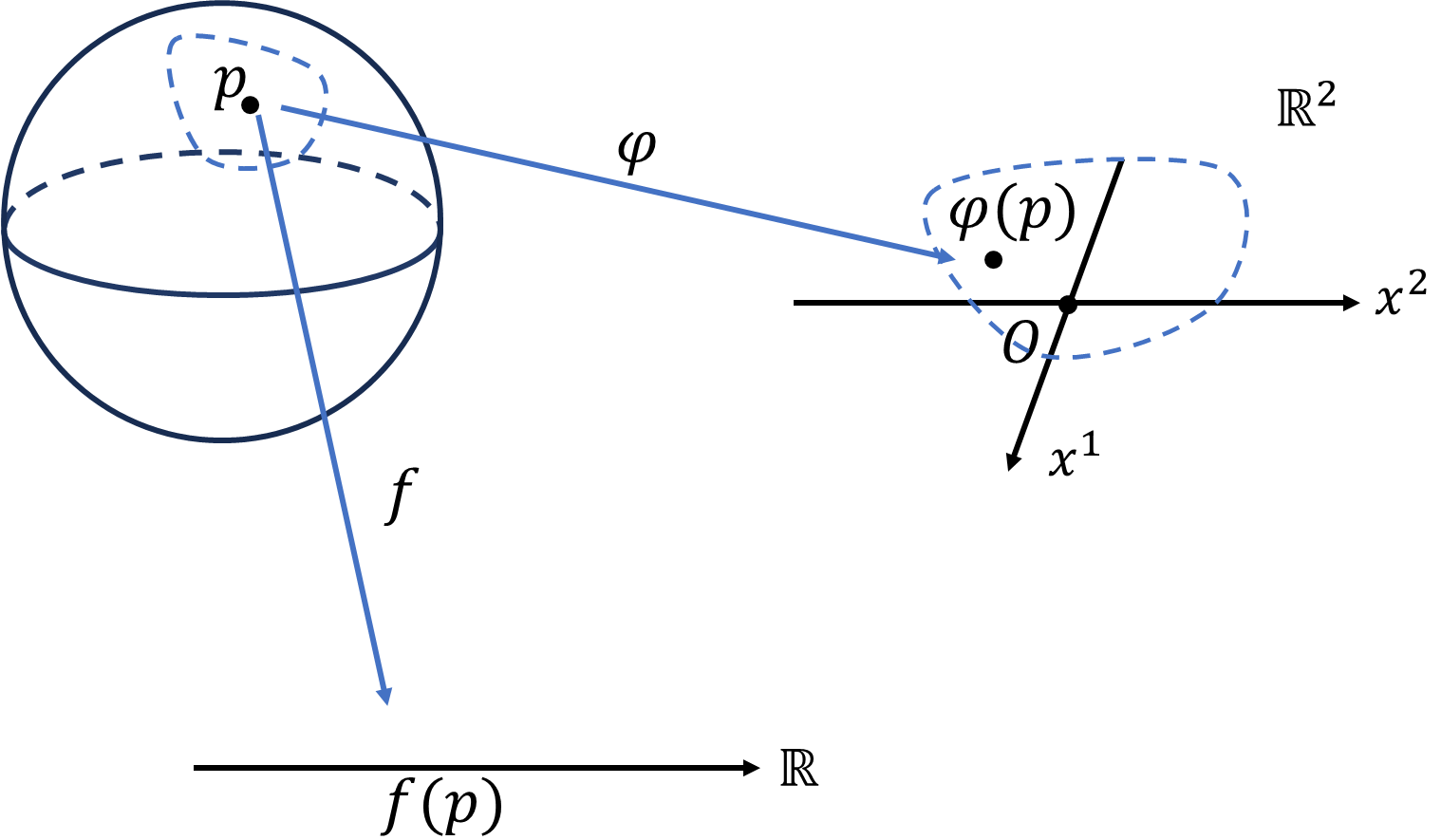
　地球の表面\(S^2\)を多様体とみなした時、地球表面の温度\(T(p)\)や、海面からの高さ標高\(h(p)\)などは多様体\(S^2\)上の関数です。この場合チャート\((U,\varphi)\)はある地域の地図などが該当します。多様体に備え付けの座標はありませんが、局所座標\(\varphi_1(p)=(x^1,x^2)\)を用いて、 \[f(p)=f(\varphi^{-1}_1(x^1,x^2))=f\circ\varphi^{-1}_1(x^1,x^2)\] 多様体上の関数は局所座標を使って表すことができます。\(U_2\ni p\)をみたす別の開被覆があったとして、同じスカラー値\(f(p)\)を別のチャート\((U_2,\varphi_2)\) \[f(p)=f(\varphi^{-1}_2(y^1,y^2))=f\circ\varphi^{-1}_2(y^1,y^2)\] で表すことができます。地球の表面上のある点\(p\)をどのような座標で表そうが、温度、標高は、座標ではなく点\(p\)に依存する値ということです。例えば\(\mathbb{R}^3\)上の直交座標系での万有引力ポテンシャルエネルギー\(U\)を \[U(x,y,z):=-\frac{GMm}{\sqrt{x^2+y^2+z^2}}\] などと定義しますが、多様体上に座標が入っているわけではないので、多様体上で関数\(U(p)\)を具体的に書くために座標\(\varphi_1:p\mapsto(x_p,y_p,z_p)\)が必要で、 \[U(p)=U(\varphi_1^{-1}(\varphi_1(p)))=U\circ\varphi_1^{-1}(\varphi_1(p))=U\circ\varphi_1^{-1}(x,y,z)\] \[U(p)=U\circ\varphi_1^{-1}(x,y,z)=-\frac{GMm}{\sqrt{x^2+y^2+z^2}}\] と表してあげなくてはなりません。また適切な開被覆の共通部分(例えば\(x,y,z\gt0\)の部分に限定するなど)で、例えば局所座標\(\varphi:p\mapsto(r,\theta,\phi)\)について座標変換が、 \[\varphi_2\circ\varphi_1^{-1}(x,y,z)=(r,\theta,\phi)=\left(\sqrt{x^2+y^2+z^2},\arctan\frac{\sqrt{x^2+y^2}}{z},\arctan\frac{y}{x}\right)\] と表せるなら、万有引力ポテンシャルエネルギーは \[U(p)=U\circ\varphi_2^{-1}(r,\theta,\phi)=-\frac{GMm}{r}\] とも表すことができて\(U(p)\)は局所座標の取り方に依って見た目は変わりますが、その値が変わらないと言っているだけです。

多様体上の関数の微分

　次に多様体上の関数の微分を見てみます。微分も局所座標を用いて表します。今は簡単に複数のチャートで構成されたアトラスを持つ２次元多様体\(M\)を考えます。あるチャート\((U_1,\varphi_1)=(U_1(x^1,x^2))\)で、多様体上の関数の微分は、 \[\frac{\partial}{\partial x^1}f\circ\varphi_1^{-1}(x^1,x^2)\] しかしこの微分は、多様体\(M\)上の\(U_1\)でしか成り立たない点には注意が必要です。さらに\(U_1\cap U_2\neq\varnothing\)であるチャート\((U_2,\varphi_2)=(U_2,(y^1,y^2))\)への座標変換が\(C^1\)級であれば\(\varphi_1^{-1}(x^1,x^2)=p=\varphi_2^{-1}(y^1,y^2)\)なので、 \[\frac{\partial}{\partial x^1(y_1,y_2)}f\circ\varphi_2^{-1}(y^1,y^2)\] \[=\frac{\partial y^1}{\partial x^1}\frac{\partial}{\partial y^1}f\circ\varphi_2^{-1}(y^1,y^2)+\frac{\partial y^2}{\partial x^1}\frac{\partial}{\partial y^2}f\circ\varphi_2^{-1}(y^1,y^2)\] \(U_1\cap U_2\)の範囲で、\(U_2,\varphi_2\)への微分へ変えることもできます。この性質を満たすために座標変換の微分可能回数は関数\(f\)の微分可能回数以上出なければなりません。これ以降チャートの座標変換を考える際は、必要な回数微分できるなめらかな座標変換がなされているとします。