楽しい科学（理論）チャンネル

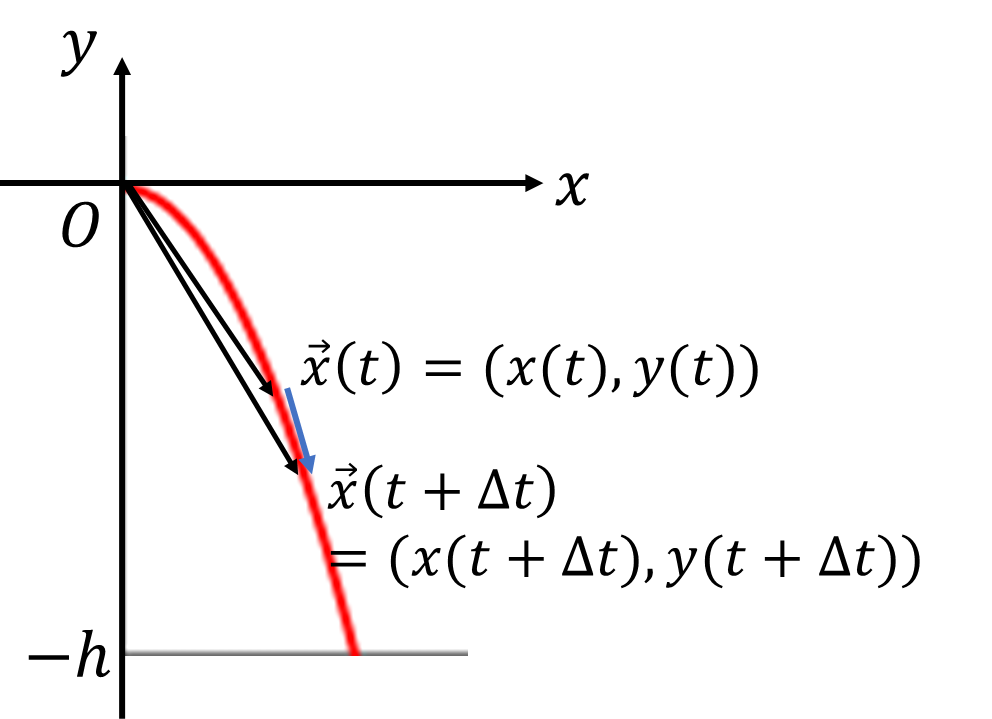
いつもの曲線です。 \[C(t)=\left\{(x,y)\ \middle|\ x=t,\ y=-\frac{1}{2}gt^2,\ 0\le t\le\sqrt{h}\right\}\] この曲線の接ベクトルを求めるもっとも簡単な方法は位置ベクトルの微分を考えることです。曲線上の位置ベクトル\(\vec{x}(t)\)を用いて、 \[\varDelta \vec{x}=\vec{x}(t+\varDelta t)-\vec{x}(t+\varDelta t):=(x(t+\varDelta t)-x(t),y(t+\varDelta t)-y(t))\] 変化量ベクトル\(\varDelta \vec{x}\)を定義します。\(\varDelta t\)を小さくし続ければ、曲線と平行になってい来ますが、その極限はゼロベクトル\(\boldsymbol{0}\)になってしまうので、これを\(\varDelta t\)で割って極限を取ります。 \[\vec{v}=\frac{d\vec{x}}{dt}:=\lim_{\varDelta t\to 0}\frac{\varDelta\vec{x}}{\varDelta t}=\left(\frac{dx}{dt},\frac{dy}{dt}\right)=(1,-gt)\] これは接ベクトルの１つで、速度ベクトルともいいます。\(\xi=t^2\)となるパラメータを取ることでも同じ曲線 \[C'(\xi)=\left\{(x,y)\ \middle|\ x=\sqrt\xi,\ y=-\frac{1}{2}g\xi,\ 0\le t\le h\right\}\] の接ベクトルを同様に微分で求めると、 \[\vec{v}'=\frac{d\vec{x}}{d\xi}:=\lim_{\varDelta t\to 0}\frac{\varDelta\vec{x}}{\varDelta \xi}=\left(\frac{dx}{d\xi},\frac{dy}{d\xi}\right)=\left(\frac{1}{2\sqrt{\xi}},-\frac{1}{2}g\right)\] よくよく見ると、\(\vec{v}\)は、\(\vec{v}'\)の\(t\)倍となっています。接ベクトルの定数倍も接ベクトルということですね。

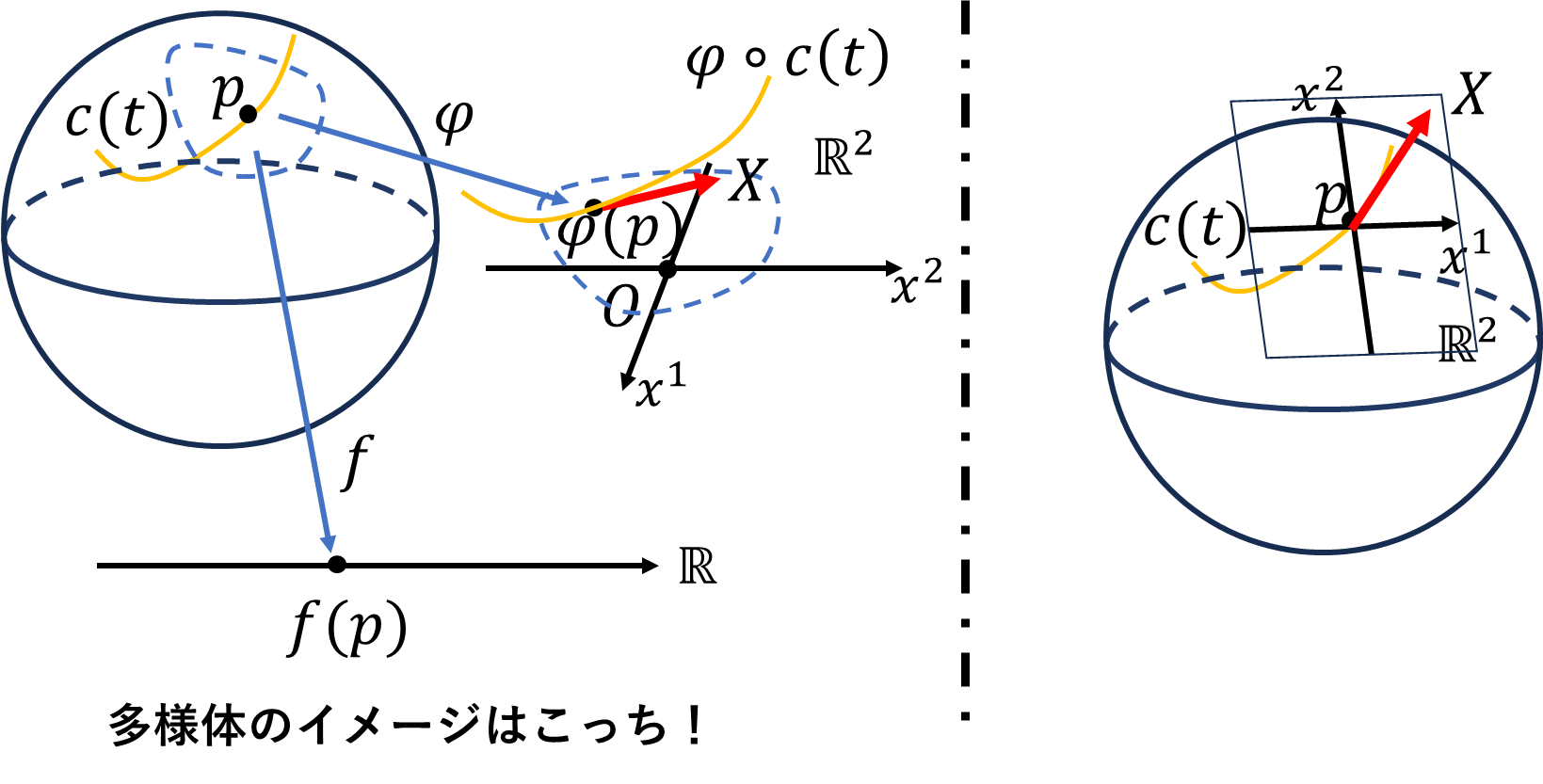
　\(\mathbb{R}^2\)上の曲線\(C(t)\)の接ベクトル\(\vec{v}\)は\(\mathbb{R}^2\)からはみ出しませんでしたが、球面\(S^2\)上の曲線\(c(t)\)をイメージしてください。曲線\(c(t)\)の接ベクトル\(X_p\)は球面からはみ出します。このベクトルの向きと大きさを測るために球面\(S^2\)との接点\(p\)に座標付きの接平面を貼るもしくは、球面を３次元空間に埋め込むなどの工夫が必要になってしまいます。多様体にはハウスドルフの分離公理を満たす位相空間\(M\)とアトラス\(\mathcal{S}\)があるだけです。多様体には外の空間や接面などの構造が供えられていません。そこで多様体上の曲線\(c(t)\)の点\(p=c(t_p)\)における接ベクトル\(X_p\)を \[X_p(\Box):=\left.\frac{d}{dt}\right|_{t=t_p}\Box\circ c(t)\] と定義します。\(\Box\)には多様体上の関数が入ります。曲線\(c\)におけるというのが大切です。曲線\(c\)によってどのような接ベクトル\(X_p\)になるかが決定するからです。この記号は\(t\)で微分した後に\(t=t_p\)を代入してくださいという意味の記号です。接ベクトルを微分演算子として定義することで局所座標に依らない定義になっています。ただこれではベクトルなのかよくわかりません。微分演算子で定義されているなら関数を作用させてみたくなります。多様体上の関数\(f:M\to\mathbb{R}\)にベクトル場を作用させてみますが、関数\(f\)の定義域を曲線\(c\)上に縛ります。つまり\(f:c(t)\to\mathbb{R}\)です。意外と複雑なことをやっていると思うので途中式を丁寧に書いていきます。 \[X_p(f)=\left.\frac{df(c(t))}{dt}\right|_{t=t_p}=\left.\frac{df\circ c(t)}{dt}\right|_{t=t_p}\] 球面上の点\(p\)を含む任意の局所座標\(\varphi=(x^1,x^2)\)を用いてより具体的に\(X_p(f)\)を記述してみます。 \[X_p(f)=\left.\frac{df(\varphi^{-1}(\varphi(c(t))))}{dt}\right|_{t=t_p}=\left.\frac{df\circ\varphi^{-1}(\varphi(c(t)))}{dt}\right|_{t=t_p}\] 曲線\(c(t)\)も局所座標に写されて、\(\varphi(c(t))=(x^1(t),x^2(t))\)と表されることにします。ここで合成関数の微分を使います。 \[X_p(f)=\left.\frac{df\circ\varphi^{-1}(x^1(t),x^2(t))}{dt}\right|_{t=t_p}\] \[=\left.\left(\frac{dx^1(t)}{dt}\frac{\partial f\circ\varphi^{-1}(x^1(t),x^2(t))}{\partial x^1}+\frac{dx^2(t)}{dt}\frac{\partial f\circ\varphi^{-1}(x^1(t),x^2(t))}{\partial x^2}\right)\right|_{t=t_p}\] \(\frac{dx^1(t)}{dt},\frac{dx^2(t)}{dt}\)にだけ\(t=t_p\)を代入して、\((\frac{dx^1(t_p)}{dt},\frac{dx^2(t_p)}{dt})=(X^1_p,X^2_p)\)と表すことにします。\(X^1_p,X^2_p\)は定数です。 \[X_p(f)=\left.\left(X^1_p\frac{\partial f\circ\varphi^{-1}(x^1(t),x^2(t))}{\partial x^1}+X^2_p\frac{\partial f\circ\varphi^{-1}(x^1(t),x^2(t))}{\partial x^2}\right)\right|_{t=t_p}\] \[X_p(f)=\left(X^1_p\left.\frac{\partial}{\partial x^1}\right|_{t=t_p}+X^2_p\left.\frac{\partial}{\partial x^2}\right|_{t=t_p}\right)f\circ\varphi^{-1}(x^1(t),x^2(t))\] \[X_p(f)=\left(X^1_p\left.\frac{\partial}{\partial x^1}\right|_{t=t_p}+X^2_p\left.\frac{\partial}{\partial x^2}\right|_{t=t_p}\right)f\circ\varphi^{-1}(\varphi(c(t)))\] \[X_p(f)=\left(X^1_p\left.\frac{\partial}{\partial x^1}\right|_{t=t_p}+X^2_p\left.\frac{\partial}{\partial x^2}\right|_{t=t_p}\right)f\circ c(t)\] ちょっと丁寧に計算しましたが、関数\(f\)はなんでも良かったのでいったん避けます。 \[X_p=X^1_p\left.\frac{\partial}{\partial x^1}\right|_{t=t_p}+X^2_p\left.\frac{\partial}{\partial x^2}\right|_{t=t_p}\] これをベクトルだと思うことにします。以下のように書いている教本が多いです。 \[X_p=X^1_p\left(\frac{\partial}{\partial x^1}\right)_p+X^2_p\left(\frac{\partial}{\partial x^2}\right)_p\] 偏微分の記号が基底で、\(X_p^i\)が成分です。別の曲線\(\gamma(\xi)\)について点\(p=\gamma(\xi_p)\)接ベクトル \[X'_p=\left.\frac{d}{d\xi}\right|_{\xi=\xi_0}\] をさっきと同じ局所座標\(\varphi=(x^1,x^2)\)を使って求めてみます。曲線\(\gamma(\xi)\)は局所座標で、\(\varphi(\gamma(\xi))=(x^1(\xi),x^2(\xi))\)と表されることにして、合成関数の微分を使って、 \[X'_p=\frac{dx^1(\xi_p)}{d\xi}\left.\frac{\partial}{\partial x^1}\right|_{\xi=\xi_p}+\frac{dx^2(\xi_p)}{d\xi}\left.\frac{\partial}{\partial x^2}\right|_{\xi=\xi_p}\] 定数の部分を\(X'^1_p,X'^2_p\)とします。 \[X'_p=X'^1_p\left.\frac{\partial}{\partial x^1}\right|_{\xi=\xi_p}+X'^2_p\left.\frac{\partial}{\partial x^2}\right|_{\xi=\xi_p}\] \((x^1(t_p),x^2(t_p))=\varphi(p)=(x^1(\xi_p),x^2(\xi_p))\)はすべて同様の点なので、接ベクトル\(X_p\)と同様の基底で表していることになります。 \[\left.\frac{\partial}{\partial x^i(t)}\right|_{t=t_p}=\left(\frac{\partial}{\partial x^i}\right)_p=\left.\frac{\partial}{\partial x^i(\xi)}\right|_{\xi=\xi_p}\] ですので、曲線の取り方によって局所座標\(\varphi\)に様々な基底ベクトルを取ることができます。定数\(a,b\)を用いて、 \[X_p=a\left(\frac{\partial}{\partial x^1}\right)_p+b\left(\frac{\partial}{\partial x^2}\right)_p\] で表されるベクトルは全て点\(p\)の接ベクトルです。多様体\(M\)の点\(p\)における接ベクトル全体の集合を接空間\(T_pM\)と言います。 \[T_pM:=\left\{a\left(\frac{\partial}{\partial x^1}\right)_p+b\left(\frac{\partial}{\partial x^2}\right)_p\ \middle|\ a,b\in\mathbb{R}\right\}\] 偏微分の記号を基底とみなせば、 \[X_p+X'_p=(X^1_p+X'^1_p)\left(\frac{\partial}{\partial x^1}\right)_p+(X^2_p+X'^2_p)\left(\frac{\partial}{\partial x^2}\right)_p\in T_pM\] 成分ごとに足し算できますし、定数\(k\)倍しても \[kX_p=kX^1_p\left(\frac{\partial}{\partial x^1}\right)_p+kX^2_p\left(\frac{\partial}{\partial x^2}\right)_p\in T_pM\] 接ベクトルになるので、ベクトルとして問題なく使えます。偏微分で表した基底がとても優秀です。

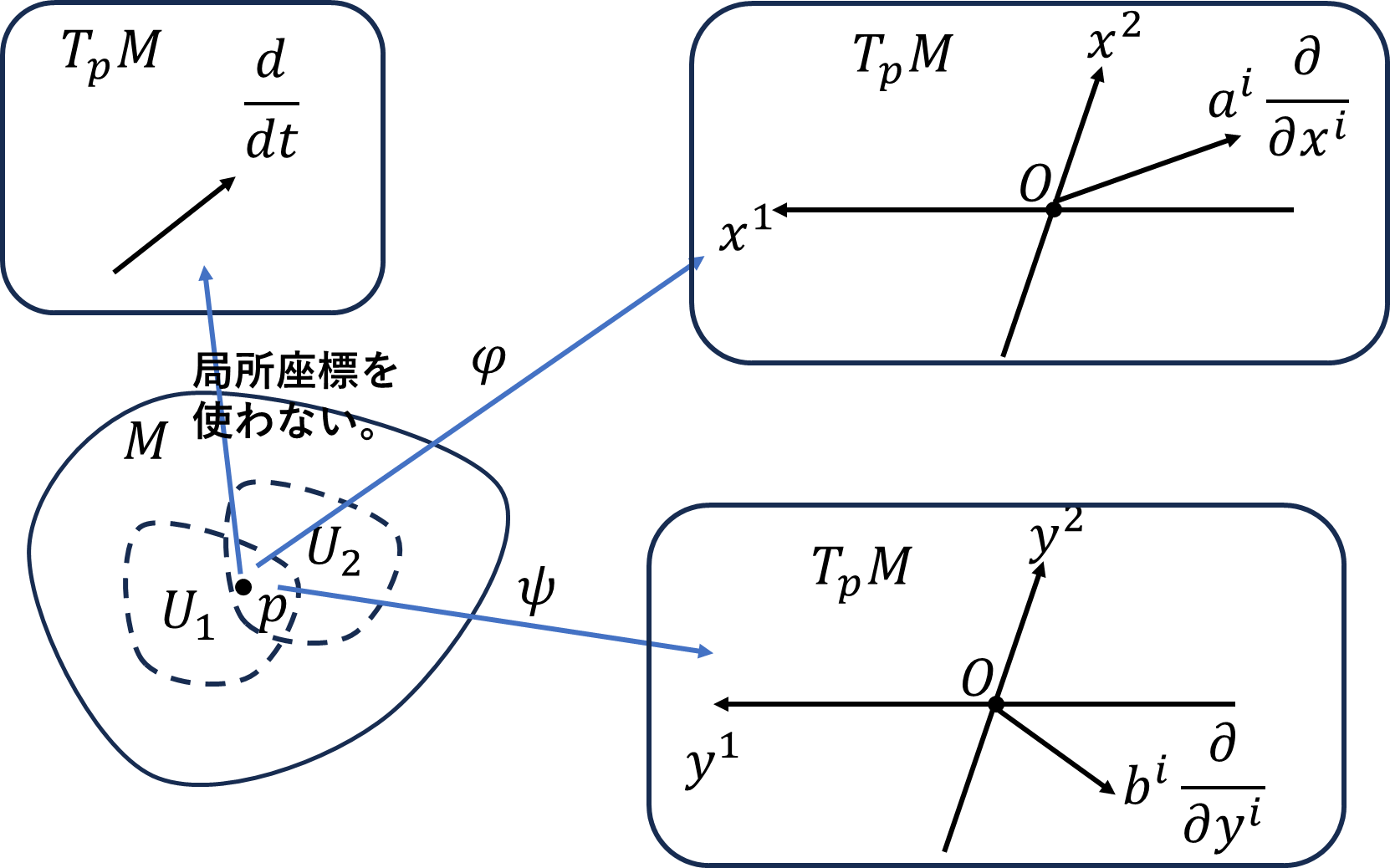
多様体上の点\(p\)が２つのチャート\(\varphi_1(U_1)=(x^1,\cdots,x^m),\varphi_2(U_2)=(y^1,\cdots,y^m)\)に含まれる場合、接ベクトル\(X_p\)は、 \[X_p=\left.\frac{d}{dt}\right|_{t=t_p}=\sum_{i=1}^ma^i\left(\frac{\partial}{\partial x^i}\right)_p\] \[X_p=\left.\frac{d}{dt}\right|_{t=t_p}=\sum_{j=1}^mb^j\left(\frac{\partial}{\partial y^j}\right)_p\] と２つの表記ができます。 \[\left(\frac{\partial}{\partial y^j}\right)_p=\sum_{i=1}^m\left.\frac{\partial x^i(t)}{\partial y^j(t)}\right|_{t=t_p}\left(\frac{\partial}{\partial x^i}\right)_p\] 偏微分の記号にチェーンルールを使います。 \[\sum_{i=1}^ma^i\left(\frac{\partial}{\partial x^i}\right)_p=\left.\frac{d}{dt}\right|_{t=t_p}=\sum_{j=1}^mb^j\left(\frac{\partial}{\partial y^j}\right)_p\] この等式を維持するために接ベクトル\(X_p\)の成分の座標変換は、 \[b^j=\sum_{i=1}^m\left.\frac{\partial y^j(t)}{\partial x^i(t)}\right|_{t=t_p}a^i\] と決まってしまいます。ここでベクトルの１次変換を思い出しましょう。 \[X'^j=\sum_{i=1}^m\frac{\partial x'^j}{\partial x^i}X^i,\ e'_j=\sum_{i=1}^m\frac{\partial x^i}{\partial x'^j}e_i\] \(X_p\)の座標変換はベクトルの１次変換と同じ形になります。接ベクトルの基底ベクトルを偏微分の記号で表すことで、座標変換はチェーンルールから自然に導出されます。

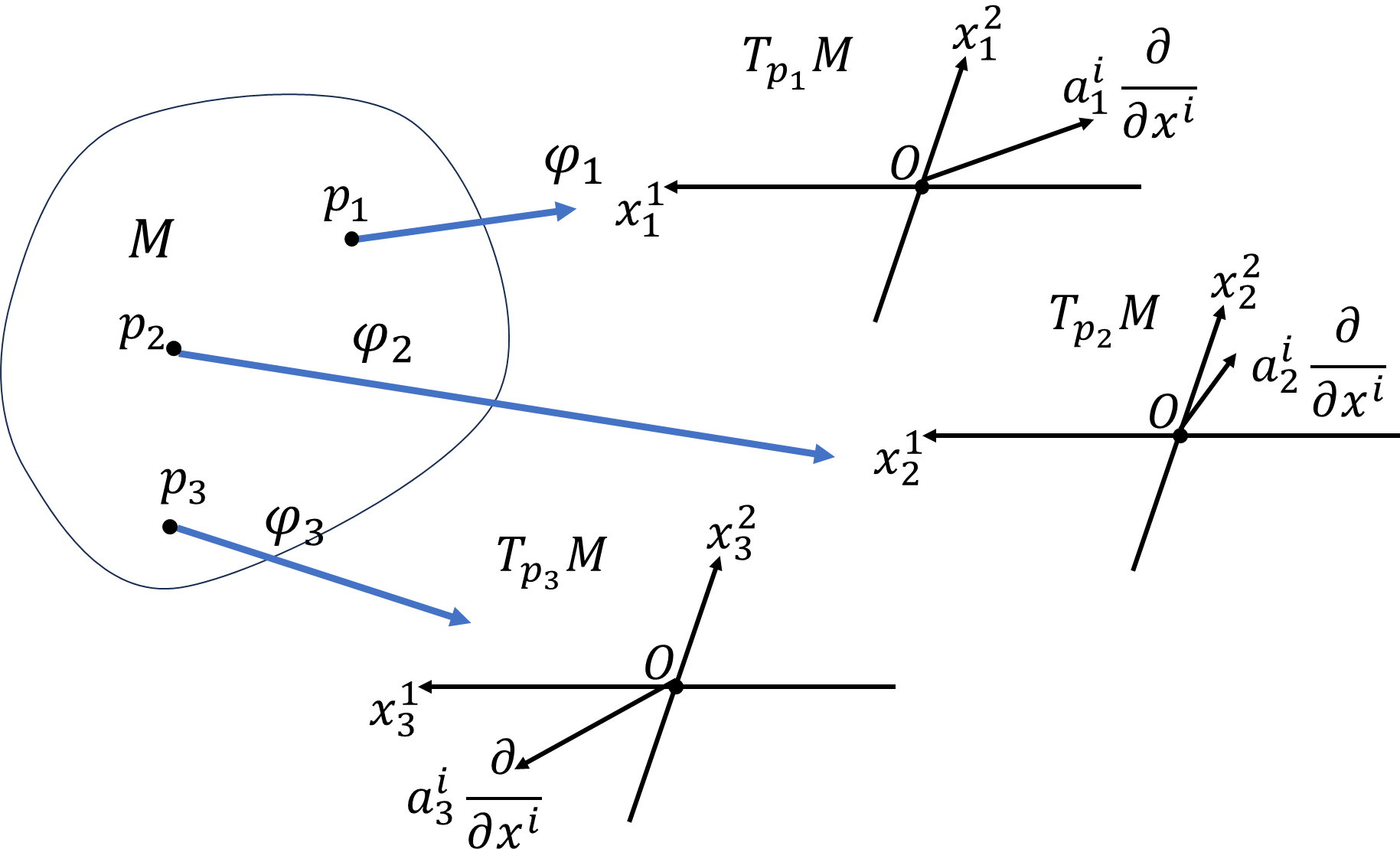
さらに接ベクトル束\(TM\)を \[TM:=\bigcup_{p\in M} T_pM\] で定義します。接空間を全て集めた集合です。多様体上の任意の点\(p\)に接空間\(T_pM\)があるということは、多様体上のいたる点で定義できるベクトルがあると思います。こそでベクトル場\(X\)を多様体上の点\(p\)から\(T_pM\)の接ベクトルを１つ取る写像とします。 \[X:p\to X_p\in T_pM\] ベクトル場\(X\)は接ベクトル束\(TM\)の断面などと言われます。\(1\)次元多様体をイメージすると、点\(p_i\)に対応する接空間\(T_pM\)をファイバー(繊維)と見立てます。そのファイバーを集めて束にしたものが接ベクトル束\(TM\)です。\(TM\)の断面には\(T_pM\)の元\(X_p\)が見えることからこのように表現されていると思われます。抽象的な話はこれくらいにして、実態として、ベクトル場は、曲線\(c(t)\)上の微分演算子と定義できます。 \[X:=\frac{d}{dt}\] 多様体上の点\(p\)を指定することで、 \[X_p=\left.\frac{d}{dt}\right|_{t=t_p}\] 接ベクトルになるので、ベクトル場は確かに\(T_pM\)から１つ接ベクトルを取ってくる写像となっています。ベクトル場を局所座標\(\varphi(x^1,x^2)\)を使って表してみましょう。曲線\(c(t)\)は局所座標で、\(\varphi\circ c(t)=(x^1(t),x^2(t))\)と表すことにすれば、 \[X=\frac{dx^1(t)}{dt}\frac{\partial}{\partial x^1}+\frac{dx^2(t)}{dt}\frac{\partial}{\partial x^2}\] 係数部分の\((\frac{dx^1}{dt},\frac{dx^2}{dt})\)は局所座標のスカラー値関数なので\(X^1(x^1,x^2),X^2(x^1,x^2)\)と表し、 \[X=X^1(x^1,x^2)\frac{\partial}{\partial x^1}+X^2(x^1,x^2)\frac{\partial}{\partial x^2}\] 局所座標では本来のベクトル場と同じ意味のベクトル場になっていますね。