楽しい科学（理論）チャンネル

\((0,1)\)開区間上の関数\(f=x^2\)を積分します。 \[\int_{0}^1fdx=\left[\frac{x^3}{3}\right]_{0}^1=\frac{1}{3}\] \(2x=y\)となる新たな座標\(y\)での積分は、 \[\int_{0}^2f\frac{dx}{dy}dy=\int_{0}^2\frac{y^2}{4}\frac{dy}{2}=\frac{1}{8}\left[\frac{y^3}{3}\right]_{0}^2=\frac{1}{3}\] この結果はもちろん正しいですが、積分の定義が座標に依っているという見方もできます。開線分\(L\)に以下のような座標軸\(x,y\)で測って、関数\(f:L\to\mathbb{R}\)の積分を

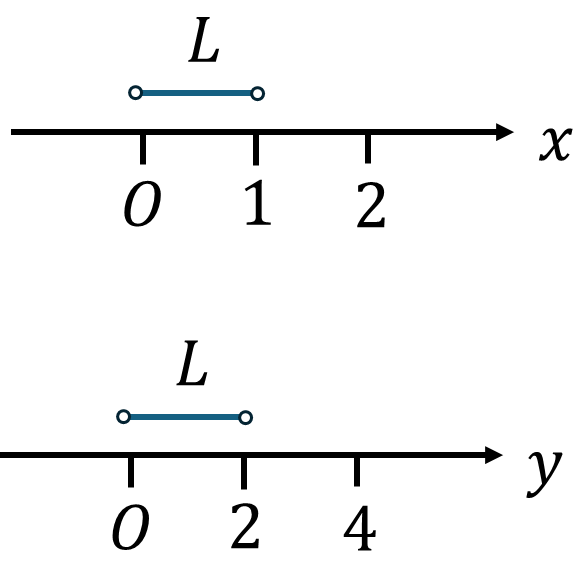
\(\varphi_1=x\)の座標を用いた場合は、 \[\int_{\varphi_1(L)}f\circ\varphi_1^{-1}dx\] と積分を定義しているのに対して、\(\varphi_2=y\)の座標では \[\int_{\varphi_2(L)}f\circ\varphi_2^{-1}\frac{dx}{dy}dy\] と定義しなくてはなりません。開線分\(L\)を\((0,1)\)開区間と定義していれば、\(y\)の座標での積分をただの座標変換したものとみることができますが、多様体風に言うと、開線分\(L\)にどの座標\(\varphi_i\)を用いるかで、積分の定義を変えなければならない。もしくは、積分の定義を、 \[\int_{\varphi_i(L)}f\circ\varphi_i^{-1} dx^i\] で統一する代わりに積分値が座標の取り方で変わってしまうという状況です。

　余接ベクトル\(\omega_p\)を多様体上のすべての点\(p\)で定義して、それらがなめらかにつながっているものを1次微分形式といいます。１次微分形式の導入によって積分の定義をきれいに座標に依らず定義することができます。詳細な定義は後でやりますが、 \[\omega=a_1dx^1=a_2dx^2\] となるような１次微分形式\(\omega\)が定義できれば、定義より、 \[a_1=a_2\frac{dx^2}{dx^1},\ a_2=a_1\frac{dx^1}{dx^2}\] が成り立ちます。これにより座標に依らず積分を \[\int_L\omega=\int_{\varphi_i(L)}a_idx^i\] と定義できます。 \[\int_{\varphi_1(L)}a_1dx^1=\int_{\varphi_2(L)}a_1\frac{dx^1}{dx^2}dx^2=\int_{\varphi_2(L)}a_2dx^2\] と簡単に確かめることができます。

　円周\(S^1\)少なくとも2つのチャートが必要になります。積分をするためには座標が必要なので、チャート上で積分をしなければなりません。

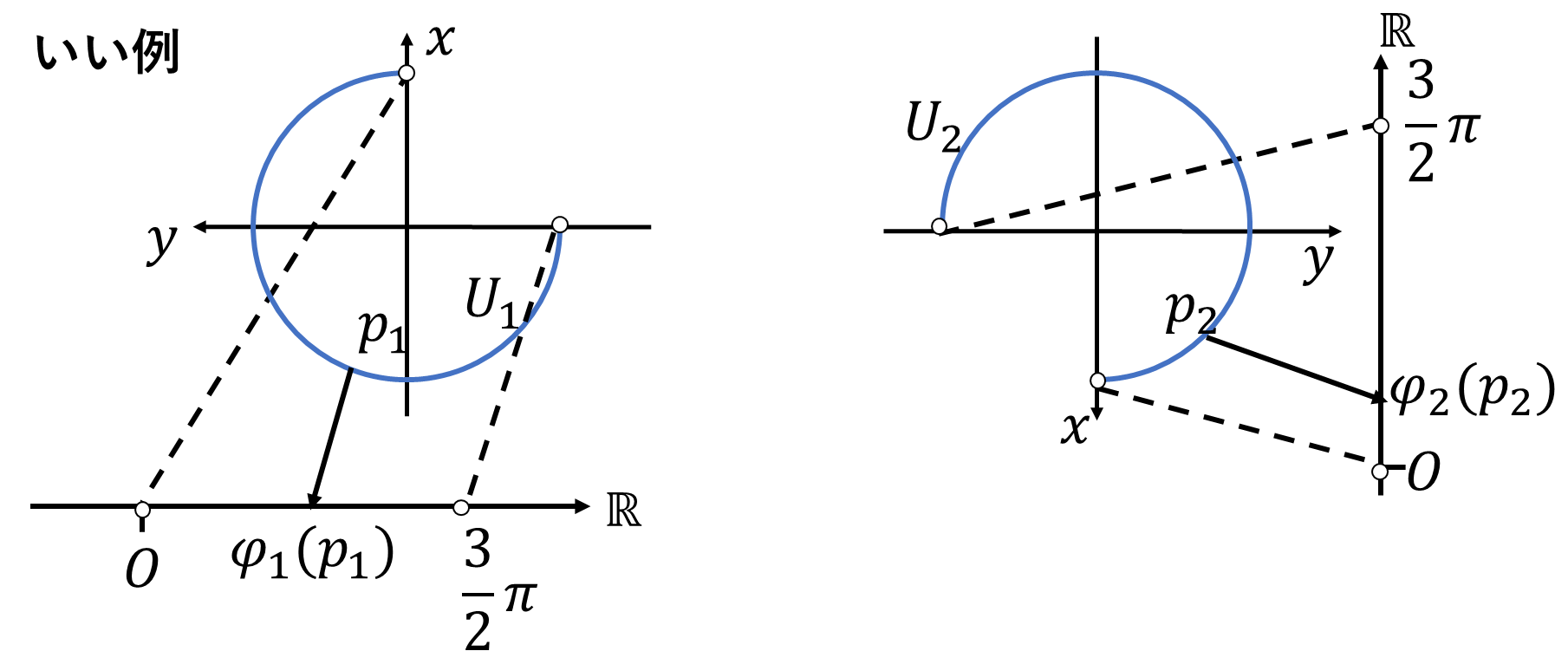
　開被覆\(U_1,U_2\)での積分値を足してしまうと、\(U_1\cap U_2\)の部分が２回分足されてしまうので、 \[\int_{S^1}\omega=\int_{U_1}\omega+\int_{U_2}\omega-\int_{U_1\cap U_2}\omega\] このように貼り合わせ部分では足しすぎた積分値を引かなければなりません。別にこれでもいいのですが、 \[\phi_i(p):=\begin{cases}1&p\in U_i\setminus U_1\cap U_2\ (i=1,2) \\\frac{1}{2}&p\in U_1\cap U_2 \\0&p\notin U_i\end{cases}\] で定義される1の分割を用いれば、 \[\int_{S^1}\omega=\sum_{i=1}^2\int_{U_i}\phi_i\omega\] このように何も考えず、各チャートでの\(\varphi_i\omega\)の積分値の総和が多様体上での積分値とすることができます。後々外微分という操作を導入するために、１の分割もなめらかに作る必要がありますが、ここでは、１の分割を用いる目的を理解してもらえればいいです。