楽しい科学(理論)チャンネル
1の分割の定義
立体的な図を作りたかったですが、うまく作れなかったです。多様体\(M\)を青色の線分で表しています。
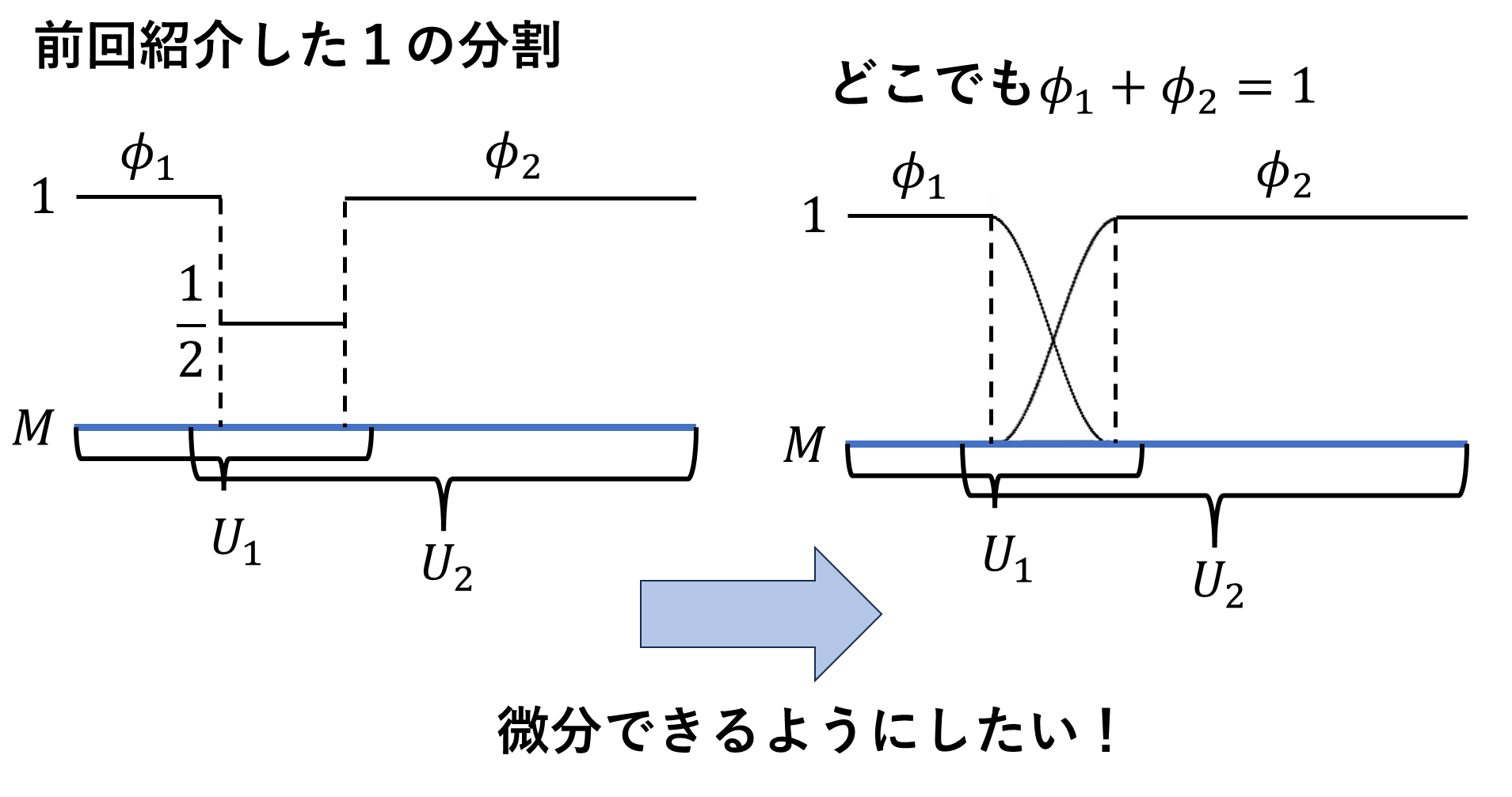
前回、多様体上の関数、1の分割\(\phi_i\)を開被覆\(U_i\)とセットの関数で、常に\(\phi_1+\phi_2=1\)を満たすために\(U_1\cap U_2\)で\(\phi_i=1/2\)としましたが、これを微分可能な関数で、実現していきます。1つだけ個人的にややこしい言葉、開被覆について、以下の特別ルールを定めます。
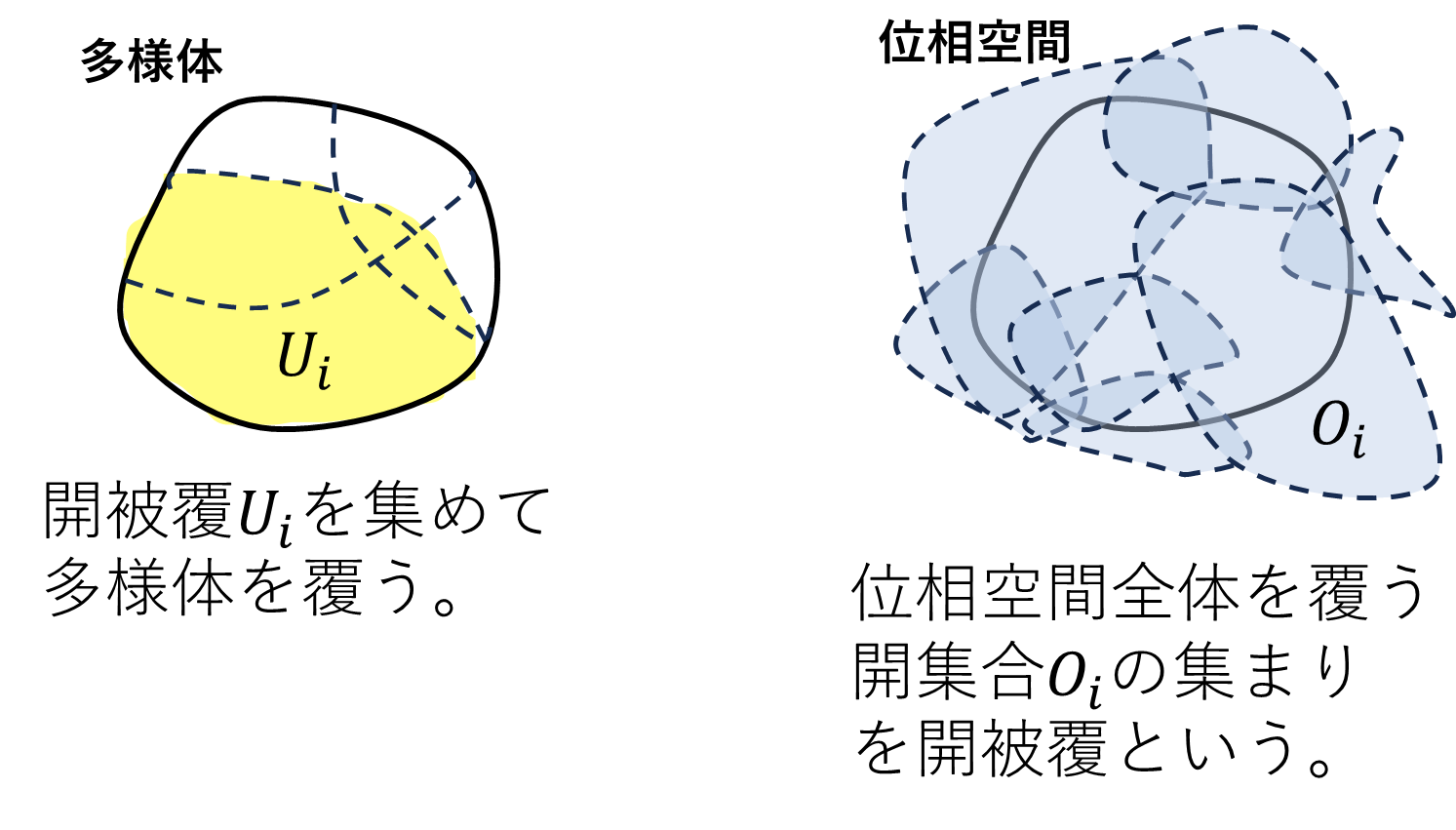
多様体に開被覆という言葉があります。
\[M=\bigcup_{\lambda\in\Lambda} U_\lambda\]
となる\(U_\lambda\)を開被覆と呼びます。しかし位相空間にも開被覆という言葉があります。
\[X\subset\bigcup_{\lambda\in\Lambda}O_\lambda\]
を満たす開集合系\(\{O_\lambda\}_{\lambda\in\Lambda}\)を開被覆といいます。\(X\)が空間全体の場合、\(O_\lambda\)が\(X\)の外にはみ出ることを考えず、
\[X=\bigcup_{\lambda\in\Lambda}O_\lambda\]
を満たす、開集合\(O_\lambda\)の集まり\(\{O_\lambda\}_{\lambda\in\Lambda}\)を開被覆といいます。\(U_\lambda\)、\(O_\lambda\)どちらも開集合ですが、\(U_\lambda\)には、ユークリッド空間への同相写像\(\varphi_\lambda\)がセットになっているところや、\(O_\lambda\)は位相空間が全体集合でなければ、\(X\)からはみ出て覆ってもよい点で若干ニュアンスが異なります。このページだけのルールで、位相空間における開被覆を「\(X\)全体を覆う開集合」と呼びます。開被覆と言ったら今まで通りの多様体を覆う開集合で、ユークリッド空間の開集合への同相写像が設定されたものというイメージでよいです。
**1の分割(簡易版)**
コンパクトな\(C^r\)級多様体\(M\)の
\[M=U_1\cup U_2\cup\cdots\cup U_k\]
となる有限個の開被覆\(\{U_i\}_{i=1}^k\)について、多様体上の\(C^r\)級関数\(\{\phi_i\}_{i=1}^k\)が
(i) \(\mathrm{supp}(\phi_i)\subset U_i\)
(ii) \(0\le\phi_i\le1\)
(iii) 多様体上の任意の点\(p\)で一の分割を全て足すと1になる。
\[\sum_{i=1}^k\phi_i(p)=1\]
を満たすとき\(\phi_i\)を1の分割と呼ぶ。(一般には、コンパクトより緩い条件で1の分割は存在する。)
初めにコンパクトについて説明する必要があるでしょう。多様体\(M\)の開被覆は無限にあるかもしれません。開被覆の集合を\(\{U_\lambda\}_{\lambda\in\Lambda}\)とします。から有限個の開被覆を取り出して\(M\)を被覆できるとき、
\[M=U_1\cup U_2\cup \cdots\cup U_k\]
\(M\)をコンパクト多様体といいます。コンパクトという概念は、位相空間の時点で定義できる概念で、
\[X\subset\bigcup_{\lambda\in\Lambda}O_\lambda\]
となる任意の全体を覆う開集合\(\{O_\lambda\}_{\lambda\in\Lambda}\)から、有限個で全体を覆えるとき、
\[X\subset\bigcup_{i=1}^kO_i\]
\(X\)はコンパクトです。
1の分割の条件(i)を見ていきます。まずは台\(\mathrm{supp}\)の定義を見てみます。
\[\mathrm{supp}(f):=\overline{\{x\in X\ |\ f(x)\neq0\}}\]
\(\mathrm{supp}\)は、関数\(f\)が0にならない点全ての閉包となります。閉包とは、境界点も集合に含ませる操作です。例えば、開区間\(A=(2,4)\)の閉包は、
\[\overline{A}=\overline{(2,4)}=[2,4]\]
となります。つまり1つ目の条件
\[\mathrm{supp}(\phi_i)\subset U_i\]
\(i\)番目の1の分割の0以上の点全体の集合は、\(i\)番目の開被覆の部分集合になっているということです。開被覆\(U_i\)の外では、\(\phi_i\)は\(0\)であるとも言えますね。条件(ii)(iii)は0以上1以下の関数で、その総和が1になるということですね。そのような都合の良い関数があるのか?証明してみます。
隆起関数
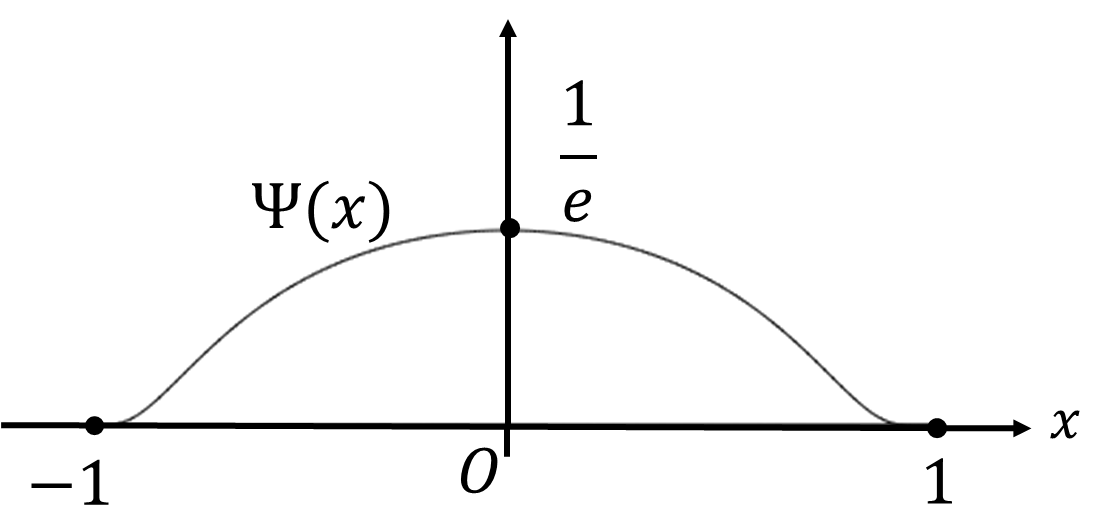
例えば、隆起関数\(\Psi(x)\)
\[\Psi(x)=\begin{cases}\exp\left(-\frac{1}{1-x^2}\right)&x\in(-1,1)
\\0&x\notin(-1,1)\end{cases}\]
の台は、
\[\mathrm{supp}(\Psi(x))=\overline{(-1,1)}=[-1,1]\]
です。\(\exp\left(-\frac{1}{1-x^2}\right)\)とは、\(e^{-\frac{1}{1-x^2}}\)のことです。指数の部分が複雑だと指数の部分が見づらくなるので、このような記法が使われます。これは\(C^\infty\)関数です。示していきます。
\[\frac{d\Psi}{dx}=\frac{2x}{(1-x^2)^2}\Psi\]
\[\frac{d^2\Psi}{dx^2}=\frac{2(1-x^2)^4+4x^2}{(1-x^2)^4}\Psi+\frac{4x^2}{(1-x^2)^4}\Psi\]
\[\cdots\]
\[\frac{d^n\Psi}{dx^n}=P_n(x)\frac{1}{(1-x^2)^{2n}}\exp\left(-\frac{1}{1-x^2}\right)\]
\(P_n(x)\)は\(x\)の多項式です。\(|x|\lt1,\ 1\lt|x|\)では、\(C^\infty\)級であることは明らかですので、\(n\)階導関数が、\(x=\pm1\)で連続か見てみます。多項式の部分は\(P_n(1)=P\)の定数となります。
\[\lim_{x\to1-0}\frac{1}{(1-x^2)^{2n}}\exp\left(-\frac{1}{1-x^2}\right)\]
\(a=\frac{1}{1-x^2}\)とすると、
\[=\lim_{a\to\infty}\frac{a^{2n}}{e^a}=0\]
べき乗より指数関数の方が増大の幅が大きいので0に収束します。\(x=-1\)の方も同様に\(0\)に収束します。\(n\)階微分が\(x=\pm1\)で連続なので、\(x=\pm1\)で\(n-1\)階まで微分可能ということになります。同じことを\(n+1\)階導関数についてやれば、\(x=\pm1\)で\(n\)階まで微分可能となります。依って\(\Psi(x)\)は\(C^\infty\)関数です。
コンパクト空間の性質
コンパクトには様々な良い性質がありますが、そのほんの一部を紹介します。
コンパクト集合\(X\)の部分閉集合\(K\)はコンパクトになります。\(X\in\mathfrak{O}\)位相空間における閉集合を定義していませんでしたが、閉集合を開集合の補集合とします。つまり、\(X\)の任意の開集合\(O\)について、
\[A=X\setminus O\]
となる、\(A\)を閉集合と呼ぶことにします。特に\(\varnothing=X\setminus X,X=X\setminus\varnothing\)なので集合全体や空集合も閉集合となります。全体集合や閉集合は開集合にも閉集合にもなりえます。また開集合は閉集合の補集合なので、閉集合系\(\mathfrak{A}\)を定めると、開集合も定まり位相を決定することもできます。
証明 コンパクト空間\(X\)の部分閉集合\(K\)はコンパクト
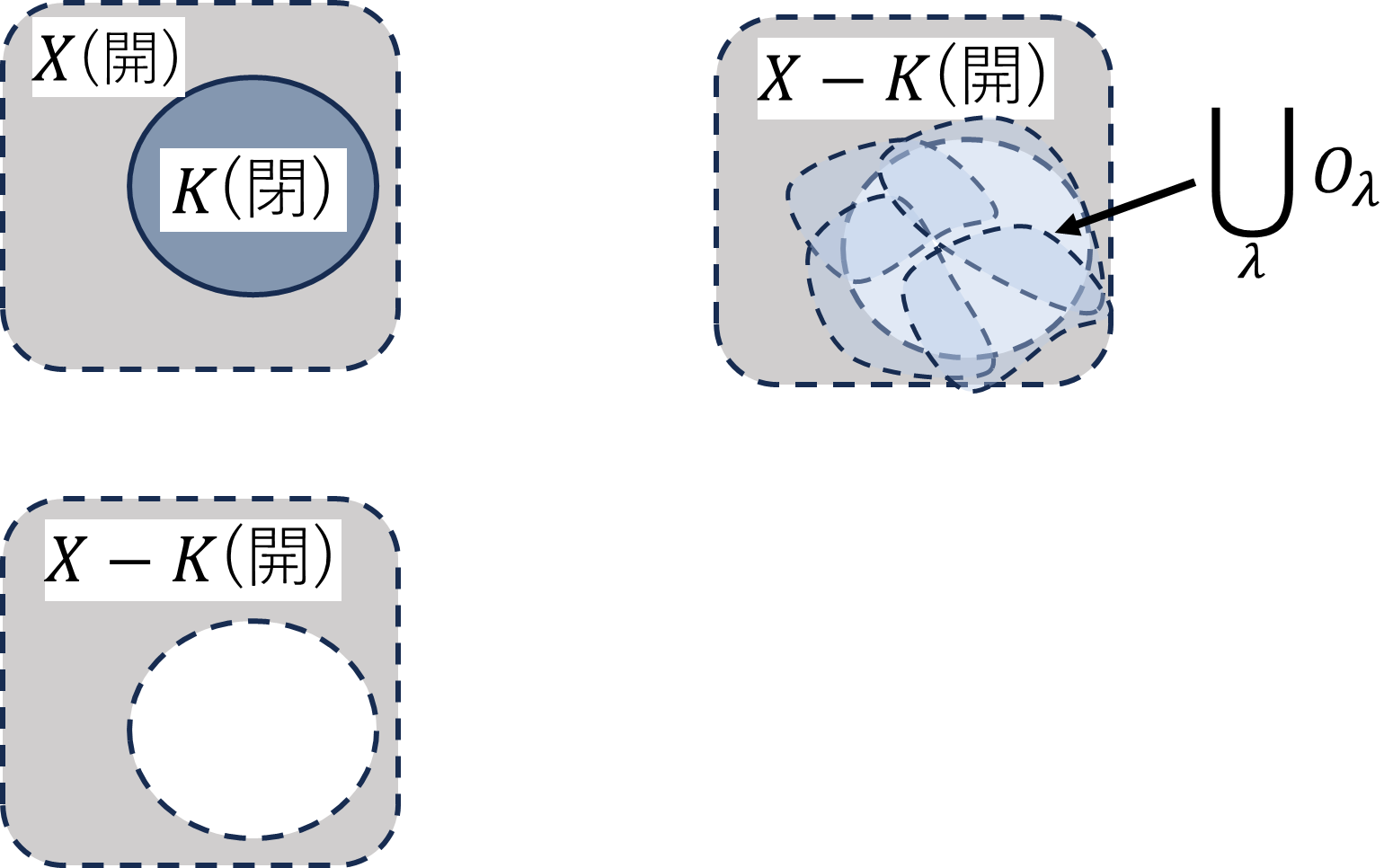
位相空間\(X\)について、全体集合\(X\)は位相の公理から開集合です。\(X\)の任意の部分閉集合\(K\)の補集合は開集合となります。(図より閉部分\(K\)を取り出すと、閉包部分は\(K\)に含まれるので、残された\(X\setminus K\)は開となります。)
\[\mathop{X}_{開}\setminus\mathop{K}_{閉}=\underbrace{X\setminus K}_{開}\]
つまり、\(X\setminus K\)も位相空間上の開集合です。\(K\)全体を覆う開集合を\(\{O_\lambda\}_{\lambda\in\Lambda}\)とします。ただし\(O_\lambda\in \mathfrak{O}\)です。\(X\)全体を覆う開集合として、
\[X=\bigcup_{\lambda\in\Lambda}O_\lambda\cup (X\setminus K)\]
というものを取ってみます。\(X\)はコンパクトなので、\(\{O_\lambda\}_{\lambda\in\Lambda},X\setminus K\)から有限個を選んで全体を覆うことができるので、
\[X=\bigcup_{i=1}^kO_i\cup (X\setminus K)\]
この手順を踏むことで、\(K\)を任意の覆う開集合\(\{O_\lambda\}_{\lambda}\)から有限個の開集合で全体を覆えているので、
\[K=O_1\cup O_2\cup\cdots\cup O_k\]
\(K\)もコンパクトとなります。
終わり
証明 コンパクト空間\(X\)と同相な空間\(Y\)はコンパクトである。
\((X,\mathfrak{O}_{X}),(Y,\mathfrak{O}_{Y})\)を同相な位相空間とします。その同相写像を
\[f:X\to Y\]
とします。同相写像は全単射でもあるので、任意の\(x\in X\)に対して、\(y=f(x)\)が1つだけ存在します。その逆も成り立ち、\(X\)全体の像が\(Y\)になり、\(Y\)全体逆像像が\(X\)になります。
\[f(X)=Y,\ f^{-1}(Y)=X\]
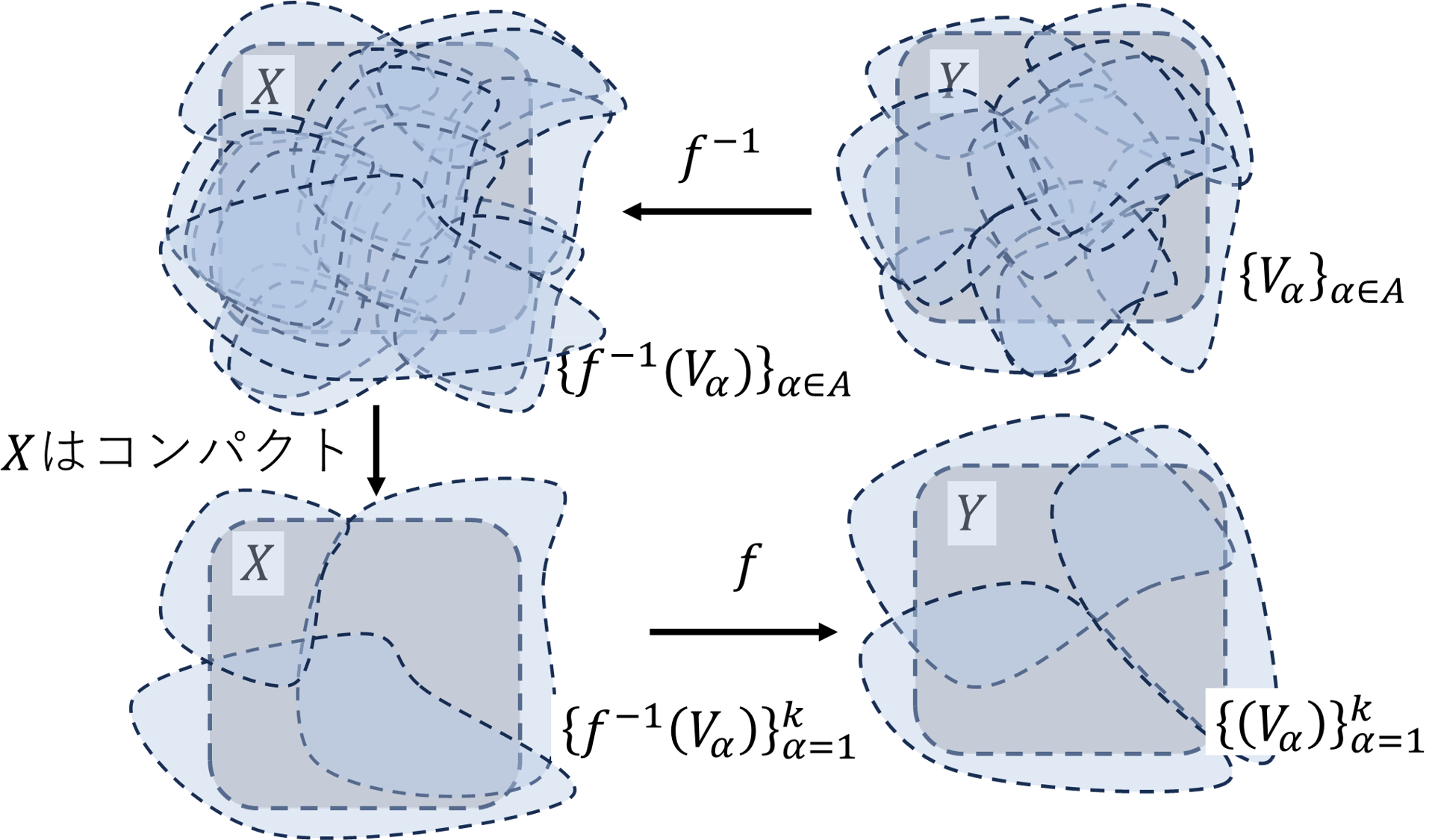
\(Y\)を覆う開集合全体を、\(\{V_\alpha\}_{\alpha\in A}\)とします。この開集合は有限個かわかりません。この開集合をすべて逆像を取ると、\(X\)全体を覆う開集合となります。任意の点\(y\in Y\)はいずれかの\(V_\alpha\)に含まれ、\(f^{-1}\)により、\(X\)上の点に写されます。全単射なので、すべての点\(y\)を移せば\(X\)上のすべての点に対応するためです。
\[X\subset\bigcup_{\alpha\in A}f^{-1}(V_\alpha)\]
\(X\)はコンパクトなので、有限個の開集合で覆うことができます。
\[X\subset\bigcup_{\alpha=1}^kf^{-1}(V_\alpha)\]
先ほどと同じ理由で、\(\{f^{-1}(V_\alpha)\}_{\alpha=1}^k\)全体をすべて\(f\)で写せば\(Y\)全体を覆う開集合となります。
\[Y\subset\bigcup_{\alpha=1}^kf(f^{-1}(V_\alpha))=\bigcup_{\alpha=1}^kV_\alpha\]
この手順で、\(Y\)も任意の全体を覆う開集合から、有限個の開集合で全体を覆えるのでコンパクトとなります。
終わり
コンパクト空間の部分閉集合はコンパクト!コンパクト空間と同相な空間もコンパクト!この2つは覚えておきましょう。今回は同相写像で証明しましたが、実はもっと緩い条件で成立します。コンパクト空間に連続な空間はコンパクト性を引き継ぎます。私個人として、証明を見て確かに成立しているのを確かめましたが、全単射でもないし、位相構造が違うのに成立していることに違和感を感じてしまいます。
コンパクト多様体における1の分割
準備が終わりました。いよいよコンパクト多様体\(M\)における1の分割の存在を証明します。式の見やすさ重視で\(M\)の次元は2次元とします。開円盤を使った照明となりますが、次元は、
\[D=\left\{(x^1,x^2\cdots,x^m)\ \middle|\ (x^1)^2+(x^2)^2+\cdots+(x^m)^2\lt a^2\right\}\]
このように簡単に拡張できるので、2次元で十分と判断しました。
証明 コンパクト多様体に1の分割が存在する。
先ほどの隆起関数\(\Psi(x)\)は\(\mathrm{supp}(\Psi(x))=[-1,1]\)を満たす\(C^\infty\)級関数です。これを閉円盤を台とする関数に拡張します。

\(2\)次元ユークリッド空間上で点\(p=(p^1,p^2)\)を中心とする円盤領域\(D\)を、
\[D_{(p)}=\left\{(x^1,x^2)\ \middle|\ (x^1-p^1)^2+(x^2-p^2)^2\lt a^2\right\}\]
とします。その閉包は
\[\overline{D}_{(p)}=\left\{(x^1,x^2)\ \middle|\ (x^1-p^1)^2+(x^2-p^2)^2\le a^2\right\}\]
です。
\[f_{(p)}(x^1,x^2):=\frac{1}{a^2}\{(x^1-p^1)^2+(x^2-p^2)^2\}\]
という\(C^\infty\)級関数を定義します。円盤内なら\(f\lt1\)円盤の外なら、\(1\lt f\)となる関数です。関数\(f\)を隆起関数に合成します。その関数を\(\psi\)とします。\(C^\infty\)級関数の合成関数なので、この関数も\(C^\infty\)級です。(そういうことにしておきます。)
\[\psi_{(p)}(x^1,x^2)=\Psi\circ f_{(p)}(x^1,x^2)=\begin{cases}\exp\left(-\frac{1}{1-(f_{(p)}(x^1,x^2))^2}\right)&(x^1,x^2)\in D_{(p)}
\\0&(x^1,x^2)\notin D_{(p)}\end{cases}\]
\(\mathrm{supp}(\psi(x^1,x^2))=\overline{D}\)なので、この合成関数は、台を\([-1,1]\)から円盤領域\(D\)に拡張した隆起関数といえます。
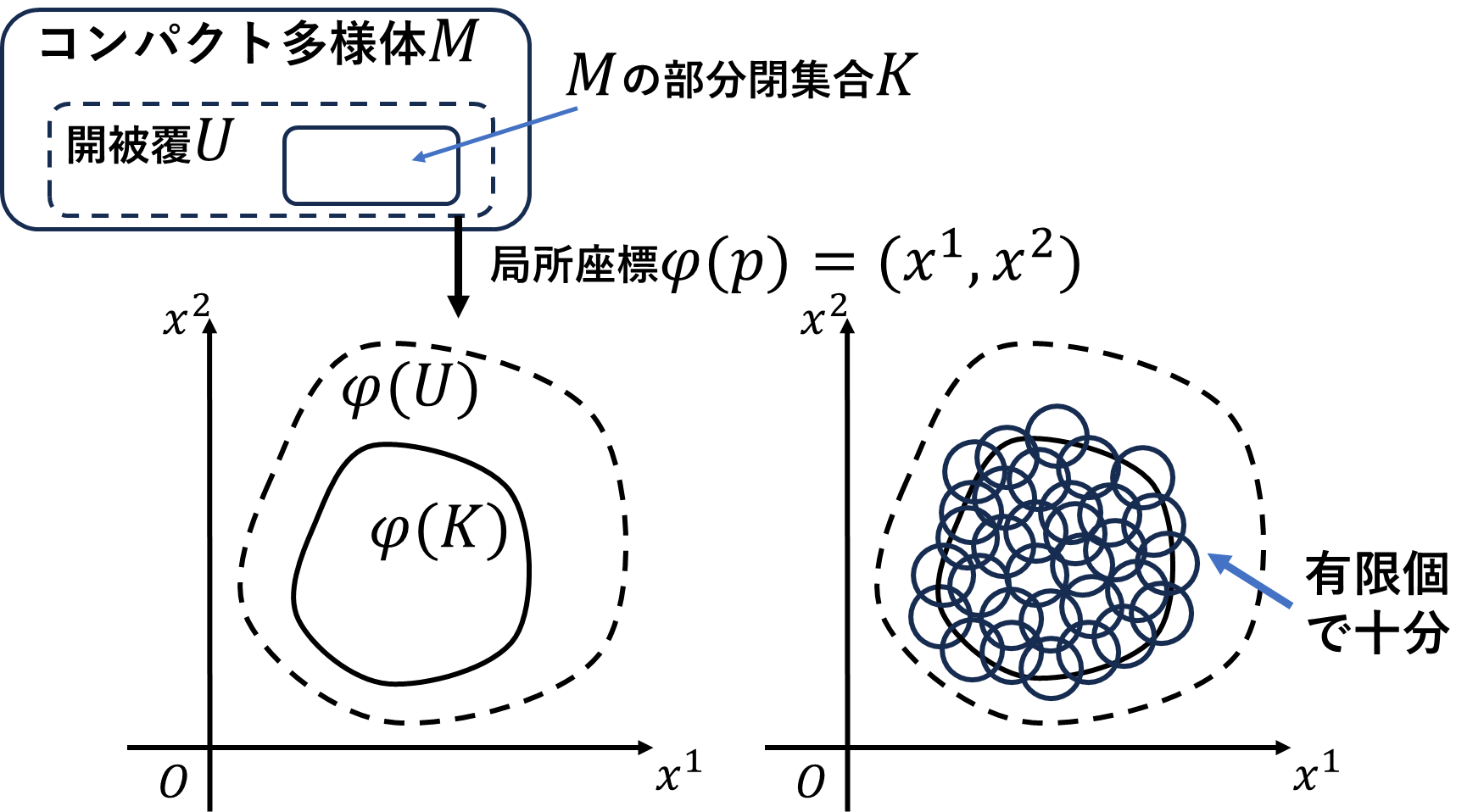
コンパクト多様体\(M\)の開被覆\(U\)のさらに内部に閉集合\(K\)を取ります。\(K\)は\(M\)の部分閉集合なのでコンパクトです。閉集合\(K\)をチャート\((U,\varphi)\)に写します。その閉集合を\(\varphi(K)\)とします。コンパクト空間\(K\)と\(\varphi(K)\)は同相なので、\(\varphi(K)\)もコンパクトとなります。\(\varphi(K)\)上のすべての点\(p_{\lambda}\)を中心とする開円盤の集合\(\{D_{(p_\lambda)}\}_{\lambda\in\Lambda}\)で\(\varphi(K)\)を覆うことができます。開円盤が\(\varphi(U)\)からはみ出ないように半径\(a\)は小さめにとっておきます。しかも\(\varphi(K)\)はコンパクトなので、任意個の開円盤で\(\varphi(K)\)を覆うことができます。開円盤をの閉円盤にしても覆うことができます。
\[\varphi(K)\subset\bigcup_{i=1}^kD_{(p_i)}\subset\bigcup_{i=1}^k\overline{D}_{(p_i)}\subset \varphi(U)\]
関数\(\psi_{(p_i)}\)は点\(p_i\)を中心とする閉円盤\(\overline{D}_{(p_i)}\)を台とする(閉円盤上で、\(\psi_{(p_i)}\neq0\))\(C^\infty\)級関数なので、その総和を多様体上の関数\(h\)とすれば、(本来\(U\)上に制限しているので、\(h|_U\)などと書くべきですが、)
\[h\circ\varphi^{-1}(x^1,x^2)=\sum_{i=1}^k\psi_{(p_i)}\gt0\iff(x^1,x^2)\in \bigcup_{i=1}^k D_{(p_i)}\]
\[h\circ\varphi^{-1}(x^1,x^2)=\sum_{i=1}^k\psi_{(p_i)}=0\iff(x^1,x^2)\notin \bigcup_{i=1}^k D_{(p_i)}\]
を満たします。つまり有限個の閉円盤で覆った部分がこの関数の台となります。
\[\mathrm{supp}(h\circ\varphi^{-1}(x^1,x^2))=\bigcup_{i=1}^k \overline{D}_{(p_i)}\]
つまり以下の関係が成り立ちます。
\[\varphi(K)\subset \mathrm{supp}(h\circ\varphi^{-1}(x^1,x^2))\subset \varphi(U)\]
これを多様体に引き戻します。\(\varphi^{-1}\)同相写像なので、この包含関係は崩れません。(同相写像は粘土を切り貼りなしで変形するようなものなので、\(U\)内部の閉集合が外にはみ出したりしません。)
\[\varphi^{-1}(\varphi(K))\subset \varphi^{-1}(\mathrm{supp}(h\circ\varphi^{-1}(x^1,x^2)))\subset \varphi^{-1}(\varphi(U))\]
\[K\subset \mathrm{supp}(h(p))\subset U\]
さらに\(M\)はコンパクトなので、チャート\((\varphi_i,U_i)\)も有限個を選べて、そのすべてで今と同じ操作をして、多様体上の有限個の関数、\(h_1(p),h_2(p),\cdots,h_l(p)\)を得ます。\(l\)個の開被覆\(U_i\)について、1の分割\(\phi_i\)を
\[\phi_i(p):=\frac{h_i(p)}{\sum_{j=1}^lh_j(p)}\]
と定義します。
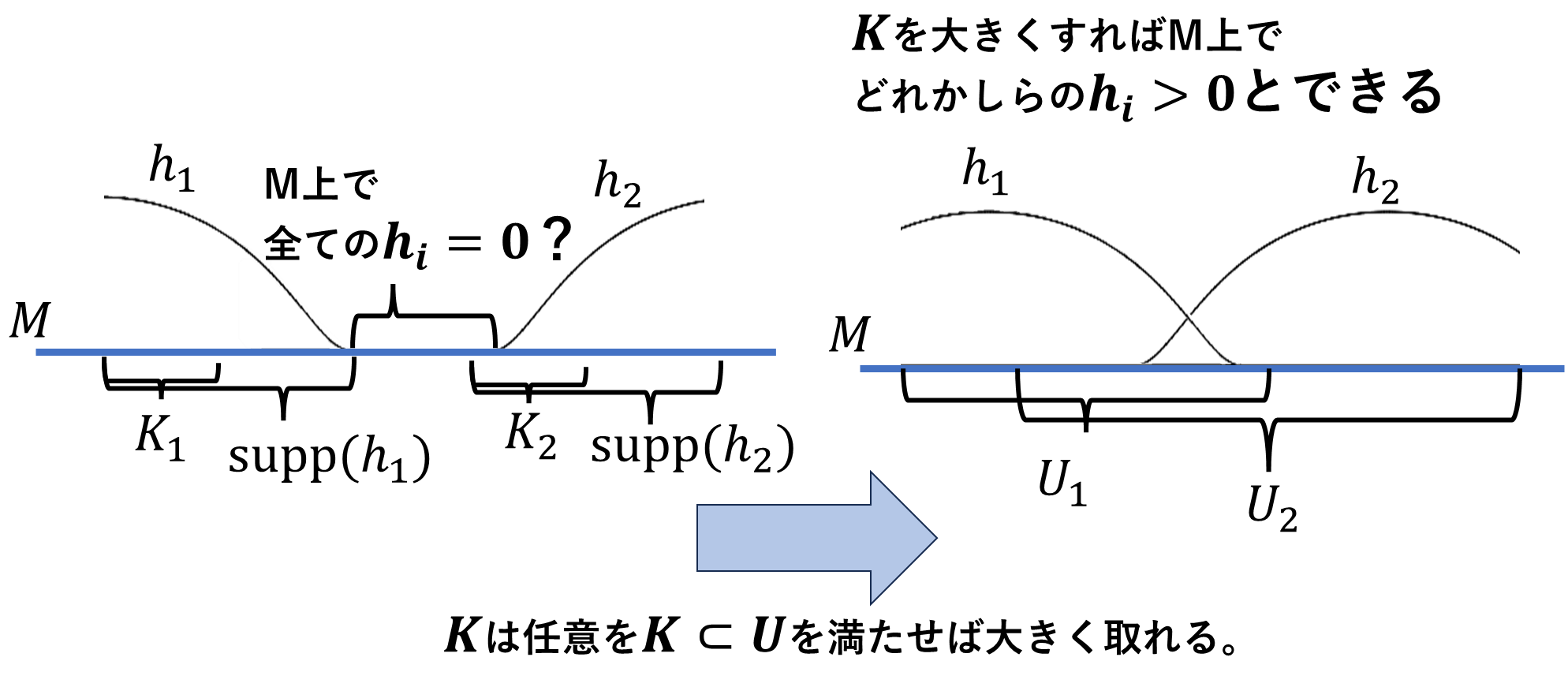
閉集合\(K\)は任意なので、\(K\subset U\)を満たす範囲で大きく取ることができます。多様体上の任意の\(p\)でどれかの\(h_i(p)\)を0以上にできるので、分母の\(\sum h_j\)は0になりません。隆起関数\(\psi\)は最大でも\(1/e\)の有限の値を取ります。コンパクトという条件のおかげで、\(h\)は\(h=\psi_1+\psi_2+\cdots+\psi_k\)で有限の値になります。1の分割の分母\(h_1+h_2+\cdots+h_l\)は無限大になりません。すべての\(\phi_i=0\)ということも起こりません。1の分割をすべて足すと、
\[\sum_{i=1}^l\phi_i(p)=\frac{\sum_{i=1}^lh_i(p)}{\sum_{j=1}^lh_j(p)}=1\]
以上から、
\[\begin{align}(\mathrm{i})\ \ &\mathrm{supp}(\phi_i(p))\subset U_i
\\(\mathrm{ii})\ \ &0\le\phi_i(p)\le1
\\(\mathrm{iii})\ \ &\sum_{i=1}^l\phi_i(p)=1\end{align}\]
を満たす\(C^r\)級関数\(\phi_i\)が存在する。







