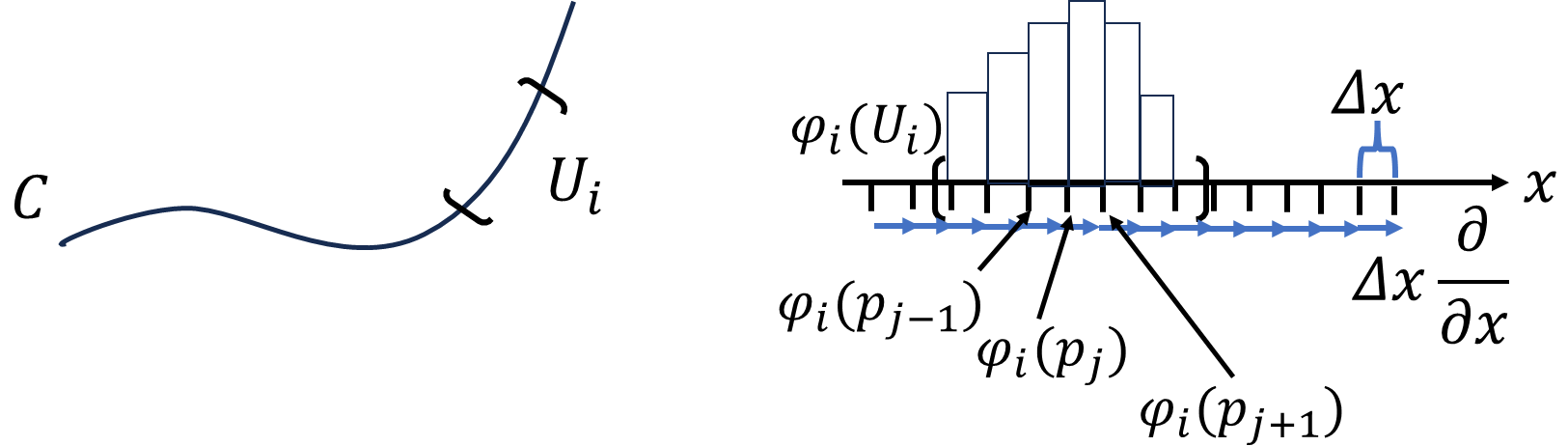
可微分多様体上の任意の点\(p\)での\(k\)個の接ベクトル\(X_1,X_2,\cdots,X_k\in T_pM\)をスカラーに写す写像\(\omega:(X_1,X_2,\cdots,X_k)\to\mathbb{R}\)が、
\((\mathrm{i})\)線形性
\(Y_i\in T_pM\)について、
\[\omega(X_1,X_2,\cdots, X_i+Y_i\cdots,X_k)\]
\[=\omega(X_1,X_2,\cdots, X_i\cdots,X_k)+\omega(X_1,X_2,\cdots,+Y_i\cdots,X_k)\]
またスカラー\(a\)について、
\[\omega(X_1,X_2,\cdots, aX_i\cdots,X_k)\]
\[=a\omega(X_1,X_2,\cdots, X_i\cdots,X_k)\]
\((\mathrm{ii})\)交代性
\[\omega(X_1,X_2,\cdots, X_i,\cdots,X_j\cdots,X_k)\]
\[=-\omega(X_1,X_2,\cdots, X_j,\cdots,X_i\cdots,X_k)\]
\((\mathrm{iii})\)滑らかさ
\(M\)上の滑らかなベクトル場\(Z_1,Z_2,\cdots,Z_k\)について、\(\omega(Z_{1},Z_2\cdots,Z_k)\)は多様体上の関数と見ることができて、
\[\omega(Z_1,\cdots,Z_k):p\mapsto\omega(Z_1,\cdots,Z_k)(p)\in\mathbb{R}\]
が\(C^r\)級である。
これら3つの条件を満たすとき、\(\omega:(X_1,X_2,\cdots,X_k)\to\mathbb{R}\)を\(k\)次微分形式と呼ぶ。
注意してほしいのは、\(X_i\)の添え字の\(i\)が下についているから双対ベクトルの成分というわけではなく、ただ単に\(i\)番目の接ベクトルです。接ベクトルを\(X,Y,Z,\cdots\)としていくとアルファベットが足りないためです。この説明だけでは何を言っているんだ、、、と思うと思います。テンソルを導入すればシンプルに話をまとめることができますが、今回の目的は、微分形式を理解することにあります。少し回りくどくやっていきます。1つずつ見ていきましょう。