楽しい科学(理論)チャンネル
2次微分形式
次に2次微分形式を見ていきます。初めに2つ\(\mathbb{R}^2\)上のベクトル\(\boldsymbol{k}=(k^1,k^2),\boldsymbol{l}=(l^1,l^2)\)を実数に写す線形写像\(f:(\boldsymbol{k},\boldsymbol{l})\mapsto\mathbb{R}\)を探します。ベクトルの和の写像はそれぞれのベクトルの写像の和と等しいので、\(\because f(\vec{a}+\vec{b})=f(\vec{a})+f(\vec{b})\)
\[f(\boldsymbol{k},\boldsymbol{l})=f(k^1\boldsymbol{e}_1+k^2\boldsymbol{e}_2,\boldsymbol{l})=f(k^1\boldsymbol{e}_1,\boldsymbol{l})+f(k^2\boldsymbol{e}_2,\boldsymbol{l})\]
さらにスカラーは写像の外に出せるので、\(\because f(k\vec{a})=kf(\vec{a})\)
\[f(\boldsymbol{k},\boldsymbol{l})=f(\boldsymbol{e}_1,\boldsymbol{l})k^1+f(\boldsymbol{e}_2,\boldsymbol{l})k^2\]
\(\boldsymbol{l}=(l^1,l^2)\)についても同様にして、
\[f(\boldsymbol{k},\boldsymbol{l})=f(\boldsymbol{e}_1,\boldsymbol{e}_1)k^1l^1+f(\boldsymbol{e}_1,\boldsymbol{e}_2)k^1l^2\]
\[+f(\boldsymbol{e}_2,\boldsymbol{e}_1)k^2l^1+f(\boldsymbol{e}_2,\boldsymbol{e}_2)k^2l^2\]
\(f(\boldsymbol{e}_{i_1},\boldsymbol{e}_{i_2})=f_{i_1i_2}\)とすることで、ちょっとだけ見通しをよくします。
\[f(\boldsymbol{k},\boldsymbol{l})=\sum_{i_1=1}^2\sum_{i_2=1}^2f_{i_1i_2}k^{i_1}l^{i_2}\]
これが成分を用いた2つのベクトルを実数に写す線形写像です。\(\boldsymbol{k},\boldsymbol{l}\)を\(m\)次元多様体の接ベクトル\(X_1,X_2\in T_pM\)に変えておきます。
\[f(X_1,X_2)=\sum_{i_1=1}^m\sum_{i_2=1}^mf_{i_1i_2}X_1^{i_1}X_2^{i_2}\]
更に交代性
\[f(X_1,X_2)=-f(X_2,X_1)\]
を満たす必要があります。ここで、符号関数\(\mathrm{sgn}(\sigma)\)や、一般化されたクロネッカーのデルタ\(\delta^{\mu_1\cdots \mu_k}_{\nu_1\cdots \nu_k}\)を使います。
\[\mathrm{sgn}(^{\mu_1\cdots \mu_k}_{\nu_1\cdots \nu_k})=\delta^{\mu_1\cdots \mu_k}_{\nu_1\cdots \nu_k}=\begin{cases}1&上下の文字列が偶置換\\-1&上下の文字列が奇置換\\0&上下の文字列が置換できない\end{cases}\]
どちらも同じ意味なので、好きな方を使ってください。定数\(f_{i_1i_2}\)を任意の定数\(g_{j_1j_2}\)を用いて、
\[f_{i_1i_2}=\sum_{j_1=1}^m\sum_{j_2=1}^m\delta^{j_1j_2}_{i_1i_2}g_{j_1j_2}\]
と表してみましょう。これにより、\(f_{i_1i_2}\)は交代性を獲得できます。
\[f_{i_2i_1}=\sum_{j_1=1}^m\sum_{j_2=1}^m\delta^{j_1j_2}_{i_2i_1}g_{j_1j_2}\]
\[-\sum_{j_1=1}^m\sum_{j_2=1}^m\delta^{j_1j_2}_{i_1i_2}g_{j_1j_2}=-f_{i_1i_2}\]
交代性を持った定数\(f_{i_1i_2}\)を用いることで、
\[f(X_2,X_1)=\sum_{i_1=1}^m\sum_{i_2=1}^mf_{i_1i_2}X_2^{i_1}X_1^{i_2}\]
\[=-\sum_{i_1=1}^m\sum_{i_2=1}^mf_{i_2i_1}X_1^{i_2}X_2^{i_1}=-f(X_1,X_2)\]
写像自体も交代性を獲得します。
\[\sum定数\times X_1の成分\times X_2の成分\]
の形を崩していないので、(i)の線形性も保っています。交代的な写像\(f\)を多様体上すべての点\(p\)に定義すれば、ベクトル場\(X_1,X_2\)を代入したスカラー値を\(f(X_1,X_2)\)を多様体上の関数と見ることができます。
\[\omega(X_1,X_2):p\mapsto\sum_{i_1=1}^m\sum_{i_2=1}^m\omega_{i_1i_2}X_1^{i_1}X_2^{i_2}\]
ベクトル場の成分はなめらかなので、この写像が\(C^r\)級である為には、\(\omega_{i_1i_2}\)がチャート上の関数であり、\(C^r\)級であればよいですね。これが2次微分形式です。記号も\(f\)から\(\omega\)に書き換えました。2次微分形式はベクトル場抜きで、1次微分形式の基底を用いて表すことができます。1次微分形式は
\[dx^i(X)=X^i\]
ベクトル場から、その方向の成分を取り出す写像なので、
\[\omega(X_1,X_2)=\sum_{i_1=1}^m\sum_{i_2=1}^m\omega_{i_1i_2}X_1^{i_1}X_2^{i_2}=\sum_{i_1=1}^m\sum_{i_2=1}^m\omega_{i_1i_2}dx^{i_1}(X_1)dx^{i_2}(X_2)\]
\[\omega(\Box_1,\Box_2)=\sum_{i_1=1}^m\sum_{i_2=1}^m\omega_{i_1i_2}dx^{i_1}(\Box_1)dx^{i_2}(\Box_2)\]
\(\Box_1,\Box_2\)には接ベクトルを代入できます。これが1次微分形式を用いた2次微分形式です。しかし2次以上の微分形式は専用の基底
\[dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}(\Box_1,\cdots,\Box_k)\]
\[=\sum_{\nu_1=1}^m\cdots\sum_{\nu_k=1}^m\delta_{1\cdots k}^{\rho_1\cdots\rho_k}dx^{\mu_1}(\Box_{\rho_1})\cdots dx^{\mu_k}(\Box_{\rho_k})\]
があります。ただし、\(\mu_1\lt\cdots\lt\mu_k\)です。ここにクロネッカーのデルタを掛けます。
\[=\sum_{\nu_1=1}^m\cdots\sum_{\nu_k=1}^m\delta_{1\cdots k}^{\rho_1\cdots\rho_k}\underbrace{\delta_{\mu_1\cdots\mu_k}^{\mu_1\cdots\mu_k}}_{=1}dx^{\mu_1}(\Box_{\rho_1})\cdots dx^{\mu_k}(\Box_{\rho_k})\]
\(\delta_{1\cdots k}^{\rho_1\cdots\rho_k}\)の\(\rho_1\cdots\rho_k\)を\(1\cdots k\)に並べ替えます。それと同じように\(\delta^{\mu_1\cdots\mu_k}_{{\mu_1\cdots\mu_k}}\)の下の添え字を並び替えます。どちらも交代性を持っている為この並び替えによって、微分形式の符号は変わりません。そしてできた新しい文字列を\(\nu_1\cdots\nu_k\)とします。
\[=\sum_{\nu_1=1}^m\cdots\sum_{\nu_k=1}^m\delta_{1\cdots k}^{1\cdots k}\delta^{\mu_1\cdots\mu_k}_{\nu_1\cdots\nu_k}dx^{\mu_1}(\Box_{\rho_1})\cdots dx^{\mu_k}(\Box_{\rho_k})\]
1次微分形式の基底も\(\nu_1\cdots\nu_k\)に並び替えれば、接ベクトルを代入できるスロットは\(1\cdots k\)に並び替えられるので、
\[dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}(\Box_1,\cdots,\Box_k)\]
\[=\sum_{\nu_1=1}^m\cdots\sum_{\nu_k=1}^m\delta^{\mu_1\cdots\mu_k}_{\nu_1\cdots\nu_k}dx^{\nu_1}(\Box_{1})\cdots dx^{\nu_k}(\Box_{k})\]
代入されている接ベクトルの交代性、1次微分形式の基底の交代性に着目した定義両方使います。定義が一見複雑そうなので、2次微分形式の基底を見てみます。気合を入れてみていきましょう。
\[dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)=\sum_{\rho_1=1}^m\sum_{\rho_2=1}^m\delta_{12}^{\rho_1\rho_2}dx^{\mu_1}(\Box_{\rho_1})dx^{\mu_2}(\Box_{\rho_2})\]
\(\delta^{45}_{12},\delta^{76}_{12}\)などの置換不可能な場合はクロネッカーのデルタは0になり、0でないものだけ集めると、
\[dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)=dx^{\mu_1}(\Box_1)dx^{\mu_2}(\Box_2)-dx^{\mu_2}(\Box_1)dx^{\mu_1}(\Box_2)\]
このようになります。定義より、接ベクトルの交換や
\[dx^{\mu_1}\wedge dx^{\mu_2}(Y,X)=dx^{\mu_1}(Y)dx^{\mu_2}(X)-dx^{\mu_2}(Y)dx^{\mu_1}(X)\]
\[=-dx^{\mu_1}\wedge dx^{\mu_2}(X,Y)\]
1次微分形式の基底の交換に対して
\[dx^{\mu_2}\wedge dx^{\mu_1}(\Box_1,\Box_2)=dx^{\mu_2}(\Box_1)dx^{\mu_1}(\Box_2)-dx^{\mu_1}(\Box_1)dx^{\mu_2}(\Box_2)\]
\[=-dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)\]
交代性交代性を持ちます。これはクロネッカーのデルタを用いた微分形式の基底の定義においては、接ベクトルの交換は、\(\nu\)の添え字の交換、1次微分形式の交代は\(\mu\)の添え字の交換に対応しています。先ほど微分形式の定義から導いた、2次微分形式\(\omega:(X_1,X_2)\mapsto\mathbb{R}\)を2次微分形式の基底を用いて表してみましょう。
\[\omega(\Box_1,\Box_2)=\sum_{i_1=1}^m\sum_{i_2=1}^m\omega_{i_1i_2}dx^{i_1}(\Box_1)dx^{i_2}(\Box_2)\]
\(1,2,\cdots,m\)の中から、\(\mu_1\lt\mu_2\)となる自然数\(\mu_1,\mu_2\)を選びます。この添え字を基底とする項は、
\[\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m(\delta^{\mu_1\mu_2}_{\nu_1\nu_2})^2\omega_{\nu_1\nu_2}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)\]
となります。基底の添え字が\(\mu_1,\mu_2\)を含まない場合は、クロネッカーのデルタが0になるのでこれで網羅できています。2乗してあるのは、\(\omega_{\mu_1\mu_2}\)に付与した交代性が失われないようにするためです。総和記号を展開すれば、
\[\omega_{\mu_1\mu_2}dx^{\mu_1}(\Box_1)dx^{\mu_2}(\Box_2)+\omega_{\mu_2\mu_1}dx^{\mu_2}(\Box_1)dx^{\mu_1}(\Box_2)\]
正しいことが確認できると思います。\(\omega_{\nu_1\nu_2}\)の添え字とクロネッカーのデルタの片方の下付き添え字を\(\mu_1\mu_2\)に並び替えます。
\[\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m(\delta^{\mu_1\mu_2}_{\nu_1\nu_2})^2\omega_{\nu_1\nu_2}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)\]
\[=\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m\delta^{\mu_1\mu_2}_{\nu_1\nu_2}\delta^{\mu_1\mu_2}_{\mu_1\mu_2}\omega_{\mu_1\mu_2}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)\]
クロネッカーのデルタ、\(\omega_{\mu_1\mu_2}\)どちらも交代性があり、符号は変わらず統合が成り立ちます。
\[=\omega_{\mu_1\mu_2}\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m\delta^{\mu_1\mu_2}_{\nu_1\nu_2}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)\]
2次微分形式の基底が出てきましたね。
\[=\omega_{\mu_1\mu_2}dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)\]
今特定の\(\mu_1\lt\mu_2\in(1,2,\cdots,m)\)についてやりましたが、すべての\(\mu_1,\mu_2\)について、同様のことをすれば、
\[\omega(\Box_1,\Box_2)=\sum_{1\lt\mu_1\lt\mu_2\lt m}\omega_{\mu_1\mu_2}dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)\]
これがよく教本に載っている局所座標での微分形式です。\(\mu_1=\mu_2\)の項は\(\omega_{\mu_1\mu_2}\)の交代性から0になるので、考えなくていいです。接ベクトルが2つ代入できることは分かり切っているので、ほとんどの教本では\((\Box_1,\Box_2)\)は省略しています。例えば3次元多様体で2次微分形式は局所座標を用いて、
\[f(x,y,z)dx\wedge dy+g(x,y,z)dx\wedge dz+h(x,y,z)dy\wedge dz\]
などと3つの関数と3つの基底を用いて表されます。\(m\)次元多様体の\(k\)形式の基底は、\(_mC_k\)個あります。\(U_1\cap U_2\neq\varnothing\)であるチャート、\(\varphi_1(U_1\cap U_2)=(x^1,\cdots,x^m)\)、\(\varphi_2(U_1\cap U_2)=(y^1,\cdots,y^m)\)について、\(U_1\cap U_2\neq\varnothing\)上の微分形式が
\[\omega=\sum_{\mu_1\lt\mu_2}f_{\mu_1\mu_2}dx^{\mu_1}\wedge dx^{\mu_2}\]
\[\omega=\sum_{\nu_1\lt\nu_2}g_{\nu_1\nu_2}dy^{\nu_1}\wedge dy^{\nu_2}\]
と表される場合、2次微分形式の成分\(f_{ij}\)、基底ベクトル\(dx^i\wedge dx^j\)の座標変換がどのように行われるか見ていきます。1次微分形式の座標変換の定義
\[dx^i(\Box)=\sum_{j=1}^m\frac{\partial x^i}{\partial y^j}dy^j(\Box)\]
から2次微分形式の座標変換が自然に導かれます。
\[dx^{\mu_1}\wedge dx^{\mu_2}(\Box_1,\Box_2)=\sum_{\rho_1=1}^m\sum_{\rho_2=1}^m\delta^{\rho_1\rho_2}_{12}dx^{\mu_1}(\Box_{\rho_1})dx^{\mu_2}(\Box_{\rho_2})\]
\[=\sum_{\rho_1=1}^m\sum_{\rho_2=1}^m\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\delta^{\rho_1\rho_2}_{12}\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}dy^{\lambda_1}(\Box_{\rho_1})dy^{\lambda_2}(\Box_{\rho_2})\]
\[=\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}\sum_{\rho_1=1}^m\sum_{\rho_2=1}^m\delta^{\rho_1\rho_2}_{12}dy^{\lambda_1}(\Box_{\rho_1})dy^{\lambda_2}(\Box_{\rho_2})\]
\[=\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}dy^{\lambda_1}\wedge dy^{\lambda_2}(\Box_1,\Box_2)\]
2次微分形式の基底は添え字の小さい順に並べなくてはなりません。2つの自然数\(\nu_1,\nu_2\in(1,\cdots,m)\)が、\(\nu_1\lt\nu_2\)であったとしましょう。この2つの添え字を基底とする項は、
\[\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m(\delta_{\nu_1\nu_2}^{\lambda_1\lambda_2})^2\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}dy^{\lambda_1}\wedge dy^{\lambda_2}(\Box_1,\Box_2)\]
この2項です。\(m\)の2乗個あるように見えますが、クロネッカーのデルタのおかげで、\(\nu_1,\nu_2\)を添え字とする2項だけ残ります。2次微分形式の基底を\(dy^{\nu_1}\wedge dy^{\nu_2}\)に並び替えます。それと同時にクロネッカーのデルタの片方だけ下付き添え字を同じように並び替えます。符号が変化しないので、
\[=\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\delta_{\nu_1\nu_2}^{\lambda_1\lambda_2}\delta^{\nu_1\nu_2}_{\nu_1\nu_2}\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}dy^{\nu_1}\wedge dy^{\nu_2}(\Box_1,\Box_2)\]
\[=\left(\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\delta_{\nu_1\nu_2}^{\lambda_1\lambda_2}\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}\right)dy^{\nu_1}\wedge dy^{\nu_2}(\Box_1,\Box_2)\]
係数部分が、ヤコビアン
\[\frac{\partial(x^{\mu_1},x^{\mu_2})}{\partial(y^{\nu_1},y^{\nu_2})}=\sum_{\lambda_1=1}^m\sum_{\lambda_2=1}^m\delta_{\nu_1\nu_2}^{\lambda_1\lambda_2}\frac{\partial x^{\mu_1}}{\partial y^{\lambda_1}}\frac{\partial x^{\mu_2}}{\partial y^{\lambda_2}}\]
になっています。いま特定の\(\nu_1\lt\nu_2\)についてみてきましたが、すべての\(\nu_1\lt\nu_2\in(1,\cdots,m)\)について、同じことをして和を取れば、
\[dx^{\mu_1}\wedge dx^{\mu_2}=\sum_{\nu_1\lt\nu_2}\frac{\partial(x^{\mu_1},x^{\mu_2})}{\partial(y^{\nu_1},y^{\nu_2})}dy^{\nu_1}\wedge dy^{\nu_2}\]
また基底の変換から2次微分形式の座標変換は、
\[\omega=\sum_{\mu_1\lt\mu_2}f_{\mu_1\mu_2}dx^{\mu_1}\wedge dx^{\mu_2}\]
\[=\sum_{\nu_1\lt\nu_2}\sum_{\mu_1\lt\mu_2}f_{\mu_1\mu_2}\frac{\partial(x^{\mu_1},x^{\mu_2})}{\partial(y^{\nu_1},y^{\nu_2})}dy^{\nu_1}\wedge dy^{\nu_2}\]
\[=\sum_{\nu_1\lt\nu_2}g_{\nu_1\nu_2}dy^{\nu_1}\wedge dy^{\nu_2}\]
から2次微分形式の成分は、
\[g_{\nu_1\nu_2}=\sum_{\mu_1\lt\mu_2}f_{\mu_1\mu_2}\frac{\partial(x^{\mu_1},x^{\mu_2})}{\partial(y^{\nu_1},y^{\nu_2})}\]
どのような座標変換がなされるかが分かりましたね。どのような座標変換がなされるかも大切ですが、座標変換が存在することが示せたことが大きいです。チャート上での微分形式の定義が特定のチャートでなくても座標変換によりどの座標でも同じ定義になっています。よい定義というが確認できました。
2次微分形式の積分
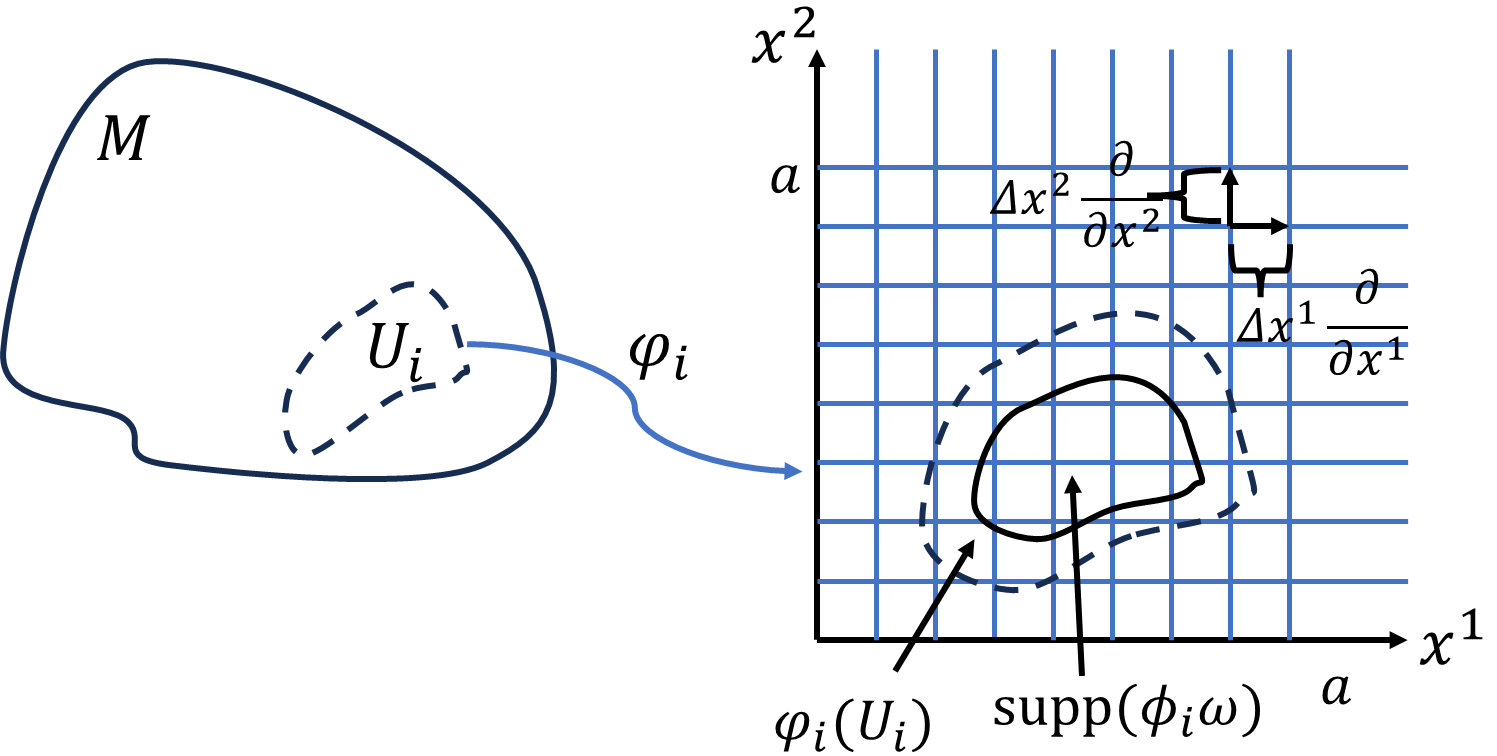
コンパクトで向き付け可能な(向き付け可能は後で解説)2次元多様体\(M\)のチャート、1の分割を\((\varphi_i,U_i,\phi_i)\)とします。また局所座標を\(\varphi_i=(x^1,x^2)\)と表すことにします。簡単にするため\(\varphi_i(U_i)\subset[0,a]\times[0,a]\)とします。そうならない場合は、\((x^1,x^2)\mapsto(x^1-u^1,x^2-u^2)\)と平行移動した、写像を局所座標と定義しなおして、\(\varphi_i(U_i)\)が第1象限に来るようにします。1辺が\(a\)の正方領域から、\(\varphi_i(U_i)\)がはみ出るなら、もっと\(a\)を大きく取りましょう。局所座標に写した開集合は、\(U_i\)上の任意の点\(p\)で
\[\varDelta \vec{x}^1_\rho=\varDelta x^1_\rho\frac{\partial}{\partial x^1},\ \varDelta \vec{x}^2_\lambda=\varDelta x^2_\lambda\frac{\partial}{\partial x^2}\]
という線素ベクトルを取ります。\(\varDelta x^1_\rho=x^1_\rho-x^1_{\rho-1},\ 0=x^1_0\lt x^1_1\lt x^1_2\lt\cdots\lt x^1_n=a\)、\(\varDelta x^2_\lambda=x^2_\lambda-x^2_{\lambda-1},\ 0=x^2_0\lt x^2_1\lt x^2_2\lt\cdots\lt x^2_n=a\)とベクトルの係数は決まっています。\([0,a]\times[0,a]\)の点\((x_\rho,x_\lambda)\)を始点として、\(n^2\)個の線素ベクトルがあるようにします。多様体\(M\)上は2次元多様体なので、2次微分形式\(\omega\)は、局所座標で
\[\omega=\omega_{12}dx^1\wedge dx^2\]
となります。\(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda\)を代入すれば、
\[\omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)=\omega_{12}dx^1(\varDelta \vec{x}^1_\rho)dx^2(\varDelta \vec{x}^2_\lambda)-\omega_{12}dx^2(\varDelta \vec{x}^1_\rho)dx^1(\varDelta \vec{x}^2_\lambda)\]
\[\omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)=\omega_{12}\varDelta x^1_\rho\varDelta x^2_\lambda\]
つまり\(\omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)\)を図形的に解釈すると、底辺\(\varDelta x^1_\rho\varDelta x^2_\lambda\)の長方形、高さが\(\omega_{12}\)の立方体となります。この細長い立方体となります。底辺を0に近づける極限で積分と一致します。
\[\int_{U_i}\omega=\sum_{(x^1_\rho,x^2_\lambda)\in\varphi_i(U_i)}\omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)=\int_{\varphi_i(U_i)}\omega_{12}dx^1dx^2\]
\(\rho,\lambda\)を0から\(n\)まで足し合わせると、\(\varphi_i(U_i)\)での積分値でなく、\([0,a]\times[0,a]\)でのリーマン和になってしまいます。しかし、\(\varphi_i(U_i)\)の部分だけの細長い長方形の体積の総和を取るのは面倒です。ここで輝くのが1の分割\(\phi_i\)です。\(\mathrm{supp}(\phi_i\circ\varphi_i^{-1}(x^1,x^2))\subset\varphi_i(U_i)\)一の分割は、\(U_i\)の外では0、局所座標に持ち込んでも\(\phi_i\circ\varphi_i^{-1}\)は、\(\varphi_i(U_i)\)の外で0です。これを微分形式にかけることで、\(\mathrm{supp}(\phi_i\omega)\subset U_i\)、なぜそのように言えるかというと、微分形式は、多様体全体で値を持つかもしれませんが、\(\phi_i\)は\(U_i\)の外で0、微分形式が値を持っていても0をかけることで0となるのです。
\[\int_{U_i}\phi_i\omega=\sum_{\rho=1}^n\sum_{\lambda=1}^n\phi_i\circ\varphi_i^{-1}(x^1_\rho,x^2_\lambda)\ \omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)\]
1の分割をかけてから積分することで、\(\varphi_i(U_i)\)の外で細長い長方形の高さが0になる為、正方領域\([0,a]\times[0,a]\)でのリーマン和とも等しいです。
\[\int_{U_i}\phi_i\omega=\sum_{\rho=1}^n\sum_{\lambda=1}^n\phi_i\circ\varphi_i^{-1}(x^1_\rho,x^2_\lambda)\ \omega(\varDelta \vec{x}^1_\rho,\varDelta \vec{x}^2_\lambda)\]
\[\int_{U_i}\phi_i\omega=\int_0^a\int_0^a\phi_i\circ\varphi_i^{-1}\omega_{12} dx^1dx^2\]
積分範囲も同様に正方領域になり、計算がだいぶ楽になりますね。後でストークスの定理で使用します。これで2次元多様体の2次微分形式の積分
\[\int_M\omega=\sum_{i=1}^k\int_{U_i}\phi_i\omega\]
が完成!といいたいとことですが、向き付け可能ということも確認せねばなりません。2次微分形式の座標変換についてみてみましょう。\(U_i\cap U_j\neq\varnothing\)となる開被覆\(U_j\)の局所座標を\(\varphi_j=(y^1,y^2)\)とします。2次元多様体上の任意の点\(p\in U_i\cap U_j\)について、微分形式は、
\[\omega_{12}dx^1\wedge dx^2=\frac{\partial(x^1,x^2)}{\partial(y^1,y^2)}\omega_{12}dy^1\wedge dy^2\]
と変換されます。以下ヤコビアンを\(J\)と書きます。\(\omega_{12}\)は\((x^1,x^2)\)の関数で、\(\omega\circ\varphi_i\circ\varphi_j^{-1}(y^1,y^2)\)と書くべきですが、長いので省略します。\(\varphi_j\)にも差分ベクトル
\[\varDelta\vec{y}^1_p=(y^l_{p}-y^1_{p-1})\frac{\partial }{\partial y^1}\]
\[\varDelta\vec{y}^2_q=(y^2_{q}-y^2_{q-1})\frac{\partial }{\partial y^2}\]
を定義することで、
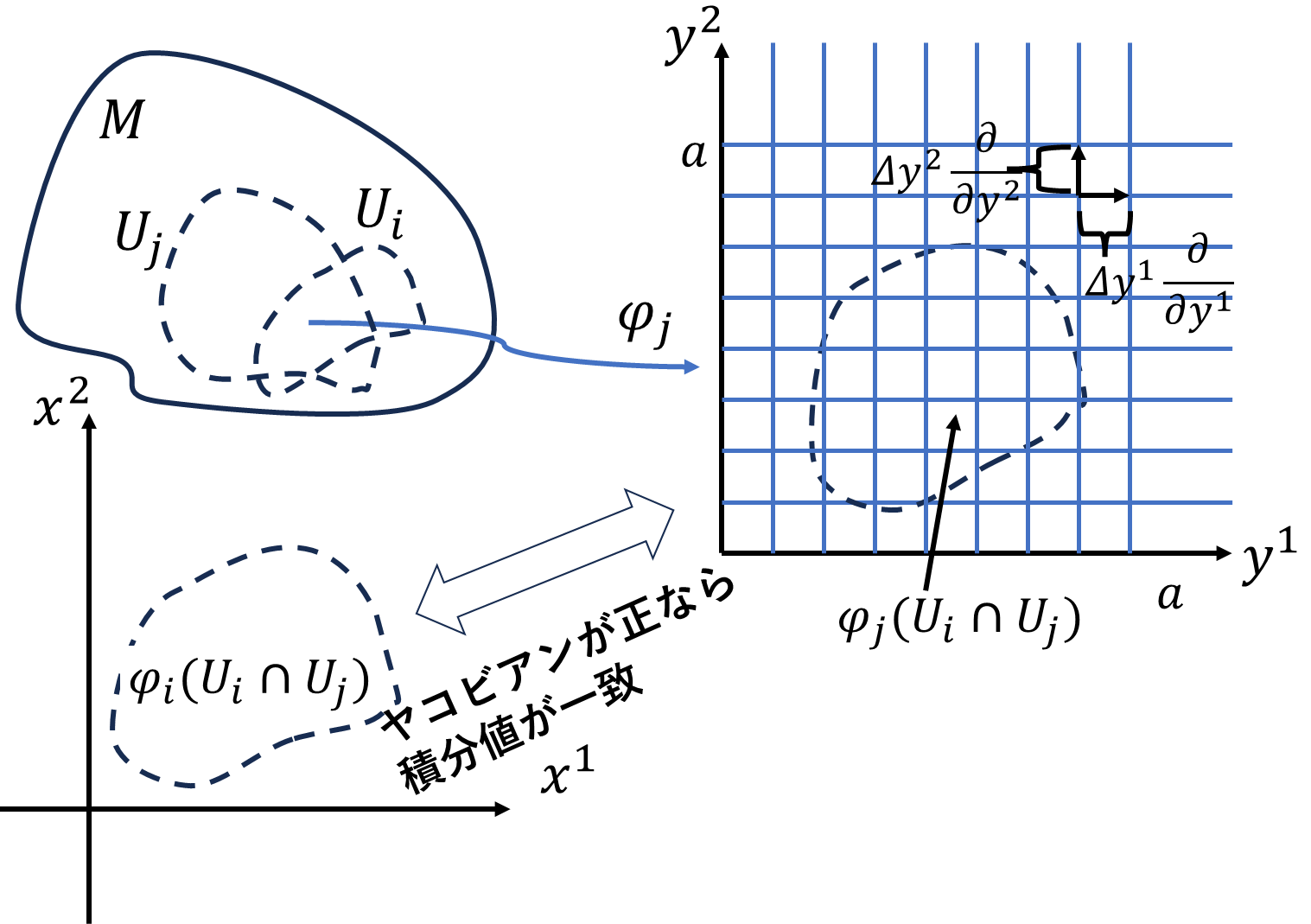
リーマン和を考えることができます。
\[\int_{U_i\cap U_j}\omega=\int_{\varphi_j(U_i\cap U_j)}J\omega_{12}dy^1dy^2\]
\[=\sum_{(y^1_p,y^2_q)\in\varphi_j(U_i\cap U_j)}J\omega_{12}dy^1\wedge dy^2(\varDelta\vec{y}^1_p,\varDelta\vec{y}^2_q)\]
\[=\sum_{(y^1_p,y^2_q)\in\varphi_j(U_i\cap U_j)}J\omega_{12}\varDelta y^1_p\varDelta y^2_q\]
\[=\sum_{(y^1_p,y^2_q)\in\varphi_j(U_i\cap U_j)}|J|\omega_{12}(\pm\varDelta y^1_p\varDelta y^2_q)\]
このように、もともとの局所座標\(\varphi_i=(x^1,x^2)\)でのリーマン和は
\[\int_{U_i\cap U_j}\omega=\sum_{(y^1_\rho,y^2_\lambda)\in\varphi_j(U_i\cap U_j)}\omega_{12}\varDelta x^1_\rho\varDelta x^2_\lambda\]
\(\omega_{12}\)と、\(|J|\omega_{12}\)の符号は一致しているので、リーマン和をなす細長い立方体の高さは2つの座標で符号が一致しています。つまり2つの座標で積分値が等しくなるためには、直方体の底面積\(\pm\varDelta y^1\varDelta y^2\)が\(+\)の符号を取る必要があります。これは座標変換のヤコビアンが多様体上でどこでも正である必要があることと同値(同等の条件)です。2形式の成分でも多様体上の座標変換が正になることが積分値を一意に決める条件になります。
\(3\)次微分形式
m次元多様体上のベクトル場\(X_1,X_2,X_3\)をある局所座標\(\varphi_i=(x^1,x^2,\cdots,x^m)\)で
\[X_j=\sum_{i=1}^mX_j^i\frac{\partial}{\partial x^i}\quad(j=1,2,3)\]
と表せるとします。
写像\(f:(X_1,X_2,X_3)\mapsto\mathbb{R}\)が線形性を持つ場合、写像は局所座標で、
\[f(X_1,X_2,X_3)=\sum_{i_1=1}^m\sum_{i_2=1}^m\sum_{i_3=1}^mf_{i_1i_2i_3}X^{i_1}_1X^{i_2}_2X^{i_3}_3\]
の形に限定されます。\(f_{i_1i_2i_3}:(x^1,x^2,x^3)\mapsto\mathbb{R}\)はチャート上の関数です。これから総和記号がたくさん出てきますが、複雑になりますので、
\[f(X_1,X_2,X_3)=f_{i_1i_2i_3}X^{i_1}_1X^{i_2}_2X^{i_3}_3\]
文脈で判断できると思われる場合は省略します。2次微分形式を理解できたなら大丈夫だと思います。1次微分形式の基底を用いることで、この写像は、ベクトル場無しで記述されます。
\[f(\Box_1,\Box_2,\Box_3)=f_{i_1i_2i_3}dx^{i_1}(\Box_1)dx^{i_2}(\Box_2)dx^{i_3}(\Box_3)\]
\(\Box\)の部分にベクトル場を代入できます。微分形式の条件(ii)の交代性も満たすために関数\(f_{i_1i_2i_3}:(x^1,x^2,x^3)\mapsto\mathbb{R}\)に制限を加えます。任意の関数\(g_{j_1j_2j_3}:(x^1,x^2,x^3)\mapsto\mathbb{R}\)を用いて、
\[f_{i_1i_2i_3}=\sum_{j_1=1}^m\sum_{j_2=1}^m\sum_{j_3=1}^m\delta_{i_1i_2i_3}^{j_1j_2j_3}g_{j_1j_2j_3}\]
とします。例えば\(i_1\)と\(i_3\)を交換すれば、クロネッカーのデルタのおかげで符号が反転するようになりました。
\[f_{i_3i_2i_1}=\delta_{i_3i_2i_1}^{j_1j_2j_3}g_{j_1j_2j_3}=-\delta_{i_1i_2i_3}^{j_1j_2j_3}g_{j_1j_2j_3}=-f_{i_1i_2i_3}\]
交代性を有しているということです。\(f_{i_3i_2i_1}\)が交代性を有していれば、
\[f(Z,Y,X)=f_{i_1i_2i_3}dx^{i_1}(Z)dx^{i_2}(Y)dx^{i_3}(X)\]
\[=-f_{i_3i_2i_1}dx^{i_3}(X)dx^{i_2}(Y)dx^{i_1}(Z)=-f(X,Y,Z)\]
今\(X,Z\)にしか確認しませんでしたがどのベクトルを交換しても交代性を示すようにできています。\(i_3\)と\(i_1\)の添え字も順番が変わっていることが気になるかもしれませんが、ダミーの添え字なので大丈夫です。(総和記号を使うために導入された添え字で、元の写像\(f\)に関係ない。)写像\(f:(X_1,X_2,X_3)\mapsto\mathbb{R}\)に交代性を持たせることができました。\(f_{i_3i_2i_1}\)をなめらかにしたものが3次微分形式ですが、3次微分形式には専用の基底
\[dx^{\mu_1}\wedge dx^{\mu_2}\wedge dx^{\mu_3}(\Box_1,\Box_2,\Box_3)\]
\[=\sum_{\rho_1=1}^m\sum_{\rho_2=1}^m\sum_{\rho_3=1}^m\delta^{\rho_1\rho_2\rho_3}_{1\ \ 2\ \ 3}dx^{\mu_1}(\Box_{\rho_1})dx^{\mu_2}(\Box_{\rho_2})dx^{\mu_3}(\Box_{\rho_3})\]
\[=\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m\sum_{\nu_3=1}^m\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)dx^{\nu_3}(\Box_3)\]
がありますので、それを使います。ただし、\(\mu_1\lt\mu_2\lt\mu_3\)です。初めに3の自然数\(\mu_1\lt\mu_2\lt\mu_3\in(1,\cdots,m)\)を選んで、
\[f(\Box_1,\Box_2,\Box_3)=f_{i_1i_2i_3}dx^{i_1}(\Box_1)dx^{i_2}(\Box_2)dx^{i_3}(\Box_3)\]
の中からこの3つの自然数を添え字に持つ項のみを足していきます。
\[\sum_{\nu_1=1}^m\sum_{\nu_2=1}^m\sum_{\nu_3=1}^m(\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3})^2f_{\nu_1\nu_2\nu_3}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)dx^{\nu_3}(\Box_3)\]
\(\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3}\)のおかげで、\(\mu_1\mu_2\mu_3\)の並び替えの項しか出てきません。2乗しているのは、\(f_{\nu_1\nu_2\nu_3}\)に付与した交代性が、クロネッカーのデルタで消えないようにするためです。\(f_{\nu_1\nu_2\nu_3}\)の添え字を並び替えます。同時に\(\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3}\)の片方だけ下の添え字も並び替えます。
\[=\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3}\delta^{\mu_1\mu_2\mu_3}_{\mu_1\mu_2\mu_3}f_{\mu_1\mu_2\mu_3}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)dx^{\nu_3}(\Box_3)\]
\[=f_{\mu_1\mu_2\mu_3}\delta^{\mu_1\mu_2\mu_3}_{\nu_1\nu_2\nu_3}dx^{\nu_1}(\Box_1)dx^{\nu_2}(\Box_2)dx^{\nu_3}(\Box_3)\]
これをすべての\(\mu_1,\mu_2,\mu_3\)について行いその総和を取れば、
\[f(\Box_1,\Box_2,\Box_3)=\sum_{\mu_1\lt\mu_2\lt\mu_3}f_{\mu_1\mu_2\mu_3}dx^{\mu_1}\wedge dx^{\mu_2}\wedge dx^{\mu_3}(\Box_1,\Box_2,\Box_3)\]
これが3次微分形式の正体です。この定義がチャート上の定義として、良い定義かどうかは\(k\)形式の時に示します。
\(3\)次微分形式の積分
向き付け可能でコンパクトな3次元多様体\(M\)上で、チャート、1の分割の組を\((\varphi_i,U_i,\phi_i)\)とします。局所座標は、\(\varphi_i=(x^1,x^2,x^3)\)と表すことにします。\(\varphi_i(U_i)\)が、\(x^1,x^2,x^3\ge0\)の領域に収まるように同相写像\(\varphi_i\)は工夫します。局所座標\(\varphi_i=(x^1,x^2,x^3)\)上では、
3次微分形式\(\omega\)は、
\[\omega(\Box_1,\Box_2,\Box_3)=\omega_{123}dx^1\wedge dx^2\wedge dx^3(\Box_1,\Box_2,\Box_3)\]
となります。\(\Box\)には接ベクトルを代入できて、3つ代入すれば1つのスカラー値が得られます。3次微分形式の共通部分を持つチャートでの座標変換を見てみます。
\[dx^1\wedge dx^2\wedge dx^3(\Box_1,\Box_2,\Box_3)\]
\[=\epsilon_{123}^{\rho_1\rho_2\rho_3}dx^{1}(\Box_{\rho_1})dx^2(\Box_{\rho_2})dx^3(\Box_{\rho_3})\]
\[=\epsilon_{123}^{\rho_1\rho_2\rho_3}\frac{\partial x^1}{\partial y^{\lambda_1}}dy^{\lambda_1}(\Box_{\rho_1})\frac{\partial x^1}{\partial y^{\lambda_2}}dy^{\lambda_2}(\Box_{\rho_2})\frac{\partial x^1}{\partial y^{\lambda_3}}dy^{\lambda_3}(\Box_{\rho_3})\]
\[=\frac{\partial x^1}{\partial y^{\lambda_1}}\frac{\partial x^1}{\partial y^{\lambda_2}}\frac{\partial x^1}{\partial y^{\lambda_3}}\epsilon_{123}^{\rho_1\rho_2\rho_3}dy^{\lambda_1}(\Box_{\rho_1})dy^{\lambda_2}(\Box_{\rho_2})dy^{\lambda_3}(\Box_{\rho_3})\]
\[=\frac{\partial x^1}{\partial y^{\lambda_1}}\frac{\partial x^1}{\partial y^{\lambda_2}}\frac{\partial x^1}{\partial y^{\lambda_3}}dy^{\lambda_1}\wedge dy^{\lambda_2}\wedge dy^{\lambda_3}(\Box_1,\Box_2,\Box_3)\]
微分形式の基底は添え字が小さい順に並び替えなければならないので、基底の添え字\(\lambda_1,\lambda_2,\lambda_3\)を\(1,2,3\)に並び替えます。それにより、符号\(\delta^{123}_{\lambda_1\lambda_2\lambda_3}\)が出てきます。
\[=\delta^{123}_{\lambda_1\lambda_2\lambda_3}\frac{\partial x^1}{\partial y^{\lambda_1}}\frac{\partial x^1}{\partial y^{\lambda_2}}\frac{\partial x^1}{\partial y^{\lambda_3}}dy^1\wedge dy^2\wedge dy^3(\Box_1,\Box_2,\Box_3)\]
\[=\frac{\partial (x^1,x^2,x^3)}{\partial (y^1,y^2,y^3)}dy^1\wedge dy^2\wedge dy^3(\Box_1,\Box_2,\Box_3)\]
自然にヤコビアンが出てきます。
\(\varphi_i(U_i)\)上で差分ベクトル
\[\varDelta \vec{x}^\lambda_{\rho}:=\varDelta x^\lambda_\rho\frac{\partial}{\partial x^\lambda}\]
を定義します。ただし、
\[\varDelta x^\lambda_\rho=x^\lambda_{\rho}-x^\lambda_{\rho-1},\ 0=x^\lambda_{0}\lt x^\lambda_{1}\lt\cdots\lt x^\lambda_{n}=a\]
です。\(a\)を十分大きく取れば、開被覆の同相写像を1辺\(a\)の立方領域で覆うことができます。\(\varphi_i(U_i)\subset[0,a]\times[0,a]\times[0,a]\)

この図は2次元の時の流用ですが、イメージは全く同じです。各軸に平行な差分ベクトルを3次微分形式に代入します。本当は1の分割は多様体上の関数で、座標を用いて表す場合は、\(\phi_i\circ\varphi^{-1}_i(x^1,x^2,x^3)\)とするべきですが、単に\(\phi_i\)と書きます。
\[\phi_i\omega(\varDelta \vec{x}^1_{\rho_1},\varDelta \vec{x}^2_{\rho_2},\varDelta \vec{x}^3_{\rho_3})=\phi_i\omega_{123}\varDelta x^1_{\rho_1}\varDelta x^2_{\rho_2}\varDelta x^3_{\rho_3}\]
であるので、\(\varDelta x^1_1\varDelta x^2_2\varDelta x^3_3\)を底辺、\(\phi_i\omega_{123}\)を高さとする細長い超直方体の体積となります。余接ベクトル\(dx^i\)はベクトルを実数に写す線形写像ですが、差分ベクトルを代入することで、微小量としての\(dx^i\)ともとらえることができますね。積分値は、
\[\int_{U_i}\phi_i\omega=\int_0^a\int_0^a\int_0^a\phi_i\omega_{123}dx^1dx^2dx^3\]
\[\simeq\sum_{\rho_1=1}^n\sum_{\rho_2=1}^n\sum_{\rho_3=1}^n\phi_i\omega_{123}\varDelta x^1_{\rho_1}\varDelta x^2_{\rho_2}\varDelta x^3_{\rho_3}\]
となります。リーマン和としても表すことができます。積分範囲やリーマン和を立方領域と広めにとっていますが、\(\mathrm{supp}(\phi_i\omega)\subset\varphi_i(U_i)\)なので少なくとも\(\varphi_i(U_i)\)の外で、細長い超直方体の高さ\(\phi_i\omega_{123}\)は0です。つまり、\(\varphi_i(U_i)\)の外でのリーマン和は積分の値に寄与しません。\(U_i\cap U_j\neq\varnothing\)である別の局所座標\(\varphi_j=(y^1,y^2,y^3)\)でも座標の向きが等しい必要もあります。つまり座標変換のヤコビアンが正
\[J=\frac{\partial(x^1,x^2,x^3)}{\partial(y^1,y^2,y^3)}\gt0\]
である必要があります。ヤコビアンが正を図形的に解釈したいなら、リーマン和の表記方が分かりやすいと思います。\(U_i\cap U_j\)での積分値は2つの局所座標で、
\[\int_{U_i\cap U_j}\omega\simeq\sum_{(x^1_{\rho_1},x^2_{\rho_2},x^3_{\rho_3})\in\varphi_i(U_i\cap U_j)}\omega_{123}\varDelta x^1_{\rho_1}\varDelta x^2_{\rho_2}\varDelta x^3_{\rho_3}\]
また\(\varphi_j\)の座標でのリーマン和は、
\[\int_{U_i\cap U_j}\omega\simeq\sum_{(y^1_{\rho_1},y^2_{\rho_2},y^3_{\rho_3})\in\varphi_j(U_i\cap U_j)}|J|\omega_{123}(\pm\varDelta y^1_{\rho_1}\varDelta y^2_{\rho_2}\varDelta y^3_{\rho_3})\]
開被覆の共通部分\(U_i\cap U_j\)において積分値が一致するためには、\(U_i\cap U_j\)のどの点においてもヤコビアン\(J=\pm|J|\)が正である必要があります。\(|J|\omega_{123}\)を高さとすれば、底面積の符号はヤコビアンによって決まります。2つの局所座標で底面積の符号が一致していれば、積分値が一致します。多様体上のすべての点で座標変換のヤコビアンが正にできる事を向き付け可能といい、そのようなチャートのみでアトラスを組んだコンパクトな多様体で、
\[\int_{M}\omega=\sum_{i=1}^k\int_{U_i}\phi_i\omega\]
積分が定義できるというわけです。


