楽しい科学(理論)チャンネル
ベクトル
今回もユークリッド空間で考えていきます。
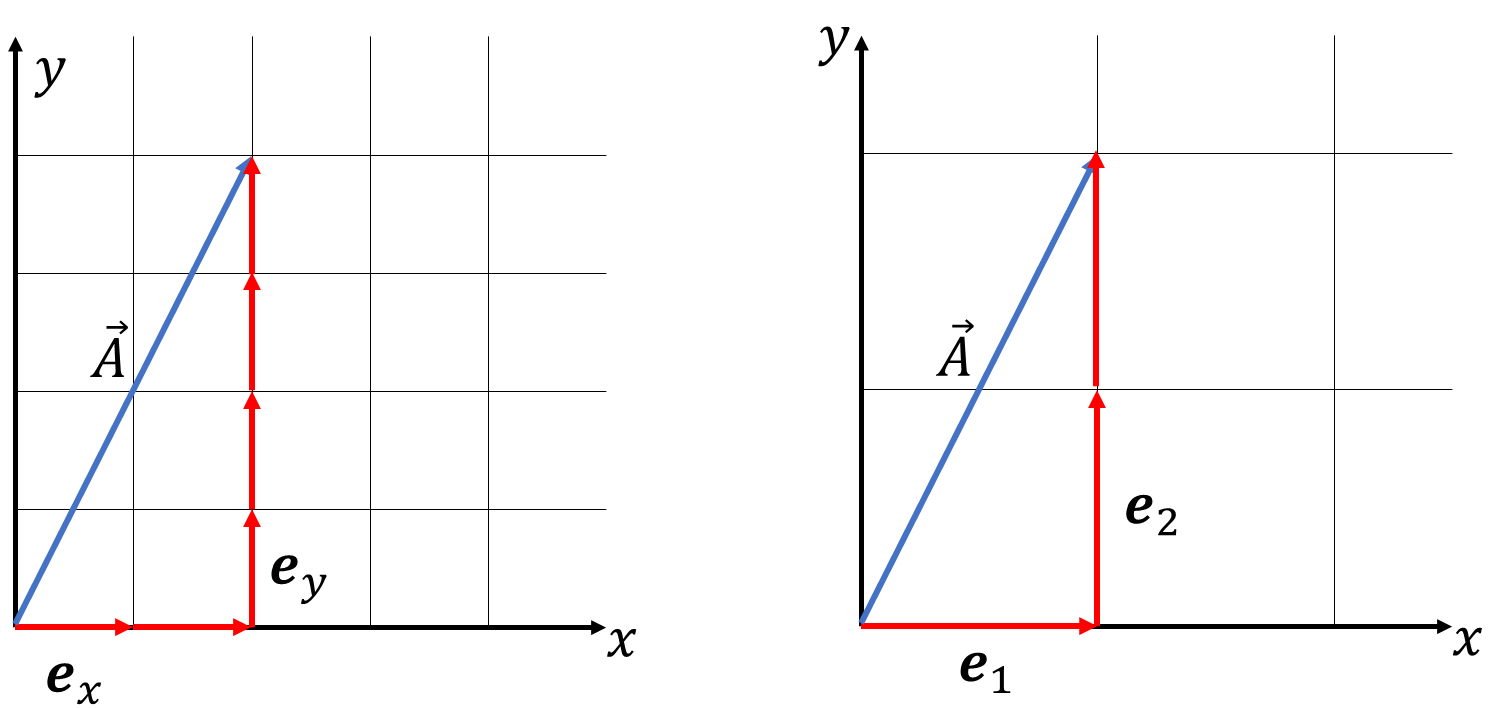
図のように2次元ユークリッド空間上の大きさと向きを持ったものをベクトルと定義します。ベクトル\(\vec{A}\)は原点から\(x\)軸方向に2、\(y\)方向に4進んだ点の位置を表すことができます。
\[\vec{A}:=(2,4)\]
さらに、\(x,y\)軸正の方向の大きさ1のベクトルを、標準基底と呼び、
\[\boldsymbol{e}_x=(1,0),\ \boldsymbol{e}_y=(0,1)\]
と表します。(説明を手早くするため、定義する前に基底という言葉を用いています。)これを使って、
\[\vec{A}=2\boldsymbol{e}_x+4\boldsymbol{e}_y\]
2次元ユークリッド空間の基底ベクトルは、標準基底だけではなく、
\[\boldsymbol{e}_1=(2,0),\ \boldsymbol{e}_2=(0,2)\]
も基底ベクトルとして扱えます。これらの基底ベクトルを用いて、
\[\vec{A}=\boldsymbol{e}_1+2\boldsymbol{e}_2\]
とも表すことができます。
\[\vec{A}=A^1e_1+A^2e_2=\sum_{i=1}^2A^ie_i\]
と表した時、基底ベクトルの係数\(A^1,A^2\)を\(\vec{A}\)成分と呼びます。もちろんこの成分は基底ベクトルに依存します。
ベクトルは矢印\(\vec{A}\)や太字\(\boldsymbol{A}\)で表す本が多いですが、これから多様体を勉強する読者のために大文字\(A\)でベクトルを表すことにします。矢印がない、太字じゃないからスカラーや関数だと思わないことが大切です。関数\(A\)と言われているのか、定数\(A\)と言われるのか、ベクトル\(A\)と言われるのか本に書いてあるのですがね。
ベクトルの計算
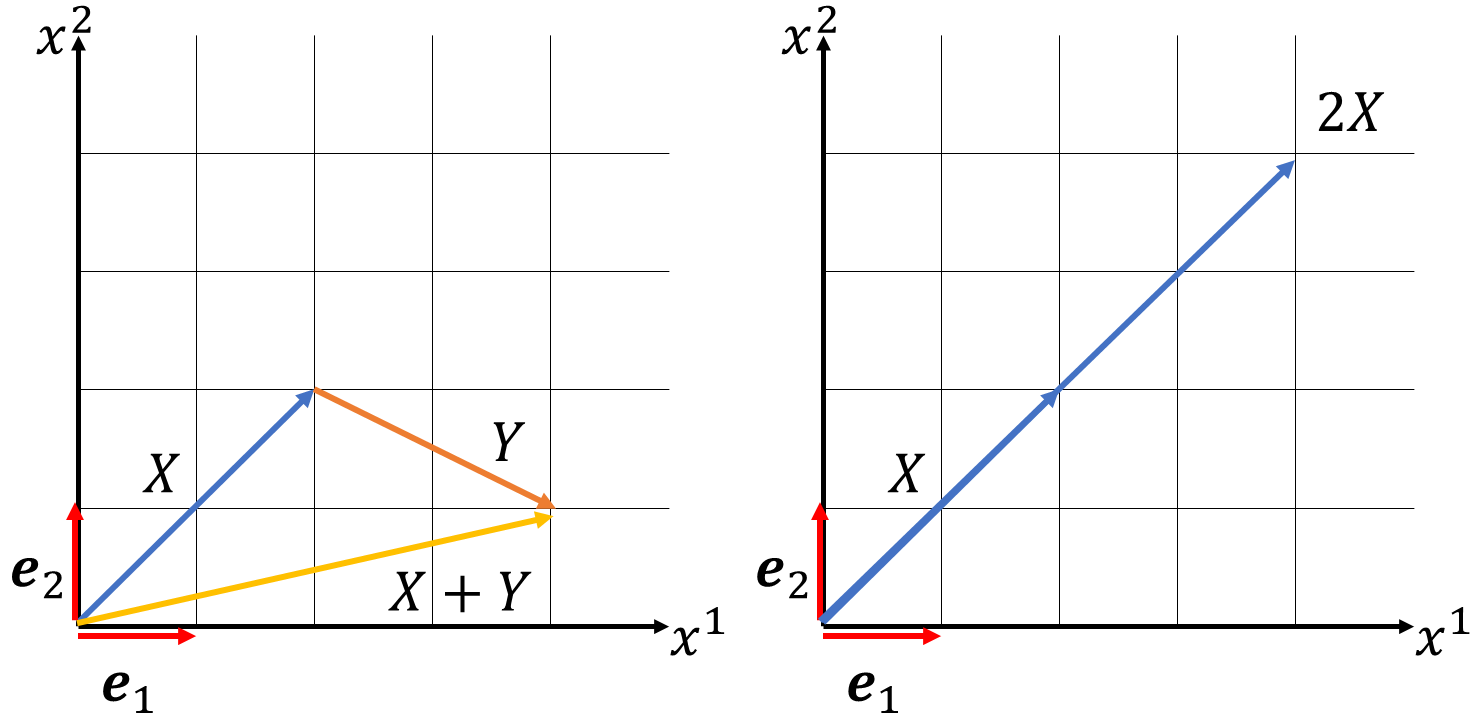
ベクトルの加法は図のように\(X\)進んで、\(Y\)進んだ位置を\(X+Y\)とすると覚えるとよいです。それがそのままベクトルの加法になります。スカラー倍は、\(X\)進んで、\(X\)進んだ位置を\(2X\)と表せばよいです。2つのベクトル
\[X=X^1e_1+X^2e_2,\ Y=Y^1e_1+Y^2e_2\]
について、ベクトルの加法、スカラー倍を以下のように定義します。ベクトルには、\(X=(X^1,X^2)\)のように、成分だけ並べて書く記法があります。
(i) 加法
\[X+ Y=(X^1+ Y^1,X^2+ Y^2)\]
(ii) スカラー倍
\[kX=(kX^1,kX^2)\]
このような計算ができます。
基底ベクトル
\(m\)次元ユークリッド空間\(\mathbb{R}^m\)上の任意のベクトル\(X\)を\(m\)個のベクトル\(\{e_1,\cdots,e_m\}\)を用いて、
\[X=X^1e_1+\cdots+X^me_m\]
と表すことができる実数\(X^1,\cdots,X^m\)が存在するとき、\(\{e_1,\cdots,e_m\}\)を基底ベクトルといいます。また実数\(X^1,\cdots,X^m\)を、\(\{e_1,\cdots,e_m\}\)を基底とする、ベクトル\(X\)の成分といいます。基底ベクトルの条件について考えていましょう。ベクトル空間上のベクトル2次元ユークリッド空間のベクトル\(X=(2,4)\)は基底ベクトル
\[v_1=(2,0),\ v_2=(1,1)\]
を用いて、
\[X=-(2,0)+(4,4)=-v_1+4v_2\]
などと表すことができます。
\[u_1=(1,1),u_2=(2,2)\]
では、\(X\)を表すことができません。
\[U^1u_1+U^2u_2=(U^1+2U^2,U^1+2U^2)\]
実数\(U^1,U^2\)の値をどれだけ工夫しても\(x,y\)の成分がいずれも同じ値になってしまいます。これは、\(u_1,u_2\)が平行である為、\(u_1\)方向の基底ベクトルと同じ方向のベクトルしか表現できないためです。3次元空間の例だと
\[e_1=(1,0,0),\ e_2=(1,0,1)\ e_3=(3,0,1)\]
は基底ベクトルの条件を満たしません。3つの基底ベクトルは平行ではありません。しかし、
\[e_3=e_1+2e_2\]
であるため、
\[X=X^1e_1+X^2e_2+X^3e_3=2X^1e_1+3X^2e_2\]
ベクトル\(e_1,e_2\)を含む平面上のベクトルしか表せないので、3次元空間の基底ベクトルとは言えません。
\(m\)次元空間の基底ベクトルである条件は、
\[k_1e_1+\cdots+k_me_m=\vec{0}\ \implies\ k_1=\cdots=k_m=0\]
です。この条件を一次独立といいます。基底ベクトルの線形結合(各、基底ベクトルの定数倍の和)が\(\vec{0}\)になるならば、すべての係数は0となる。ということです。これでは意味が分かりにくいという方は、
\[\forall i\in(1,\cdots,m),\ \forall K_i\in\mathbb{R}:\quad e_i\neq K_1e_1+\cdots+\mathop{K_ie_i}^{\times}+\cdots+K_me_m\]
と覚えてもいいでしょう。\(\mathop{K_ie_i}^{\times}\)はこの項がないことを意味します。元の式より若干複雑になってしまいました。しかし、一次独立と基底ベクトルの満たしてほしい関係が明確化と思います。この式の意味は、任意の\(i\in(1,\cdots,m),\ K_i\in\mathbb{R}\)について、基底ベクトルがほかの基底ベクトルの線形結合で表せないという意味です。仮に\(e_i\)の線形結合で表せてしまった場合は、\(e_i\)を除く基底ベクトルで、\(\mathbb{R}^{m-1}\)次元空間のベクトルしか基底ベクトルの線形結合で表現できないことになります。
総和記号の公式
ちょっとした補足説明です。これから総和記号をたくさん使うのでその公式集です。
\[\sum_{i=1}^ma_i=\sum_{\mu=1}^ma_\mu\]
**ダミーの添え字 証明**
\[\sum_{i=1}^ma_i=a_1+a_2+\cdots+a_m=\sum_{\mu=1}^ma_\mu\]
終わり
\[\left(\sum_{i=1}^ma_i\right)\left(\sum_{j=1}^nb_j\right)=\sum_{i=1}^m\sum_{j=1}^na_ib_j\]
**総和の積その1 証明**
\[\left(\sum_{i=1}^ma_i\right)\left(\sum_{j=1}^nb_j\right)=(a_1+\cdots a_m)(b_1+\cdots+b_n)\]
\[\begin{matrix}=a_1b_1+a_1b_2+\cdots+a_1b_n\\
+a_2b_1+a_2b_2+\cdots+a_2b_n\\
\cdots\\
+a_mb_1+a_mb_2+\cdots+a_mb_n\end{matrix}\]
\[=\sum_{j=1}^na_1b_j+\sum_{j=1}^na_2b_j\cdots+\sum_{j=1}^na_mb_j\]
\[=\sum_{i=1}^m\sum_{j=1}^na_ib_j\]
**終わり**
\[\left(\sum_{i=1}^ma_i\left(\sum_{j=1}^nb_j\right)\right)=\sum_{i=1}^m\sum_{j=1}^na_ib_j\]
**総和の積その2 証明**
\[\left(\sum_{i=1}^ma_i\left(\sum_{j=1}^nb_j\right)\right)=a_1\left(\sum_{j=1}^nb_j\right)+\cdots a_m\left(\sum_{j=1}^nb_j\right)\]
\[\begin{matrix}=a_1b_1+a_1b_2+\cdots+a_1b_n\\
+a_2b_1+a_2b_2+\cdots+a_2b_n\\
\cdots\\
+a_mb_1+a_mb_2+\cdots+a_mb_n\end{matrix}\]
\[=\sum_{j=1}^na_1b_j+\sum_{j=1}^na_2b_j\cdots+\sum_{j=1}^na_mb_j\]
\[=\sum_{i=1}^m\sum_{j=1}^na_ib_j\]
**終わり**
\[\sum_{i=1}^m\sum_{j=1}^nc_{ij}=\sum_{j=1}^n\sum_{i=1}^mc_{ij}\]
**総和の交換法則 証明**
\[\sum_{i=1}^m\sum_{j=1}^nc_{ij}\]
\[\begin{matrix}=c_{11}+c_{12}+\cdots+c_{1n}\\
+c_{21}+c_{22}+\cdots+c_{2n}\\
\cdots\\
+c_{m1}+c_{m2}+\cdots+c_{mn}\end{matrix}\]
\(c_{11}+c_{21}+\cdots\)みたいに縦で足していきます。
\[=\sum_{i=1}^mc_{i1}+\sum_{i=1}^mc_{i2}\cdots+\sum_{i=1}^mc_{in}=\sum_{j=1}^n\sum_{i=1}^mc_{ij}\]
**終わり**
ダミーの添え字だけ公式の名前があって、ほかは私が勝手に名前を付けました。
行列
ベクトルの成分の組\(X=(X^1,X^2,X^3)\)、\(Y=(Y^1,Y^2,Y^3)\)について、
\[\begin{cases}
Y^1=a^1_{\ 1}X^1+a^1_{\ 2}X^2+a^1_{\ 3}X^3
\\Y^2=a^2_{\ 1}X^1+a^2_{\ 2}X^2+a^2_{\ 3}X^3
\\Y^3=a^3_{\ 1}X^1+a^3_{\ 2}X^2+a^3_{\ 3}X^3
\end{cases}\]
という連立方程式があったとしましょう。\(a^i_{\ j}\)は定数です。定数は\(a,b,c\cdots\)とすると文字をたくさん使ってしまうので、通し番号を振ることにします。\(i\)番目を取り出して
\[Y^i=a^i_{\ 1}X^1+a^i_{\ 2}X^2+a^i_3X^3\ (i=1,2,3)\]
\[Y^i=\sum_{j=1}^3a^i_{\ j}X^j\]
連立方程式の係数部分だけを抜き出したものを行列\((a^i_{\ j})\)と呼ぶことにしましょう。
\[(a^i_{\ j}):=\begin{pmatrix}
a^1_{\ 1}&a^1_{\ 2}&a^1_{\ 3}
\\a^2_{\ 1}&a^2_{\ 2}&a^2_{\ 3}
\\a^3_{\ 1}&a^3_{\ 2}&a^3_{\ 3}
\end{pmatrix}\]
ベクトル\(X\)と、行列\((a^i_j)\)の積を
\[\begin{pmatrix}
a^1_{\ 1}&a^1_{\ 2}&a^1_{\ 3}
\\a^2_{\ 1}&a^2_{\ 2}&a^2_{\ 3}
\\a^3_{\ 1}&a^3_{\ 2}&a^3_{\ 3}
\end{pmatrix}
\begin{pmatrix}
X^1
\\X^2
\\X^3
\end{pmatrix}:=
\begin{pmatrix}a^1_{\ 1}X^1+a^1_{\ 2}X^2+a^1_{\ 3}X^3
\\a^2_{\ 1}X^1+a^2_{\ 2}X^2+a^2_{\ 3}X^3
\\a^3_{\ 1}X^1+a^3_{\ 2}X^2+a^3_{\ 3}X^3\end{pmatrix}\]
このように計算することにしましょう。この行列とベクトルの計算方法は
\[\begin{pmatrix}
Y^1\\Y^2\\Y^3\end{pmatrix}=(a^i_{\ j})\begin{pmatrix}X^1\\X^2\\X^3\end{pmatrix}\]
行列を用いることで、行列をすっきり書くことができます。
さらに、基底ベクトルに関しても行列の計算が使えるように拡張すれば、
\[\begin{pmatrix}
e_1\\e_2\\e_3\end{pmatrix}=(a^j_{\ i})\begin{pmatrix}e'_1\\e'_2\\e'_3\end{pmatrix}\]
行列を用いて、ベクトル\(X\)の向きと大きさを保ったまま、基底ベクトルと、成分を変えることができます。これをベクトルの座標変換と呼びます。ではベクトルの座標変換を示していきます。ベクトル\(X\)が2つの基底ベクトルの組\(\{e_1,\cdots,e_m\},\ \{e'_1,\cdots,e'_m\}\)を用いて、
\[X=\sum_{i=1}^mX^ie_i=\sum_{j=1}^mX'^je'_j\]
と表せるとしましょう。ベクトルの成分には、
\[\begin{pmatrix}
X'^1\\\vdots\\X'^3\end{pmatrix}
=\begin{pmatrix}
a^1_{\ 1}&\cdots&a^1_{\ 3}\\
\vdots&\ddots&\vdots\\
a^m_{\ 1}&\cdots&a^m_{\ m}\end{pmatrix}\begin{pmatrix}X^1\\\vdots\\X^3\end{pmatrix}\]
という変換が成り立っているとします。任意の\(j\)について、
\[X'^j=a^1_{\ 1}X^1+\cdots+a^1_{\ m}X^m\]
なので、座標変換はより短く、
\[X'^j=\sum_{l=1}^ma^{j}_{\ l}X^l\]
と表せます。ベクトル\(X\)を\(\{e'_1,\cdots,e'_m\}\)を基底として、表して成分の座標変換を代入してみます。
\[\sum_{j=1}^mX'^je'_j=\sum_{j=1}^m\left(\sum_{l=1}^ma^{j}_{\ l}X^l\right)e'_j\]
\(l\)の添え字に関して、積の総和その2\(\sum_ja_j(\sum_lb_l)=\sum_j\sum_la_jb_l\)を使って総和記号を前に持ってきます。
\[=\sum_{l=1}^m\sum_{j=1}^ma^{j}_{\ l}X^le'_j=\sum_{l=1}^m\sum_{j=1}^mX^la^{j}_{\ l}e'_j\]
次は、\(j\)の添え字について、積の総和その2\(\sum_l\sum_ja_lb_j=\sum_la_l(\sum_jb_j)\)を使います。
\[\sum_{j=1}^mX'^je'_j=\sum_{l=1}^mX^l\left(\sum_{j=1}^ma^j_{\ l}e'_j\right)\]
左辺の添え字\(l\)は総和記号もついているためダミーの添え字で\(i\)に変えます。基底\(\{e_1,\cdots,e_m\}\)を用いたベクトル\(X\)と比較すると、
\[\sum_{i=1}^mX^i\left(\sum_{j=1}^ma^j_{\ i}e'_j\right)=\sum_{i=1}^mX^ie_i\]
両辺の比較から、
\[e_i=\sum_{j=1}^ma^j_{\ i}e'_j\]
成分の座標変換と向きが逆です。そのうえ、行列の\(i\)と\(j\)が入れ替わっています。
\[\begin{array}{ccc}X^i & \xrightarrow{a^i_{\ j}} & X'^j\\
e_i & \xleftarrow{a^j_{\ i}} & e'_j
\end{array}\]
行列\(a^j_{\ i}\)は行列\(a^i_{\ j}\)の転置などとも言います。表記法は色々あります。
\[^t(a^i_{\ j})=(a^i_{\ j})^T=(a^j_{\ i})\]
ではベクトルの座標変換の例を見てみましょう。
例1 成分の定数倍
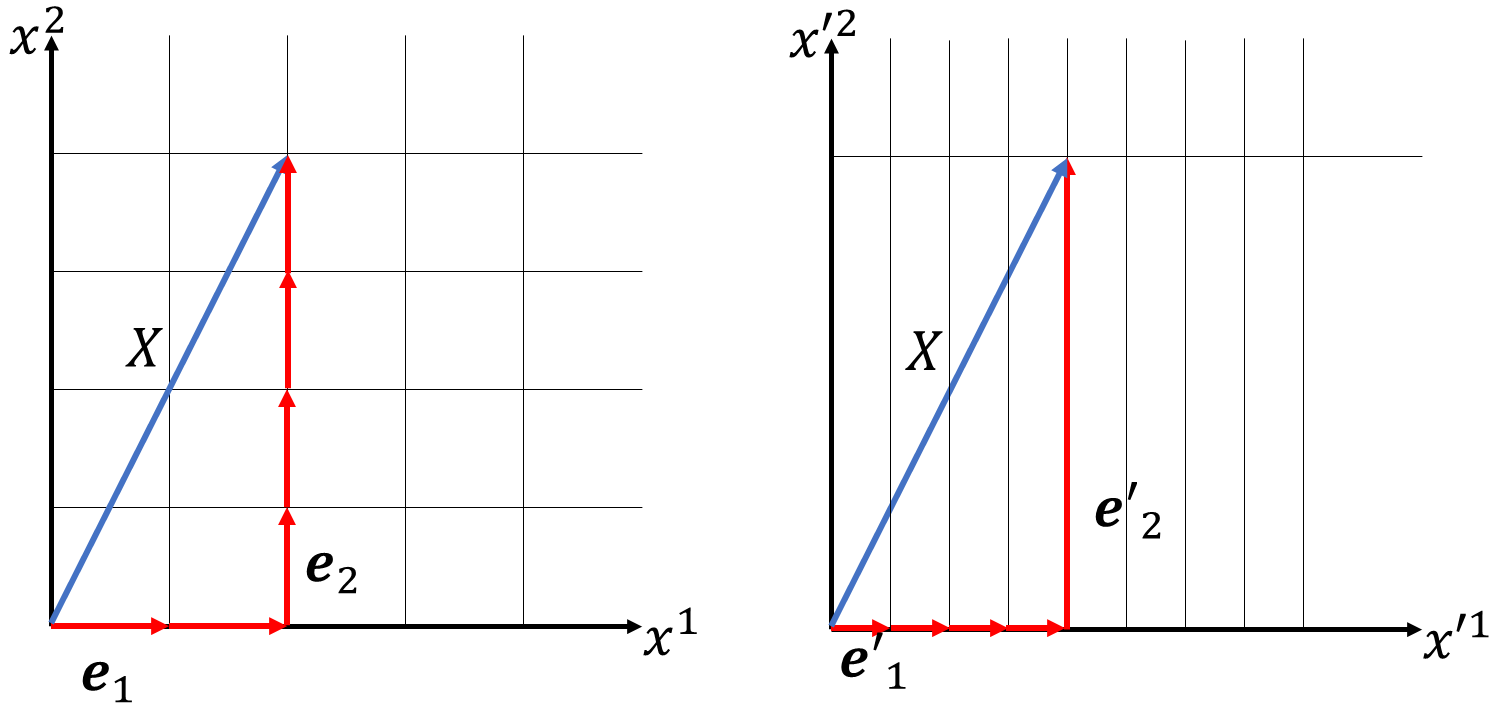
成分を\(x^1\)方向に2倍、成分を\(x^2\)方向に1/4倍します。
\[\begin{pmatrix}X'^1\\
X'^2\end{pmatrix}
=\begin{pmatrix}2&0\\
0&1/4\end{pmatrix}
\begin{pmatrix}X^1\\
X^2\end{pmatrix}
\]
図より基底ベクトルは、
\[\begin{pmatrix}e_1\\
e_2\end{pmatrix}
=\begin{pmatrix}2&0\\
0&1/4\end{pmatrix}
\begin{pmatrix}e'_1\\
e'_2\end{pmatrix}
\]
と変換されることが分かります。0と0の交換なので、転置行列であることが分かりずらいですね。
例2 基底ベクトルの回転
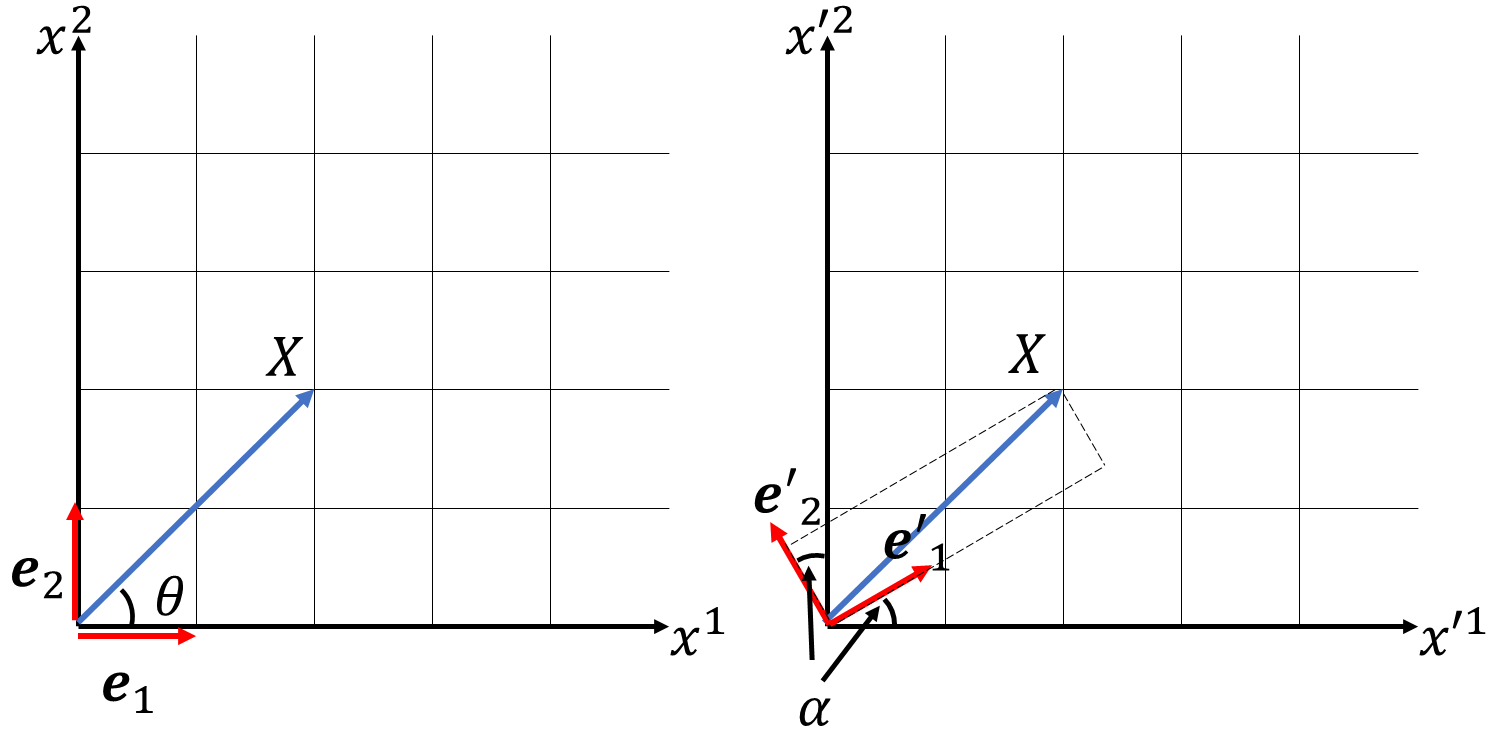
ベクトル\(X\)を、標準基底を用いて、成分が、
\[\begin{pmatrix}X^1\\X^2\end{pmatrix}=\begin{pmatrix}|X|\cos\theta\\|X|\sin\theta\end{pmatrix}\]
と与えられたとすれば、
標準基底を反時計回りに角度\(\alpha\)回転させたベクトルを基底としたときの成分は、
\[\begin{pmatrix}X'^1\\X'^2\end{pmatrix}=\begin{pmatrix}|X|\cos(\theta-\alpha)\\|X|\sin(\theta-\alpha)\end{pmatrix}\]
加法定理を用いて、
\[=\begin{pmatrix}|X|\cos\theta\cos\alpha+|X|\sin\theta\sin\alpha\\
|X|\sin\theta\cos\alpha-|X|\cos\theta\sin\alpha\end{pmatrix}\]
\[=\begin{pmatrix}X^1\cos\alpha+X^2\sin\alpha\\
-X^1\sin\alpha+X^2\cos\alpha\end{pmatrix}\]
\[\begin{pmatrix}X'^1\\X'^2\end{pmatrix}=\begin{pmatrix}\cos\alpha&\sin\alpha\\
-\sin\alpha&\cos\alpha\end{pmatrix}\begin{pmatrix}X^1\\X^2\end{pmatrix}\]
なんと回転も行列によって表すこともできます。基底ベクトル\(\boldsymbol{e}'_1,\boldsymbol{e}'_2\)は、図より
\[\boldsymbol{e}'_1=(\cos\alpha,\ \sin\alpha),\ \boldsymbol{e}'_2=(-\sin\alpha,\ \cos\alpha)\]
と分かります。この基底ベクトルの組に転置行列をかけると、
\[\begin{pmatrix}\cos\alpha&-\sin\alpha\\
\sin\alpha&\cos\alpha\end{pmatrix}\begin{pmatrix}(\cos\alpha,\ \sin\alpha)\\
(-\sin\alpha,\ \cos\alpha)\end{pmatrix}\]
\[=\begin{pmatrix}(\cos^2\alpha,\ \cos\alpha\sin\alpha)+(\sin^2\alpha,-\ \cos\alpha\sin\alpha)\\
(\cos\alpha\sin\alpha,\ \sin^2\alpha)+(-\cos\alpha\sin\alpha,\ \cos^2\alpha)
\end{pmatrix}\]
\[=\begin{pmatrix}(1,0)\\
(0,1)\end{pmatrix}=\begin{pmatrix}\boldsymbol{e}_1\\
\boldsymbol{e}_2\end{pmatrix}\]
今回のまとめです。
\[\begin{array}{ccc}X^i & \xrightarrow{a^i_{\ j}} & X'^j\\
e_i & \xleftarrow{a^j_{\ i}} & e'_j
\end{array}\]
成分の座標変換を表す行列の転置行列を変換後の基底ベクトルにかけると、元の基底ベクトルが得られます。



