楽しい科学(理論)チャンネル
多様体間の写像
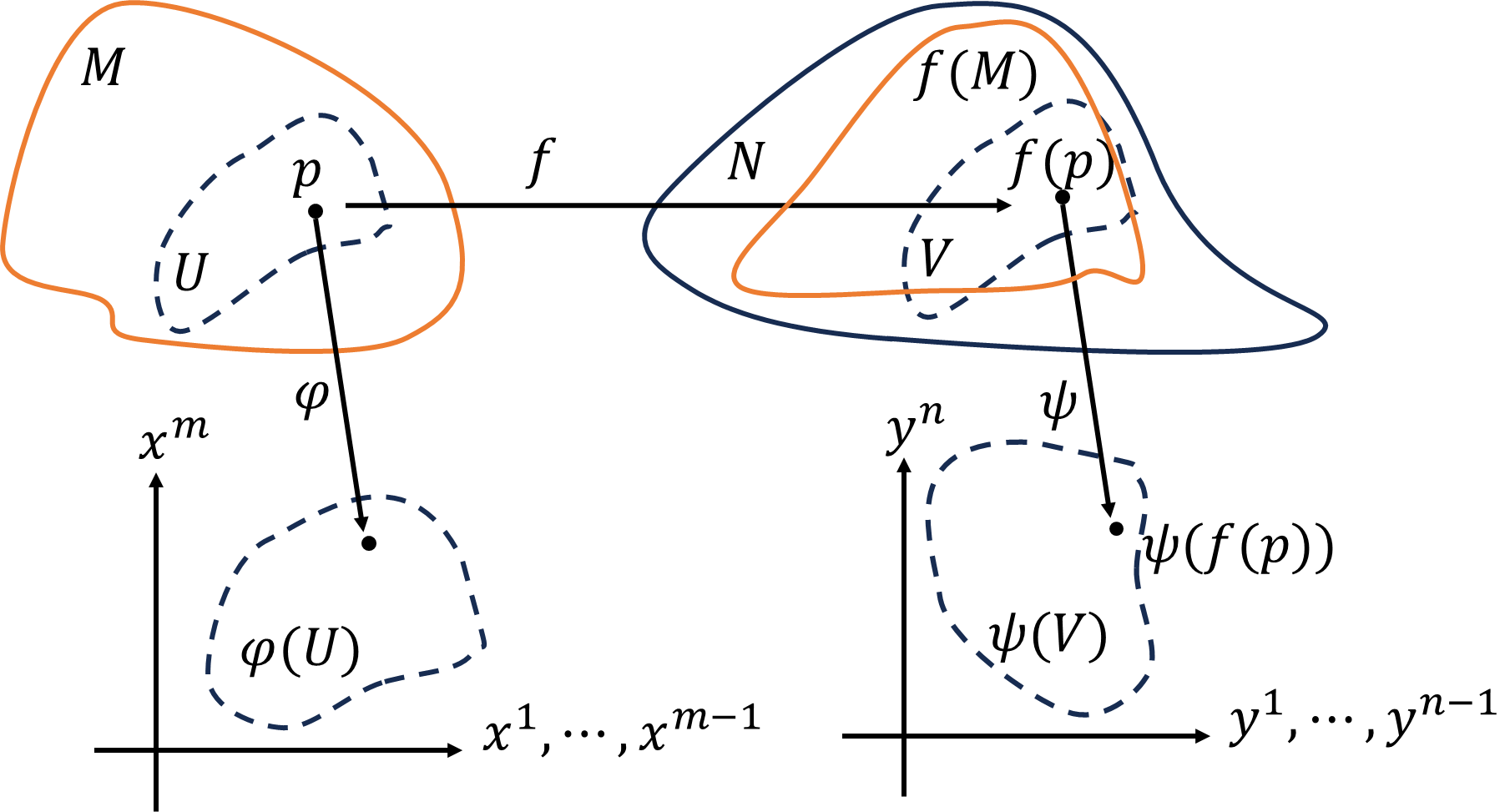
\(m\)次元多様体\(M\)、\(n\)次元多様体\(N\)について、写像\(f:M\to N\)を考えます。\(M\)上の任意の点\(p\)について、\(p\)を含む任意の局所座標を\(\varphi=(x^1,\cdots,x^m)\)、\(f(p)\)を含む任意の局所座標を\(\psi=(y^1,\cdots,y^n)\)とします。状況設定がやや複雑ですが、これ以上複雑な設定は出てきません。\(M\)上の点\(p\)は写像\(f\)によって、\(f(p)\)に写されます。更に、\(f(p)\)は同相写像\(\psi\)によって、\(n\)次元ユークリッド空間上の点\(\psi(f(p))\)に写されます。\(\psi(f(p))\)を\(x^1,\cdots,x^m\)を用いて表すと、
\[\psi(f(p))=\psi\circ f(p)=\psi\circ f\circ\varphi^{-1}(x^1,\cdots,x^m)\]
となります。つまり\(x^1,\cdots,x^m\)を決めると、各\(y^j\)が1つ定まります。
\[y^j=y^j(x^1,\cdots,x^m)\]
\(y^j\)をどのような順番でも\(x^1,\cdots,x^m\)で、任意の開数回微分できるとき、(\(C^\infty\)級であるとき)\(f:M\to N\)をなめらかな写像といいます。\(f\)は全単射でないので、\(q\in N\)については、必ずしも\(f^{-1}(q)\)が存在するわけではありませんので注意しましょう。逆写像\(f^{-1}\)を定義していないので、
\[\varphi(p)=\varphi(f^{-1}(f(p)))=\varphi\circ f^{-1}\circ\psi^{-1}(y^1,\cdots,y^n)\]
として、\(y^1,\cdots,y^n\)を決定しても各\(x^i=(y^1,\cdots,y^n)\)が決まるとは限りません。この状況設定で、\(M\)を定義域とする対象\(A_M\)を写像\(f\)によって自然に\(N\)を定義域とする対象\(A_N\)に変えることができれば押し出しと呼び、
\[f_*A_M:=A_N\]
\(N\)上の対象\(A_N\)を写像\(f\)によって自然に\(A_M\)に写せる場合引き戻しと呼び
\[f^*A_N:=A_M\]
と書くことにします。自然にとはちょっとあやふやな表現だと私は思うので、以下の例を見た方が理解が早いと思います。
関数の引き戻し
\(M\)上の点\(p\)をスカラーに写す関数\(g:M\to\mathbb{R}\)を写像\(f:M\to N\)によって\(N\)上の点\(q=f(p)\)によってスカラーが決まる関数を作ろうとします。
\[g(p)=g(f^{-1}(f(p)))=g\circ f^{-1}(q)\]
逆写像\(f^{-1}\)が出てきてしまいました。そもそも\(N\)上の点すべてを定義域にできません。\(M\)上の関数\(g\)を\(N\)に押し出すことはできません。\(N\)上の関数\(h:N\to\mathbb{R}\)を\(M\)上の点\(p\)によってスカラーが決まるように関数を作ってみます。
\[h(q)=h(f(p))=h\circ f(p)\]
\(f(M)\subset N\)なので、に\(h\)の地域が狭くなってしまいましたが、\(N\)の関数\(h\)を、\(M\)に引き戻すことができます。引き戻しは記号で\(f^*\)と表し引き戻したい対象の右側から作用させます。
\[f^*h:=h\circ f\]
図にまとめるとこんな感じです。
\[\begin{array}{ccccc}
M&\xrightarrow{f}&N&\xrightarrow{h}&\mathbb{R}\\
\cssId{rotin90}{\ni}& &\cssId{rotin90}{\ni}& &\cssId{rotin90}{\ni}\\
p&\longmapsto&f(p)&\longmapsto&h(f(p))&=:f^*h\end{array}\]
これが自然な流れです。\(N\)上の関数\(h:N\to\mathbb{R}\)を写像\(f:M\to N\)によって\(M\)上の関数\(f^*h:M\to\mathbb{R}\)に引き戻しをしています。
\[\begin{array}{ccccc}
\mathbb{R}&\xleftarrow{g}&M&\xrightarrow{f}&N\\
\cssId{rotin90}{\ni}& &\cssId{rotin90}{\ni}& &\cssId{rotin90}{\ni}\\
g(\cancel{f^{-1}(q)})&\cssId{rotin180}{\longmapsto}&\cancel{f^{-1}(q)}&\longmapsto&q\end{array}\]
\(M\)上の関数を\(N\)に押し出せません。なぜなら逆写像\(f^{-1}:N\to M\)が定義されていないからです。
接ベクトルの押し出し
接ベクトルについてちょっと復習します。\(M\)上の\(t\in\mathbb{R}\)をパラメータとする曲線\(C(t)\)について、点\(p\)接ベクトル\(X_p\)は、\(C(t)\)上のスカラー値関数\(g:M\to\mathbb{R}\)に作用する点\(p\)における微分作用素として定義されます。
\[X_p(\Box):=\left.\frac{d\ \Box\circ C(t)}{dt}\right|_{t=t_p}\in T_pM\]
\(t_p\)は\(p=C(t_p)\)となる\(t\)です。簡単に\(t_p=0\)としている本がほとんどです。多様体上の曲線、多様体上の点のみから決定して座標に依りません。\(\Box\)には関数\(g:C(t)\to\mathbb{R}\)を代入できます。写像\(f:M\to N\)によって、\(M\)上の点\(p\)は\(f(p)\)に写されます。曲線\(C(t)\in M\)は\(f(C(t))\in N\)に写されます。曲線\(f\circ C\)上の点\(f(p)\)の接ベクトルは、\(X_p,f\)から自然に
\[f_*X_p:=X_{f(p)}(\Box\circ f)=\left.\frac{d\Box\circ f\circ C(t)}{dt}\right|_{t=t_{p}}\in T_{f(p)}N\]
と決めることができます。接ベクトルの押し出しは、作用する関数の引き戻して、点\(p\)の押し出すことと同じです。接ベクトルから、接ベクトルの押し出しを得る写像を写像の微分\((df)_p:T_pM\to T_{f(p)}N\)と呼びます。
\[\begin{array}{ccccc}
T_pM&\stackrel{(df)_p}{\longrightarrow}&T_{f(p)}N\\
\cssId{rotin90}{\ni}&&\cssId{rotin90}{\ni}\\
\left.\frac{d}{dt}\right|_{t=t_p}\Box\circ C(t)&\longmapsto&\left.\frac{d}{dt}\right|_{t=t_p}\Box\circ f\circ C(t)\\
\cssId{rotin90}{=}&&\cssId{rotin90}{=:}\\
X_p&\longmapsto&f_*X_p
\end{array}\]
\(N\)上の曲線\(D\)や\(N\)上の点\(q\)を写像\(f:M\to N\)によって\(M\)上に持ってくることはできません。なぜなら逆写像\(f^{-1}:N\to M\)が定義されていないからです。
\[\begin{array}{ccccc}
T_{\cancel{f^{-1}(q)}}M&\stackrel{(df)_p}{\longrightarrow}&T_{q}N\\
\cssId{rotin90}{\ni}&&\cssId{rotin90}{\ni}\\
\left.\frac{d}{du}\right|_{u=u_q}\Box\circ \cancel{f^{-1}\circ D(u)}&\longmapsto&\left.\frac{d}{du}\right|_{u=u_q}\Box\circ D(u)\\
\cssId{rotin90}{}&&\cssId{rotin90}{=}\\
&&Y_q
\end{array}\]
\(T_qN\)の接ベクトルを\(T_pM\)に引き戻すことはできません。ここからは覚えなくてもいいですが、局所座標\(p\in U,\varphi(U)=(x^1,\cdots,x^m),\ q\in V,\psi(V)=(y^1,\cdots,y^n)\)を決めれば、写像の微分\((df)_p\)は行列を用いて表すことができます。点\(\psi(q)\)は、写像\(\varphi^{-1}\circ f\circ\psi:\varphi(p)\mapsto\psi(q)\)によって\(\varphi\)の変数を用いて表せるはずなので、
\[\begin{pmatrix}y^1\\\vdots\\y^n\end{pmatrix}=\begin{pmatrix}y^1(x^1,\cdots,x^m)\\\vdots\\y^n(x^1,\cdots,x^m)\end{pmatrix}\]
と表すことにします。
\[X_p(\Box)=\sum_{i=1}^mX_p^i\left(\frac{\partial}{\partial x^i}\right)_p=\sum_{i=1}^mX_p^i\frac{\partial \Box}{\partial x^i}(p)\]
と表すれば、チェーンルールから
\[f_*X_p(\Box)=\sum_{j=1}^mX_p^i\frac{\partial \Box\circ f}{\partial x^i}(f(p))\]
\[=\sum_{i=1}^m\sum_{j=1}^nX_{p}^i\frac{\partial y^j}{\partial x^i} (\varphi(p))\frac{\partial\Box\circ f}{\partial y^j}(f(p))\]
\[=\sum_{i=1}^m\sum_{j=1}^nX_{p}^i\frac{\partial y^j}{\partial x^i} (\varphi(p))\left(\frac{\partial}{\partial y^j}\right)_{f(p)}\]
接ベクトルの基底\(\{(\frac{\partial}{\partial x^1})_p,\cdots,(\frac{\partial}{\partial x^m})_p\}\)、\(\{(\frac{\partial}{\partial y^1})_{f(p)},\cdots,(\frac{\partial}{\partial y^n})_{f(p)}\}\)の係数部分を並べて列ベクトルを作ると、
\[X_p=\begin{pmatrix}X_{p}^1\\
\vdots\\
X_{p}^m\end{pmatrix}\]
\[f_*X_p=\begin{pmatrix}X_{p}^1\frac{\partial y^1}{\partial x^1} (\varphi(p))+&\cdots&+X_{p}^m\frac{\partial y^1}{\partial x^m} (\varphi(p))\\
\vdots&\ddots&\vdots\\
X_{p}^1\frac{\partial y^n}{\partial x^1} (\varphi(p))+&\cdots&+X_{p}^m\frac{\partial y^n}{\partial x^m} (\varphi(p))\end{pmatrix}\]
となります。ここで、写像の微分を
\[(df)_p:=\begin{pmatrix}\frac{\partial y^1}{\partial x^1} (\varphi(p))&\cdots&\frac{\partial y^1}{\partial x^m} (\varphi(p))\\
\vdots&\ddots&\vdots\\
\frac{\partial y^n}{\partial x^1} (\varphi(p))&\cdots&\frac{\partial y^n}{\partial x^m} (\varphi(p))\end{pmatrix}\]
このように行列で定義することで、
\[(df)_pX_p=f_*X_p\]
接ベクトルの押し出し\(f_*X_p\)は接ベクトル\(X_p\)に写像の微分\((df)_p\)を作用させたものとなります。\(x^i\)を\(y^j\)を変数として表すことはできません。なぜなら逆写像\(\psi^{-1}\circ f^{-1}\circ\varphi\)が定義できません。そのため\((df^{-1})_p\)も定義できません。
ベクトル場の押し出し
ベクトル場は押し出しです。ベクトル場\(X\in\mathfrak{X}\)はチャート\(\varphi(U)=(x^1,\cdots,x^m)\)上で
\[X|_U(\Box)=\sum_{i=1}^mX^i\frac{\partial \Box}{\partial x^i}\]
と与えられます。\(X|_U\)は\(X\)を\(U\)上に制限するという意味です。省略する場合もあります。\(X^i\)はチャート上の関数で\(\Box\)には多様体上の関数が入ります。任意の点\(p\in U\)においては、接ベクトルと同様のふるまいをっするため、ベクトル場も同様に押し出しとなります。
\[f_*X(\Box)=X(\Box\circ f)\]
余接ベクトルの引き戻し
余接ベクトル\(\alpha_p\in T_p^*M\)は引き戻しです。余接ベクトルは、接ベクトルを実数に写す線形写像でした。局所座標では具体的に
\[\alpha_p:X_p\longmapsto\sum_{i=1}^m\alpha_{p,i}X_{p}^i\in\mathbb{R}\]
接ベクトルには押し出ししかなく、\(f_*X_p\in T_{f(p)}N\)を実数に写す線形写像は、
\[\alpha_{f(p)}(f_*X_p)=\sum_{\mu=1}^n\alpha_{f(p),\mu}(dy^{\mu})_{f(p)}\left(f_*X_p\right)\]
\[=\sum_{\mu=1}^n\alpha_{f(p),\mu}(dy^{\mu})_{f(p)}\left(\sum_{i=1}^m\sum_{j=1}^nX_p^i\frac{\partial y^j}{\partial x^i}(\varphi(p))\left(\frac{\partial }{\partial y^j}\right)_{f(p)}\right)\]
\[=\sum_{\mu=1}^n\alpha_{f(p),\mu}\sum_{i=1}^m\sum_{j=1}^nX_p^i\frac{\partial y^j}{\partial x^i}(\varphi(p))(dy^{\mu})_{f(p)}\left(\left(\frac{\partial }{\partial y^j}\right)_{f(p)}\right)\]
\[=\sum_{i=1}^m\sum_{j=1}^n\sum_{\mu=1}^n\alpha_{f(p),\mu}X_p^i\frac{\partial y^j}{\partial x^i}(\varphi(p))\delta^\mu_j\]
\[=\sum_{\mu=1}^n\sum_{i=1}^m\alpha_{f(p),\mu}\frac{\partial y^\mu}{\partial x^i}(\varphi(p))(dx^i)_p(X_p)\]
少し見やすくするために定数\(\alpha_{p,i}\)を
\[\alpha_{p,i}=\sum_{\mu=1}^n\alpha_{f(p),\mu}\frac{\partial y^\mu}{\partial x^i}(\varphi(p))\]
とします。\(X_p^i=(dx^{i})_p(X_p)\)より、
\[\alpha_{f(p)}(f_*X_p)=\sum_{i=1}^m\alpha_{p,i}(dx^i)_p(X_p)\]
これは、\(M\)上の点\(p\)における余接ベクトルです。これを余接ベクトルの引き戻しと定義します。
\[\alpha_{f(p)}(f_*X_p)=\alpha_p(X_p)\]
余接ベクトルの引き戻しも行列を用いて表すと、
\[\begin{pmatrix}\alpha_{p,1}\\
\vdots\\
\alpha_{p,m}
\end{pmatrix}
=\begin{pmatrix}\frac{\partial y^1}{\partial x^1}(\varphi(p))\alpha_{f(p),1}+&\cdots&+\frac{\partial y^n}{\partial x^1}(\varphi(p))\alpha_{f(p),n}\\
\vdots&\ddots&\vdots\\
\frac{\partial y^1}{\partial x^m}(\varphi(p))\alpha_{f(p),1}+&\cdots&+\frac{\partial y^n}{\partial x^m}(\varphi(p))\alpha_{f(p),n}\end{pmatrix}\]
\[\begin{pmatrix}\alpha_{p,1}\\
\vdots\\
\alpha_{p,m}
\end{pmatrix}
=\begin{pmatrix}\frac{\partial y^1}{\partial x^1}(\varphi(p))&\cdots&\frac{\partial y^n}{\partial x^1}(\varphi(p))\\
\vdots&\ddots&\vdots\\
\frac{\partial y^1}{\partial x^m}(\varphi(p))&\cdots&\frac{\partial y^n}{\partial x^m}(\varphi(p))\end{pmatrix}\begin{pmatrix}\alpha_{f(p),1}\\
\vdots\\
\alpha_{f(p),n}
\end{pmatrix}\]
この行列を\((df)_p^*\)と表すことにすれば、\((df)_p\)の転置の転置行列であり逆方向に変換していることが分かります。
\[\begin{array}{ccccc}
T_{p}M&\stackrel{(df)_p}{\longrightarrow}&T_{f(p)}N\\
T^*_{p}M&\stackrel{(df)^*_p}{{\longleftarrow}}&T^*_{f(p)}N\\
\cssId{rotin90}{\ni}&&\cssId{rotin90}{\ni}\\
\alpha_p(X_p)&\cssId{rotin180}{\longmapsto}&\alpha_{f(p)}(f_*X_p)&=:f^*\alpha_{f(p)}(X_p)\\
\end{array}\]
接ベクトルの押し出しを表す行列に対して、余接ベクトルの成分は逆向きの転置行列により引き戻されます。つまり双対です。余接ベクトルの基底の引き戻しは
\[f^*(dy^\mu)_{f(p)}=\sum_{i=1}^m\frac{\partial y^{\mu}}{\partial x^i}\varphi(p)(dx^i)_p\]
となります。余接ベクトルの押し出しは、\(x^i\)を\(y^j\)を変数とした関数として表せるとは限らないという接ベクトルの時と同様の理由により定義できません。
微分形式の引き戻し
微分形式には引き戻ししかありません。余接ベクトルの引き戻しから1次微分形式の引き戻しも
\[f^*\alpha=f^*\left(\sum_{\nu=1}^n\alpha_\nu dy^\nu\right)=\sum_{\nu=1}^n\sum_{\mu=1}^m\alpha_\nu\frac{\partial y^\nu}{\partial x^\mu}dx^\mu\]
となります。
1次微分形式の引き戻しが決まれば、\(k\)次微分形式は1次微分形式を用いて表せるため自然に引き戻しが決定して、\(k\)次微分形式の引き戻しは、
\[f^*\omega(\Box_1,\cdots,\Box_k)=\omega(f_*\Box_1,\cdots,f_*\Box_k)\]
このように定義されます。以下では局所座標で引き戻しが具体的にどのように表せるか見ていきます。多様体\(N\)上の\(k(\lt m,n)\)次微分形式をある局所座標で、
\[\omega=\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\]
と表せたとします。\(\lambda\)に関する総和記号は省略しています。
\[\omega(f^*X_1,\cdots,f^*X_k)=\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\delta^{\lambda_1\cdots\lambda_k}_{\nu_1\dots\nu_k}\frac{\partial y^{\nu_1}}{\partial x^{\lambda_1}}X_1^{\lambda_1}\cdots\frac{\partial y^{\nu_1}}{\partial x^{\lambda_k}}X_k^{\lambda_k}\]
\[=\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\delta^{\lambda_1\cdots\lambda_k}_{\nu_1\dots\nu_k}\frac{\partial y^{\nu_1}}{\partial x^{\lambda_1}}\cdots\frac{\partial y^{\nu_1}}{\partial x^{\lambda_k}}X_1^{\lambda_1}\cdots X_k^{\lambda_k}\]
\[=\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\frac{\partial(y^{\nu_1}\cdots y^{\nu_k})}{\partial (x^{\lambda_1}\cdots x^{\lambda_k})}X_1^{\lambda_1}\cdots X_k^{\lambda_k}\]
ヤコビアンの中の\(\lambda\)の添え字が小さい順になるように総和を取り直します。やり方は\(k\)次微分形式のチャート間の座標変換と一緒です。
\[=\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\frac{\partial(y^{\nu_1}\cdots y^{\nu_k})}{\partial (x^{\mu_1}\cdots x^{\mu_k})}\delta_{\lambda_1\cdots\lambda_k}^{\mu_1\dots\mu_k}X_1^{\lambda_1}\cdots X_k^{\lambda_k}\]
\[=\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\frac{\partial(y^{\nu_1}\cdots y^{\nu_k})}{\partial (x^{\mu_1}\cdots x^{\mu_k})}\delta_{\lambda_1\cdots\lambda_k}^{\mu_1\dots\mu_k}dx^{\lambda_1}(X_1)\cdots dx^{\lambda_k}(X_k)\]
\[=\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt \nu_k}\omega_{\nu_1\cdots\nu_k}\frac{\partial(y^{\nu_1}\cdots y^{\nu_k})}{\partial (x^{\mu_1}\cdots x^{\mu_k})}dx^{\mu_1}\wedge\cdots \wedge dx^{\mu_k}(X_1,\cdots,X_k)\]
\(M\)上の微分形式が得られましたね。
押し出し引き戻しの例
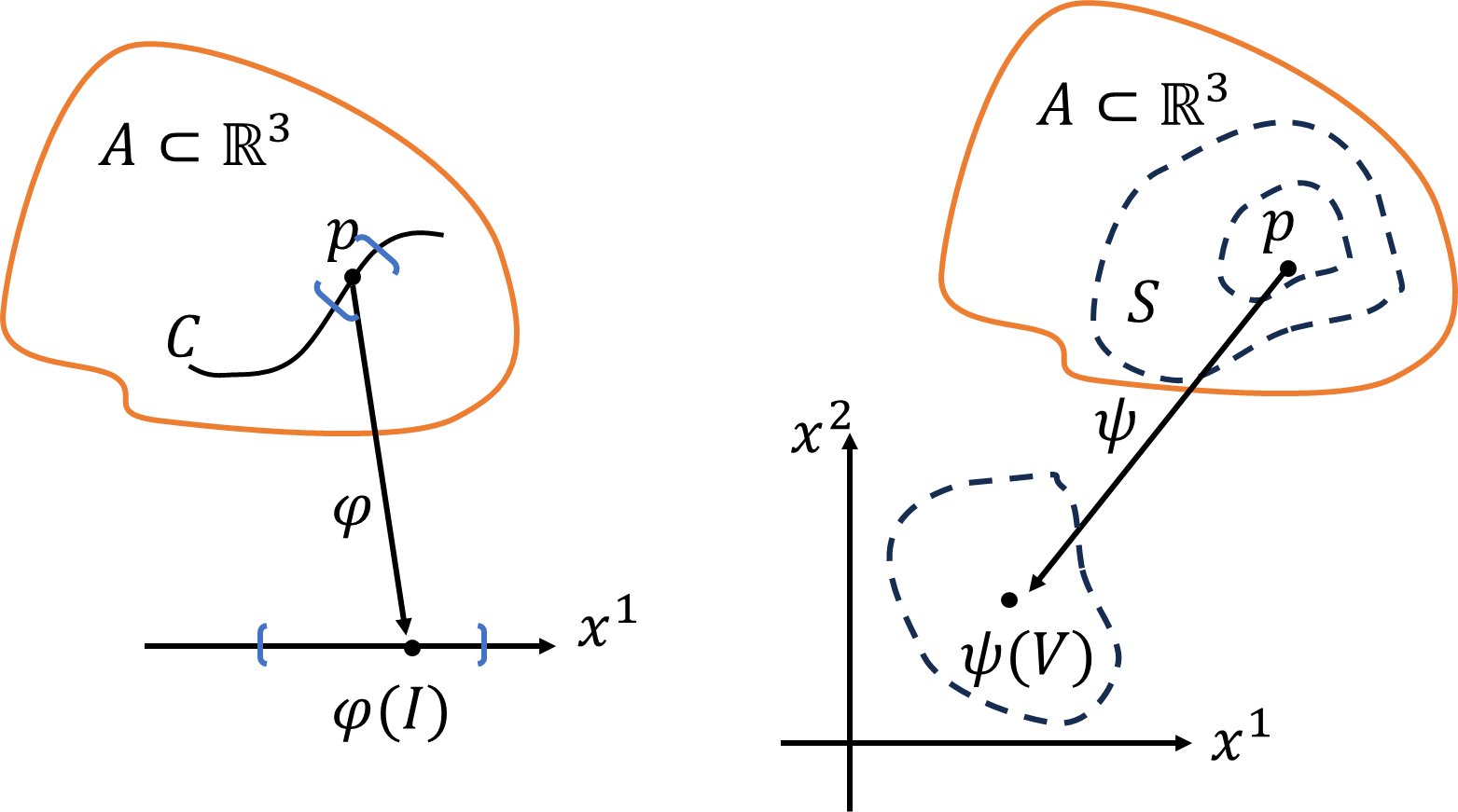
温度\(T\)は3次元空間上の関数です。3次元空間から、3次元空間上の閉集合\(A\)、曲線\(C\)曲面\(S\)があるとします。温度\(T\)は\(\mathbb{R}^3\)上のすべての点\(p\)にスカラー\(T(p)\)が割り当てられています。つまり、どの図形上の点にも温度が割り当てられているはずです。引き戻しとは\(C\)や\(A\)、\(S\)上の関数として扱うことができます。それが引き戻しです。写像
\[\iota:C\to\mathbb{R}^3,\ \eta:A\to\mathbb{R}^3,\ \tau:S\to\mathbb{R}^3\]
によって、
\[\iota^*T=T\circ\iota:C\to\mathbb{R}\]
\[\eta^*T=T\circ\eta:A\to\mathbb{R}\]
\[\tau^*T=T\circ\tau:S\to\mathbb{R}\]
別の図形上の関数とすることができます。曲線\(C\)にパラメータ\(t\)を付けます。その同相写像を\(\varphi:t\mapsto \varphi(t)\in C\)とします。微分演算子
\[\varDelta\vec{t}=\varDelta t\frac{d}{dt}\quad\varDelta t\in\mathbb{R}\]
は\(C\)上のベクトル場です。\(C\)上の関数\(h(t)\)に作用してその微分を得ることもできます。
\[\varDelta\vec{t}(h(t))=\varDelta t\frac{dh(t)}{dt}\]
写像\(\iota:C\to\mathbb{R}^3\)により3次元空間に押し出すことができます。ベクトル場の押し出しは作用する関数の引き戻しなので、
\[\iota_*\varDelta\vec{t}(h)=\varDelta t\frac{dh\circ\iota(x,y,z)}{dt}\]
\[\iota_*\varDelta\vec{t}(h)=\frac{dx}{dt}\varDelta t\frac{\partial h\circ\iota}{\partial x}+\frac{dy}{dt}\varDelta t\frac{\partial h\circ\iota}{\partial y}+\frac{dz}{dt}\varDelta t\frac{\partial h\circ\iota}{\partial z}\]
関数\(h\)はなんでもよかったので、いったん避けます。3次元空間の直交座標の\(t\)微分を速度\(v\)の記号を使います。\(v\)は\(h\circ\iota:\mathbb{R}^3\to\mathbb{R}\)の偏微分なので、\(v(x,y,z)\)などと書くべきですが省略します。
\[\iota_*\varDelta\vec{t}=v_x\varDelta t\frac{\partial }{\partial x}+v_y\varDelta t\frac{\partial}{\partial y}+v_z\varDelta t\frac{\partial}{\partial z}\]
パラメータ\(t\)を時間として曲線\(C\)上を動く物体にはたらく力を1次微分形式\(F:T_pM\to\mathbb{R}\)とします。(もちろんベクトル場ともできます。)
\[\vec{F}=F_xdx+F_ydy+F_zdz\]
経路\(C\)で動く物体に働く力\(\vec{F}\)がした仕事\(W\)は、
\[W=\int_C\vec{F}\cdot d\vec{x}\]
などと内積かつ積分で与えられますが、通常は複雑でできない為、うまいパラメータを見つけて、
\[W=\int_{t_i}^{t_f}(F_xv_x+F_yv_y+F_zv_z)dt\]
のように関数\(\sum F_iv_i:t\mapsto\mathbb{R}\)の積分に落とし込むなどの工夫が必要です。まさしくこれ微分形式の引き戻しによるものです。
\[\vec{F}(\iota_*\varDelta\vec{t\ })=(F_xv_x+F_yv_y+F_zv_z)\varDelta t\]
通常1次微分形式\(F\)には、3次元空間上の接ベクトルを代入するわけですが、曲線\(C\)の接ベクトルの押し出しを代入して、その総和を取ると\(t\)を変数とする関数の積分のリーマン和として扱えます。

