楽しい科学（理論）チャンネル

　\(M\)次元多様体上の\(k\)次微分形式\(\omega\)全体の集合を\(\Omega^k(M)\)とします。微分形式の次数を１つ挙げる写像\(d:\Omega^k(M)\to\Omega^{k+1}(M)\)が、 を満たすとき、\(d:\Omega^{k}\to\Omega^{k+1}\)を外微分と呼ぶ。

　例として３次元空間上の微分形式 \[E=E_{xy}dx\wedge dy+E_{xz}dx\wedge dz+E_{yz}dy\wedge dz\] の外微分を求めます。線形性より外微分は各項に作用します。 \[dE=d(E_{xy}dx\wedge dy)+d(E_{xz}dx\wedge dz)+d(E_{yz}dy\wedge dz)\] 1項目だけ詳しく見てみましょう。ライプニッツ則から関数\(E_{xy}\)と2つの１次微分形式\(dx,dy\)それぞれに外微分\(d\)を作用させたものを足し合わせます。 \[d(E_{xy}dx\wedge dy)\] \[=dE_{xy}\wedge dx\wedge dy+E_{xy}d(dx)\wedge dy+(-1)^{1}E_{xy}dx\wedge d(dy)\] 第３項目は１次微分形式を飛び越して外微分しているのでマイナスが付くことに注意しましょう。ちなみに1次微分形式\(dx\)は座標変数\(x\)の外微分とみなします。なので\(d(dx)=d\circ dx=0\)となります。更に\(dE_{xy}\)は外微分なので、 \[d(E_{xy}dx\wedge dy)=\left(\frac{\partial E_{xy}}{\partial x}dx+\frac{\partial E_{xy}}{\partial y}dy+\frac{\partial E_{xy}}{\partial z}dz\right)\wedge dx\wedge dy\] \(dx\wedge dx\)などの同じ微分形式を含むwedge積は０となるので、 \[d(E_{xy}dx\wedge dy)=\frac{\partial E_{xy}}{\partial z}dz\wedge dx\wedge dy\] 他の項にも同様にすれば、 \[dE=\left(\frac{\partial E_{xy}}{\partial z}-\frac{\partial E_{xz}}{\partial y}+\frac{\partial E_{yz}}{\partial x}\right)dx\wedge dy\wedge dz\] \(E_{xz}\)は添え字に対して交代性があるので、 \[dE=\left(\frac{\partial E_{xy}}{\partial z}+\frac{\partial E_{zx}}{\partial y}+\frac{\partial E_{yz}}{\partial x}\right)dx\wedge dy\wedge dz\] としてもサイクリック\(\cdots\to x\to y\to z\to x\to\cdots\)な表記できれいだと思います。ここまで計算できれば外微分の計算方法は理解できています。

　外微分を座標を使わずに定義しましたが、これが座標に依らない定義になっているか見ていきます。多様体\(M\)上のチャート\((U_1,\varphi_1),(U_2,\varphi_2)\)が\(U_1\cap U_2\neq\varnothing\)であるとき、\(U_1\cap U_2\)上で微分形式\(\omega\)の外微分が局所座標\(\varphi_1=(x^1,\cdots,x^m),\varphi_2=(y^1,\cdots,y^m)\)に依らず等しいことを確認します。\(k\)次微分形式\(\omega\)は、\(\varphi_1\)の座標で、 \[\omega=\sum_{\mu_1\lt\cdots\lt\mu_k}\omega_{\mu_1\cdots\mu_k}dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}\] とすると、\(\varphi_2\)の座標で、 \[\omega=\sum_{\mu_1\lt\cdots\lt\mu_k}\sum_{\nu_1\lt\cdots\lt\nu_k}\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}\omega_{\mu_1\cdots\mu_k}dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] と表されますね。\(\varphi_1\)の座標では \[d\omega=\sum_{\mu_1\lt\cdots\lt\mu_k}d\omega_{\mu_1\cdots\mu_k}\wedge dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}\] \(d\)は線形性から、総和記号を通り抜けて各項の関数部分を全微分にします。 \(\varphi_2\)で表した\(\omega\)を外微分して、\(\varphi_1\)で表した\(\omega\)で表した\(d\omega\)と等しいことを確認すればよいので、 \[d\omega=\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt\nu_k}\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}d\omega_{\mu_1\cdots\mu_k}\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] \[+\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt\nu_k}\omega_{\mu_1\cdots\mu_k}d\left(\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}\right)\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] １項目は、(総和記号は省略します。) \[\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}d\omega_{\mu_1\cdots\mu_k}\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] 外微分の影響で\(k+1\)次微分形式となり\(k+1\)この接ベクトルが代入できます。 \[=\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}\frac{\partial\omega_{\mu_1\cdots\mu_k}}{\partial y^\nu}dy^\nu\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}(\Box_1,\cdots,\Box_{k+1})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\frac{\partial x^{\rho_1}}{\partial y^{\nu_1}}\cdots\frac{\partial x^{\rho_k}}{\partial y^{\nu_k}}\frac{\partial\omega_{\mu_1\cdots\mu_k}}{\partial y^\nu}\delta_{1\cdots k+1}^{\lambda\lambda_1\cdots\lambda_k}\] \[dy^\nu(\Box_\lambda)dy^{\nu_1}(\Box_{\lambda_{1}})\cdots dy^{\nu_k}(\Box_{\lambda_{k}})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\delta_{1\cdots k+1}^{\lambda\lambda_1\cdots\lambda_k}\frac{\partial\omega_{\mu_1\cdots\mu_k}}{\partial y^\nu}dy^\nu(\Box_\lambda)\frac{\partial x^{\rho_1}}{\partial y^{\nu_1}}dy^{\nu_1}(\Box_{\lambda_{1}})\cdots\frac{\partial x^{\rho_k}}{\partial y^{\nu_k}}dy^{\nu_k}(\Box_{\lambda_{k}})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\delta_{1\cdots k+1}^{\lambda\lambda_1\cdots\lambda_k}d\omega_{\mu_1\cdots\mu_k}(\Box_\lambda)dx^{\rho_1}(\Box_{\lambda_{1}})\cdots dx^{\rho_k}(\Box_{\lambda_{k}})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}d\omega_{\mu_1\cdots\mu_k}\wedge dx^{\rho_1}\wedge\cdots\wedge dx^{\rho_k}(\Box_1,\cdots,\Box_{k+1})\] \[=d\omega_{\mu_1\cdots\mu_k}\wedge dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_k}(\Box_1,\cdots,\Box_{k+1})\] １項目は\(\varphi\)で表した微分形式の全微分となっています。つまり２項目が０であることを示せばよいです。 \[\sum_{\mu_1\lt\cdots\lt \mu_k}\sum_{\nu_1\lt\cdots\lt\nu_k}\omega_{\mu_1\cdots\mu_k}d\left(\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}\right)\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] 総和記号は省略します。 \[=\omega_{\mu_1\cdots\mu_k}d\left(\frac{\partial(x^{\mu_1},\cdots,x^{\mu_k})}{\partial(y^{\nu_1},\cdots,y^{\nu_k})}\right)\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}(\Box_1\cdots\Box_{k+1})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\delta^{\lambda\lambda_1\cdots\lambda_{k}}_{1\cdots k+1}\omega_{\mu_1\cdots\mu_k}\frac{\partial }{\partial y^{\nu}}\left(\frac{\partial x^{\rho_1}}{\partial y^{\nu_1}}\cdots\frac{\partial x^{\rho_k}}{\partial y^{\nu_k}}\right)\] \[dy^\nu(\Box_{\lambda})dy^{\nu_1}(\Box_{\lambda_1})\cdots dy^{\nu_k}(\Box_{\lambda_{k+1}})\] \(\frac{\partial}{\partial y^\nu}\)のライプニッツ則から \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\delta^{\lambda\lambda_1\cdots\lambda_{k}}_{1\cdots k+1}\left(\frac{\partial^2 x^{\rho_1}}{\partial y^\nu\partial y^{\nu_1}}\cdots\frac{\partial x^{\rho_k}}{\partial y^{\nu_k}}+\cdots+\frac{\partial x^{\rho_1}}{\partial y^{\nu_1}}\cdots\frac{\partial^2 x^{\rho_k}}{\partial y^\nu\partial y^{\nu_k}}\right)\] \[\omega_{\mu_1\cdots\mu_k}dy^\nu(\Box_{\lambda})dy^{\nu_1}(\Box_{\lambda_1})\cdots dy^{\nu_k}(\Box_{\lambda_{k+1}})\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\delta^{\lambda\lambda_1\cdots\lambda_{k}}_{1\cdots k+1}\omega_{\mu_1\cdots\mu_k}\] \[\left(\frac{\partial^2 x^{\rho_1}}{\partial y^\nu\partial y^{\nu_1}}dy^\nu(\Box_\lambda)dy^{\nu_1}(\Box_{\lambda_1})dx^{\rho_2}(\Box_{\lambda_2})\cdots dx^{\rho_k}(\Box_{\lambda_{k+1}})\right.\] \[\left.+\cdots+\frac{\partial^2 x^{\rho_k}}{\partial y^\nu\partial y^{\nu_k}}dy^{\nu}(\Box_{\lambda})dx^{\rho_1}(\Box_{\lambda_1})\cdots dx^{\rho_{k-1}}(\Box_{\lambda_k})dy^{\nu_k}(\Box_{\lambda_{k+1}})\right)\] \[=\delta^{\mu_1\cdots\mu_k}_{\rho_1\cdots\rho_k}\omega_{\mu_1\cdots\mu_k}\left(\frac{\partial^2 x^{\rho_1}}{\partial y^\nu\partial y^{\nu_1}}dy^\nu\wedge dy^{\nu_1}\wedge dx^{\rho_2}\wedge\cdots \wedge dx^{\rho_k}\right.\] \[\left.+\cdots+\frac{\partial^2 x^{\rho_k}}{\partial y^\nu\partial y^{\nu_k}}dy^{\nu}\wedge dx^{\rho_1}\wedge\cdots\wedge dx^{\rho_{k-1}}\wedge dy^{\nu_k}\right)\] \[=\omega_{\mu_1\cdots\mu_k}\frac{\partial^2 x^{\mu_1}}{\partial y^\nu\partial y^{\nu_1}}dy^\nu\wedge dy^{\nu_1}\wedge dx^{\mu_2}\wedge\cdots \wedge dx^{\mu_k}\] \[+\cdots+\omega_{\mu_1\cdots\mu_k}\frac{\partial^2 x^{\mu_k}}{\partial y^\nu\partial y^{\nu_k}}dy^{\nu}\wedge dx^{\mu_1}\wedge\cdots\wedge dx^{\mu_{k-1}}\wedge dy^{\nu_k}\] 微分形式はもともと成分と基底両方が交代性を持っていますが、しかし\(dy^i\wedge dy^j\)は交代性を持ちますが、\(\frac{\partial x^\mu}{\partial y^i\partial y^j}\)は交代性を持ちません。そのため\(i\lt j\)と\(i\gt j\)の項で打ち消します。以上から微分形式の外微分は、チャートに依らずwell-definedであるといえます。

微分形式のチャート間の座標変換は、引き戻しの１種でした。ということは、引き戻してから外微分と外微分してから引き戻しが一致すれば、外微分がwell-definedといえます。

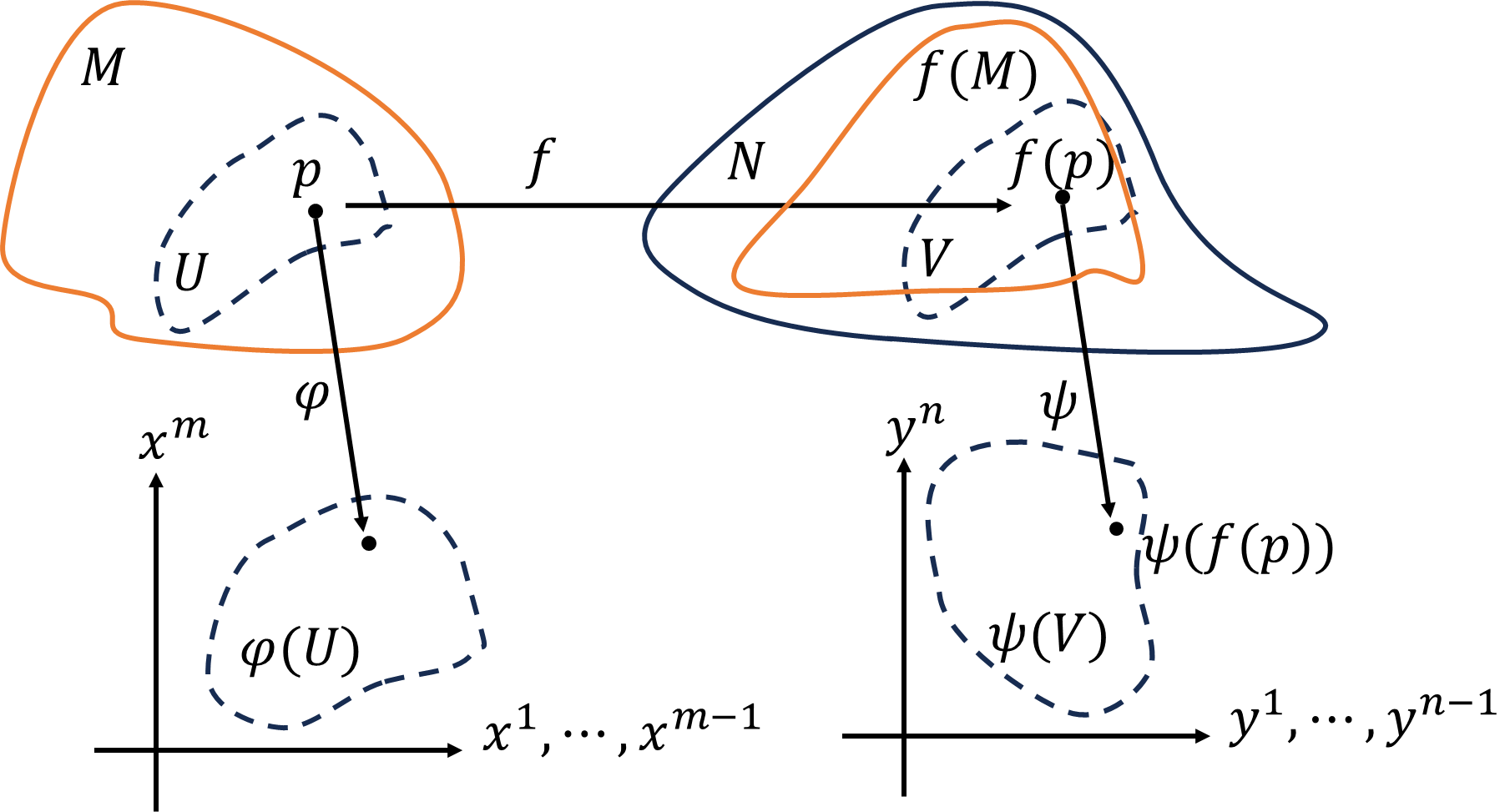
　この前使った図です。しかし今回は、\(\varphi^{-1}\circ f\circ\psi:\varphi(p)\to \psi(f(p))\)を\(\Psi\)と再定義します。つまり、\(\Psi:\varphi(U)\to\psi(V)\)です。\(\psi(V)\)上の関数\(h:\psi(V)\to\mathbb{R}\)の全微分は、 \[d:h\mapsto dh=\sum_{\nu=1}^n\frac{\partial h}{\partial y^\nu}dy^\nu\] 1特に次微分形式を与えます。特に\(\psi\)の座標変数の引き戻しは、 \[d:y^\nu\mapsto dy^\nu\] １次微分形式の基底を与えます。微分形式の引き戻しは、チェーンルールのようになされます。 \[\Psi^*(dh)=\sum_{\nu=1}^n\sum_{\mu=1}^m\frac{\partial h}{\partial y^\nu}\frac{\partial y^\nu}{\partial x^\mu}dx^\mu=\sum_{\mu=1}^m\frac{\partial(h\circ\Psi)}{\partial x^\mu}dx^\mu\] 特に\(dy^\nu\)の引き戻しは、 \[\Psi^*(dy^\nu)=\sum_{\mu=1}^m\frac{\partial( y^\nu\circ\Psi)}{\partial x^\mu}dx^\mu\] です。では、関数\(h:(y^1,\cdots,y^n)\to\mathbb{R}\)を\(M\)上に引き戻すと \[\Psi^*h=h\circ\Psi:(x^1,\cdots,x^m)\to\mathbb{R}\] さらに外微分をすると、 \[d(\Psi^*h)=\sum_{\mu=1}^m\frac{\partial(h\circ\Psi)}{\partial x^\mu}dx^\mu\] \(N\)上の関数は、引き戻ししてから外微分、外微分してから引き戻し、どちらも同じ結果になりました。 \[\begin{array}{ccc} h &\stackrel{\Psi^*}{\longrightarrow} & \Psi^*h\\ \downarrow{d} & & \downarrow{d}\\ dh&\stackrel{\Psi^*}{\longrightarrow} & d(\Psi^*h) \end{array}\]

\(N\)上のチャート\((\psi,V)\)において\(k\)次微分形式が、 \[\omega=\sum_{\nu_1\lt\cdots\lt\nu_k}\omega'_{\nu_1\cdots\nu_k}dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] と表せるとします。その外微分は、 \[d\omega=\sum_{\nu_1\lt\cdots\lt\nu_k}d\omega'_{\nu_1\cdots\nu_k}\wedge dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] \[=\sum_{\nu_1\lt\cdots\lt\nu_k}\delta^{\rho_1\cdots\rho_{k+1}}_{1\cdots k+1}d\omega'_{\nu_1\cdots\nu_k}(\Box_{\rho_1})dy^{\nu_1}(\Box_{\rho_2})\cdots dy^{\nu_k}(\Box_{\rho_{k+1}})\] \(\Psi\)を使って\(\varphi(U)\)上に引き戻してみましょう。1次微分形式\(d\omega'_{\nu_1\cdots\nu_k},dy^1,\cdots,dy^n\)をそれぞれ引き戻せばよいので、 \[\Psi^*(d\omega)=\sum_{\nu_1\lt\cdots\lt\nu_k}\delta^{\rho_1\cdots\rho_{k+1}}_{1\cdots k+1}\] \[\Psi^*(d\omega'_{\nu_1\cdots\nu_k})(\Box_{\rho_1})\Psi^*(dy^{\nu_1})(\Box_{\rho_2})\cdots \Psi^*(dy^{\nu_k})(\Box_{\rho_{k+1}})\] 引き戻し\(\Psi^*\)外微分は交換できるので、 \[=\sum_{\nu_1\lt\cdots\lt\nu_k}\delta^{\rho_1\cdots\rho_{k+1}}_{1\cdots k+1}d(\Psi^*\omega'_{\nu_1\cdots\nu_k})(\Box_{\rho_1})d(\Psi^*y^{\nu_1})(\Box_{\rho_2})\cdots d(\Psi^*y^{\nu_k})(\Box_{\rho_{k+1}})\] \[\Psi^*(d\omega)=\sum_{\nu_1\lt\cdots\lt\nu_k}d(\Psi^*\omega'_{\nu_1\cdots\nu_k})\wedge d(\Psi^*y^{\nu_1})\wedge\cdots\wedge d(\Psi^*y^{\nu_k})\] 今度は逆に引き戻ししてから外微分してみましょう。 \[\omega=\sum_{\nu_1\lt\cdots\lt\nu_k}\omega'_{\nu_1\cdots\nu_k}dy^{\nu_1}\wedge\cdots\wedge dy^{\nu_k}\] 関数\(\omega'_{\nu_1\cdots\nu_k}\)はそのまま引き戻して、座標変数\(y^\nu\)の外微分は１次微分形式\(dy^\nu\)で外微分と引き戻しを逆にできます。 \[\Psi^*\omega=\sum_{\nu_1\lt\cdots\lt\nu_k}(\Psi^*\omega'_{\nu_1\cdots\nu_k})\wedge d(\Psi^*y^{\nu_1})\wedge\cdots\wedge d(\Psi^*y^{\nu_k})\] これを外微分すれば、 \[d(\Psi^*\omega)=\sum_{\nu_1\lt\cdots\lt\nu_k}d(\Psi^*\omega'_{\nu_1\cdots\nu_k})\wedge d(\Psi^*y^{\nu_1})\wedge\cdots\wedge d(\Psi^*y^{\nu_k})\] 外微分と引き戻しどちらを先にやっても同じ結果が得られましたね。このようにして、\(k\)次微分形式についても引き戻しと外微分が交換できることが確認できました。多様体\(M,N\)について示しましたが、開被覆も多様体とみなせるので、\(U_1\cap U_2\neq\varnothing\)となる\(M,N\)を開被覆\(U_1,U_2\)に置き換えれば、\(f:p\to p\)の恒等写像となり、写像\(\Psi\)は座標変換となります。\(\Psi=\varphi^{-1}_1\circ f\circ\varphi_2=\varphi^{-1}_1\circ \varphi_2\)、多様体上での座標変換と外微分の順序を交換してもよいという証明でもあり、外微分が多様体上で、座標を気にせず使って問題ないということになります。 \[\begin{array}{ccc} \omega &\stackrel{\Psi^*}{\longrightarrow} & \Psi^*\omega\\ \downarrow{d} & & \downarrow{d}\\ d\omega&\stackrel{\Psi^*}{\longrightarrow} & d(\Psi^*\omega) \end{array}\]