楽しい科学（理論）チャンネル

　コンパクトで向き付け可能な多様体\(M\)上の\(m-1\)次微分形式\(\omega\)について、 \[\int_M d\omega=\int_{\partial M}\omega\] が成り立つ。

　向き付け可能というのは、座標変換のヤコビアンを正にするチャートをアトラスの中から選んで、\(M\)を覆うことができるということで、\(M\)を覆うチャートは自分で選んであげなくてはなりません。コンパクトは、有限個の開被覆で多様体を覆うことができることを意味します。１の分割は、多様体上の任意の点で開被覆の貼り合わせが有限個であるときに定義できます。

　初めに\(m=2\)のときでストークスの定理を証明して定理の雰囲気をつかみます。多様体はコンパクトと仮定したので、 \[M=U_1\cup\cdots\cup U_k\] となる、\(k\)個の開被覆\(U_1,\cdots, U_k\)を選べます。

　コンパクトで、向き付け可能な\(2\)次元多様体\(M\)の\(2-1\)次微分形式\(\omega\)は、例えばあるチャート、１の分割\((U_i,\varphi_i,\phi_i)\)で、 \[\omega=f_2dx^1+f_1dx^2\] とただの余接ベクトルで与えられます。余接ベクトルの成分の添え字が気持ち悪いかもしれませんが、\(m\)次元への拡張を見据えています。引き戻しを勉強したので、本来は、\(\varphi_i^*\omega\)などと書かなければいけない気がしますね！その直感はあっていますが、簡単に\(\omega\)と書くことにします。１次微分形式\(\omega\)の外微分を計算しますが、のちに積分するので１の分割もつけておきます。 \[d(\phi_i\omega)=\sum_{\mu_1=1}^2\frac{\partial \phi_if_2}{\partial x^{\mu_1}}dx^{\mu_1}\wedge dx^1+\sum_{\mu_2=1}^2\frac{\partial \phi_if_1}{\partial x^{\mu_2}}dx^{\mu_2}\wedge dx^2\] \(dx^i\wedge dx^i=0\)より、\(\mu_1=2,\mu_2=1\)以外の項は消えてしまいます。 \[d(\phi_i\omega)=\left((-1)^{1-1}\frac{\partial \phi_if_1}{\partial x^1}+(-1)^{2-1}\frac{\partial \phi_if_2}{\partial x^2}\right)dx^1\wedge dx^2\] \[=\sum_{\mu=1}^2(-1)^{\mu-1}\frac{\partial \phi_if_\mu}{\partial x^\mu}dx^1\wedge dx^2\] \(d(\phi_i\omega)\)を書く開被覆で積分しますが、開被覆が、多様体の境界\(\partial M\)を含む、含まないで場合分けが必要です。 \[\int_{U_i}d(\phi_i\omega)=\int_{\varphi_i(U_i)}\varphi_i^*d(\phi_i\omega)\] 本来\(\phi_i,\omega\)は多様体上で、定義されたものなので、\(x^1,x^2\)を使って表すために\(\varphi_i(U_i)\)に引き戻す(同相写像なので、押し出しでも間違いではないです。)表現が本当は正しいです。しかし、簡単に局所座標上でも単に\(\phi_i\)や、\(\omega\)と書くことにします。

(i)　開被覆が境界を含まないとき\(U_i\cap\partial M=\varnothing\)

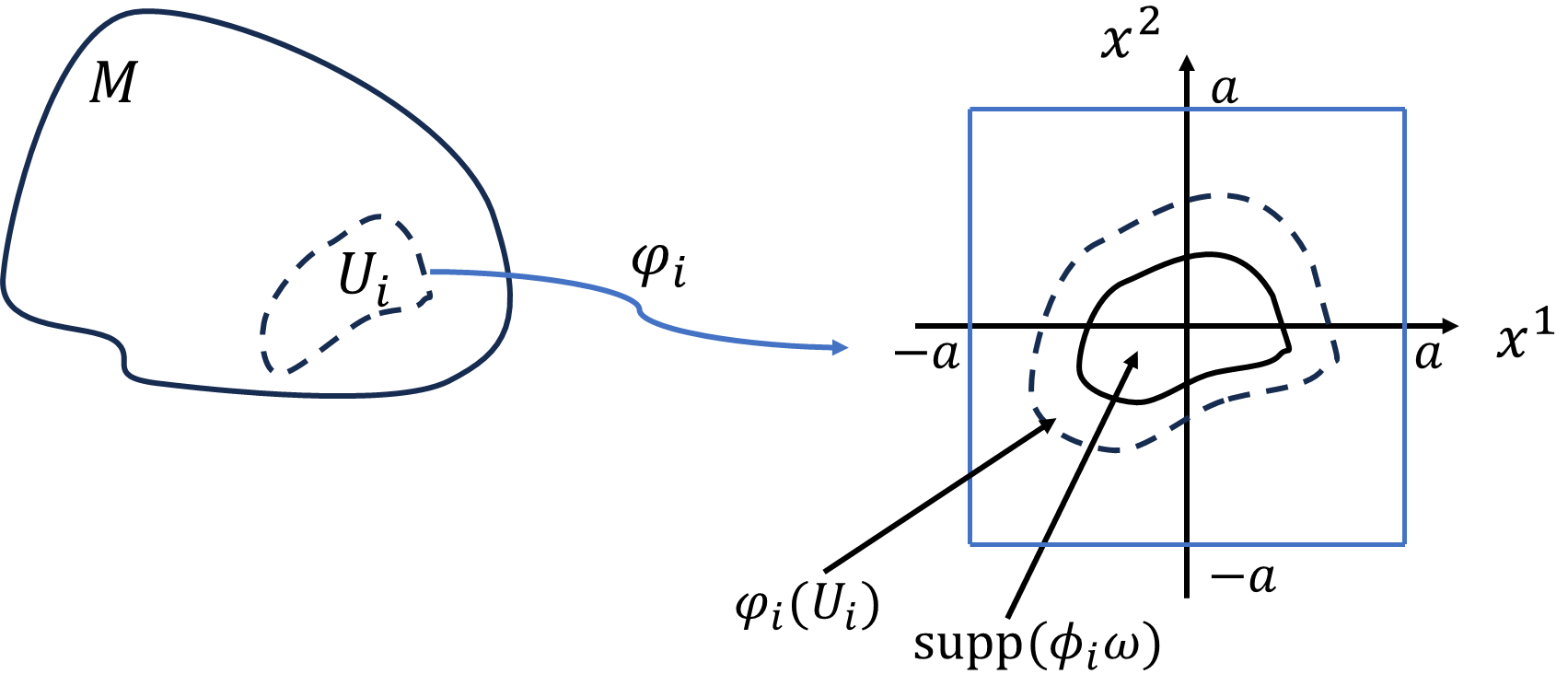
　\(U_i\)は、2次元ユークリッド空間上の開集合\(\varphi_i(U_i)\)と同相です。定数\(a\)を十分大きく取ることで、\(\varphi_i(U_i)\subset[-a,a]\times[-a,a]\)とすることができます。\(\phi_i\omega\gt0\)である、\(\mathrm{supp}(\phi_i\omega)\)の範囲での積分のみが積分値に寄与するので、積分範囲を広めに正方領域\([-a,a]\times[-a,a]\)でとっても良いです。 \[\int_{U_i}d(\phi_i\omega)=\int_{-a}^a\int_{-a}^a\sum_{\mu=1}^2(-1)^{\mu-1}\frac{\partial \phi_if_\mu}{\partial x^\mu}dx^1dx^2\] \[=\int_{-a}^a[\phi_if_1]_{-a}^adx^2-\int_{-a}^a[\phi_if_2]_{-a}^adx^1\] \(x^1,x^2=\pm a\)では1の分割\(\phi_i\)が０となるので、積分値は０となります。\(\int_Md\omega\)の積分値は、\(M\)の内部では0ということが分かりました。

(ii)　開被覆が境界を含むとき\(U_i\cap\partial M\neq\varnothing\)

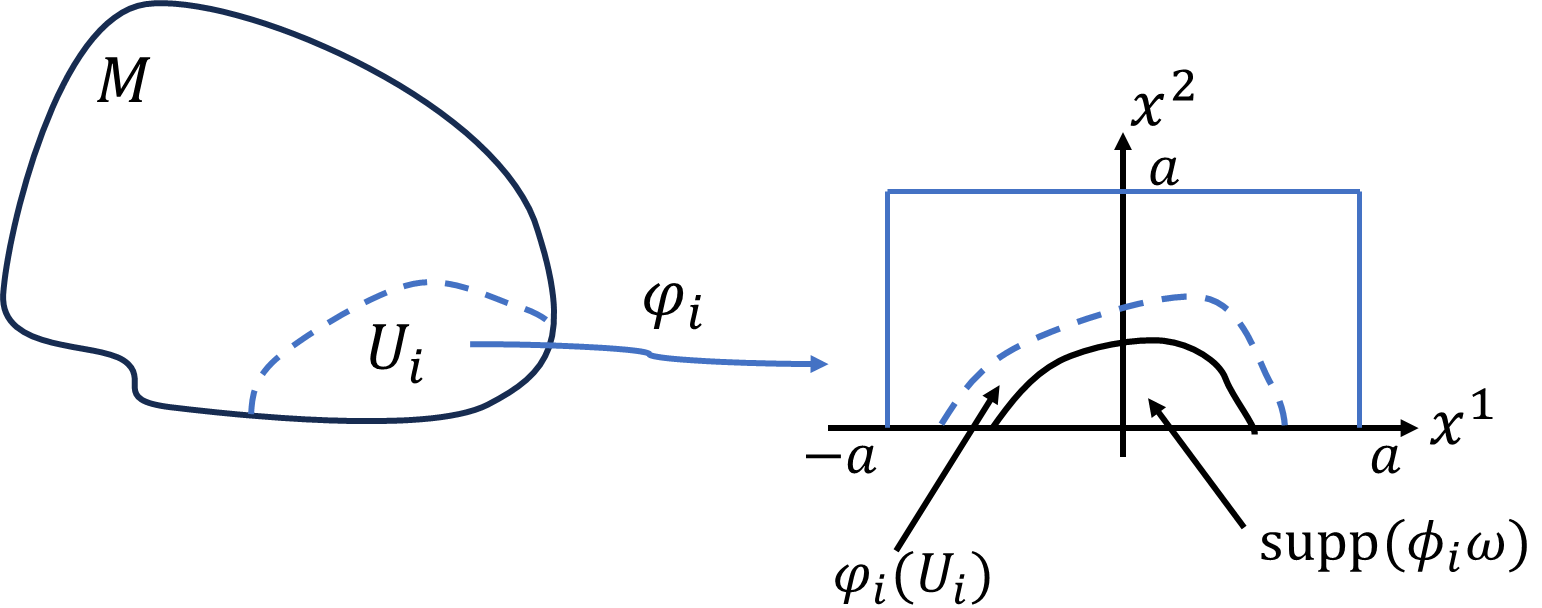
　\(U_i\)は、２次元上半空間上の開集合\(\varphi_i(U_i)\)と同相です。ただし、\(\varphi_i(\partial M\cap U_i)\)は、\(x^1\)軸上にあるように同相写像\(\varphi\)を調整します。\(\mathrm{supp}(\varphi_i\omega)\)の部分だけ積分値に寄与するので、\([-a,a]\times[0,a]\)まで積分範囲を広げても積分値は変わりません。依って、 \[\int_{U_i}d(\phi_i\omega)=\int_{-a}^a\int_0^a\sum_{\mu=1}^2(-1)^{\mu-1}\frac{\partial \phi_if_1}{\partial x^\mu}dx^1dx^2\] \[=\int_0^a[\phi_if_2]_{-a}^adx^2-\int_{-a}^a[\phi_i\omega]_{0}^adx^1\] \(x_1,x_2=\pm a\)のとき、１の分割が０なので、 \[=-\int_{-a}^a[\phi_i(x^1,x^2)\omega(x^1,x^2)]_{0}^adx^1=\int_{-a}^a\phi_i(x^1,0)\omega(x^1,0)dx^1\] この計算結果がどのように解釈されるかというと、

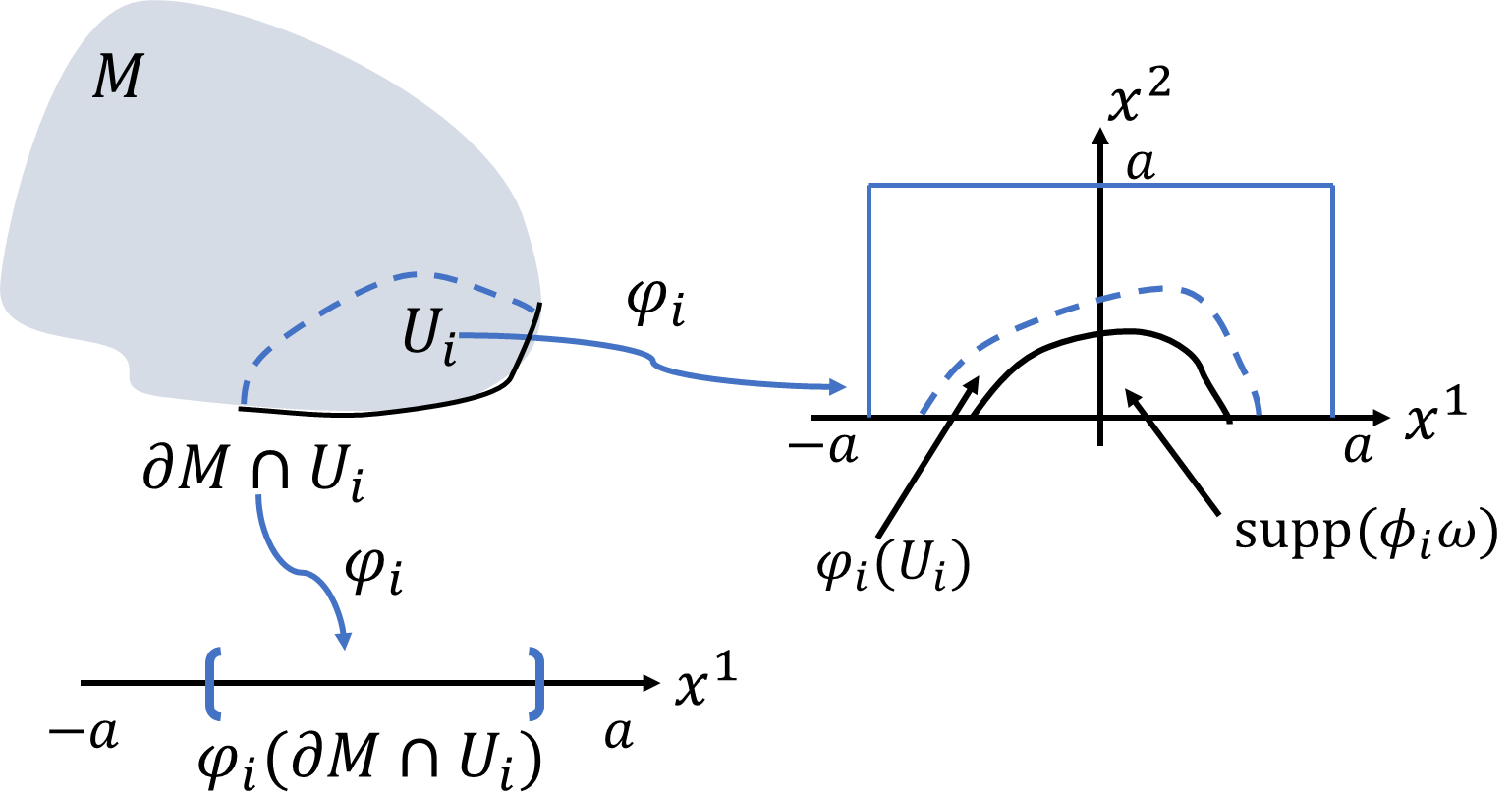
　\(x^2=0\)で固定して積分なので、\(x^1\)上での積分となります。多様体上では、\(\partial M\cap U_i\)の部分にあたりますね。つまり、 \[\int_{U_i}d(\phi_i\omega)=\int_{\partial M\cap U_i}\phi_i\omega\] と書くことができます。チャート\((U_i,\varphi_i)\)では、ストークスの定理を示すことに成功しました。 \[(\partial M\cap U_1)\cup\cdots \cup(\partial M\cap U_k)=\partial M\] である為、両辺を\(i=1\)から、\(i=k\)まで足したら、ストークスの定理が証明できそうです。しかし、各局所座標での積分値を足し合わせるときに、座標の向きというものを気にしなくてはなりません。\(M\)は向き付け可能と定義したので、座標変換のヤコビアンが正になる座標を取ることができますが、\(\partial M\)についても向き付け可能となっているでしょうか？そこは慎重に確認する必要があります。多様体\(\partial M\)を多様体と見た場合、\(\partial M\cap U_i\)は開被覆、\(\varphi_i\)(正しくは、\(\varphi_i|_{\partial M}\))は\(\varphi_i:\partial M\cap U_i\to \mathbb{R}^{m-1}\)であるため多様体\(\partial M\)の局所座標としても採用できます。採用しましょう！

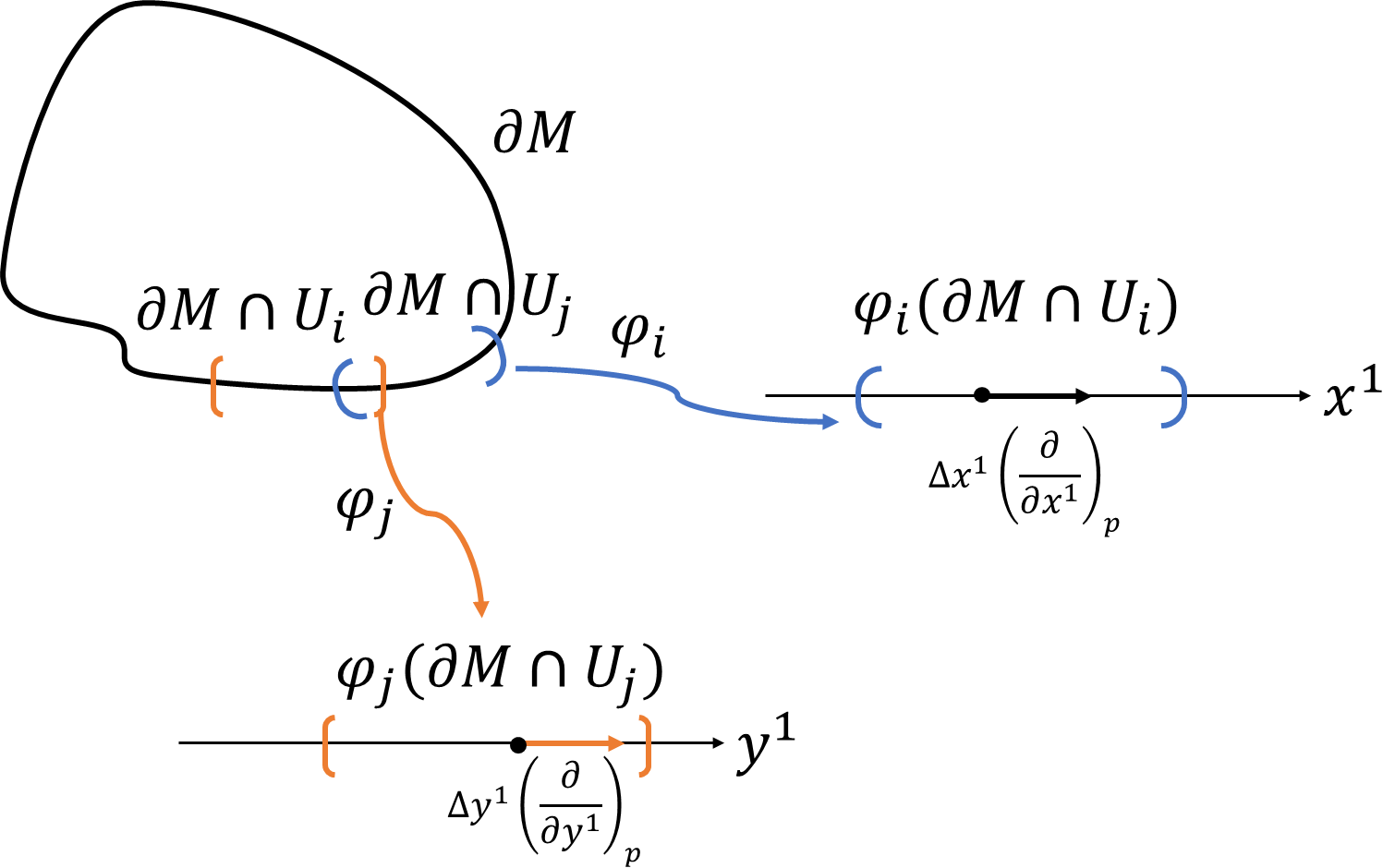
　1次元多様体\(\partial M\)上の重なりのある開被覆\(\partial M\cap U_i,\partial M\cap U_j\)について、それぞれの局所座標を\(\varphi_i|_{\partial M}=x^1,\varphi_j|_{\partial M}=y^1\) とします。座標変換\(\varphi_j|_{\partial M}\circ\varphi_i^{-1}|_{\partial M}\)によって、 \[y^1=y^1(x^1)\] と表すことができますね。座標変換のヤコビアンは、 \[J_{\partial M}=\frac{\partial y^1}{\partial x^1}=\frac{dy^1}{dx^1}\] となります。

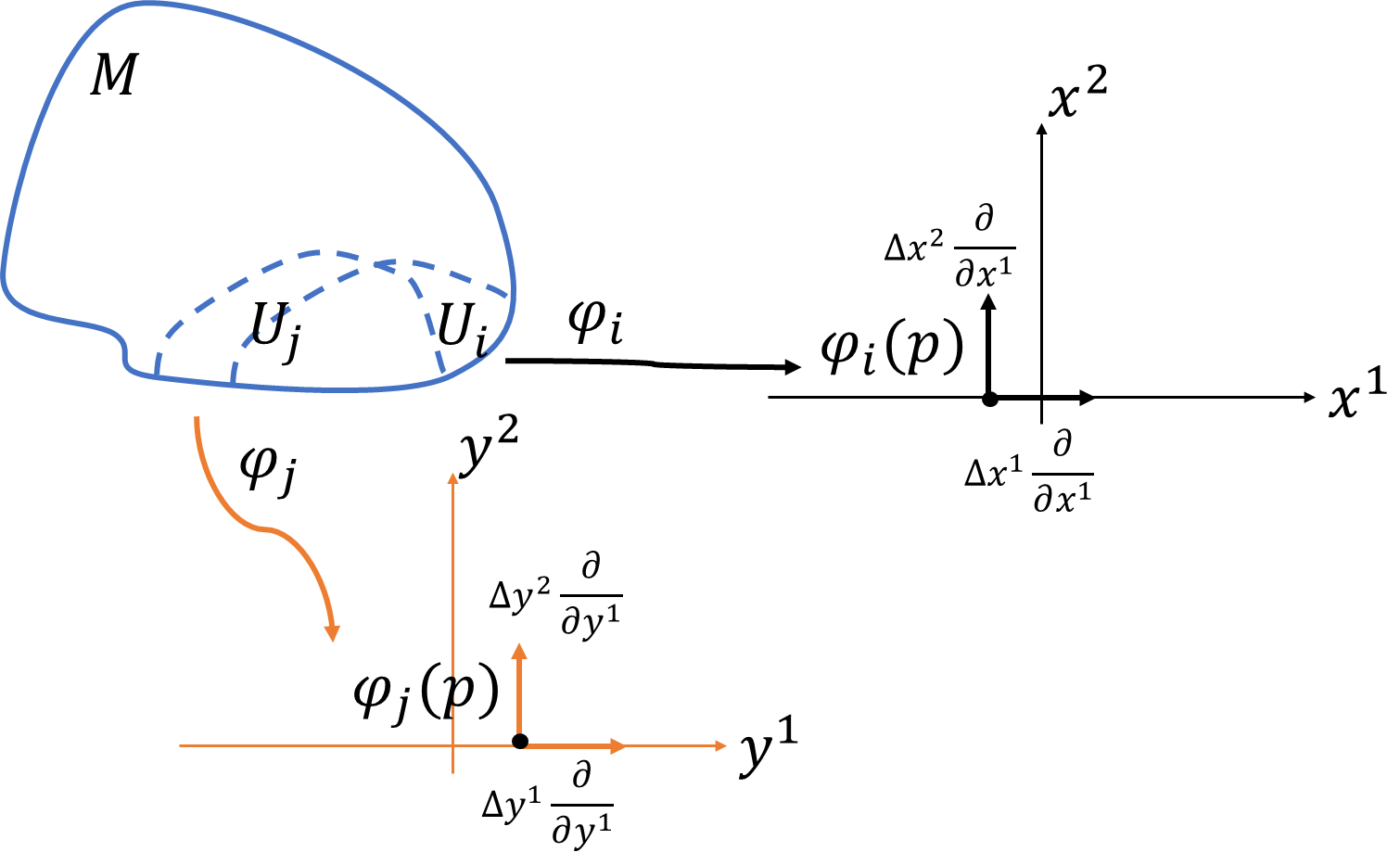
　多様体\(M\)の重なりのある開被覆\(U_i,U_j\)について、それぞれの局所座標を\(\varphi_i=(x^1,x^2),\varphi_j=(y^1,y^2)\)とすると、座標変換\(\varphi_j\circ\varphi_i^{-1}\)を \[y^1=y^1(x^1,0)\] \[y^2=y^2(x^1,x^2)\] と表すことにします。なぜ、\(y^1=y^1(x^1,x^2)\)でなく、\(y^1=y^1(x^1,0)\)としていいかというと、\(\partial M\)上の点はいかなる局所座標でも上半空間\(H^2=(x^1,x^2\ |\ x^2\ge0)\)の\(x^2=0\)に入っているからです。つまり、境界上の点は局所座標で、\((x^1,0)\)と表されます。それを座標変換\(\varphi_j\circ\varphi_i^{-1}\)した点を\(y^1(x^1,0)\)と表しているのです。座標変換のヤコビアンは、多様体\(M\)を向き付け可能としたので正で取ることができます。 \[J=\sum_{i=1}^2\sum_{j=1}^2\delta^{12}_{ij}\frac{\partial y^1}{\partial x^i}\frac{\partial y^2}{\partial x^j}=\frac{\partial y^1}{\partial x^1}\frac{\partial y^2}{\partial x^2}-\frac{\partial y^1}{\partial x^2}\frac{\partial y^2}{\partial x^1}\gt0\] \(y^1=y^1(x^1,0)\)は、\(x^2\)に依らないので、\(\frac{\partial y^1}{\partial x^2}=0\)、\(i=1\)の項だけ残ります。\(j=2\)と自動的に決まります。\(x^2\)軸、\(y^2\)軸いずれも局所座標上で\(\partial M\)から多様体内側向きを正と取った軸なので、変化量\(\varDelta x^2,\)が正なら、\(\varDelta y^2\)も正、\(\varDelta x^2,\)が負なら、\(\varDelta y^2\)も負となるはずです。つまり\(\frac{\partial y^2}{\partial x^2}\gt0\) \[\frac{\partial y^1}{\partial x^1}\underbrace{\frac{\partial y^2}{\partial x^2}}_{\gt0}\gt0\] \(M\)でヤコビアン\(J\gt0\)を正としたら、\(\partial M\)のヤコビアンも\(J_{\partial M}\gt0\)正となります！多様体の座標の向きが決まると、その境界の向きが決まるということですね。\(M\)で座標変換のヤコビアンが、任意の点で正なら、境界でもそうなっています。座標の向きが一致したチャートでアトラスを構成することで、各チャートでの積分値の和を考えることができます。以上から、向き付け可能でコンパクトな\(2\)次元多様体\(M\)と\(1\)次微分形式について、 \[\int_{M}d\omega=\sum_{i=1}^k\int_{U_i}\phi_id\omega=\sum_{i=1}^k\int_{U_i}\phi_id\omega+\sum_{i=1}^k\int_{U_i}d\phi_i\omega\] 1の分割の定義\(\sum_{i}\phi_i=1\)から、その全微分の和は、\(\sum_id\phi_i=d1=0\)です。つまり２項目は０で勝手に足しました。更にライプニッツ則から、\(d\phi_i\omega+\phi_id\omega=d(\phi_i\omega)\)なので、 \[\int_{M}d\omega=\sum_{i=1}^k\int_{U_i}d(\phi_i\omega)=\sum_{i=1}^k\int_{\partial M\cap U_i}\phi_i\omega=\int_{\partial M}\omega\] これが、\(m=2\)の時のストークスの定理です。教本によっては、包含写像\(\iota:\partial M\to M\)を用いて、\(\int_Md\omega=\int_{\partial M}\iota^*\omega\)などと書いてもいいでしょう。包含写像を使って、微分形式を境界上に引き戻しているので、\(\partial M\)上の微分形式を微分していることを意味します。例として、電流\(I\)と磁場\(H\)の関係を見ていきます。円盤\(D\)と円周\(S^1\)を \[D=\{(r,\theta)\ |\ 0\le r\le 1,\ 0\le\theta\lt2\pi\}\] \[S^1=\{(r,\theta)\ |\ r=1,\ 0\le\theta\lt2\pi\}\] とします。円周\(S^1\)から円盤\(D\)への包含写像を\(\iota:S^1\to D\)とします。\(D\)上の1次微分形式 \[H=\vec{H}\cdot d\vec{r}=H_r(r,\theta)dr+H_\theta(r,\theta) d\theta\] の外微分は、 \[dH=\left(\frac{\partial H_\theta(r,\theta)}{\partial r}-\frac{\partial H_r(r,\theta)}{\partial \theta}\right)dr\wedge d\theta\] 一方包含写像\(\iota:S^1\to D\)によって\(H\)を\(S^1\)上に引き戻すと、 \[\iota^*H=H_r(1,\theta)\frac{dr}{d\theta}d\theta+H_\theta(1,\theta)\frac{d\theta}{d\theta}d\theta=H_\theta(1,\theta)d\theta\] \(r,\theta\)は独立した変数で、\(\frac{dr}{d\theta}=0\)です。\(S^1\)上での磁場\(H\)の積分は、\(D\)を通過する電流\(I\)であるとアンペールの法則によって決まっています。 \[I=\int_{S^1}\iota^*H=\int_0^{2\pi}H_\theta d\theta\] ストークスの定理から、 \[\int_{D}dH=\int_{S^1}\iota^*H=I\] 電流\(I\)と外微分された磁場\(H\)を\(D\)上で積分した値は一致します。外微分の計算については説明しましたが、一例として1次元多様体\(H\)が円状の磁場を表している場合、その外微分\(dH\)は電流と同じ向きの２次微分形式というイメージを持つとよいでしょう。\(\theta\)軸上の集合\([0,2\pi)\)は\(0,2\pi\)で繋がっていないので\(S^1\)と同相でないです。本当は少なくとも開被覆を２つ取って積分を２つに分けなければなりません。