楽しい科学（理論）チャンネル

　コンパクトで向き付け可能な多様体\(M\)上の\(m-1\)次微分形式\(\omega\)について、 \[\int_M d\omega=\int_{\partial M}\omega\] が成り立つ。

　向き付け可能で、コンパクトな3次元多様体\(M\)の2次微分形式\(\omega\)について、多様体はコンパクトなので、有限個の開被覆で覆うことができます。 \[M=U_1\cup\cdots\cup U_k\] 向き付け可能なので、座標変換のヤコビアンが正となるチャート\((U_i,\varphi_i)\)のみでアトラスを構成します。1の分割を\(\phi_i\)とします。ある局所座標\(\varphi_i=(x^1,x^2,x^3)\)で微分形式が、 \[\phi_i\omega=\phi_if_3dx^1\wedge dx^2+\phi_if_2dx^1\wedge dx^3+\phi_if_1dx^2\wedge dx^3\] と表せるとしましょう。後で各チャートでの積分値の総和を取るので、あらかじめ１の分割もかけてあります。外微分を取ると、 \[d(\phi_i\omega)=\sum_{\mu_1=1}^3\frac{(\partial\phi_if_3)}{\partial x^{\mu_1}}dx^{\mu_1}\wedge dx^1\wedge dx^2\] \[+\sum_{\mu_2=1}^3\frac{(\partial\phi_if_2)}{\partial x^{\mu_2}}dx^{\mu_2}\wedge dx^1\wedge dx^3\] \[+\sum_{\mu_3=1}^3\frac{(\partial\phi_if_1)}{\partial x^{\mu_3}}dx^{\mu_3}\wedge dx^2\wedge dx^3\] くさび積の交代性から、余接ベクトルの成分が重複するとその項は０となるので、\((\mu_1,\mu_2,\mu_3)=(3,2,1)\)の項だけ残ります。 \[d(\phi_i\omega)=\left((-1)^{1-1}\frac{(\partial\phi_if_1)}{\partial x^1}+(-1)^{2-1}\frac{(\partial\phi_if_2)}{\partial x^2}\right.\] \[\left.(-1)^{3-1}\frac{(\partial\phi_if_3)}{\partial x^3}\right)dx^1\wedge dx^2\wedge dx^3\] \(m=2\)で証明した時に比べ、２項から、３項の総和になり、最後に\(\wedge dx^3\)になっただけです。規則性が見えたので、\(m\)次元多様体にも簡単に拡張できそうです。 \[d(\phi_i\omega)=\sum_{\mu=1}^3(-1)^{\mu-1}\frac{\partial(\phi_if_\mu)}{\partial x^\mu}dx^1\wedge dx^2\wedge dx^3\] ここから境界を含むか含まないかで場合分けが必要になります。

(i)　\(U_i\cap\partial M=\varnothing\)となるチャート、１の分割の組\((U_i,\varphi_i,\phi_i)\)の時、

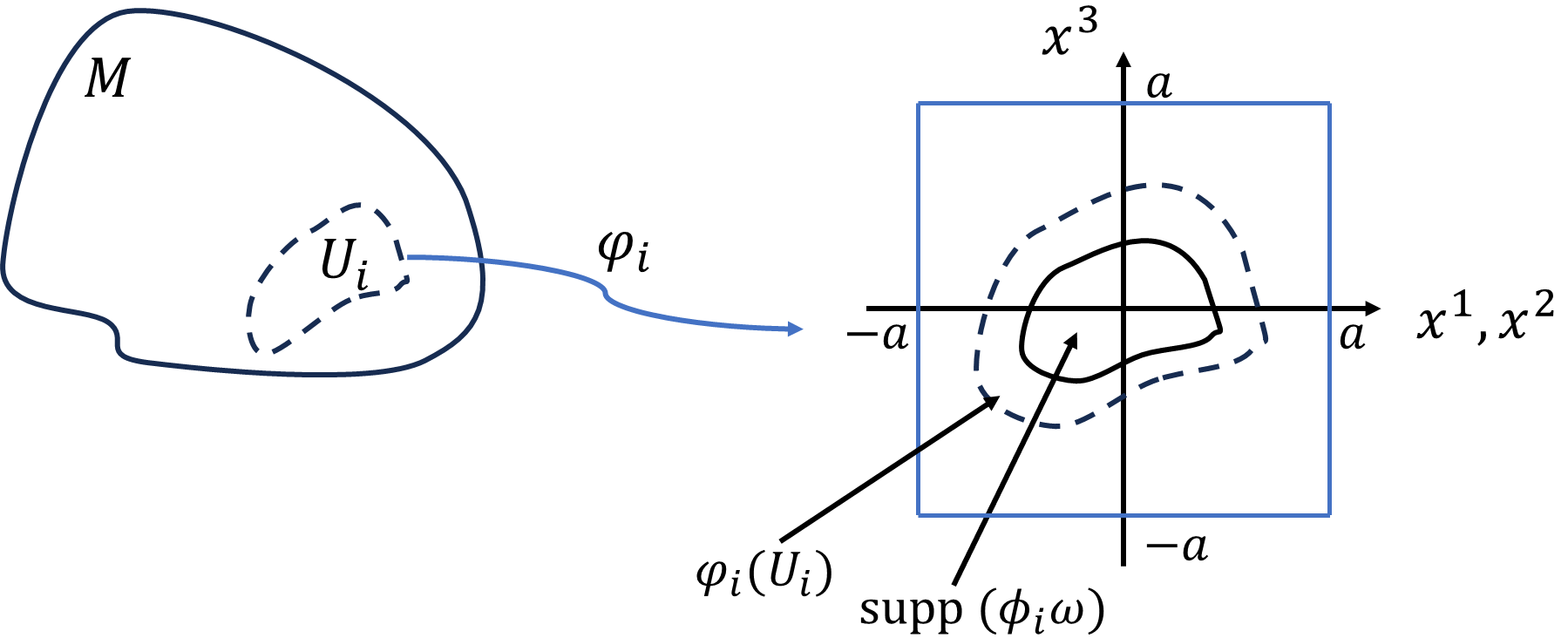
　局所座標\(\varphi_i=(x^1,x^2,x^3)\)上での、\(d(\phi_i\omega)\)の積分範囲は、\(\varphi_i(U_i)\)ですが、\(\mathrm{supp}(\varphi^{-1*}(\phi_i\omega))\subset\varphi_i(U_i)\)のみ積分の値に寄与するので、十分に大きい定数\(a\)について、積分範囲を\(\varphi_i(U_i)\subset [-a,a]^3\)の立方領域まで、広げても積分値は変わりません。 \[\int_{U_i}d(\phi_i\omega)=\sum_{\mu=1}^3(-1)^{\mu-1}\int_{-a}^a\int_{-a}^a\int_{-a}^{a}\frac{\partial(\phi_if_\mu)}{\partial x^\mu}dx^1dx^2dx^3\] \(\mu=1\)の項は、 \[\int_{-a}^a\int_{-a}^a\int_{-a}^{a}\frac{\partial(\phi_if_1)}{\partial x^1}dx^1dx^2dx^3=\int_{-a}^a\int_{-a}^a[\phi_if_1]_{-a}^adx^2dx^3\] \(x^1=\pm a\)で\(\phi_i=0\)なので、\(\mu=1\)の時の項は積分すると０です。他の項も同様に０となる為、 \[\int_{U_i}d(\phi_i\omega)=0\] 境界を含まなければ、積分の値は０です。

(ii)　\(U_i\cap\partial M\neq\varnothing\)となるチャート、１の分割の組\((U_i,\varphi_i,\phi_i)\)の時、

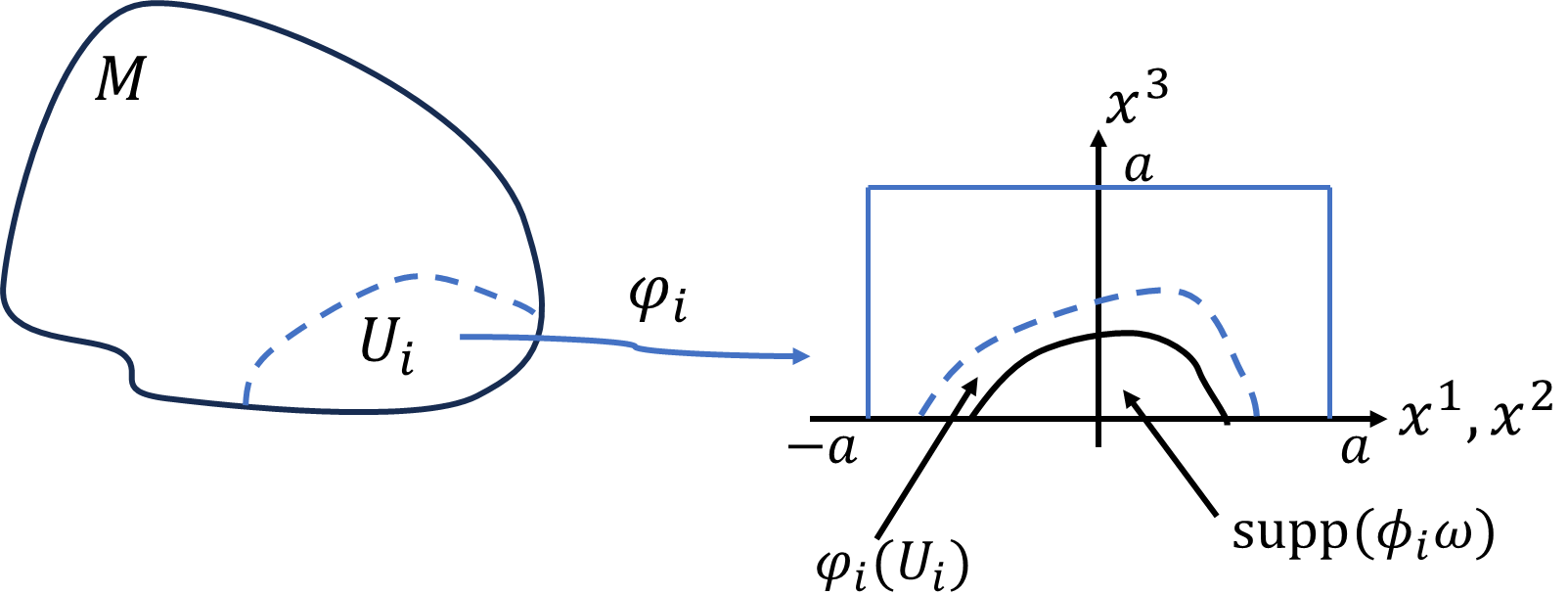
　十分大きな定数\(a\)を用いることで、領域\([-a,a]\times[-a,a]\times[0,a]\)で、\(\varphi_i\)で、\(\varphi_i(U_i)\)を覆うことができます。\(\mathrm{supp}(\phi_i\omega)\)だけが積分に寄与して、その外での積分は０になるので、領域\([-a,a]\times[-a,a]\times[0,a]\)まで積分範囲を拡張して問題ないです。 \[\int_{U_i}d(\phi_i\omega)=\sum_{\mu=1}^3(-1)^{\mu-1}\int_{-a}^a\int_{-a}^a\int_{0}^a\frac{\partial(\phi_if_\mu)}{\partial x^\mu}dx^1dx^2dx^3\] \(x^\mu=\pm a\)のとき\(\phi_i\)が０になるので、3項目だけ残ります。 \[\int_{U_i}d(\phi_i\omega)=\int_{-a}^a\int_{-a}^a[\phi_i(x^1,x^2,x^3)f_3(x^1,x^2,x^3)]_0^adx^1dx^2\] これもやはり、\(x^3=a\)の時０なので、 \[\int_{U_i}d(\phi_i\omega)=-\int_{-a}^a\int_{-a}^a\phi_i(x^1,x^2,0)f_3(x^1,x^2,0)dx^1dx^2\] 　\(x^3=0\)は\(\partial M\)に対応しているので、境界上の積分であることは確かです。しかし、マイナスが余計についているように見えますが、このマイナスは必須です。この式をベクトルっぽく解釈しようとすれば、

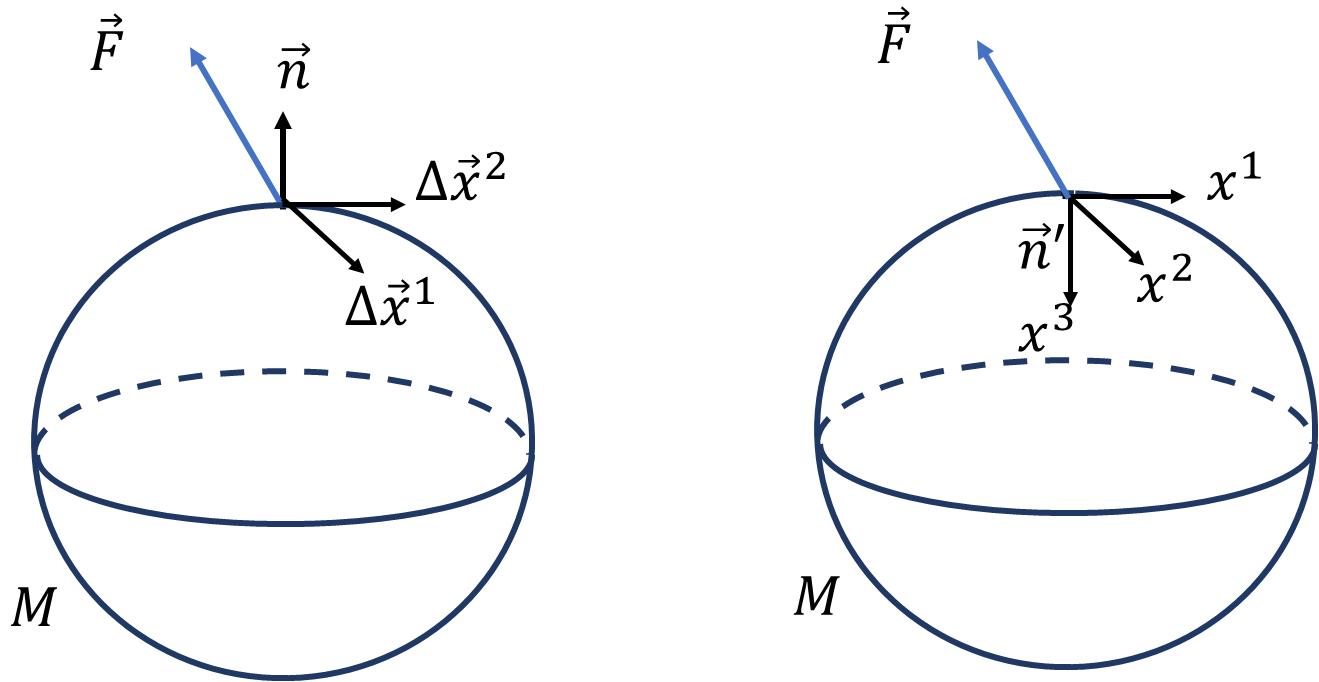
３次元空間の図形\(M\)の境界\(\partial M\)は曲面で、法線ベクトル単位\(\vec{n}\)は\(M\)の外側向きにとるのが普通です。\(\partial M\)の表面は、外側と決められています。ベクトル場\(\vec{F}\)と内積を取って、\(\vec{F}\cdot\vec{n}\)面積要素をかけて、\(M\)上で足し合わせる計算を面積分\(\int_{\partial M}\vec{F}\cdot\vec{n}dS\)と呼びます。この視点から上半空間は、図形\(M\)の内側に第３軸を取るので、\(\partial M\)の法線単位ベクトル\(\vec{n}'\)は、従来の面積分と逆です。 \[\int_{\partial M}\vec{F}\cdot\vec{n}dS=-\int_{\partial M}\vec{F}\cdot\vec{n}'dS\] 今やってきた計算は、上半空間を使った計算で、多様体と接する方の境界面を表としています。\(\vec{n}'\)を使って面積分を計算しているので、 \[\int_{U_i}d(\phi_i\omega)=\int_{\partial M\cap U_i}\phi_i\omega\] 面積分はマイナスの符号も巻き込んで、面積分と定義します。別に面積分を多様体の外向きを表面と定義しなければ、 \[\int_{U_i}d(\phi_i\omega)=-\int_{\partial M\cap U_i}\phi_i\omega\] であり、ストークスの定理は、 \[\int_{M}d\omega=(-1)^{m}\int_{\partial M}\omega\] ただし、\(m\)が奇数の場合は、\(\partial M\)の多様体と接する面が表向き、としてもいいです。 \(M\)の座標の向きが決まれば、\(\partial M\)の座標の向きが決まることも見ていきましょう。

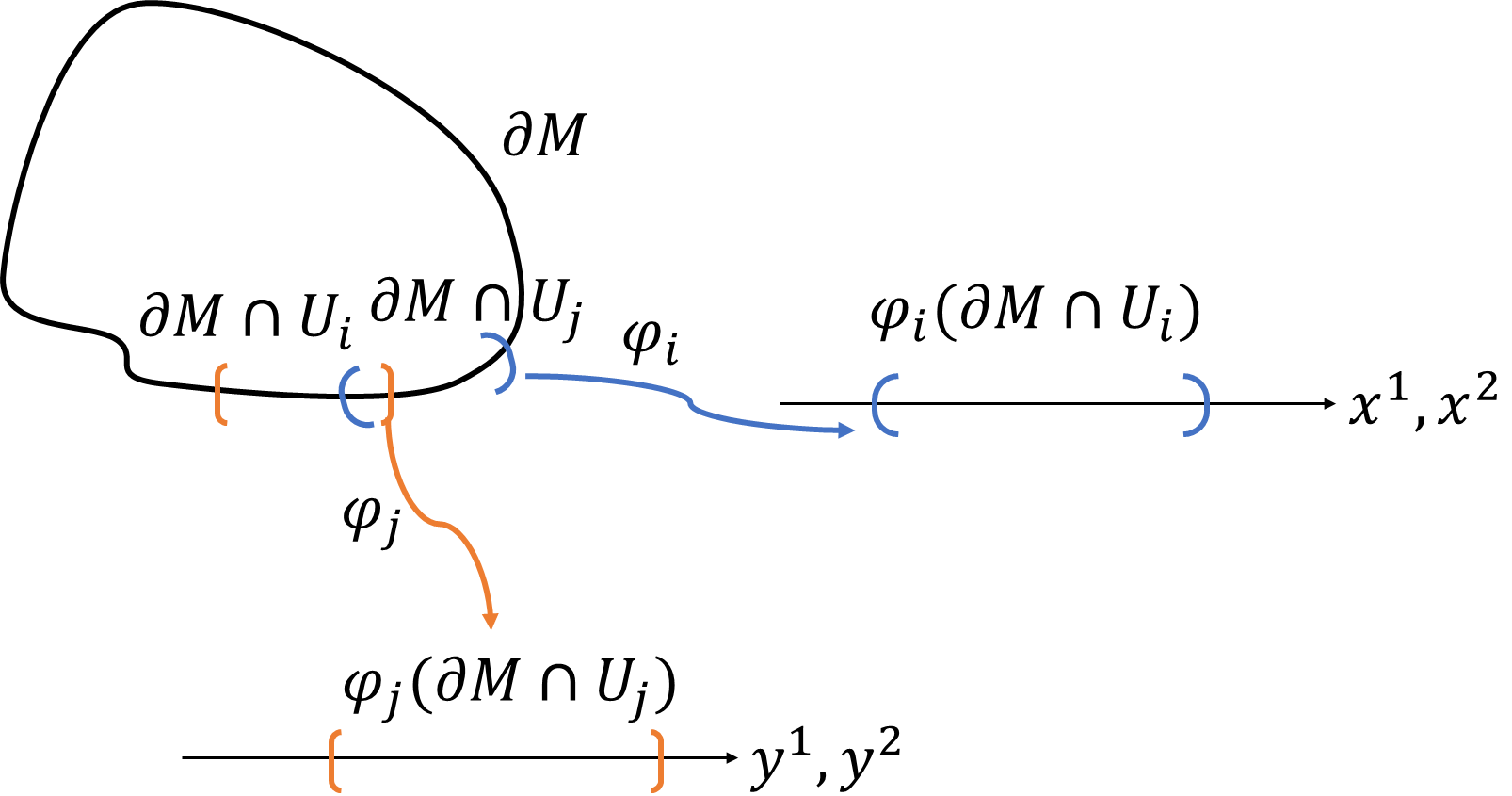
　\(\partial M\)を多様体だという見方をしてみます。\(\partial M\)のアトラスは、\(\{\partial M\cap U_i,\varphi_i|_{\partial M}\}_{i=1}^k\) もともとの多様体\(M\)のアトラス\(\{U_i,\varphi_i\}_{i=1}^k\)から境界\(\partial M\)に制限したものを採用します。\(\partial M\)は\(2\)次元多様体なので、局所座標は、\(2\)次元ユークリッド空間になります。境界部分で重なりを持つ開被覆\(\partial M\cap U_i,\partial M\cap U_j\)の局所座標をそれぞれ\(\varphi_i|_{\partial M}=(x^1,x^2),\varphi_j|_{\partial M}=(y^1,y^2)\)とします。座標変換を \[y^j=y^j(x^1,x^2),\ (j=1,2)\] と表すことにすれば、座標変換のヤコビアンは、 \[J_{\partial M}=\sum_{\mu_1=1}^2\sum_{\mu_2=1}^2\delta_{12}^{\mu_1\mu_2}\frac{\partial y^1}{\partial x^{\mu_1}}\frac{\partial y^2}{\partial x^{\mu_2}}\] です。多様体\(M\)の重なりをもつ開被覆\(U_i,U_j\)の座標変換は \[y^j=y^j(x^1,x^2,0),\ (j=1,2)\] \[y^3=y^3(x^1,x^2,x^3)\] とすることができます。\(y^1,y^2\)は、\(x^3\)を用いずとも上半空間\(H^3=(x^1,x^2,x^3\ |\ x^3\ge0)\)のうち、\(x^3=0\)とした、\(\mathbb{R}^2\)空間同士の座標変換で決まります。一方、\(y^3\)は\(H^3\)同士の座標変換で得られるので、\(x^3\)にも依ります。\(M\)は向き付け可能なので、座標変換のヤコビアンを正にとれます。 \[J=\sum_{\mu_1=1}^3\sum_{\mu_2=1}^3\sum_{\mu_3=1}^3\delta_{123}^{\mu_1\mu_2\mu_3}\frac{\partial y^1}{\partial x^{\mu_1}}\frac{\partial y^2}{\partial x^{\mu_2}}\frac{\partial y^3}{\partial x^{\mu_3}}\gt0\] \(y^1,y^2\)は、\(x^3\)に依らないので、\(\mu_1=\mu_2=3\)となる項は０となり、\(\mu_3\)は自動的に\(\mu_3=3\)と決まります。 \[J=\sum_{\mu_1=1}^2\sum_{\mu_2=1}^2\delta_{123}^{\mu_1\mu_23}\frac{\partial y^1}{\partial x^{\mu_1}}\frac{\partial y^2}{\partial x^{\mu_2}}\frac{\partial y^3}{\partial x^{3}}\gt0\] また、\(x^3,y^3\)軸はともに多様体内側を向いた軸なので、\(\frac{\partial x^3}{\partial y^3}\gt0\)です。δの記号の\(\delta_{123}^{\mu_1\mu_23}\)の3の部分は、交換されず、置換に\(\mu_1,\mu_2\)の置換に影響されないので、\(\delta_{123}^{\mu_1\mu_23}=\delta_{12}^{\mu_1\mu_2}\) \[J=J_{\partial M}\underbrace{\frac{\partial y^3}{\partial x^{3}}}_{\gt0}\gt0\] はいこれで、多様体の向きが正なら、境界の向きが正となりますね。正の向きを取れば、チャートの積分値の総和が多様体上の積分として意味を持ちます。\(\sum_id\phi_i=d(\sum\phi_i)=d1=0\)を活用して、 \[\int_Md\omega=\sum_{i=1}^k\int_{U_i}\phi_id\omega=\sum_{i=1}^k\int_{U_i}d(\phi_i\omega)\] \[=\sum_{i=1}^k\int_{\partial M\cap U_i}\phi_i\omega=\int_{\partial M}\omega\] \(m=3\)の時ストークスの定理を示すことができました。これ以上次元が高いと視覚化できませんが、きっとうまくいっていることでしょう。

　もう今までで、話したいことは話しました。ここにはよく教本に載っていそうなストークスの定理の証明をちょいと書いておきます。

　向き付け可能で、コンパクトな\(m\)次元多様体\((M,\mathcal{S})\)について、\(M\)はコンパクトなので、有限個の開被覆\(U_1,\cdots,U_k\)で多様体\(M\)を被覆できます。更に、向き付け可能としたので、局所座標間のヤコビアン\(J\)が正になるようにアトラスを構成します。 \[\mathcal{S}=\{U_i,\varphi_i\}_{i=1}^k\] 多様体\(M\)上の\(m-1\)次微分形式\(\omega\)はある局所座標\(\varphi_i=(x^1,\cdots,x^m)\)で、 \[\omega=\sum_{\nu_1\lt\cdots\lt\nu_{m-1}}\omega_{\nu_1\cdots\nu_{m-1}}dx^{\nu_1}\wedge\cdots\wedge x^{\nu_{m-1}}\] と表されます。この後の計算の都合で、少し書き換えます。微分形式\(\omega\)の基底部分は、\(m\)次微分形式の基底\(dx^1\wedge\cdots\wedge dx^m\)から、余接ベクトル\(dx^\mu,\ (\mu=1,2\cdots,m)\)が１つ欠けたものともとらえられます。更に成分の部分\(\omega_{\nu_1\cdots\nu_{m-1}}\)をもっと単純に表記して、 \[\omega=\sum_{\mu=1}^mf_{\mu}dx^1\wedge\cdots\wedge\mathop{dx^\mu}^{\times}\wedge\cdots\wedge dx^m\] と表すことにします。\(\mathop{dx^\mu}^{\times}\)はその余接ベクトルが微分形式の基底に含まれないことを意味します。後で多様体上の積分値を考えたいので、多様体上の関数である1の分割\(\phi_i\)もかけて外微分を取ります。局所座標に引き戻した１の分割も同様に\(\phi_i\)と書くことにします。\(\phi_i\omega\)の外微分は、 \[d(\phi_i\omega)=\sum_{\mu=1}^m\sum_{\nu=1}^m\frac{\partial \phi_if_{\mu}}{\partial x^\nu} dx^\nu \wedge dx^1\wedge\cdots\wedge\mathop{dx^\mu}^{\times}\wedge\cdots\wedge dx^m\] 交代性より、\(\mu=\nu\)以外の項は0となります。 \[d(\phi_i\omega)=\sum_{\mu=1}^m\frac{\partial \phi_if_{\mu}}{\partial x^\mu} dx^\mu \wedge dx^1\wedge\cdots\wedge\mathop{dx^\mu}^{\times}\wedge\cdots\wedge dx^m\] 一番左の\(dx^\mu\)を欠落している場所まで移動させます。\(\mu=1\)の時は移動なしで符号は正、\(\mu=2\)の時は、1度だけ交換して符号は負、、、と続けてすべての項について行えば、 \[d(\phi_i\omega)=\sum_{\mu=1}^m(-1)^{\mu-1}\frac{\partial \phi_if_{\mu}}{\partial x^\mu}dx^1\wedge\cdots\wedge dx^m\] これをチャート上で積分したいのですが、場合分けが必要です。

(i)　\(\partial M\cap U_i=\varnothing\)の場合

　\(\mathrm{supp}(\phi_i\omega)\subset\varphi_i(U_i)\subset[-a,a]^m\)となる領域\([-a,a]^m\)を取ります。もともとの積分範囲は、\(\varphi_i(U_i)\)ですが、\(\mathrm{supp}(\phi_i\omega)\)以外の領域では、積分値が0となるので、\([-a,a]^m\)まで積分範囲を広げて問題ないです。 \[\int_{U_i}d(\phi_i\omega)=\int_{\varphi_i(U_i)}\sum_{\mu=1}^m(-1)^{\mu-1}\frac{\partial \phi_if_{\mu}}{\partial x^\mu}dx^1\cdots dx^m\] \[=\sum_{\mu=1}^m(-1)^{\mu-1}\int_{-a_1}^{a_1}\cdots\int_{-a_m}^{a_m}\frac{\partial \phi_if_{\mu}}{\partial x^\mu}dx^1\cdots dx^m\] インテグラルが何個あるかわかりずらいので、定数\(a\)に番号を振りました。正方領域なのでどの順で積分しても問題ありません。各項の\(\mu\)番目の積分を先に行います。 \[=\sum_{\mu=1}^m(-1)^{\mu-1}\int_{-a_1}^{a_1}\cdots\mathop{\int_{-a_\mu}^{a_\mu}}^{\times}\cdots\int_{-a_m}^{a_m}[\phi_if_{\mu}]_{-a}^adx^1\cdots \mathop{dx^\mu}^{\times}\cdots dx^m\] \(x^\mu=\pm a\)は、\(\mathrm{supp}\phi_i\)の外なので、\(\phi_i=0\)となり、すべての項が０となります。以上から、境界をふくまないチャートで、 \[\int_{U_i}d(\phi_i\omega)=0\] となります。

(ii)　\(\partial M\cap U_i\neq\varnothing\)の場合

　境界を含む開被覆\(U_i\)は同相写像\(\varphi_i\)で上半空間 \[H^m=\{x^1,\cdots,x^m\ |\ x^m\ge0\}\] 内の開集合\(\varphi_i(U_i)\)とに写されます。ただし、境界部分\(\partial M\cap U_i\)は、\(x^m=0\)の\(m-1\)次元ユークリッド空間\(\mathbb{R}^{m-1}\)内の開集合\(\varphi_i(\partial M\cap U_i)\)に同相とします。積分範囲は、\(\varphi_i(U_i)\)ですが、\(\mathrm{supp}\phi_i\subset \varphi_i(U_i)\)なので、積分範囲を\([-a,a]^{m-1}\times[0,a]\)まで積分範囲を広げても積分値は変わらないので、 \[\int_{U_i}d(\phi_i\omega)=\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}\int_{0}^{a_m}\sum_{\mu=1}^m(-1)^{\mu-1}\frac{\partial \phi_if_{\mu}}{\partial x^\mu}dx^1\cdots dx^m\] \[=\sum_{\mu=1}^m(-1)^{\mu-1}\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}\int_{0}^{a_m}\frac{\partial \phi_if_{\mu}}{\partial x^\mu}dx^1\cdots dx^m\] \(\mu=1,\cdots,m-1\)の項では、場合分け(i)と同じ理由から積分値は、0となります。\(\mu=m\)の項だけ残ります。 \[\int_{U_i}d(\phi_i\omega)=\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}\int_{0}^{a_m}(-1)^{m-1}\frac{\partial \phi_if_{m}}{\partial x^m}dx^1\cdots dx^m\] \(\int_{0}^{a_m}\Box dx^m\)の積分だけやります。ただし、(i)と同じ理由で、不定積分後\(x^m=a_m\)を代入した項は０となります。 \[\int_{U_i}d(\phi_i\omega)=(-1)^{m-1}\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}[\phi_if_{m}]_{x^m=0}^{x^m=a}dx^1\cdots dx^m\] \[=(-1)^m\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}\iota^*(\phi_if_m)dx^1\cdots dx^m\] \(f_m(x^1,\cdots,x^{m-1},0)\)と書きたかったですが、長いので、境界から多様体への写像\(\iota:\partial M\to M\)を用いて、引き戻しで表現しました。 \(m=2,3\)の時の慣習にしたがい、\(m\)が偶数次元であれば、座標の向きを正、\(m\)が奇数次元であれば、座標の向きが負とすれば、左辺は\(\partial M\cap U_i\)上の積分となるので、 \[\int_{U_i}d(\phi_i\omega)=(-1)^{m-1}\int_{-a_1}^{a_1}\cdots\int_{-a_{m-1}}^{a_{m-1}}[\phi_if_{m}]_{x^m=0}^{x^m=a}dx^1\cdots dx^m\] \[=\int_{\partial M\cap U_i}\omega\] 多様体の次元によって、座標の向きを変えるのが自然だと感じなければ、多様体の座標の向きを次元に依らず一貫させて、定理の方を\(\int_{M}d\omega=(-1)^m\int_{\partial M}\omega\)と書き換えてもよいと思います。(しかし、そのように書いている文献を持っていません！)各チャートの積分値を足し合わせる前に座標の向きがそろっていることを確認しなければなりません。\(M\)は向き付け可能なため、座標の向きを正にとって、左辺\(\int_{U_i}d(\phi_i\omega)\)の総和は意味を持ちます。右辺\(\int_{\partial M\cap U_i}\omega\)の総和が、\(\partial M\)上の積分値としての意味を持つためには、\(\partial M\)の座標変換におけるヤコビアンも正であることを示さなくてはなりません。\(\partial M\)で共通部分を持つ開被覆\(U_i,U_j\)の局所座標をそれぞれ、\(\varphi_i=(x^1,\cdots,x^m),\)\(\varphi_j=(y^1,\cdots,y^m)\)とします。\(x^m=y^m=0\)で固定した場合、\(\varphi_i,\varphi_j\)は、\(\partial M\)の局所座標になるので、座標変換を \[y^{j}=y^j(x^1,\cdots,x^{m-1},0),\ (j=1,\cdots,m-1)\] とすれば、座標変換のヤコビアンは、 \[J_{\partial M}=\delta_{\mu_1\cdots\mu_{m-1}}^{1\cdots m-1}\frac{\partial y^1}{\partial x^{\mu_1}}\cdots\frac{\partial y^{m-1}}{\partial x^{\mu_{m-1}}}\] となります。\(\mu_i\)の添え字に関しての総和を省略してます。上半空間同士の座標変換を \[y^{j}=y^j(x^1,\cdots,x^{m-1},0),\ (j=1,\cdots,m-1)\] \[y^m=y^m(x^1,\cdots,x^m)\] とすれば、\(M\)は向き付け可能なので、座標変換のヤコビアンは正にできます。 \[J=\delta_{\mu_1\cdots\mu_{m-1}\mu_{m}}^{1,\cdots,m-1,m}\frac{\partial y^1}{\partial x^{\mu_1}}\cdots\frac{\partial y^{m-1}}{\partial x^{\mu_{m-1}}}\frac{\partial y^m}{\partial x^{\mu_m}}\gt0\] \(\mu_1,\cdots,\mu_{m-1}\)は、\(x^m\)に依らないので、\(\mu_1,\cdots,\mu_{m-1}=m\)となる項はすべて０になり、自動的に\(\mu_m=m\)に決まります。 \[J=\delta_{\mu_1\cdots\mu_{m-1}m}^{1,\cdots,m-1,m}\frac{\partial y^1}{\partial x^{\mu_1}}\cdots\frac{\partial y^{m-1}}{\partial x^{\mu_{m-1}}}\frac{\partial y^m}{\partial x^{m}}\gt0\] δの記号の最後の添え字が、\(m\)番目から、\(m\)番目の置換で無視してよいため、\(\delta_{\mu_1\cdots\mu_{m-1}}^{1\cdots m-1}\)と同じです。また\(x^m,y^m\)軸はどちらも多様体内側が正なので、\(\frac{\partial y^m}{\partial x^{m}}\gt0\)です。 \[J=\underbrace{\delta_{\mu_1\cdots\mu_{m-1}}^{1\cdots m-1}\frac{\partial y^1}{\partial x^{\mu_1}}\cdots\frac{\partial y^{m-1}}{\partial x^{\mu_{m-1}}}}_{=J_{\partial M}}\ \underbrace{\frac{\partial y^m}{\partial x^{m}}}_{\gt0}\gt0\] 以上より、\(M\)の座標の向きを決めると、\(\partial M\)の座標の向きも一致することが分かりました。各チャートで座標の向きを一致させて、 \[\int_{M}d\omega=\sum_{i=1}^k\int_{U_i}\phi_id\omega=\int_{U_i}\sum_{i=1}^k\phi_id\omega\] ここで、1の分割の定義\(\sum\phi_i=1\)、外微分\(d\)の線形性\(\sum d\phi_i=d\sum\phi_i\)また、ライプニッツ則\(d(\sum\phi_i\omega)=d(\sum\phi_i)\omega+\sum\phi_id\omega\)から、 \[\sum_{i=1}^k\phi_id\omega=\sum_{i=1}^k\phi_id\omega+\underbrace{d\left(\sum_{i=1}^k\phi_i\right)}_{=0}\omega\] \[=d\left(\sum_{i=1}^k\phi_i\omega\right)=\sum_{i=1}^kd(\phi_i\omega)\] となり、 \[\int_{M}d\omega=\sum_{i=1}^k\int_{U_i}d(\phi_i\omega)=\sum_{i=1}^k\int_{\partial M\cap U_i}\phi_i\omega=\int_{\partial M}\omega\] 終わりです。