楽しい科学（理論）チャンネル

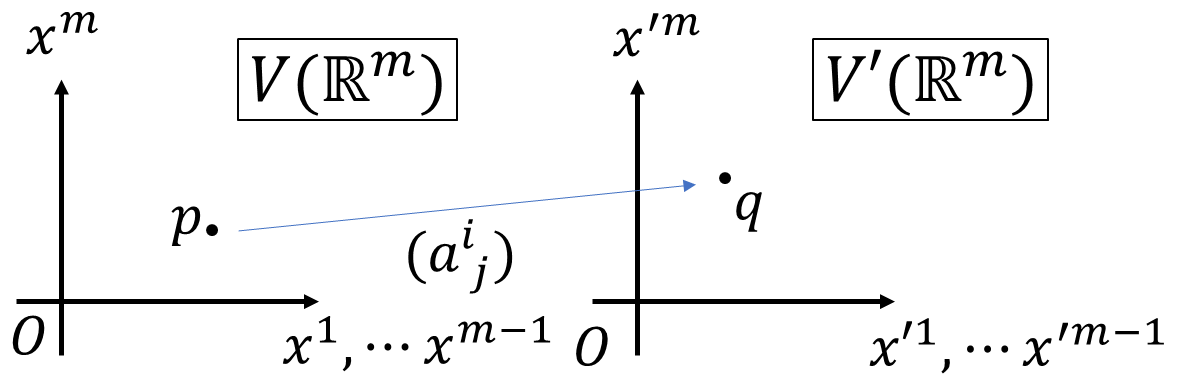
\(a^i_{\ j}\)を\(x'^i,x^j\)を用いて表していきます。仮定より以下のような一次変換が成り立っています。 \[x'^i=a^i_{\ 1}x^1+\cdots+a^i_{\ j}x^j+\cdots+a^i_{\ m}x^m\] この式の両辺を\(x^j\)で偏微分します。 \[\frac{\partial x'^i}{\partial x^j}=a^i_{\ 1}\frac{\partial x^1}{\partial x^j}+\cdots+a^i_{\ j}\frac{\partial x^j}{\partial x^j}+\cdots+a^i_{\ m}\frac{\partial x^m}{\partial x^j}\] \((x^1,\cdots,x^m)\)は独立な成分なので、 \[\frac{\partial x^i}{\partial x^j}=\begin{cases}1,\quad i=j\\ 0,\quad i\neq j\end{cases}\] となります。 \[\frac{\partial x'^i}{\partial x^j}=a^i_{\ 1}\times0+\cdots+a^i_{\ j}\times1+\cdots+a^i_{\ m}\times0=a^{i}_{\ j}\] これで\(a^i_{\ j}\)が求まりました。先ほどの偏微分はよく出てくるので、クロネッカーのデルタ\(\delta^i_{\ j}\)と定義されています。 \[\delta^i_{\ j}:=\frac{\partial x^i}{\partial x^j}=\begin{cases}1,\quad i=j\\ 0,\quad i\neq j\end{cases}\] 同じ計算を総和記号を使ってもう一度やってみます。 \[x'^i=\sum_{k=1}^ma^i_{\ k}x^k\] 両辺を\(x^j\)で偏微分します。 \[\frac{\partial x'^i}{\partial x^j}=\sum_{k=1}^ma^i_{\ k}\frac{\partial x^k}{\partial x^j}=\sum_{k=1}^ma^i_{\ k}\delta^k_{\ j}=a^i_{\ j}\] 最後の等号は、クロネッカーのデルタがあるので、\(k\)に関する総和について\(k\neq j\)の項はすべて０になって、唯一、\(k=j\)となる項だけ残るので、成立します。よってベクトルの成分、基底の座標変換は、 \[X'^i=\sum_{j=1}^m\frac{\partial x'^i}{\partial x^j}X^j,\ e_i=\sum_{j=1}^m\frac{\partial x'^j}{\partial x^i}e'_j\] となります。今まで見てきませんでしたが、 \[X^i=\sum_{j=1}^mb^i_{\ j}X'^j,\ e'_i=\sum_{j=1}^mb^j_{\ i}e_j\] このような逆の変換も表せるでしょうか？この表記法のおかげ逆の変換も簡単に求まります。次は\(V'\)上の点\(q(x'^1,\cdots,x'^m)\)を一次変換\((b^i_{\ j})\)によって\(V\)上の点\(p(x^1,\cdots,x^m)\)に写せたとします。 \[x^i=\sum_{k=1}^mb^i_{\ k}x'^k\] このように先ほどの逆の一次変換を考えます。先ほどと同様に両辺を\(x'^j\)で偏微分して、 \[\frac{\partial x^i}{\partial x'^j}=\sum_{k=1}^mb^i_{\ k}\frac{\partial x'^i}{\partial x'^j}=\sum_{k=1}^mb^i_{\ k}\delta^k_{\ j}=b^i_j\] となります。偏微分を使った記法により \[X^i=\sum_{j=1}^m\frac{\partial x^i}{\partial x'^j}X'^j,\ e'_i=\sum_{j=1}^m\frac{\partial x^j}{\partial x'^i}e_j\] \[X'^i=\sum_{j=1}^m\frac{\partial x'^i}{\partial x^j}X^j,\ e_i=\sum_{j=1}^m\frac{\partial x'^j}{\partial x^i}e'_j\] 基底ベクトルと、成分の行ったり来たりが自由自在になりました。今導いた偏微分を使った一次変換を使ってベクトル\(X\)が座標変換で変化しないことを確かめましょう。 \[X=\sum_{i=1}^mX^ie_i\] \[=\sum_{i=1}^m\left(\sum_{j=1}^m\frac{\partial x^i}{\partial x'^j}X'^j\right)\left(\sum_{k=1}^m\frac{\partial x'^k}{\partial x^i}e'_k\right)\] \[=\sum_{i=1}^m\sum_{j=1}^m\sum_{k=1}^m\frac{\partial x^i}{\partial x'^j}\frac{\partial x'^k}{\partial x^i}X'^je'_k\] 各項に出てくる偏微分の部分を計算してみます。よくよく見ると第１回でやったチェーンルールがありますね。 \[\sum_{i=1}^m\frac{\partial x^i}{\partial x'^j}\frac{\partial x'^k}{\partial x^i}=\frac{\partial x'^k}{\partial x'^j}=\delta^k_{\ j}\] チェーンルールを使ってクロネッカーのデルタが出てきました。これは\(k=j\)なら1それ以外は0となる記号です。\(x'^k,x'^j\)が同じ座標系の成分で独立の値を取るためこのようになります。 \[X=\sum_{j=1}^m\sum_{k=1}^m\delta^k_{\ j}X'^je'_k=\sum_{k=1}^mX'^ke'_k\] 総和記号、偏微分の計算ルールによってで、ベクトルの座標変換で、ベクトルが不変に保たれることが簡単な計算で分かりますね。