楽しい科学（理論）チャンネル

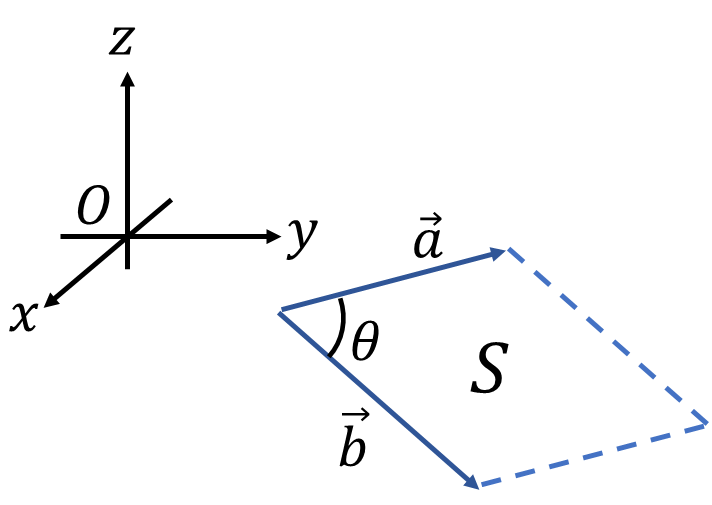
　今回の話は後で置換積分に役に立ちます。初めに、ベクトル\(\vec{a}=(a^1,a^2,a^3),\vec{b}=(b^1,b^2,b^3)\)、この２ベクトルのなす角を\(\theta\)とします。内積の図形的表現を見てみます。余弦定理を使えば簡単です。 \[|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta=|\vec{b}-\vec{a}|^2=(\vec{b}-\vec{a})\cdot(\vec{b}-\vec{a})\] \[|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta=|\vec{b}|^2-2\vec{a}\cdot\vec{b}+|\vec{a}|^2\] \[\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta=\sqrt{\sum_i(a^i)^2}\sqrt{\sum_j(b^j)^2}\cos\theta\] 内積は、２ベクトルの大きさとそのなす角の余弦を掛けた値と等しいってことですね。特に\(|\vec{a}||\vec{b}|\cos\theta=0\)なら\(\theta=\pi/2(0\lt\theta\lt\pi)\)２ベクトルは垂直ということになります。この２つのベクトルこれを利用してベクトル\(\vec{a},\vec{b}\)を隣り合う2辺とする平行四辺形の面積\(S\)を三角比を使わないで求めてみましょう。 \[S=|\vec{a}||\vec{b}|\sin\theta\] \[=\sqrt{\sum_i(a^i)^2}\sqrt{\sum_j(b^j)^2}\sin\theta\] 両辺を2乗します。 \[S^2=\sum_i(a^i)^2\sum_j(b^j)^2(1-\cos^2\theta)\] \[=\sum_i(a^i)^2\sum_j(b^j)^2\left(1-\frac{(a^1b^1+a^2b^2+a^3b^3)^2}{\sum_i(a^i)^2\sum_j(b^j)^2}\right)\] \[=\sum_i\sum_j(a^ib^j)-(a^1b^1)^2-(a^2b^2)^2-(a^3b^3)^2\] \[-2(a^1b^1a^2b^2+a^2b^2a^3b^3+a^3b^3a^1b^1)\] \[=(a^1b^2)^2-2a^1b^1a^2b^2+(a^2b^1)^2\] \[+(a^2b^3)^2-2a^2b^2a^3b^3+(a^3b^2)^2\] \[+(a^3b^1)^2-2a^3b^3a^1b^1+(a^1b^3)^2\] 以上から、 \[S^2=(a^1b^2-a^2b^1)^2+(a^2b^3-a^3b^2)^2+(a^3b^1-a^1b^3)^2\] \(S\gt0\)なのでこれの平方根が平行四辺形の面積となります。一瞬だけ2次元の話をします。2次元のベクトル\(\vec{a},\vec{b}\)について3次元のベクトルの\(z\)成分だけを０としたものとすれば、\(x,y\)平面でベクトル\(\vec{a},\vec{b}\)が作る平行四辺形の面積は上の式から\(a^3=b^3=0\)として \[S_{xy}=|a^1b^2-a^2b^1|\] となります。\(|a|\)は\(a\)の絶対値でもし\(a\)が負だったらプラスにします。3次元に話を戻してベクトル\(\vec{S}\)を、 \[\vec{S}=\begin{pmatrix}a^2b^3-a^3b^2 \\a^3b^1-a^1b^3 \\a^1b^2-a^2b^1\end{pmatrix}\] というベクトルとみなしてみます。面積は、\(S=\sqrt{\vec{S}\cdot\vec{S}}\)となります。 \[\vec{S}\cdot\vec{a}=a^1a^2b^3-a^1b^2a^3+b^1a^2a^3-a^1a^2b^3\] \[a^1b^2a^3-b^1a^2a^3=0\] \[\vec{S}\cdot\vec{b}=b^1a^2b^3-b^1b^2a^3+b^1b^2a^3-a^1b^2b^3\] \[a^1b^2b^3-b^1a^2b^3=0\] つまり\(\vec{S}\)は平行四辺形に垂直なベクトルとなります。更に平行六面体の体積を求めてみます。

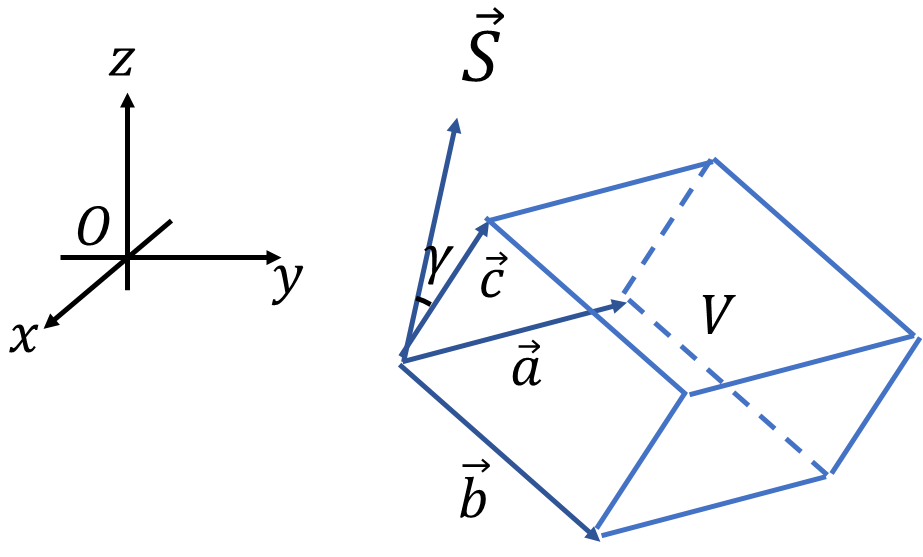
　ベクトル\(\vec{a},\vec{b},\vec{c}\)を隣り合う３辺とする平行6面体(平行四辺形が６面の図形)の体積\(V\)を求めてみましょう。先ほど求めた\(|\vec{S}|\)を底辺として、高さ\(h\)を求めてみます。また底辺垂直からの\(\vec{c}\)の角度を\(\gamma\)とします。底辺に垂直なベクトル\(\vec{S}\)を利用して、 \[h=|\vec{c}|\cos\gamma=|\vec{c}|\left|\frac{\vec{S}}{|\vec{S}|}\right|\cos\gamma\] 単位法線ベクトル\(|\vec{S}/|\vec{S}||\)を勝手にかけてますが、\(|\vec{S}/|\vec{S}||=|\vec{S}|/|\vec{S}|=1\)なので問題ないです。これにより高さ\(h\)はベクトル\(c\)と法線単位ベクトルの内積であることが分かります。 \[h=\vec{c}\cdot\left(\frac{1}{|\vec{S}|}\vec{S}\right)=\frac{1}{|\vec{S}|}\vec{c}\cdot\vec{S}\] ベクトル\(\vec{c}\)と法線単位ベクトルの内積で求まります。よって体積\(V\)は \[V=h|\vec{S}|=\vec{S}\cdot\vec{c}\] \[=\begin{pmatrix}a^2b^3-a^3b^2 \\a^3b^1-a^1b^3 \\a^1b^2-a^2b^1\end{pmatrix}\begin{pmatrix}c_1\\c_2\\c_3\end{pmatrix}\] \[V=a^1b^2c^3-a^2b^1c^3+a^3b^1c^2\] \[-a^1b^3c^2+a^2b^3c^1-a^3b^2c^1\] となります。

くさび積という計算ルールを決めてその有用性を見ていきます。基底ベクトルについてくさび積\(\wedge\)は \[e_1\wedge e_2=-e_2\wedge e_1\] 積の順番を変えると符号が変わるものとします。基底ベクトルが2個掛けられているものを２ベクトルと呼びます。次の式は基底が４個掛けられているので４ベクトルです。 \[\begin{align}e_j\wedge e_1\wedge e_2\wedge e_3&=-e_1\wedge e_j\wedge e_2\wedge e_3 \\&=(-1)^2e_1\wedge e_2\wedge e_j\wedge e_3 \\&=(-1)^3e_1\wedge e_2\wedge e_3\wedge e_j\end{align}\] 基底\(e_j\)を3個飛ばして移動させた４ベクトルを\((-1)^3\)倍するともとの４ベクトルと等しいというわけです。一般に\(k\)ベクトルのある基底が\(n\)個の基底を飛ばして移動することによって得られた\(k\)ベクトルは\((-1)^n\)倍すると元の\(k\)ベクトルと等しくなります。またスカラー\(a,b\)について \[(ae_1)\wedge (be_2)=abe_1\wedge e_2\] \[ae_1\wedge e_2+be_1\wedge e_2=(a+b)e_1\wedge e_2\] \[e_1\wedge(e_2+e_3)=e_1\wedge e_2+e_1\wedge e_3\] このようにくさび積の順番に注意すれば実数の文字式のように計算できるものとします。スカラーはくさび積の途中に書いてもいいですし、左に持ってきてもいいことにします。特に\(e_1\wedge e_1=0\)となります。これは簡単に示すことができます。積の順番を入れ替えて \[e_1\wedge e_1=-e_1\wedge e_1\] 左辺に移項して \[2e_1\wedge e_1=0\] \[e_1\wedge e_1=0\] 同じ基底ベクトルのくさび積は０になります。５ベクトルとかでも同じ基底が含まれていれば0になります。 \[\begin{align}\mathop{e_1\wedge e_2\wedge e_3\wedge e_4\wedge e_2}_{5ベクトル}&=(-1)^{1} e_2\wedge e_1\wedge e_3\wedge e_4\wedge e_2 \\&=(-1)^{1+3}\underbrace{e_2\wedge e_2}_{=0}\wedge e_1\wedge e_3\wedge e_4 \\&=0\end{align}\] \(n\)ベクトルの２つの基底の位置を入れ替えると符号が変わります。間に何個の基底が挟まっていても関係ないです。順番に見ていきましょう。 \[\mathop{e_1\wedge\cdots\wedge e_i\wedge e_j\wedge\cdots\wedge e_n}_{隣り合う基底の交換}=-e_1\wedge\cdots\wedge e_j\wedge e_i\wedge\cdots\wedge e_n\] \[\begin{align}&\mathop{e_1\wedge\cdots\wedge e_i\wedge e_\alpha\wedge e_j\wedge\cdots\wedge e_n}_{1個飛ばしの基底の交換} \\=&(-1)^1e_1\wedge\cdots\wedge e_\alpha\wedge e_i\wedge e_j\wedge\cdots\wedge e_n \\=&(-1)^{(1+1)}e_1\wedge\cdots\wedge e_\alpha\wedge e_j\wedge e_i\wedge\cdots\wedge e_n \\=&(-1)^{(1+1+1)}e_1\wedge\cdots\wedge e_j\wedge e_\alpha\wedge e_i\wedge\cdots\wedge e_n \\=&-e_1\wedge\cdots\wedge e_j\wedge e_\alpha\wedge e_i\wedge\cdots\wedge e_n\end{align}\] \[\begin{align}&\mathop{e_1\wedge\cdots\wedge e_i\wedge e_\alpha\wedge e_\beta\wedge e_j\wedge\cdots\wedge e_n}_{2個飛ばしの基底の交換} \\=&(-1)^2e_1\wedge\cdots\wedge e_\alpha\wedge e_\beta\wedge e_i\wedge e_j\wedge\cdots\wedge e_n \\=&(-1)^{(2+1)}e_1\wedge\cdots\wedge e_\alpha\wedge e_\beta\wedge e_j\wedge e_i\wedge\cdots\wedge e_n \\=&(-1)^{(2+1+2)}e_1\wedge\cdots\wedge e_j\wedge e_\alpha\wedge e_\beta\wedge e_i\wedge\cdots\wedge e_n \\=&-e_1\wedge\cdots\wedge e_j\wedge e_\alpha\wedge e_\beta\wedge e_i\wedge\cdots\wedge e_n\end{align}\] ここまで見れば分かると思いますが、任意の２つの基底\(e_i,e_j\)のを交換する場合 \[\begin{align}&e_1\wedge\cdots\wedge e_i\wedge \underbrace{\cdots}_{m個}\wedge e_j\wedge\cdots\wedge e_n \\=&(-1)^me_1\wedge\cdots\wedge \underbrace{\cdots}_{m個}\wedge e_i\wedge e_j\wedge\cdots\wedge e_n \\=&(-1)^{(m+1)}e_1\wedge\cdots\wedge \underbrace{\cdots}_{m個}\wedge e_j\wedge e_i\wedge\cdots\wedge e_n \\=&(-1)^{(2m+1)}e_1\wedge\cdots\wedge e_j\wedge \underbrace{\cdots}_{m個}\wedge e_i\wedge\cdots\wedge e_n \\=&-e_1\wedge\cdots\wedge e_j\wedge \underbrace{\cdots}_{m個}\wedge e_i\wedge\cdots\wedge e_n\end{align}\] 　こうなります。 \(n\)ベクトルの任意の基底\(e_i,e_j\)について、間にある基底の数にかかわらず、\(e_i,e_j\)を入れ替えると\(n\)ベクトルの符号が変わります。 これを交代性といいます。

\(k\)個のベクトルのくさび積も\(k\)ベクトルになります。\(k\)ベクトルと空間の次元について見ていきます。まずは１から３次元まで 3次元空間の２ベクトルのくさび積だけ特別扱い(ホッジ作用素)しましたが、くさび積の導入で、ベクトルの積とベクトルが作る立体の体積(面積)と対応が付くようになりました。