楽しい科学（理論）チャンネル

　初めに簡単なリーマン積分を見ていきます。数直線\(\mathbb{R}\)上区間\((a,b)\)とあまり変な形をしていない関数\(f:\mathbb{R}\to\mathbb{R}\)について、 \[a=x_0\lt x_1\lt\cdots\lt x_n=b\] このように区間を分割して、変化量を \[\varDelta x_i:=x_{i}-x_{i-1}\] このように定義します。関数\(f:\mathbb{R}\to\mathbb{R}\)の積分を \[\int_{(a,b)}fdx:=\lim_{n\to\infty}\sum_{i=1}^nf_i\varDelta x_i\] このように定義します。ただし、\(f_i\)は、\((x_i,x_{i-1})\)の間の\(f\)の値です。積分とは底辺\(\varDelta x_i\)、高さ\(f_i\)の細長い長方形を足し合わせたものです。ちなみに \[\int_{(a,b)}fdx:=\int_{[a,b]}fdx=\int_a^bfdx\] 積分の値は開区間、閉区間に依らず同じ値を取ります。リーマン積分風にいうと、底辺が点\(a\)、高さ\(f(a)\)の長方形の面積は０なので、閉区間にしても面積は変わりません。

　なめらかで単調増加な写像\(\varphi:t\mapsto x\)について、\(\mathbb{R}\)上の区間\((\varphi^{-1}(a),\varphi^{-1}(b))\)を \[\varphi^{-1}(a)=t_0\lt t_1\lt\cdots\lt t_n=\varphi^{-1}(b)\] と分割します。変化量を\(\varDelta t_i=t_i-t_{i-1}\)とすれば、 \[\int_a^bfdx=\lim_{n\to\infty}\sum_{i=1}^nf_i\varDelta x_i=\lim_{n\to\infty}\sum_{i=1}^nf_i\frac{\varDelta x_i}{\varDelta t_i}\varDelta t_i\] \(x\)を\(t\)の関数\(\varphi(t)\)とみなせば、\(\frac{\varDelta x_i}{\varDelta t_i}\)の極限\(n\to\infty\)は微分なので、\(f\)と微分を１つの\(t\)の関数とみなします。 \[f\frac{dx}{dt}:t\mapsto f(t)\frac{dx}{dt}(t)\] 以上から、 \[\int_a^bfdx=\lim_{n\to\infty}\sum_{i=1}^nf_i\frac{\varDelta x_i}{\varDelta t_i}\varDelta t_i=\int_{\varphi^{-1}(a)}^{\varphi^{-1}(b)}f\frac{dx}{dt}dt\] 置換積分の公式が得られます。

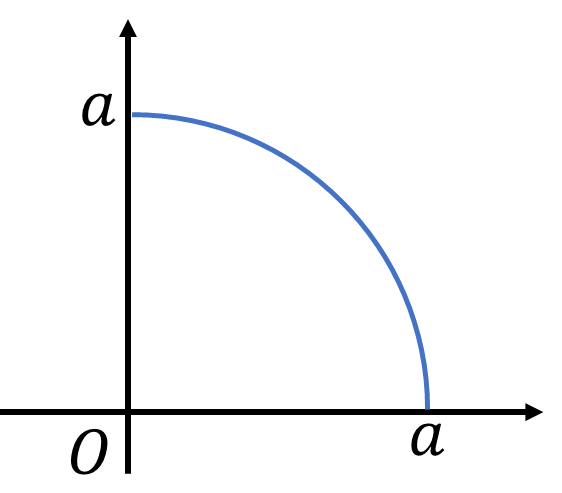
　置換積分の例として円の面積\(S\)を求めてみます。区間\([0,a]\)で関数\(4\sqrt{a^2-x^2}\)を積分すればいいので、 \[S=\int_0^a4\sqrt{a^2-x^2}dx\] このままでは計算できないので、\(x=a\sin t\)と変換してみましょう。逆写像\(t=\sin^{-1}x/a\)を使いたいので第1象限だけの積分を４倍することにしています。置換積分をして \[\begin{align}S&=\int_{\sin^{-1}0/a}^{\sin^{-1}a/a}4\sqrt{a^2-a^2\sin^2t}\frac{dx}{dt}dt \\&=\int_0^{\pi/2}4a\cos t\times a\cos tdt \\&=4a^2\int_0^{\pi/2}\cos^2 tdt\end{align}\] どのように解いてもいいですが今回はオイラーの公式\(\cos t=(e^{it}+e^{-it})/2\)を使います。\(i\)は虚数単位\(\sqrt{-1}\)です。 \[\begin{align}S&=a^2\int_0^{\pi/2}(e^{2it}+2+e^{-2it})dt \\&=a^2\left[\frac{e^{2it}-e^{-2it}}{2i}+2t\right]_0^{\pi/2} \\&=\pi a^2\end{align}\] 虚数部分はうまいこと消えてくれました。

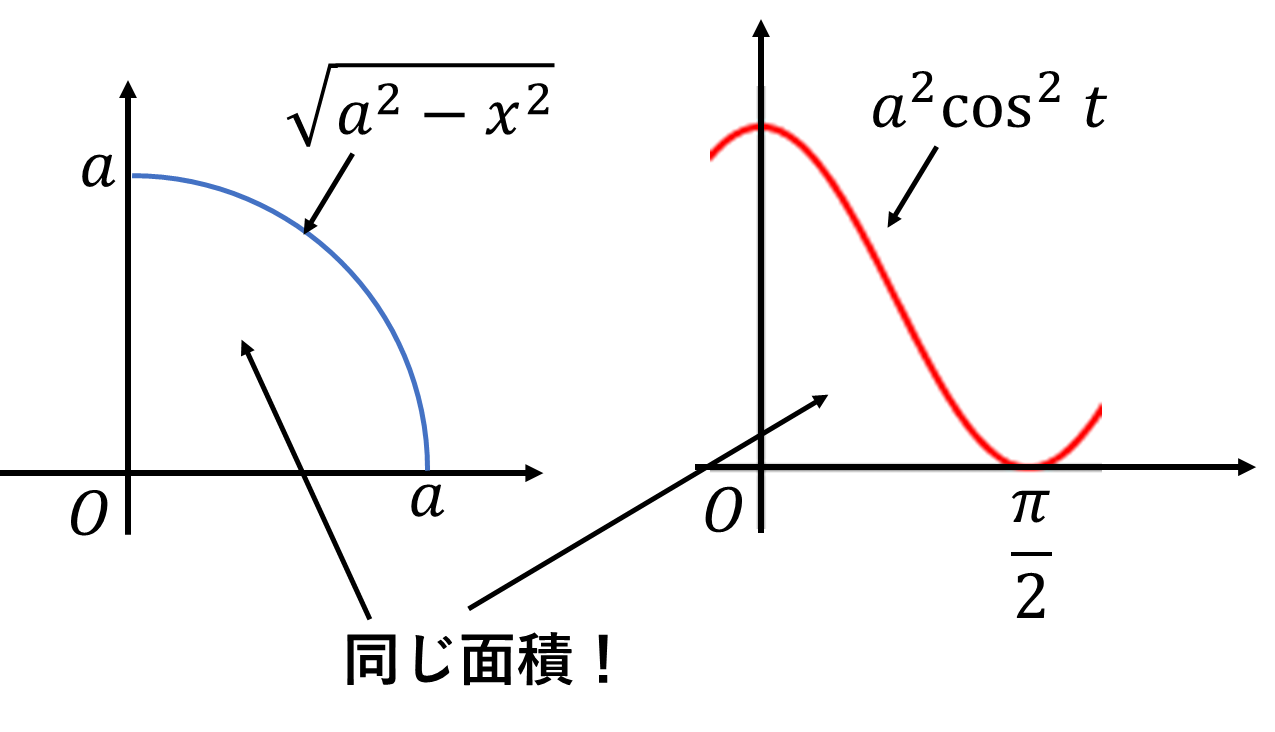
別の数直線\(\mathbb{R}\ni x,\ \mathbb{R}'\ni t\)上の積分ともとらえられますが、

リーマン和をなす長方形の底辺を\(\varDelta x_i\)から、\(a\cos t_j\varDelta t_j\)に変えたという見方もできます。 \[\lim_{n\to\infty}\sum_{i=1}^nf_i\varDelta x_i=\lim_{m\to\infty}\sum_{j=1}^mf_j\frac{dx_j}{dt_j}\varDelta t_j\] 置換積分の公式が成立しているイメージがしっくりくるかもしれません。長さ\(a\)の線分を\(L\)と表し、\(x\)の座標では、\((0,a)\)区間を表し、\(t\)の座標では、\((0,\pi/2)\)の区間を表すと約束すれば、 \[\int_Lfdx=\int_Lf\frac{dx}{dt}dt\] と表せることにしましょう。のちに引き戻しという概念を扱うことでより厳密に表記できます。線分\(L\)は同じ\(\mathbb{R}\)上にありますが、リーマン和の底面部分の取り方に違いがあるということです。極限を取れば、あまり変な分割をしなければどのように底面をとっても同じ積分値に収束するはずです。重積分の座標変換ではこのイメージを持って、\(\mathbb{R}^2\)上の図形\(M\)底面の分割方法を変えるという操作を考えます。

　2次元ユークリッド空間上関数\(f:\mathbb{R}^2\to\mathbb{R}\)とあまり複雑な形をしていない領域\(M\)について、重積分を \[\int_Mfdx^1dx^2:=\int_a^b\int_{g_{-}}^{g_+}fdx^1dx^2\] と定義します。ただし、\(a,b\)は領域\(M\)の\(x^1\)軸への射影のうち一番小さい値を\(a\)、一番大きい値を\(b\)とします。領域\(M\)の境界\(\partial M\)を点\(a,b\)で切ったときできる２つの曲線のうち上側を\(x^2=g_+(x^1)\)、下側を\(x^2=g_{-}(x^1)\)と表しています。

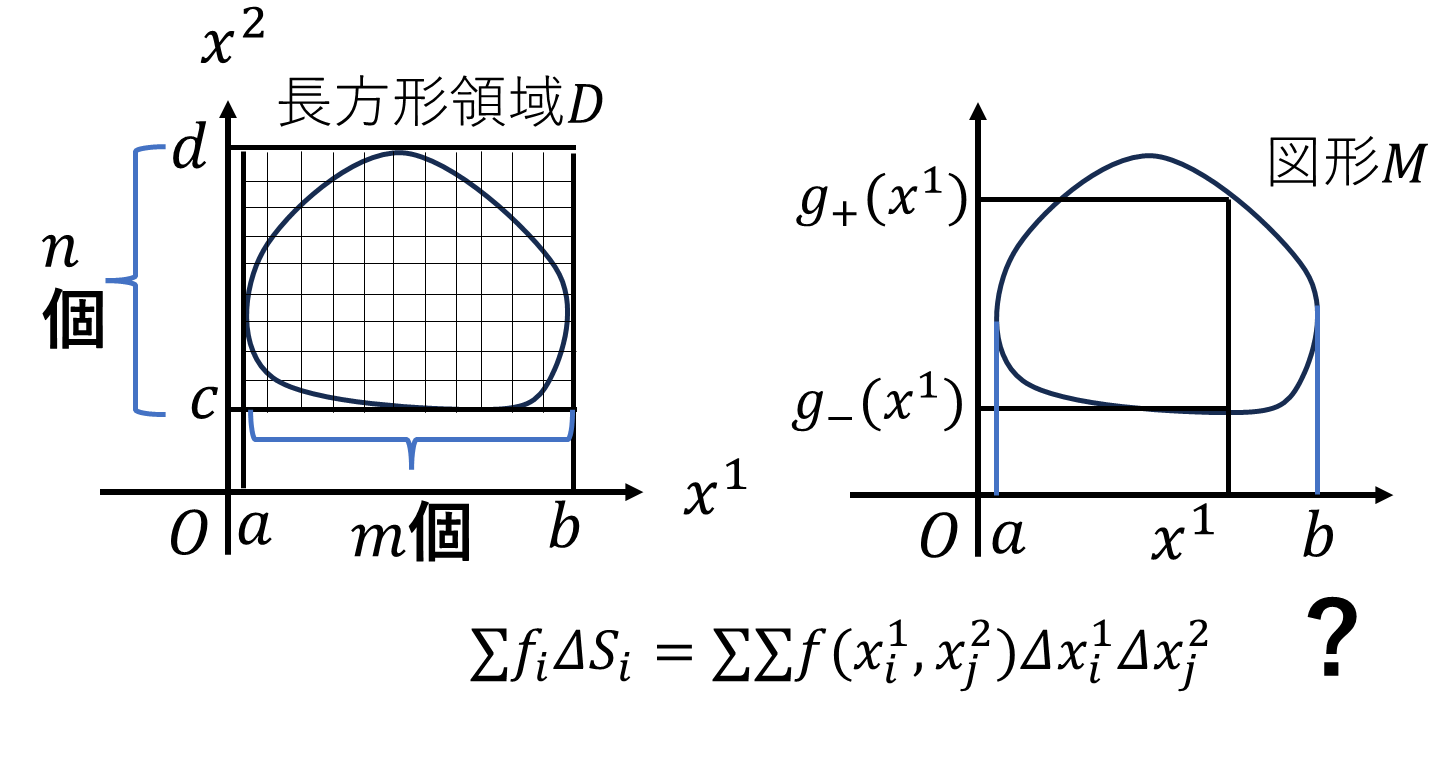
　領域\(M\)を小さい長方形\(\varDelta x^1_i\varDelta x^2_j\)で分割して、小さい長方形内での\(f\)の値を\(f_{ij}\)とすれば、 \[\int_{M}fdx^1dx^2=\lim_{m,n\to\infty}\sum_{(x^1_i,x^2_j)\in M}f_{ij}\varDelta x^1_i\varDelta x^2_j\] でも重積分を表すことができます。今の総和記号では計算がしずらいので、新たに関数\(\lambda:\mathbb{R}^2\to\mathbb{R}\)を \[\lambda:=\begin{cases}1&,(x^1,x^2)\in M\\ 0&,(x^1,x^2)\notin M\end{cases}\] 定義します。\(M\)の内側で１、外で０という単純な関数ですが、 \[\int_{M}fdx^1dx^2=\int_D\lambda fdx^1dx^2\] 重積分を、\(M\)を包含する長方形領域\(D\supset M\)の積分に変えることができます。\(M\cap D\)の部分では、\(\lambda=0\)となりますので、\(M\)上のみでの積分値だけ寄与するということですね。領域\(M\)の境界を表すグラフを使う定義と、リーマン和っぽい定義、重積分の定義を２つ与えてしまいましたが、 \[D=\left\{(x^1,x^2)\ \middle|\ a\le x^1\le b,\ c\le x^2\le d\right\}\] とすれば、 \[\int_{M}fdx^1dx^2:=\lim_{m,n\to\infty}\sum_{(x^1_i,x^2_j)\in M}f_{ij}\varDelta x^1_i\varDelta x^2_j\] これを関数\(\lambda\)領域\(D\)のリーマン和に変えます。 \[=\lim_{m,n\to\infty}\sum_{i=1}^m\sum_{j=1}^n\lambda_{ij} f_{ij}\varDelta x^1_i\varDelta x^2_j\] \[=\lim_{m\to\infty}\sum_{i=1}^m\left(\lim_{n\to\infty}\sum_{j=1}^n\lambda_{ij} f_{ij}\varDelta x^2_j\right)\varDelta x^1_i\] カッコの中身だけ積分に変えます。本当は極限、総和の順番で計算結果が変わらないか調べる必要があります。 \[=\lim_{m\to\infty}\sum_{i=1}^m\left(\int_c^d\lambda fdx^2\right)\varDelta x^1_i\] カッコの中の積分は、\(\lambda\)の性質から、\(x^2\in(g_-,g_+)\)の範囲以外で積分値は０となるので、 \[\lim_{m,n\to\infty}\sum_{(x^1_i,x^2_j)\in M}f_{ij}\varDelta x^1_i\varDelta x^2_j=\lim_{m\to\infty}\sum_{i=1}^m\left(\int_{g_-(x^1)}^{g_+(x^1)} fdx^2\right)\varDelta x^1_i\] \[=\int_a^b\left(\int_{g_-(x^1)}^{g_+(x^1)} fdx^2\right)dx^1=\int_a^b\int_{g_-(x^1)}^{g_+(x^1)}fdx^1dx^2\] ２つの定義は同値です。

　重積分でも置換積分みたいなものを考えたいです。リーマン和の底面となる図形の取り方を変えることで重積分の座標変換を行います。

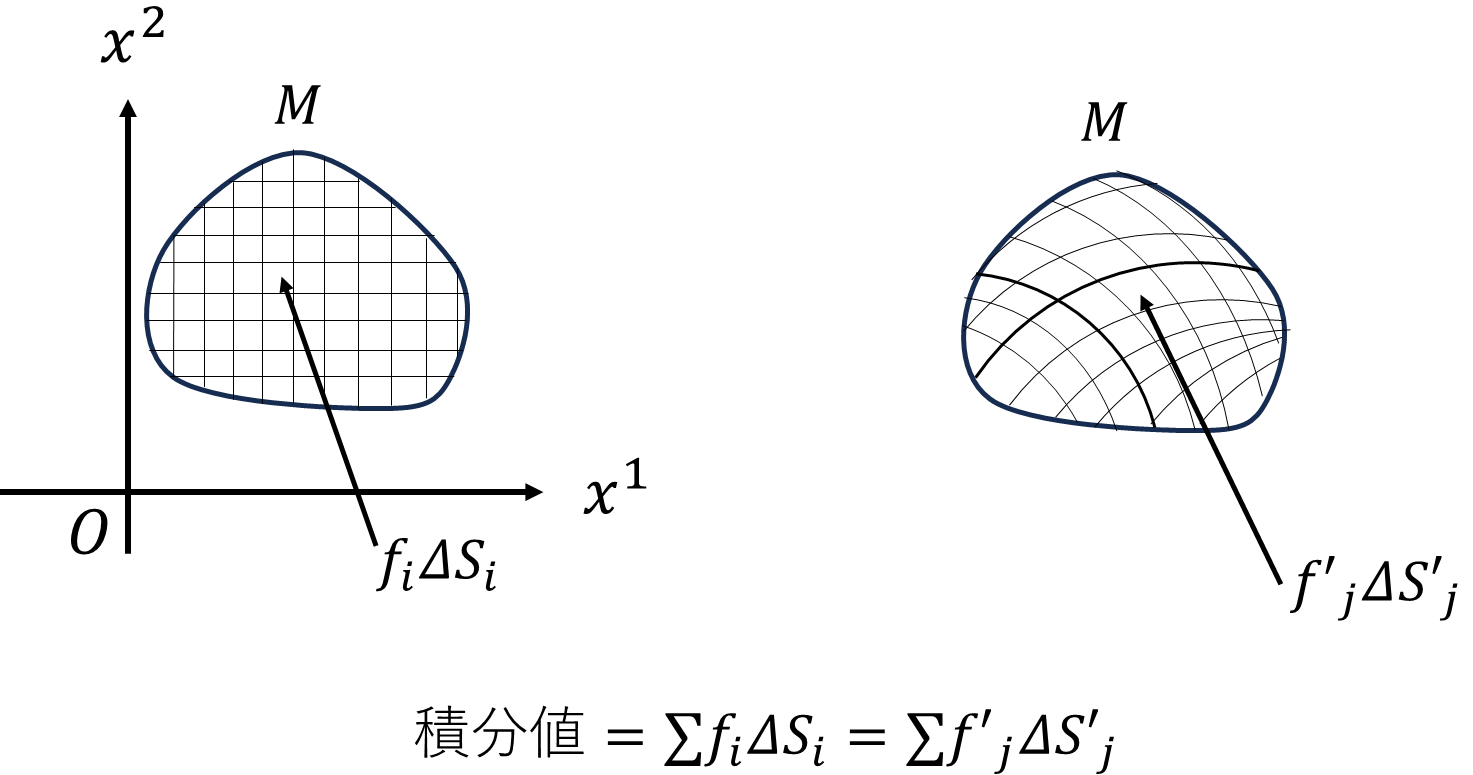
さっきまで、\(\varDelta x^1,\varDelta x^2\)が垂直に交わるとしていましたが、 \(y^1,y^2\)を指定すると、２次元ユークリッド空間上\(\mathbb{R}^2\)の点\(p\)を１つ指定できて、\(\mathbb{R}^2\)上の点\(p\)に対応する、\(y^1,y^2\)が１つに定まる。 関数 \[\varphi^1:(y^1,y^2)\mapsto x^1(y^1,y^2)\] \[\varphi^2:(y^1,y^2)\mapsto x^2(y^1,y^2)\] が微分可能である。

　この２つを満たす新たな座標\((y^1,y^2)\)を取ります。座標変換全体を \[\varphi:(y^1,y^2)\mapsto(x^1,x^2)\] と表すことにします。

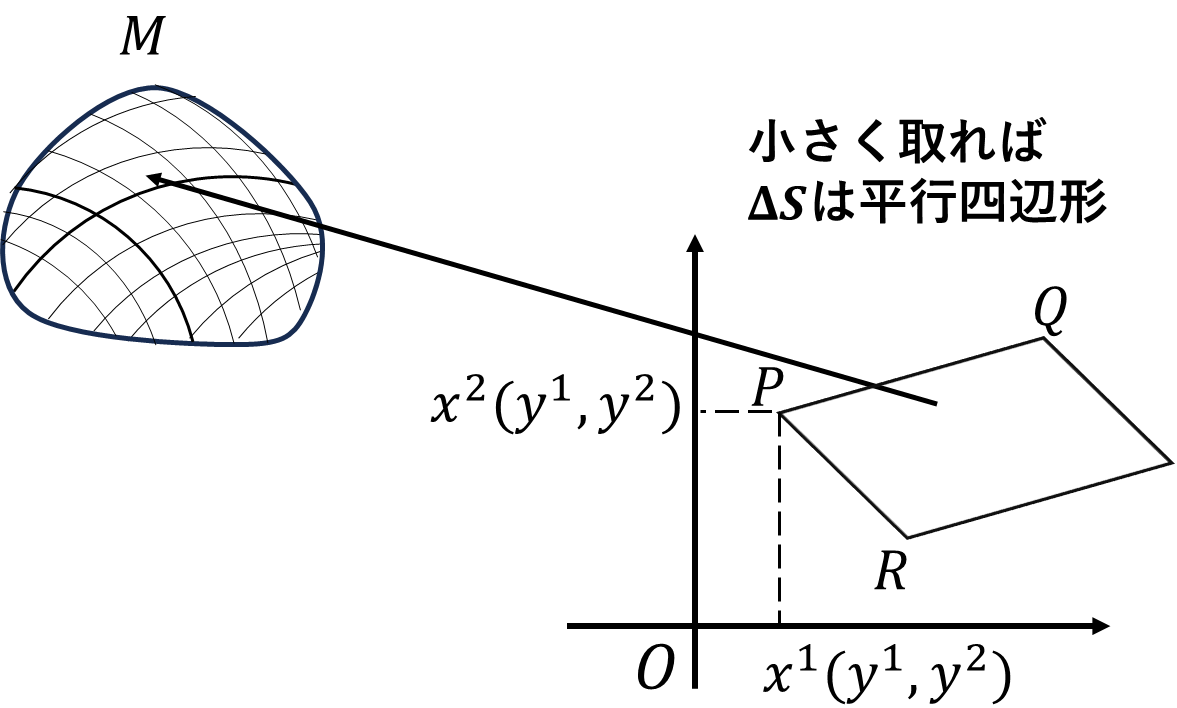
　\(y^1,y^2\)それぞれの変化量を\(\varDelta y^1,\varDelta y^2\)とします。点 \[P(x^1(y^1,y^2),x^2(y^1,y^2))\] を\(\varDelta y^1\)ずらした点を\(Q\)、\(\varDelta y^2\)ずらした点を\(R\)とします。それぞれの点の位置ベクトルは、 \[\begin{align}\overrightarrow{OP}=&x^1(y^1,y^2)e_1+x^2(y^1,y^2)e_2 \\\overrightarrow{OR}=&x^1(y^1+\varDelta y^1,y^2)e_1+x^2(y^1+ \varDelta y^1,y^2)e_2 \\\overrightarrow{OQ}=&x^1(y^1,y^2+\varDelta y^2)e_1+x^2(y^1,y^2+\varDelta y^2)e_2\end{align}\] と表せます。ただし\(e_1,e_2\)は\(x^1,x^2\)の直交座標の標準基底です。 \[\begin{align}\overrightarrow{PR}=&\overrightarrow{OR}-\overrightarrow{OP} \\=&\frac{x^1(y^1+\varDelta y^1,y^2)-x^1(y^1,y^2)}{\varDelta y^1}\varDelta y^1e_1 \\+&\frac{x^2(y^1+\varDelta y^1,y^2)-x^2(y^1,y^2)}{\varDelta y^1}\varDelta y^1e_2\end{align}\] \(\varDelta y^1\)を十分に小さく取れば偏微分で表せます。 \[\overrightarrow{PR}=\frac{\partial x^1}{\partial y^1}\varDelta y^1e_1+\frac{\partial x^2}{\partial y^1}\varDelta y^1e_2\] 同様にして\(\overrightarrow{PQ}\)も求めます。 \[\overrightarrow{PQ}=\frac{\partial x^1}{\partial y^2}\varDelta y^2e_1+\frac{\partial x^2}{\partial y^2}\varDelta y^2e_2\] この２つのベクトルが作る平行四辺形の面積は、 \[\left(\frac{\partial x^1}{\partial y^1}\frac{\partial x^2}{\partial y^2}-\frac{\partial x^2}{\partial y^1}\frac{\partial x^1}{\partial y^2}\right)\varDelta y^1\varDelta y^2\] 偏微分の部分をヤコビアンと呼びます。 \[\frac{\partial (x^1,x^2)}{\partial (y^1,y^2)}=\frac{\partial x^1}{\partial y^1}\frac{\partial x^2}{\partial y^2}-\frac{\partial x^2}{\partial y^1}\frac{\partial x^1}{\partial y^2}\] ヤコビアンには特別な表記がありますが、単に\(J\)と書くことも多いです。これにより重積分を表すリーマン和を、 \[\sum_{(y^1_i,y^2_j)\in M}f_{ij}\varDelta x^1_{i}\varDelta x^2_j\simeq\sum_{(y^1_k,y^2_l)\in M}f_{kl}J_{kl}\varDelta y^1_{k}\varDelta y^2_l\] \(M\)は座標\((x^1,x^2)\)や、\((y^1,y^2)\)を用いた積分範囲ではなく、積分を行う図形なので、 \[\int_Mfdx^1dx^2=\int_MfJdy^1dy^2\] と書くこともできます。実際に積分をする際は、図形\(M\)が、座標\((x^1,x^2)\)や、\((y^1,y^2)\)でどのように表せるか注意が必要です。

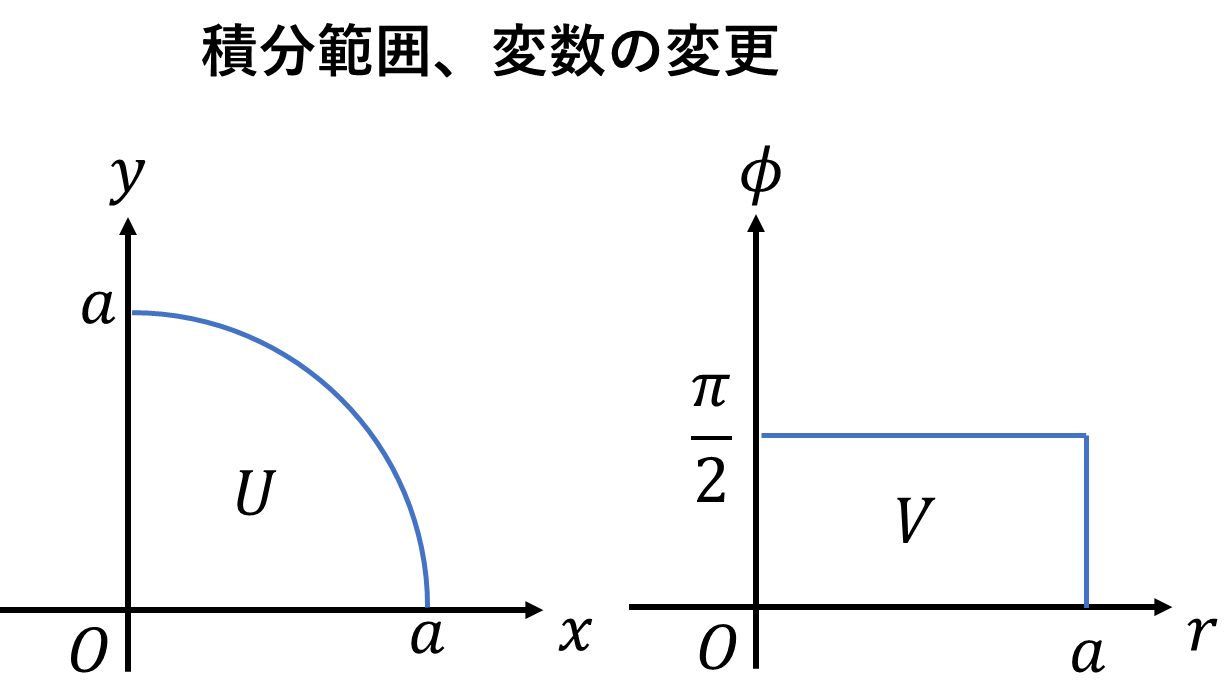
　さっきと全く同じ問題(半径\(a\)の円の面積)を重積分を使って解いていきます。 \[S=\begin{align}\int_0^a4\sqrt{a^2-x^2}dx=&\int_0^a\int_0^{\sqrt{a^2-x^2}}4dydx \end{align}\] ここで\(x,y\)平面上の集合\(U\)を \[U=\left\{(x,y)\middle|0\le x,\ 0\le y,\ \sqrt{x^2+y^2}\le a\right\}\] とします。\(S\)は積分範囲\(U\)、\(f=4\)という関数の面積分となります。 \[S=\iint_U4dxdy\] 極座標\((x,y)=(r\cos\phi,r\sin\phi)\)を取れば、積分範囲は、 \[V=\left\{(r,\phi)\middle| 0\le r\le a,\ 0\le\phi\le\frac{\pi}{2}\right\}\] となります。積分を座標変換をするにはヤコビアンが必要です。計算しておきましょう。 \[J=\frac{\partial x}{\partial r}\frac{\partial y}{\partial \phi}-\frac{\partial y}{\partial r}\frac{\partial x}{\partial \phi}\] \[=\cos\phi\ r\cos\phi+\sin\phi\ r\sin\phi=r\] 極座標を用いて積分はこのように計算できます。 \[\begin{align}\iint_V4rdrd\phi=&4\int_0^{\pi/2}\int_0^ardrd\phi \\=&4\times\frac{a^2}{2}\times\frac{\pi}{2} \\=&\pi a^2\end{align}\]

極座標を取ることで、積分範囲を長方形領域にすることができて、重積分の順序を気にせず楽に積分できました。しかし、重積分の記号 \[\iint_Ufdxdy\] に出てくる\(dxdy\)は微小量\(dx,dy\)の積と考えていいのでしょうか、\(x,y\)の全微分は \[\begin{align}dx=&\frac{\partial r\cos\phi}{\partial r}dr+\frac{\partial r\cos\phi}{\partial \phi}d\phi \\=&\cos\phi\ dr-r\sin\phi\ d\phi \\ \\dy=&\frac{\partial r\sin\phi}{\partial r}dr+\frac{\partial r\sin\phi}{\partial \phi}d\phi \\=&\sin\phi\ dr+r\cos\phi\ d\phi\end{align}\] ですので単に\(dx,dy\)の積は、 \[\begin{align}dxdy=&\cos\phi\sin\phi\ dr^2-r\sin^2\phi\ d\phi dr \\+&\cos^2\phi\ drd\phi+r^2\cos\phi\sin\phi\ d\phi^2\end{align}\] 微小量の積\(dxdy\)と重積分に出てくる\(dxdy\)は別物と考えられます。のちに説明する微分形式は、この部分もうまく整合性が取れています。

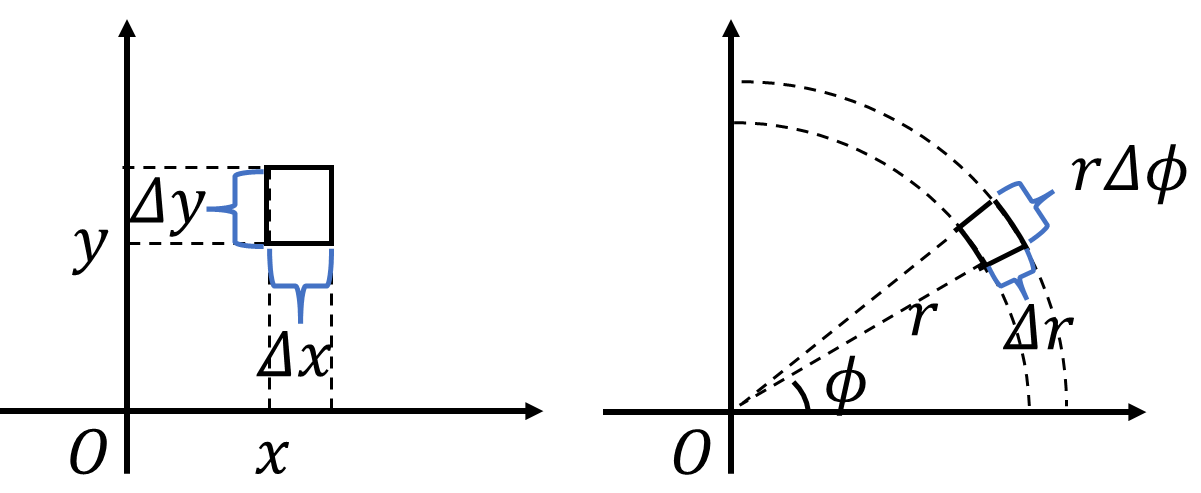
図形\(M\)上の積分を直交座標で表した場合、極座標に変換するヤコビアンは、 \[\begin{align}\frac{\partial (x,y)}{\partial (r,\phi)}=&\frac{\partial x}{\partial r}\frac{\partial y}{\partial \phi}-\frac{\partial x}{\partial \phi}\frac{\partial y}{\partial r} \\=&\cos\phi\times r\cos\phi-(-r\sin\phi)\sin\phi \\=&r\end{align}\] です。\(f=4\)の積分について、 \[\lim_{n\to\infty}\sum_{i=1}^nf_i\underbrace{\varDelta S_i}_{=\varDelta x\varDelta y}=\pi a^2\] \[\lim_{m\to\infty}\sum_{i=1}^mf_j\underbrace{\varDelta S'_j}_{=r\varDelta r\varDelta \phi}=\pi a^2\] ただの積分同様に重積分でも面積要素を作るときの分割の仕方の違いと考えることができます。\(r\)が中心にいくにつれて０に近づくので、ヤコビアンを面積要素の拡大率みたいにとらえることもできます。