3次元での線積分
3次元でも線積分を考えることができます。3次元のベクトル場を\(\vec{f}=(f^x,f^y,f^z)\)とします。2次元の時と同じように\(f_x,f_y,f_z\in\mathbb{R}\)は\(x,y,z\)を変数とするスカラー値関数で、ある曲線\(C\)をパラメータ\(t\in[a,b]\)を使って、表すことができれば、
\[\begin{align}\int_C(f^xdx+f^ydy+f^zdz):=&\lim_{n\to\infty}\sum_{i=1}^n\vec{f}_i\cdot\varDelta\vec{x}_i
\\\int_C\left(f_x\frac{dx}{dt}+f_y\frac{dy}{dt}+f_z\frac{dz}{dt}\right)dt:=&\lim_{m\to\infty}\sum_{j=1}^m\vec{f}_j\cdot\frac{\varDelta\vec{x}(t_j)}{\varDelta t_j}\varDelta t_j\end{align}\]
同じ手順で2次元から3次元に拡張できます。ここにでてくる線素ベクトル\(\varDelta\vec{x}\)は、\(\varDelta\vec{x}=(\varDelta x,\varDelta y,\varDelta z)\)とします。
面積分
3次元での積分には面積分というものもあります。3次元空間の曲面\(S\)上での積分のことです。曲面\(S\)を平行四辺形を使って分割を作ると隙間ができてしまいますが、十分に分割を小さくしていけば、隙間が小さくなっていきます。(ただし分割を増やせば隙間の数が多くなってしまうので、そこはちゃんと評価する必要があると思いますが、)
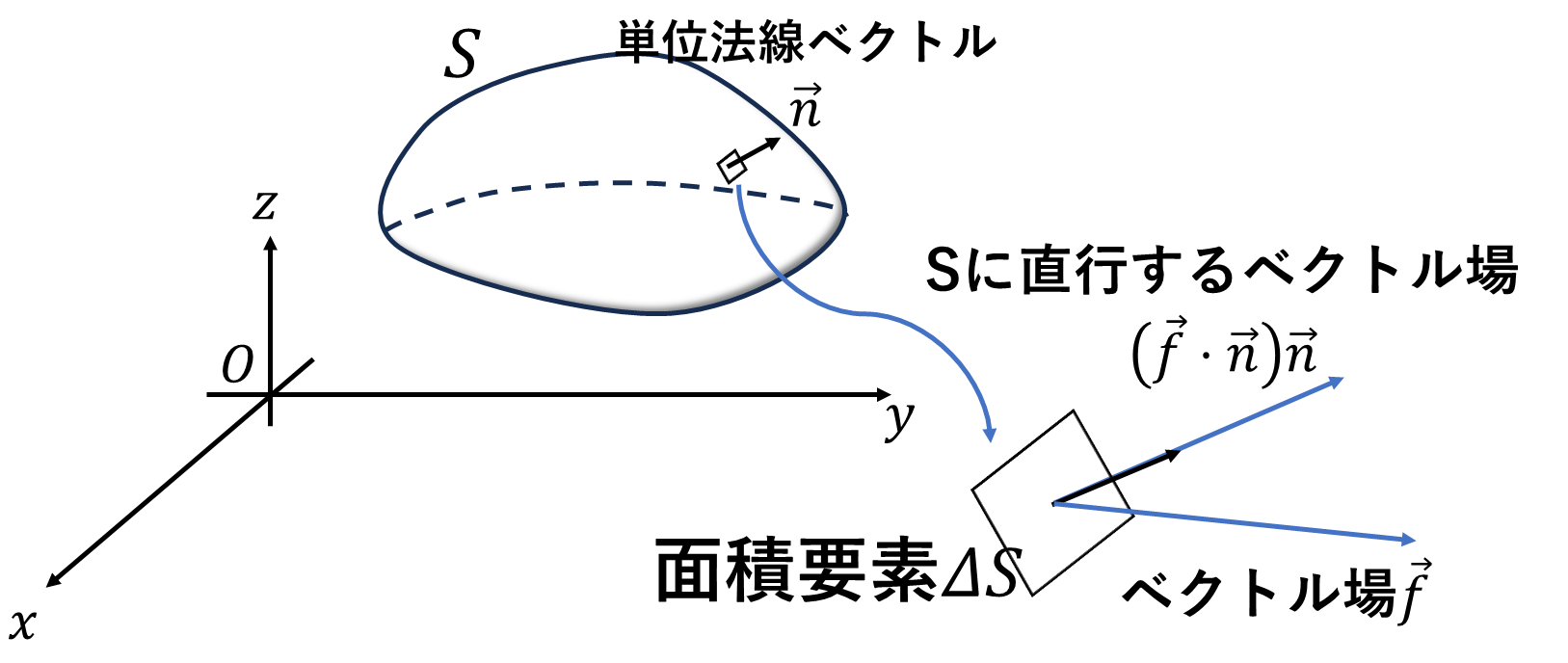
面積分で重要な点は、曲面\(S\)について表面、裏面を一貫して決めることです。曲面\(S\)の各点に表向きの方向に単位法線ベクトル\(\vec{n}\)を取ります。曲面\(S\)上のベクトル場\(\vec{f}=(f^{yz},f^{zx},f^{xy})\)について(つまり\(f^{yz},f^{zx},f^{xy}\)は\(S\)上の任意の点\(p=(x_p,y_p,z_p)\)で決まるスカラー値関数)面積分を次のように定義します。
\[\int_S\vec{f}\cdot \vec{n}dS:=\lim_{n\to\infty}\sum_{i=1}^n\vec{f_i}\cdot\vec{n}_i\varDelta S_i\]
面積要素\(\varDelta S_i\)は\(S\)を\(n\)分割したうちの1つです。記号節約のため\(\varDelta S\)で分割の範囲、分割の面積の大きさの両方表します。\(\vec{f}_i,\vec{n}_i\)は\(\varDelta S_i\)の中での\(\vec{f},\vec{n}\)です。

半径\(a\)の球面\(S\)上のベクトル場
\[\vec{D}(r,\theta,\phi)=\frac{Q}{4\pi r^2}e_r(\theta,\phi)\]
を面積分して見ます。\(\vec{D}\)は点電荷が作る電束密度と呼ばれる物理量です。球面の法線ベクトル\(\vec{n}\)は動径方向の単位ベクトル\(e_r\)に等しいです。\(\vec{n}=e_r\)また\(S\)上では常に\(r=a\)なので、\(\vec{D}\cdot\vec{n}=\frac{Q}{4\pi a^2}e_r\cdot e_r=\frac{Q}{4\pi a^2}\)以上から
\[\int_S\vec{D}(a,\theta,\phi)\cdot\vec{n}dS=\frac{Q}{4\pi a^2}\int_SdS=Q\]
今回はベクトル場と法線ベクトルが平行だったので簡単に積分することができましたが、一般にはそうとは限りません。線積分を積分にしたように面積分は重積分にすることができます。その方法を解説していきます。

曲面上\(S\)の点\(p\)は直交座標であれば、タテ\(x_p\)、ヨコ\(y_p\)高さ\(z_p\)の3つの情報が必要に思われます。しかし、ある変数\(t\)によって曲線を1つ決まり、また別の変数\(u\)によってまた別の曲線が1つ決まる状況を考えれば少なくとも2つの曲線を決めればその交点を\(p\)とすることで、曲面上の点\(p\)は\(t,u\)の2つパラメータで決定できます。緯線と経線を決めるパラメータ2つで、地球表面の点を1つ決めれるみたいな感じです。(ただし変数\(t,u\)によって決められる曲線が一致しないなど、うまいこと曲線を選んであげる必要がありますが、)面積要素\(\varDelta S\)を\(\varDelta t=t_{i+1}-t_i,\varDelta u=u_{j+1}-u_j\)を使って表すこともできます。\(\varDelta t,\varDelta u\)は垂直とは限らないので、ただ積を取るのではなく、平行四辺形とみなして、計算しなくてはなりません。
点\(p\)の位置ベクトルを
\[\vec{r}(t,u)=x(t,u)e_1+y(t,u)e_2+z(t,u)e_3\]
としましょう。更に
\[\varDelta\vec{r}_t:=\vec{r}(t+\varDelta t,u)-\vec{r}(t,u)\]
\[\varDelta\vec{r}_u:=\vec{r}(t,u+\varDelta u)-\vec{r}(t,u)\]
パラメータの変化についての変化量ベクトルを定義します。例えば\(\vec{r}(t+\varDelta t,u)\)は\(\vec{r}(t,u)\)で指定される曲線の次の曲線上の点になるので、\(\varDelta_t\vec{r}\)は曲面\(S\)に沿ったベクトルとなります。\(\varDelta_u\vec{r}\)も曲面\(S\)に沿ったベクトルになるので、\(\varDelta t,\varDelta u\)を十分に小さく取りることでこの2つの変化量ベクトルが作る平行四辺形は面積要素\(\varDelta S\)となります。
\[\varDelta\vec{r}_t=\frac{x(t+\varDelta t,u)-x(t,u)}{\varDelta t}\varDelta te_1\]
\[+\frac{y(t+\varDelta t,u)-y(t,u)}{\varDelta t}\varDelta te_2\]
\[+\frac{z(t+\varDelta t,u)-z(t,u)}{\varDelta t}\varDelta te_3\]
\[\varDelta\vec{r}_t=\frac{\partial x}{\partial t}\varDelta te_1+\frac{\partial y}{\partial t}\varDelta te_2+\frac{\partial z}{\partial t}\varDelta te_3\]
同様にして、
\[\varDelta\vec{r}_u=\frac{\partial x}{\partial u}\varDelta ue_1+\frac{\partial y}{\partial u}\varDelta ue_2+\frac{\partial z}{\partial u}\varDelta te_3\]
となります。3次元空間の2ベクトル\(\vec{a},\ \vec{b}\)が作る平行四辺形の大きさを持つ法線ベクトルは、
\[\vec{S}=\begin{pmatrix}a^2b^3-a^3b^2\\
a^3b^1-a^1b^3\\a^1b^2-a^2b^1\end{pmatrix}\]
で与えられます。\(\varDelta \vec{r}_t,\varDelta \vec{r}_u\)が作る面積要素ベクトルは、
\[\varDelta \vec{S}=\begin{pmatrix}\frac{\partial y}{\partial t}\varDelta t\frac{\partial z}{\partial u}\varDelta u-\frac{\partial z}{\partial t}\varDelta t\frac{\partial y}{\partial u}\varDelta u\\
\frac{\partial z}{\partial t}\varDelta t\frac{\partial x}{\partial u}\varDelta u-\frac{\partial x}{\partial t}\varDelta t\frac{\partial z}{\partial u}\varDelta u\\
\frac{\partial x}{\partial t}\varDelta t\frac{\partial y}{\partial u}\varDelta u-\frac{\partial y}{\partial t}\varDelta t\frac{\partial x}{\partial u}\varDelta u\end{pmatrix}\]
\[=\begin{pmatrix}\frac{\partial y}{\partial t}\frac{\partial z}{\partial u}-\frac{\partial z}{\partial t}\frac{\partial y}{\partial u}\\
\frac{\partial z}{\partial t}\frac{\partial x}{\partial u}-\frac{\partial x}{\partial t}\frac{\partial z}{\partial u}\\
\frac{\partial x}{\partial t}\frac{\partial y}{\partial u}-\frac{\partial y}{\partial t}\frac{\partial x}{\partial u}\end{pmatrix}\varDelta t\varDelta u\]
さらにヤコビアンを使って
\[\varDelta \vec{S}=\left(\frac{\partial(y,z)}{\partial(t,u)}e_1+\frac{\partial(z,x)}{\partial(t,u)}e_2+\frac{\partial(x,y)}{\partial(t,u)}e_3\right)\varDelta t\varDelta u\]
以上から、
\[\int_S\vec{f}\cdot\vec{n}dS=\int_S\left(f^{yz}\frac{\partial(y,z)}{\partial(t,u)}+f^{zx}\frac{\partial(z,x)}{\partial(t,u)}+f^{xy}\frac{\partial(x,y)}{\partial(t,u)}\right)dtdu\]
\(S\)を積分範囲と見ているのであれば、\(S\)を\((t,u)\)による適切な積分範囲に変える必要があります。
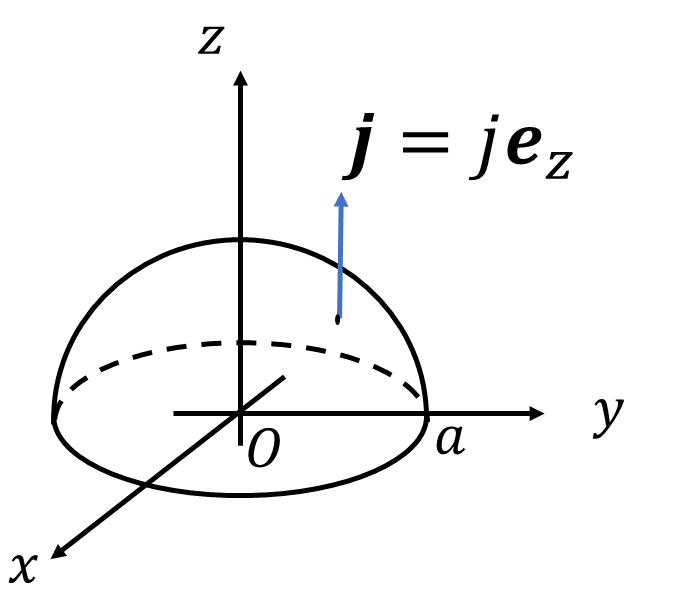
\(z\)方向の定ベクトル\(\vec{j}=0e_1+0e_2+je_3\)を図のような半球で面積分してみます。球面の法線ベクトルは常に動径\((r)\)方向なので、曲面上のベクトル場とみた\(\vec{j}\)との内積\(\vec{n}\cdot\vec{j}\)は一定ではないため計算には工夫が必要になります。ここでさっきの公式を使ってみましょう。
\[\begin{align}\int_S\vec{j}\cdot\vec{n}dS=&\int_S\left(0\frac{\partial(y,z)}{\partial(t,u)}+0\frac{\partial(z,x)}{\partial(t,u)}+j\frac{\partial(x,y)}{\partial(t,u)}\right)dtdu
\\=&j\int_S\frac{\partial(x,y)}{\partial(t,u)}dtdu\end{align}\]
ここでパラメータ\(t,u\)を\(xy\)平面上の極座標\((r,\phi)\)を使ってみましょう。直交座標から極座標へのヤコビアンは\(r\)なので
\[\begin{align}\int_S\vec{j}\cdot\vec{n}dS=&j\int_0^{2\pi}\int_0^a\frac{\partial(x,y)}{\partial(r,\phi)}drd\phi
\\=&j\int_0^{2\pi}\int_0^ardrd\phi
\\=&\pi a^2j\end{align}\]
うまいこと計算することができました。半球の表面で面積分したのに、半球の縁の部分の面積が出てきました。そもそも半球であることを計算で使用しませんでした。この結果は以下のようにすると理解しやすいです。(と思います。)蛇口から水を出す状況を考えます。水流が安定して半径\(a\)円柱状にっている部分を考えます。
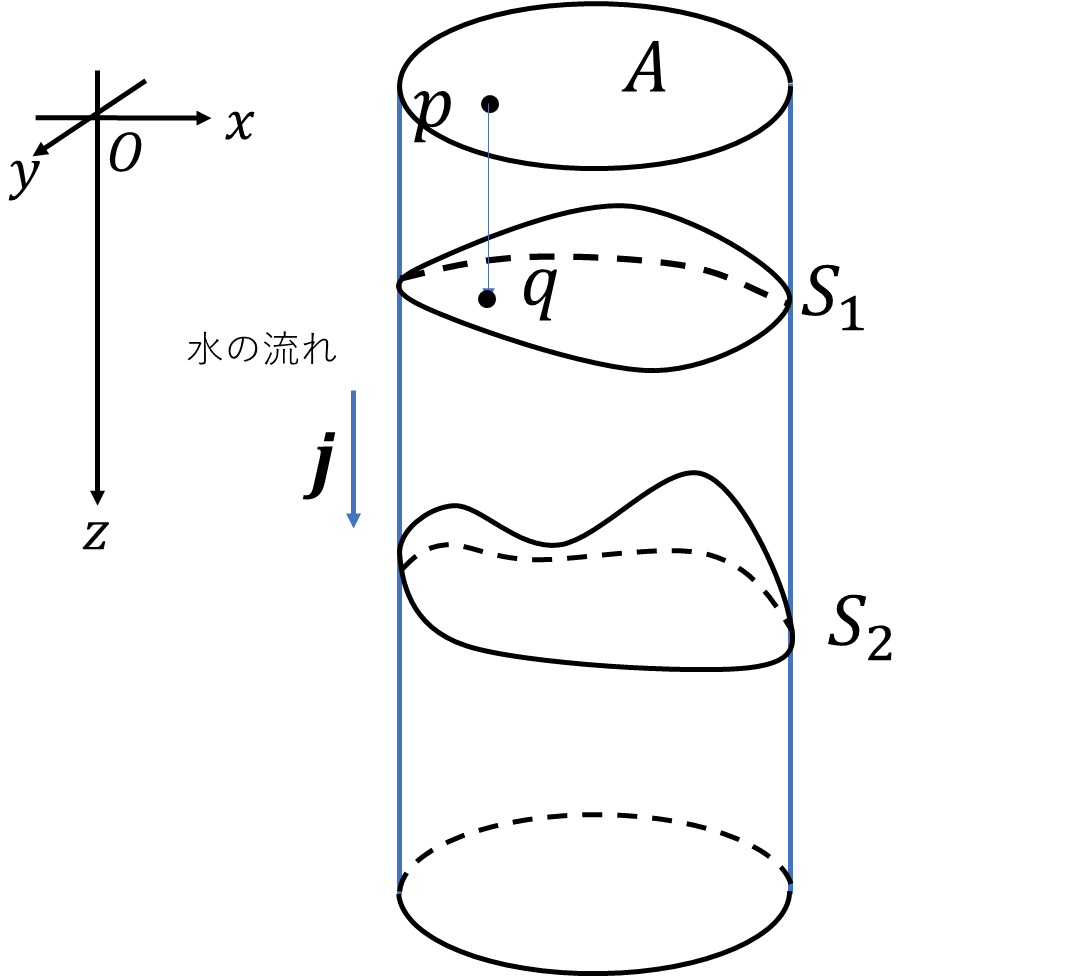
この水の断面を\(A\)、1秒辺りにこの断面を通過する水の体積(流量)を\(I\)とします。(厳密には円柱の縁近くと内側で若干違うかもしれません。)\(j:=I/A\)で定義される流量面密度と水の流れ方向の単位ベクトル\(\vec{n}\)の積で流量密度を定義します。
\[\vec{j}:=j\vec{n}=\frac{I}{A}\vec{n}\]
流量面密度\(\vec{j}\)を水の境界部分を縁とする曲面\(S\)で面積分します。パラメータは\((s,t)=(r,\phi)\)とします。\(r,\phi\)は円\(A\)の中心を原点とする極座標です。
\[\begin{align}\int_S\vec{j}\cdot\vec{n}dS=&\int_S\left(0\frac{\partial(y,z)}{\partial(s,t)}+0\frac{\partial(z,x)}{\partial(s,t)}+j\frac{\partial(x,y)}{\partial(s,t)}\right)dsdt
\\=&j\int_S\frac{\partial(x,y)}{\partial(r,\phi)}drd\phi
\\=&I\end{align}\]
どのような曲面をとっても、その曲面を通過する1秒当たりの水の体積は\(I\)で変わりないと直感的に分かると思います。計算でもそのようになったということです。