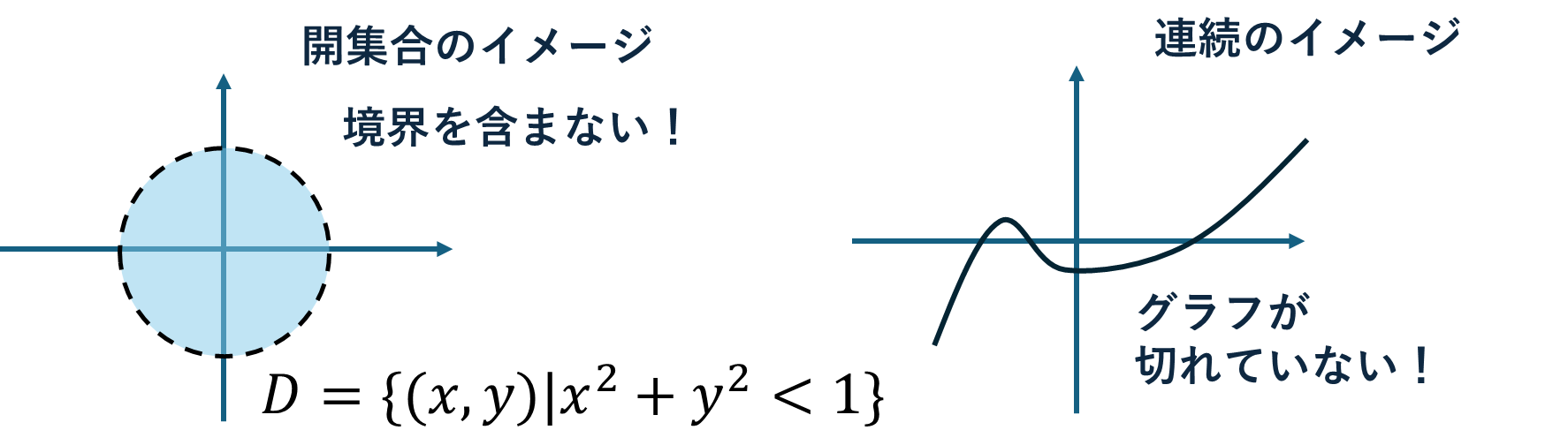楽しい科学（理論）チャンネル

　今まで様々な積分を見てきました。イントロダクションの時より、ストークスの定理までの道筋をより詳細に話せると思います。

・\(\mathbb{R}\)上の関数\(f:\mathbb{R}\to\mathbb{R}\)の積分

・\(\mathbb{R}^2\)上の関数\(g:\mathbb{R}^2\to\mathbb{R}\)重積分の積分

・\(\mathbb{R}^2\)上のベクトル場\(\vec{f}:(x,y)\mapsto(f^1,f^2)\)の線積分

・\(\mathbb{R}^3\)上の関数\(h:\mathbb{R}^3\to\mathbb{R}\)の3重積分

・\(\mathbb{R}^3\)上のベクトル場\(\vec{f}:(x,y,z)\mapsto(f^x,f^y,f^z)\)の線積分

・\(\mathbb{R}^3\)上のベクトル場\(\vec{F}:(x,y,z)\mapsto(f^{yz},f^{zx},f^{xy})\)の面積分

　このグループ分けが何なのかといいますと、線積分はパラメータをうまく見つけることができれば数直線積分に変えられるので、グループ１は数直線上の積分グループです。グループ２は、面積分は２つのパラメータを用いて、２重積分にできるので、２重積分グループ、グループ３は３重積分グループです。関数、ベクトル場何を積分するか？によって、\(m\)重積分、線積分、面積分などを選んでいましたが、 \[\int_\Box\] \(\Box\)に何が入るか？による分類とも見れます。数直線上の区間、曲線は１次元図形の積分です。平面上の開集合、空間の曲面は２次元の図形です。３次元空間の開集合は３次元の図形です。\(\mathbb{R}^2\)上のベクトル場\(\vec{f}:(x,y)\mapsto(f^1,f^2)\)の線積分を例にとってみます。曲線\(C\)は上の任意の点はパラメータ\(t\)によって表せるとします。\(C\)上に限りベクトル場も \[\vec{f}=f^1(x(t),y(t))e_1+f^2(x(t),y(t))e_2\] パラメータ\(t\)だけで表せてしまいます。曲線が１次元の図形であるため、１変数の積分で済んでしまいます。つまり曲線の外の空間が何次元であるかは、積分にはあまり関係ないように見えますね。これから学ぶ多様体というのは図形も表すことができて、基本的に外の空間を仮定しないで、その対象がもつ次元に重点を置いた議論もできるため、多様体を扱いたいのです。多様体のベースには、位相空間の知識が必要になります。

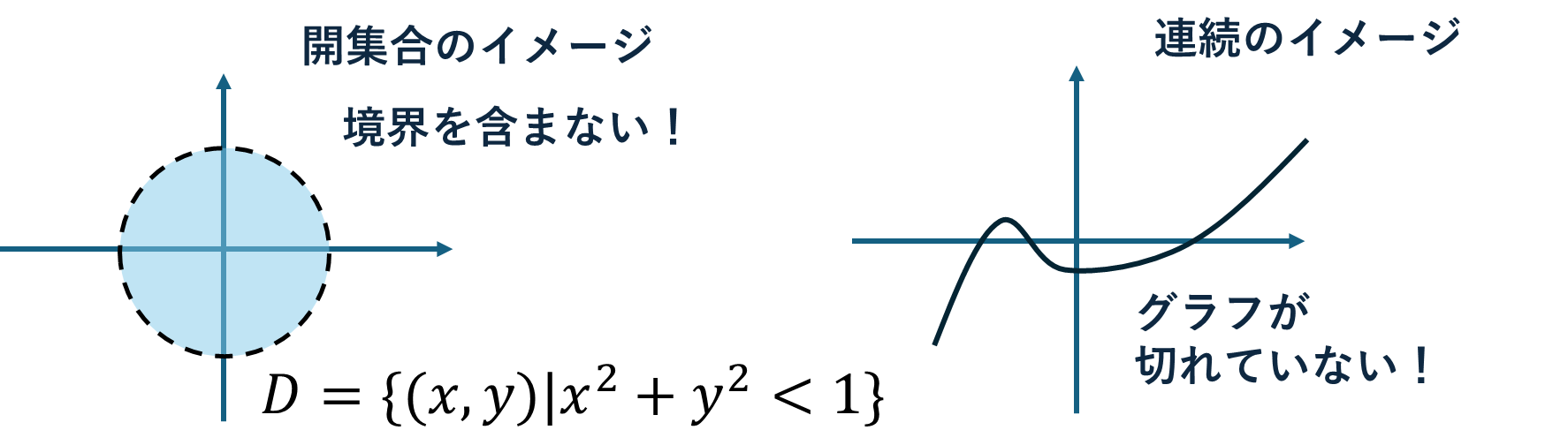
　位相空間では、有限個の要素でも開集合や、連続を定義できて、ユークリッド空間のそれらから性質を取り一般化されています。一度ユークリッド空間でのイメージは捨てなくてはなりません。少しお勉強が必要になります。位相を勉強するモチベーションとして同相という概念があります。円盤や正方形の板、取っ手のない湯呑などを位相という観点から同一視できます。これらの同相な図形などを２次元多様体と呼びます。同相の考え方を応用すれば、２次元多様体上の一部分\(U_i\)の積分は２次元ユークリッド空間上の積分の問題として考えることができます。その部分\(U_i\)が多様体の境界を含むならその境界\(\partial U_i\)は１次元多様体です。

楽しい科学（理論）チャンネル

積分と境界