まずは数学で使う記号を紹介して行きましょう。

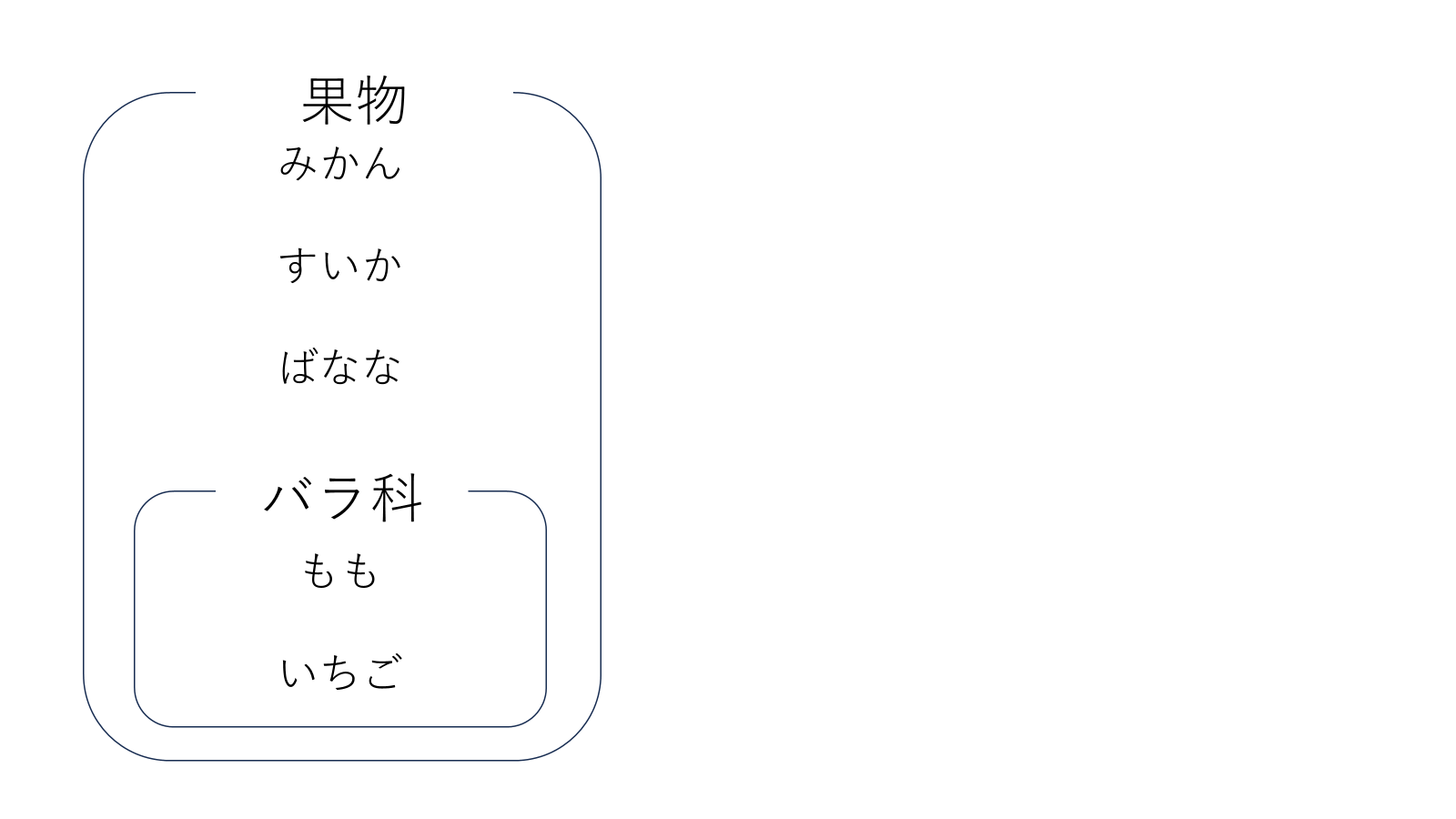
　いくつかの要素の集まりを集合と呼びます。また要素１つ一つのことを元と言います。例えば上記の例で言うと、みかん、すいか、ばなな、もも、いちごがあり、これら５つは果物であり、もも、いちごはバラ科です。みかん、すいか、ばなな、もも、いちごは果物の元で、もも、いちごはバラ科の元です。 \[果物=\{みかん、すいか、ばなな、もも、いちご\}\] これで、『果物の元は、みかん、すいか、ばなな、もも、いちご』という意味になります。 \[バラ科=\{もも、いちご\}\] これは、『バラ科の元は、もも、いちご』という意味になります。またある元が集合の要素であるということを表す記号もあります。 \[みかん\in果物\] これは、『みかんは果物の元である』ことを意味します。 \[もも,いちご\inバラ科\] このように元を複数並べて使うこともできます。これは、『もも、いちごはバラ科の元である』ことを意味します。これと似ていますが、ある集合がさらに大きい集合に含まれるという意味の記号もあります。 \[バラ科\subset果物\] これは、『バラ科は、果物に含まれる』という意味になります。\(いちご\inバラ科\)という表記をした場合はいちごが元で、\(いちご\subsetバラ科\)とした場合は、集合のいちごは、バラ科に含まれるという意味になります。いちごにもいろいろ種類があるのか、それともいちごをそれ以上詳しく考えないかで、この辺の表記は曖昧になります。

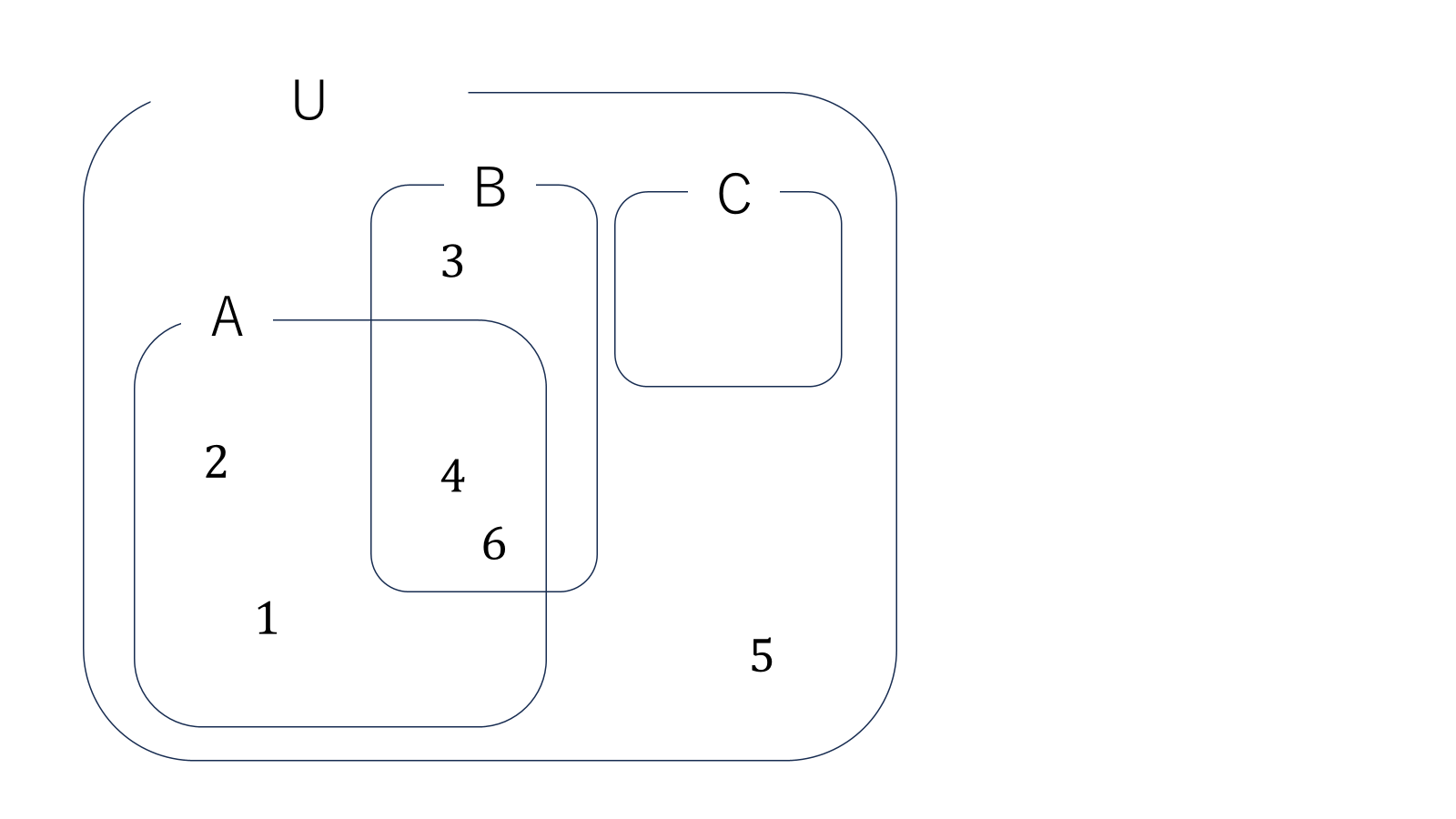
　集合についてイメージが付いたと思いますのでもう少し抽象的にします。\(U,A,B,C\)という集合と\(1,2,3,4,5,6\)という要素があり、 \[U=\{1,2,3,4,5,6\}\] \[A=\{1,2,4,6\},\ B=\{3,4,6\},\ C=\{\}\] のような関係があったとしましょう。集合\(A,B\)の元全てを元とする集合や、集合\(A,B\)どちらにも含まれる元全てを元とする集合を表す記号もあります。これも便利なので紹介します。 \[A\cup B\] この記号は、『\(A\)の元と\(B\)の元全てを元とする集合』を意味します。具体的には、\(A\cup B=\{1,2,3,4,6\}\)です。 \[A\cap B\] は、『\(A,B\)のどちらにも含まれる元全てを元とする集合』を意味します。具体的には、\(A\cap B=\{4,6\}\)です。集合\(U,C\)には特別な名前が付いています。\(U\)のように今考えている状況で一番大きい(外側)の集合を全体集合と言います。\(C\)のように要素を何も含まない集合を空集合と言います。空集合は\(\phi\)を使って表すことが多いです。これらい以外にも、名前の付いた集合をいくつか紹介します。

＊＊有名な集合＊＊

\[\begin{matrix}\mathbb{N}:&自然数全体の集合\\\mathbb{Z}:&整数全体の集合\\\mathbb{Q}:&有理数全体の集合\\\mathbb{R}:&実数全体の集合\\\mathbb{C}:&複素数全体の集合\end{matrix}\]

　\(\mathbb{N}\)は、\(0\)を含む場合と含まない場合があるので注意しましょう。私は小学校で\(0\)を含まないと教わったので、\(0\)を含む場合は、\(\mathbb{N}\cup\{0\}\)と書くことにします。上記の集合は特別に記号が割り振られていますが、便利な表記法を紹介しましょう。 \[A=\{5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\}\] 要は、\(A\)を5以上20以下の自然数の集合としたいわけですが、この表記は長いです。 \[A=\{x\ |\ x\in\mathbb{N},\ 5\le x\le20\}\] このような表記法もあります。2以上3以下の実数の集合のように無限に元があり、元をすべて書き出せない場合は特にこの表記の恩恵を受けることができます。 \[B=\{x\ |\ x\in\mathbb{R},\ 2\le x\le3\}\] または単に、 \[B=\{x\ |\ 2\le x\le3\}\] これで、『集合\(B\)は、２以上３以下の実数全体を表す集合』となります。この表記法を用いることで、和集合\(A\cup B\)、積集合\(A\cap B\)をもっとシンプルに表すことができます。

＊＊和集合、積集合＊＊

　集合\(A,\ B\)の和集合、積集合を以下のように定義する。 \[A\cup B:=\{x\ |\ x\in A\ \mathrm{or}\ x\in B\}\] \[A\cap B:=\{x\ |\ x\in A\ \mathrm{and}\ x\in B\}\]

　せっかくなのでド・モルガンの法則を解説しましょう。

　まず補集合について知る必要があります。補集合\(A^c\)は、全体集合\(U\)から集合\(A\)を除いた部分の集合のことを言います。つまり、\(A^c=\{x|x\notin A\}\)です。\(\notin\)は元ではないという意味です。要はどら焼きという全体集合の部分集合であるあんこの補集合は、２枚のパンケーキの部分になります。この補集合について、 \[(A\cup B)^c=A^c\cap B^c\] \[(A\cap B)^c=A^c\cup B^c\] これがド・モルガンの法則です。

(証明)

　集合\(A,\ B\)について、 \[(A\cup B)^c=\{x\ |\ x\notin (A\cup B)\}\] 「\(x\)が\(A\cup B\)の元でない」のと、「\(A\)の元でないかつ\(B\)の元でない」は同値(同じこと)なので、 \[(A\cup B)^c=\{x\ |\ x\notin A\ \mathrm{and}\ x\notin B\}\] \[=\{x\ |\ x\in A^c\ \mathrm{and}\ x\in B^c\}\] \[=A^c\cap B^c\] \[(A\cap B)^c=\{x\ |\ x\notin (A\cap B)\}\] 「\(x\)が\(A\cap B\)の元でない」のと、「\(A\)の元でない、または\(B\)の元でない」は同値なので、 \[(A\cap B)^c=\{x\ |\ x\notin A\ \mathrm{or}\ x\notin B\}\] \[=\{x\ |\ x\in A^c\ \mathrm{or}\ x\in B^c\}\] \[=A^c\cup B^c\]

(終わり)

＊＊ド・モルガンの法則＊＊

　集合\(A,\ B\)について以下の等式が成り立つ。 \[(A\cup B)^c=A^c\cap B^c\] \[(A\cap B)^c=A^c\cup B^c\]