写像とは何か、関数をイメージしてもらうといいかもしれないです。関数は数字を１つ選ぶと、それに対応した数字を１つだけ教えてくれるものです。これを数字以外にも適応したものが写像です。

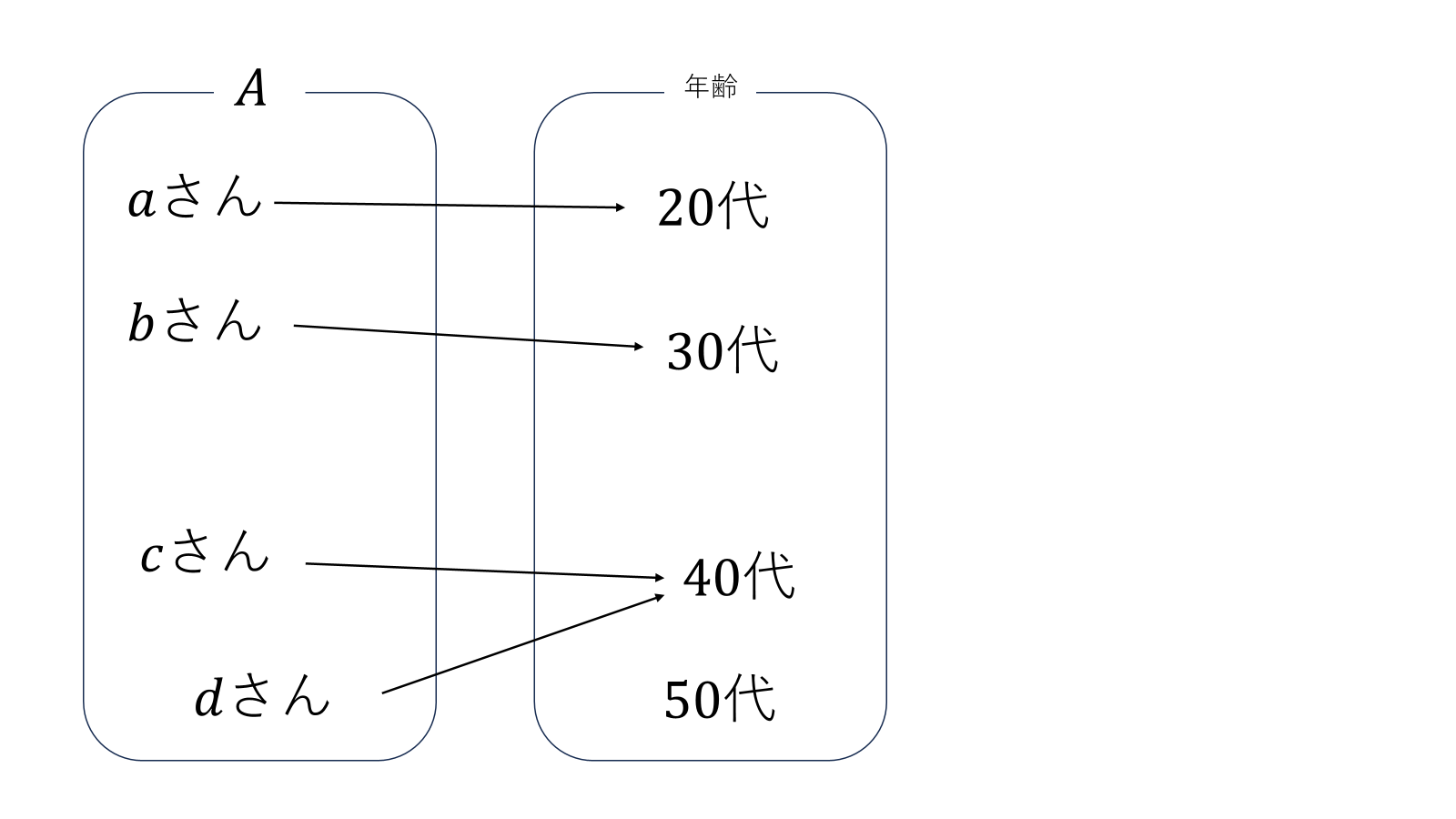
写像の例を1つ出すと、\(a,b,c,d\)の４人の人がいて、\(a\)さんが２０代、\(b\)さんが３０代、\(c,d\)さんが４０代としましょう。この時\(a,b,c,d\)を年齢に対応させる写像を\(f\)とすると、元同士の対応は \[f:aさん\mapsto20代\] \[f:bさん\mapsto30代\] \[f:cさん\mapsto40代\] \[f:dさん\mapsto40代\] のように表記されます。集合同士も写像\(f\)を使って対応させることができます。新たに\(c,d\in C\)となる集合\(C\)を定義して、４０代を集合とみなすと、 \[f:C\to40代\] のように書くこともできます。関数のように\(f(a)=20代,f(C)=40代\)のような表記方法もある。もちろん写像は数字同士を対応させることもでます。 \[f:x\mapsto 2x+3\] であれば、\(f(3)=9\)、\(3\)以上\(5\)未満の実数の集合\(A=\{x\ |\ 3\le x\lt5\}\)については、 \[f(A)=\{y\ |\ 9\le x\lt13\}\] となります。

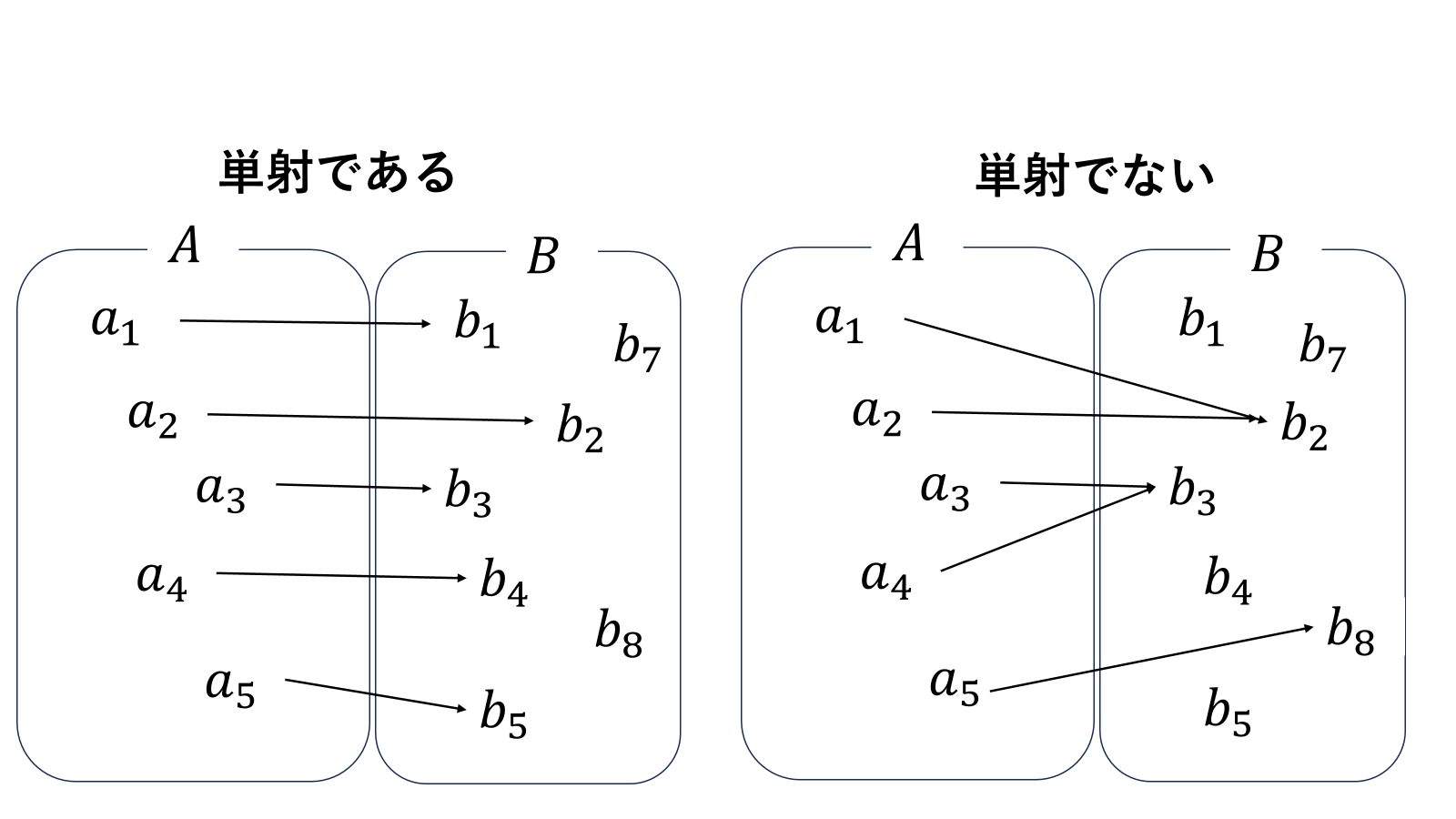
図でみて理解するのが一番楽。単射とは写像の帰り道が1本道であるということです。数学の言葉を使うと \[f:A\to B,\quad x,y\in A\] \[f(x)=f(y)\Rightarrow x=y\] のように表せます。一行目は、\(f\)は集合\(A\)から集合\(B\)への写像であり、\(x,y\)は\(A\)の元であることを表します。２行目は、\(B\)の元\(f(x),f(y)\)が等しいならば、\(x,y\)が一致していることを表します。これが単射の条件です。

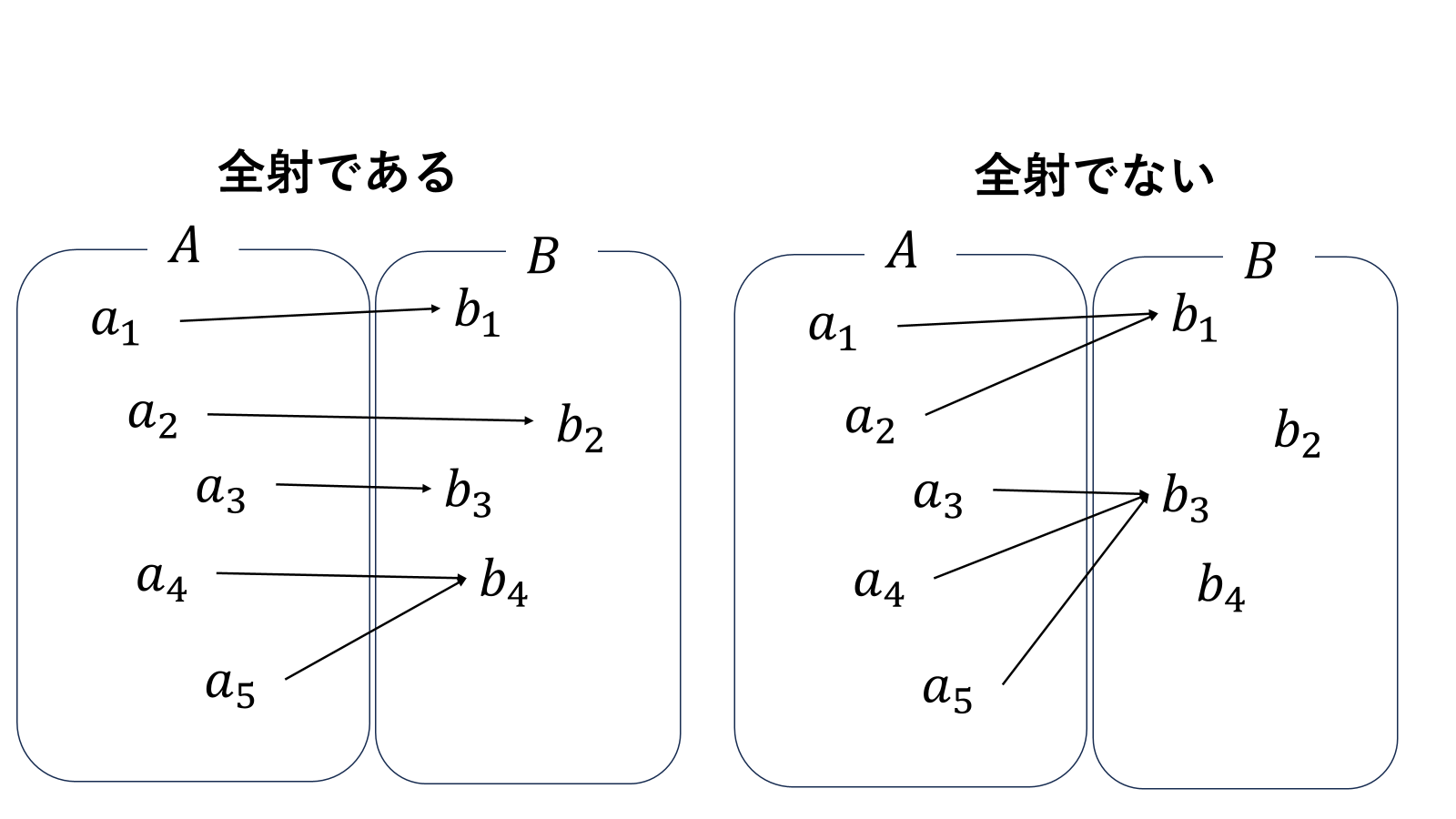
　全射は、写像の先の集合の全ての元が帰り道を持っているということである。数学の言葉を使うと、 \[f:A\to B,\quad x\in A,\ y\in B\] \[\exists x,\ \forall y=f(x)\] \(\exists\)は存在するという意味の記号です。例えば『\(\exists x=3,\ x\in\mathbb{Z}\)は、整数には３が存在する』、『\(\forall x\in \mathbb{R},\ |x|\ge0\)は、全ての実数について絶対値を取ると0以上になる』などの使い方ができます。

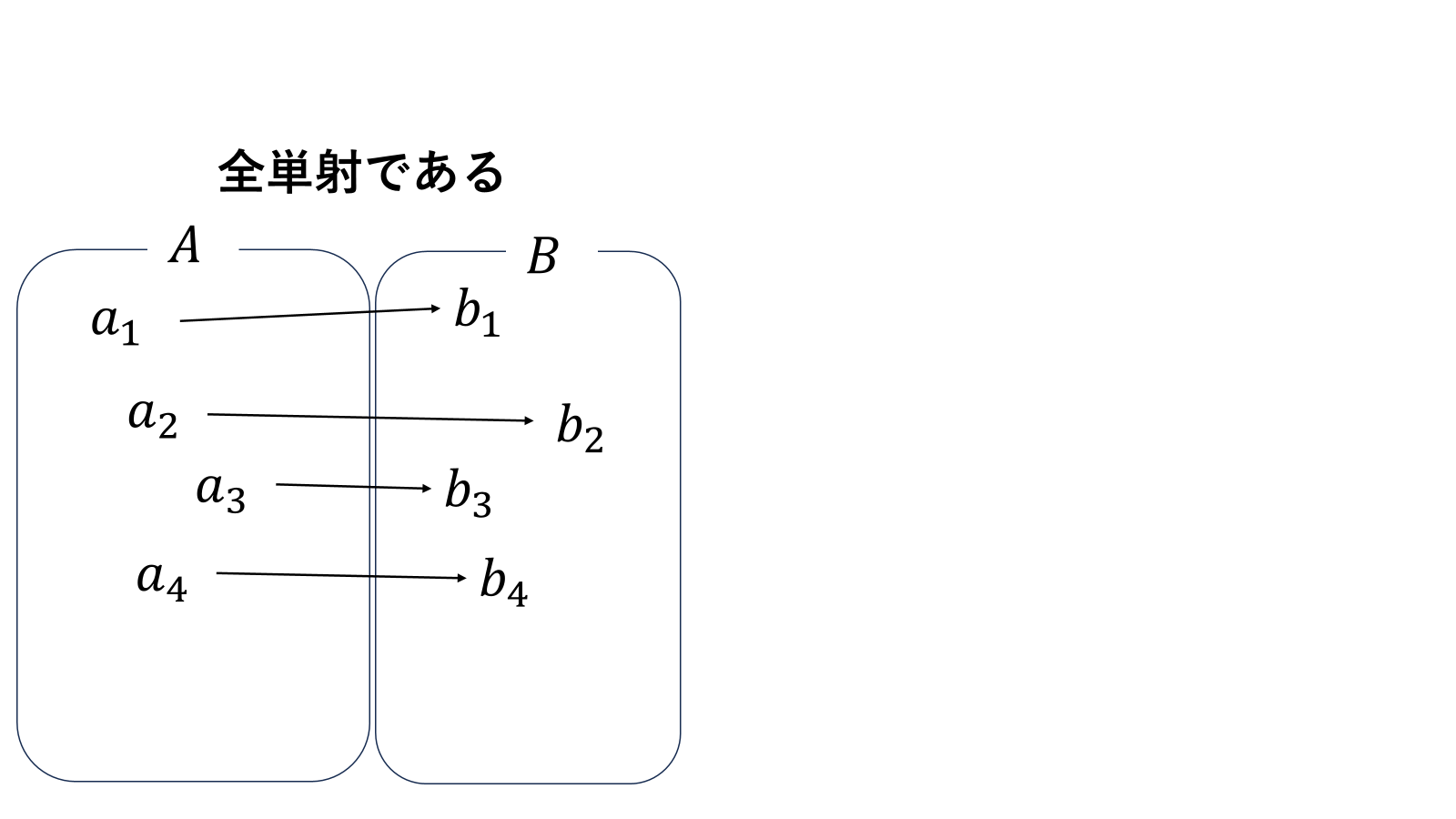
　集合\(A\)から集合\(B\)への写像\(f\)があるなら集合\(B\)から、\(A\)の写像も考えることができます。ただし写像\(f\)が全射かつ単射である必要があります。 \[f^{-1}:B\to A\] \(f\)逆写像は\(f^{-1}\)などと表します。例えば写像\(f\)を \[f:x\to x^2\] とします。

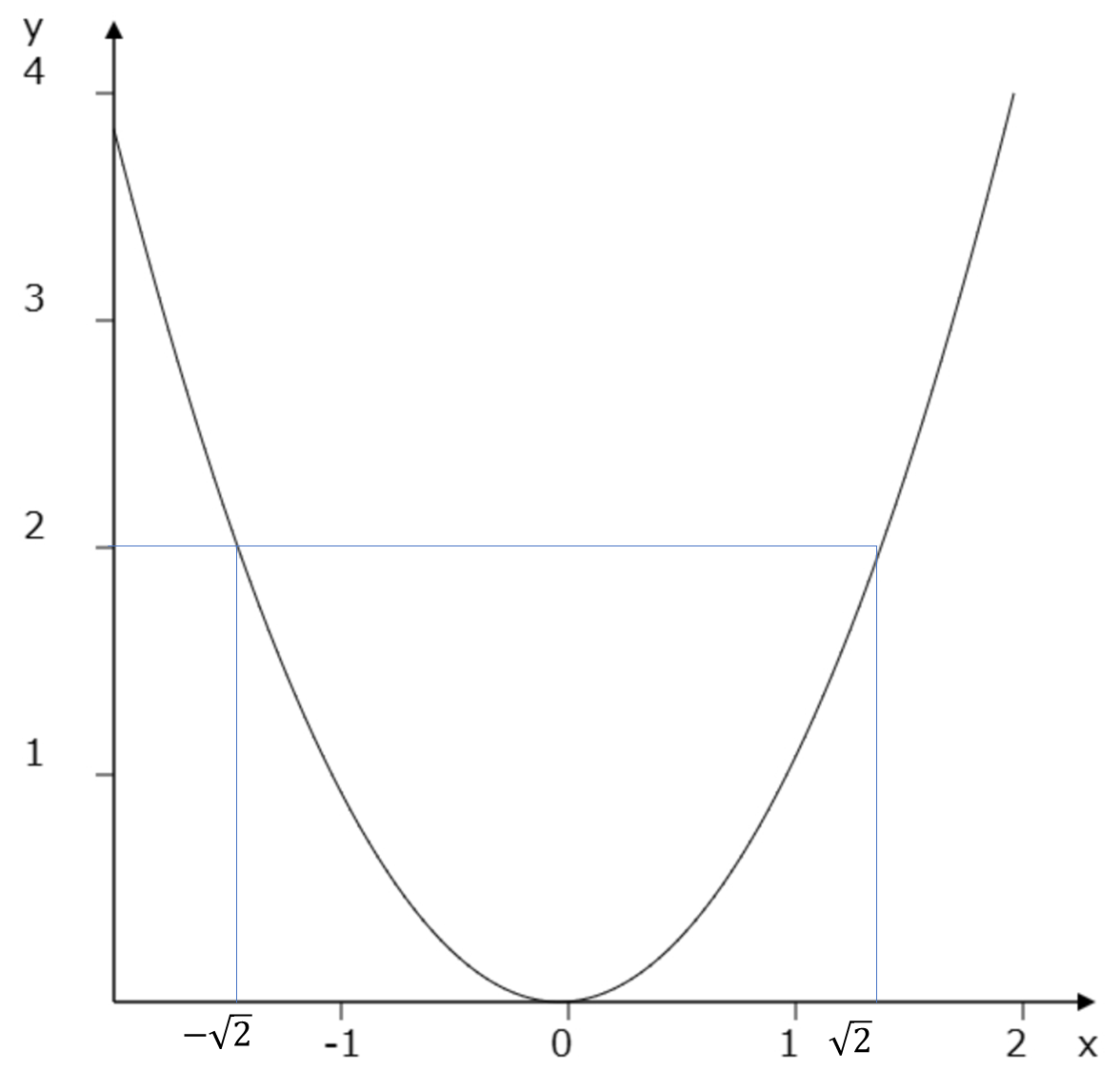
これは全射ではありますが、単射ではありません。なぜなら、\(f(-\sqrt{2})=f(\sqrt{2})=2\)となり\(x\)が１つに定まらないからです。\(x\ge0\)などで全単射になるように定義域を絞ってあげる必要があるわけですね。