このページでは指数関数と対数関数の基本的な考え方を説明していきます。指数関数は \[f:x\to a^x\] の写像のことです。具体的には、\(f(x)=2^x\)などですね。いくつか値を入れてみましょう。 \[f(2)=2^2=4,\ f(3)=2^3=8,\ f(4)=2^4=16\] 手計算では、\(x\)が自然数\(1,2,3\cdots\)の時しか計算できませんが、\(x\)が１増えると、×２という考え方または\(x\)が１つ減るなら÷２するという考え方から \[f(-1)=2^{-2}=\frac{1}{4}\] \[f(-1)=2^{-1}=\frac{1}{2}\] \[f(0)=2^{0}=1\] \[f(1)=2^{1}=2\] \[f(2)=2^{2}=4\] \(x\)が整数の場合まで拡張して写像を考えることができます。今後のためにここで、 \[a^x\] について、\(a\)を底、\(x\)を指数という名を付けておきましょう。\(a^3\)は\(a\)を３回かけたもので、\(a^2\)は\(a\)を２回かけたものなので、 \[a^3\times a^2=a\times a\times a\times a\times a=a^5\] と計算できます。一般に \[a^m\times a^n=a^{m+n}\] が成り立ちます。指数関数の底が同じ数同士の積は指数の足し算で計算できます。\((a^2)^3\)は\(a^2\)を３回かけた数なので、 \[(a^2)^3=a^2\times a^2\times a^2\] 底が同じ指数関数は指数の足し算で計算できるので、 \[(a^2)^3=a^{2+2+2}=a^{2\times3}\] と計算できます。一般に \[(a^n)^m=a^{n\times m}\] が成り立ちます。これを利用して、\(9^{1/2}\)などが計算できるようになります。 \[9^{\frac{1}{2}}=(3^2)^{\frac{1}{2}}=3^{2\times\frac{1}{2}}=3\] しかし、\(2^{1/2},\ 5^{1/2}\)などは計算できません。しかし\(2^{1/2}\)に近い数を探すことはできます。\(2^{1/2}\)というのは２乗したら２になる数ということなので、\(1^2=1\)では小さすぎますし、\(2^2=4\)では大きすぎます。 \[1^2=1\] \[1.4^2=1.96\] \[1.5^2=2.25\] \[2^2=4\] いろいろな数を２乗すると、\(1.4^2=1.96,1.5^2=2.25\)と２に近い数字を見つけることができます。そのため \[2^{\frac{1}{2}}\simeq1.4\] \(1.4\)くらいの数字なのかなと推測できます。ここまでの話で、\(a^x\)の指数\(x\)は\(\frac{1}{n},\ n\in\mathbb{N}\)でもよいことが分かります。これで指数\(x\)を有理数まで拡張できます。例えば、\(3^{4/3}\)なども扱えますね。 \[3^{\frac{4}{3}}=3^{4\times\frac{1}{3}}=(3^4)^{\frac{1}{3}}=81^{\frac{1}{3}}\] 3乗して\(81\)に近い数を探します。 \[4^3=64\] \[4.3^3=79.507\] \[4.4^3=85.184\] \[4.5^3=91.125\] \[5^3=125\] \(3^{4/3}\)は\(4.3\)と\(4.4\)の間くらいだとわかりました。一般に有理数\(p\)を\(p=m/n\ (m,n\in\mathbb{N})\)として、 \[(a^{p})^n=a^{\frac{m}{n}\times n}=a^m\] なので、\(a^p\ (p\in\mathbb{Q})\)は\(n\)回かけて\(a^m\)になる数と定義できます。\(a^x\)の\(x\)は実数\(\mathbb{R}\)で良いそうですが、私にはわかりません。

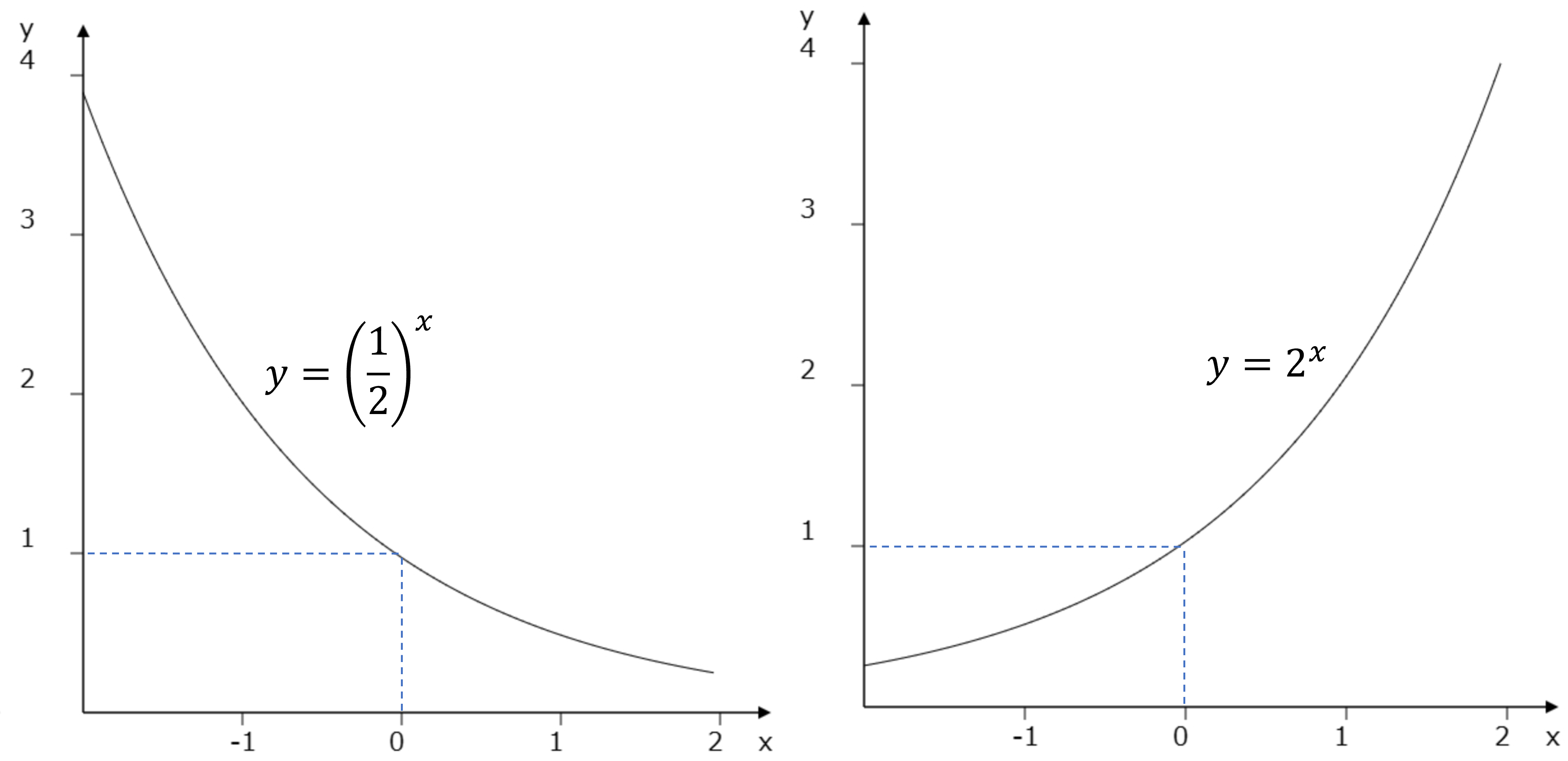
これが指数関数のグラフです。\(y=a^x\)の\(a\)が1より大きいか小さいかで、２パターンあります。\(a\lt 1\)の場合、例えば\(f(x)=(1/2)^x\)などですね。 \[f(1)=\frac{1}{2},\ f(2)=\frac{1}{4},\ f(3)=\frac{1}{8}\] のように減少していく関数になります。次に\(a\gt 1\)の場合です。例えば\(f(x)=2^x\)などですね。 \[f(1)=2,\ f(2)=4,\ f(3)=8\] と単調増加の関数になります。\(a\)が負の数は考えません。複素数の知識が必要になります。

　対数関数は \[f:x\to a^x\] の逆写像です。 \(2^4=16,\ 5^2=25\)なので、 \[\log_216=4,\ \log_525=2\] などと計算するということですね。対数でも\(\log_a\)の\(a\)を底と呼びます。一般に \[\log_aa^n=n\] が成り立ちます。他の対数の計算ルールも見ていきましょう。 まずは \[\log_aa=1\] です。\(a^1=a\)なので、この式が成り立ちます。これにより \[\log_22^2+\log_25\] が計算できます。 \[\log_22^2+\log_22^5=2\log_22+5\log_2\] \[=2+5=7\] 素直に計算すればこうなりますが、さらに \[7=7\log_22=\log_22^7\] \[\log_22^2+\log_22^5=\log_22^7\] となります。一般に \[\log_aa^m+\log_aa^n=m\log_aa+n\log_aa\] \[=(m+n)\log_aa=\log_aa^{m+n}=\log_aa^{m}a^n\] \[\log_aa^m+\log_aa^n=\log_aa^{m}a^n\] \(a^m=A,a^n=B\)とすると、 \[\log_aA+\log_aB=\log_aAB\] これもよく使う計算ですね。\(\log_aA\)を\(n\)回足すと、 \[\overbrace{\log_aA+\log_aA+\log_aA+\cdots\log_aA}^n=n\log_aA=\log_aA^n\] \[n\log_aA=\log_aA^n\] この式も覚えておきましょう。

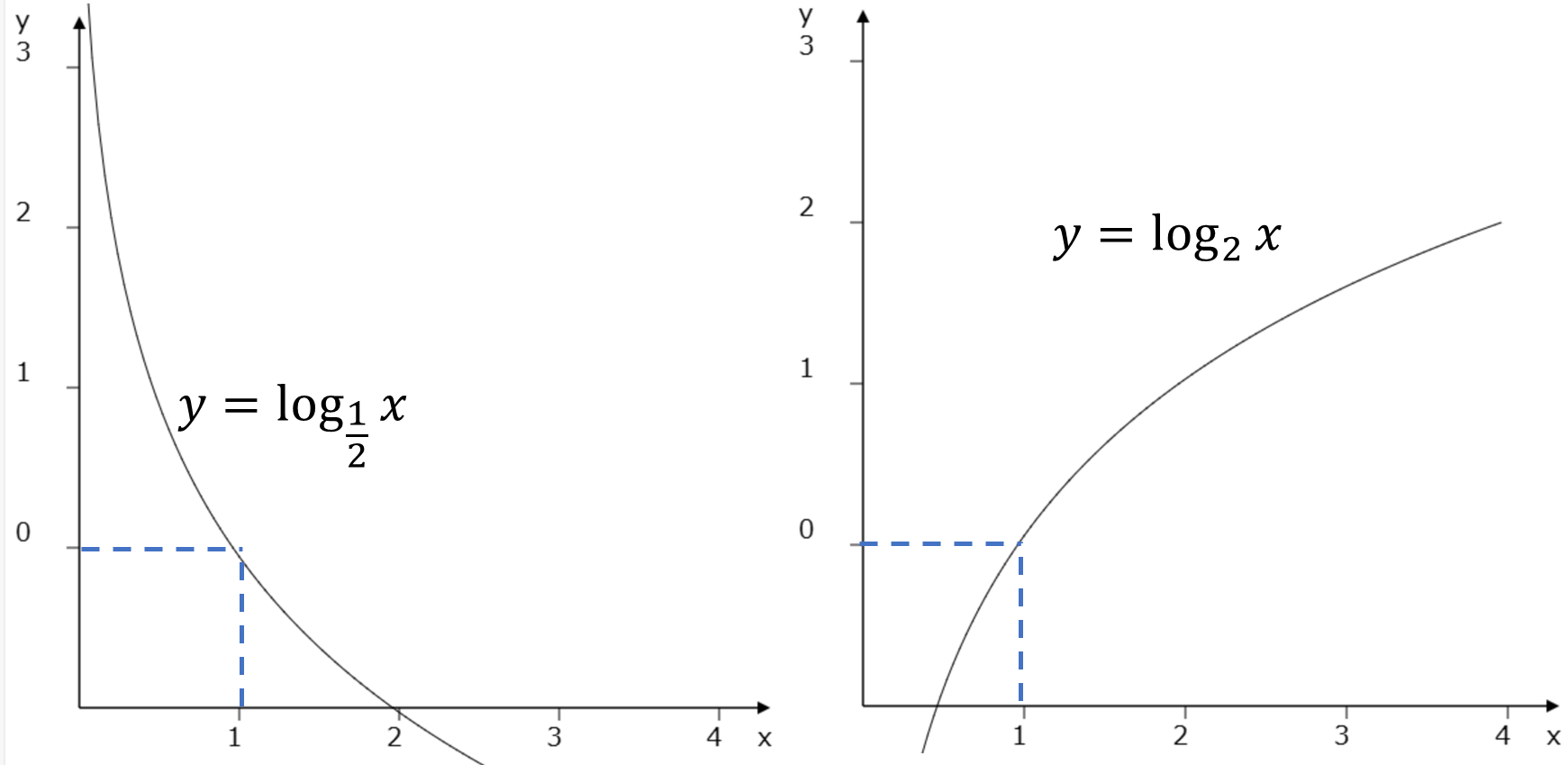
　これが対数関数のグラフです、対数関数\(y=\log_ax\)の底\(a\)が1より大きいか小さいかで２パターンあります。まずは\(a\lt1\)の場合です。例えば\(f(x)=\log_{1/2}x\)などですね。 \[f(1)=0,\ f(2)=-1,\ f(4)=-2,\ f(64)=-6\] のように書くこともできます。関数のように単調減少(減り続ける)関数となっています。\(x=64\)まで進んでも\(y=-6\)なので、\(x\)が大きくなると減少量も緩やかになっていきます。次に\(a\gt1\)の場合ですね。例えば\(f(x)=\log_2x\)を例に取ると、 \[f(1)=0,\ f(2)=1,\ f(4)=2,\ f(64)=6\] となります。こちらは単調増加の関数となっています。\(a\lt1\)に比べ増加する関数になっていますが、\(x\)が大きくなるとグラフが緩やかになるのは一緒ですね。