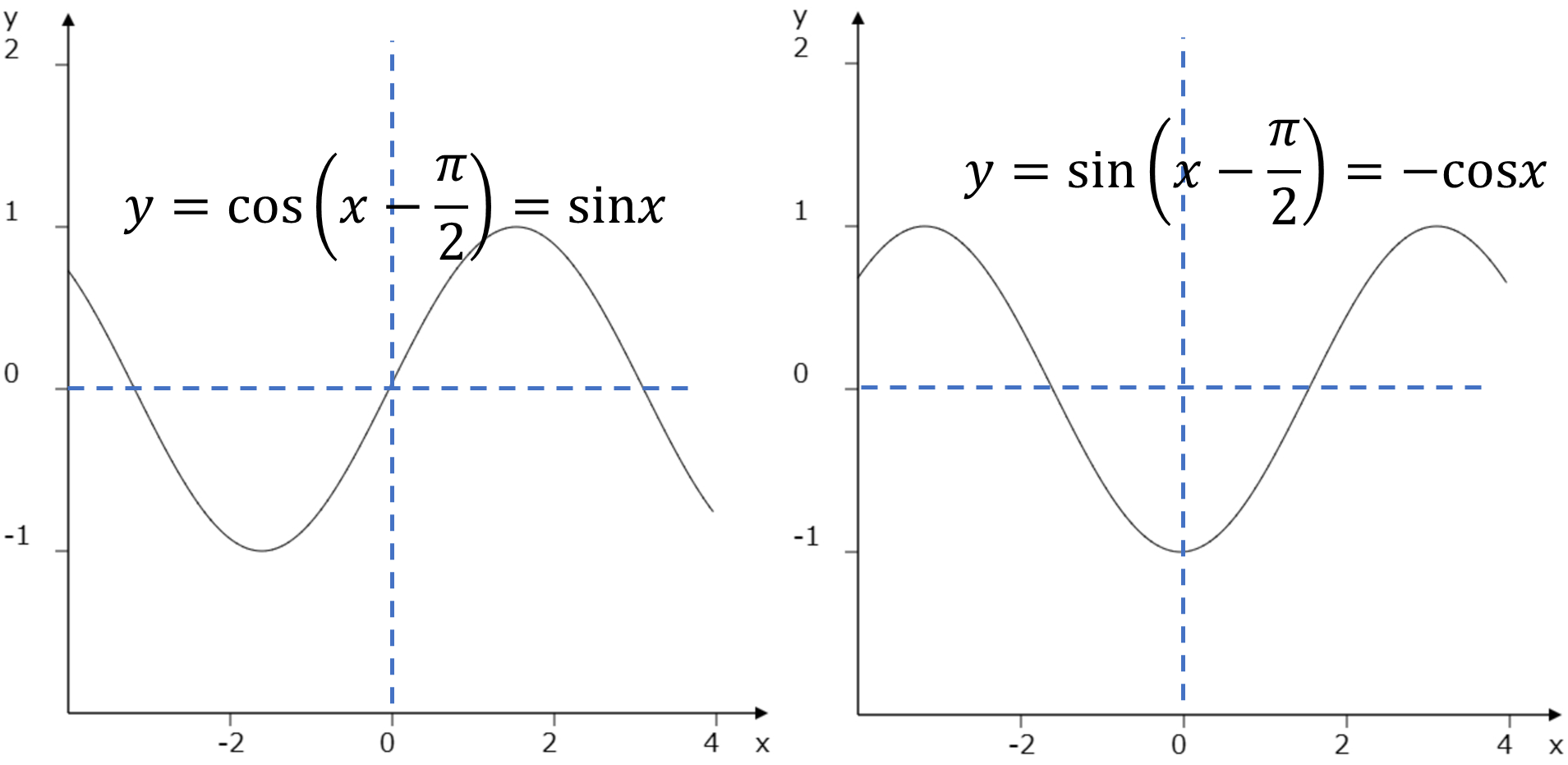楽しい科学(理論)チャンネル
三角関数
弧度法
まず初めに弧度法というものを紹介します。直角を\(90^\circ\)1周を\(360^\circ\)とする度数法はなじみがあると思いますが、弧度法は直角を\(\pi/2\)、1周を\(2\pi\)とする角度の測り方です。\(2\pi=360^\circ\)となります。\(2\pi/360^\circ=1\)なので、
例えば\(30^\circ\)を弧度法で表すと、
\[30^\circ=30^\circ\times1=30^\circ\times\frac{2\pi}{360^\circ}=2\pi\times\frac{30^\circ}{360^\circ}\]
\[=2\pi\times\frac{1}{12}=\frac{\pi}{6}\]
\(45^\circ\)は弧度法で、
\[45^\circ=45^\circ\times\frac{2\pi}{360^\circ}=\frac{\pi}{4}\]
となりますね。なんでわざわざこんなことをするかというと度数法より弧度法のほうがかっこいいからです。冗談です。(笑)弧度法、度数法好きな方を使ってください。
三角比
まずは三角比というものを見ていきましょう。
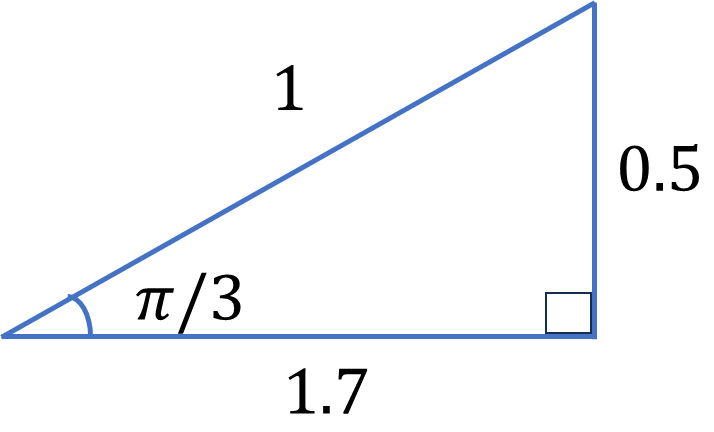
三角比を考える際は、”必ず直角が右、底辺が下”に来るようにしましょう。三角比は斜辺が\(1\)の直角三角形を使って定義するのが良いと思います。例えば\(\pi/3=30^\circ\)の直角三角形について底辺を\(\cos\pi/3\)高さを\(\sin\pi/3\)と決めます。この図でいうと
\[底辺=\cos\frac{\pi}{3}=1.7\]
\[高さ=\sin\frac{\pi}{3}=0.5\]
ぴったり\(\cos\pi/3=1.7\)でないので、\(\cos\pi/3\simeq1.7\)と書くべきですね。\(\simeq\)はだいたい同じという意味です。三角比は特別な角度でなければ求めることは難しいので\(\cos5^\circ\)や\(\sin16^\circ\)はその三角形を書いて定規で測ります。(もしかしたらうまいこと計算できるかもしれませんが、)
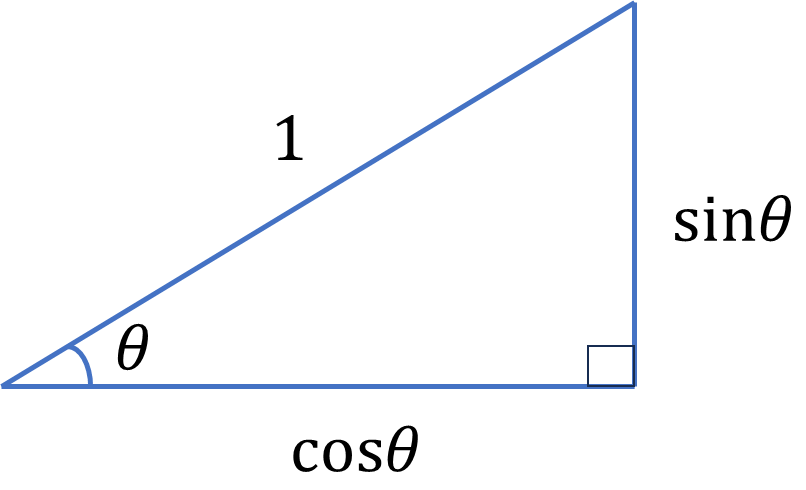
全てこの図に集約されています。まずはこの図を覚えましょう。一般に角度\(\theta\)の直角三角形について、
\[底辺=\cos\theta\]
\[高さ=\sin\theta\]
となっています。三角比には\(\tan\theta\)というのもあり、\(\tan\theta=\sin\theta/\cos\theta\)となっています。
三角関数
先ほど三角比\(\sin\theta,\cos\theta\)を定義しましたが、直角三角形を使った定義であったため、\(0\le\theta\lt \pi/2\)です。つまり、直角を超えることはできませんでした。
そこで単位円(半径が1の円)を使って、半径(=1)を反時計回りにぐるぐる回してみます。この動画は覚えてください。見ないでも思い出せるようにしておきましょう。\(\theta\)は\(x\)軸と半径の間の角で、\(360^\circ=2\pi\simeq6.28\)で一周していることが分かると思います。この半径を\(x\)にまっすぐ降ろしたものを\(\cos\theta\)、\(y\)軸にまっすぐ降ろしたものを\(\sin\theta\)とします。半径を逆回転させることで、負の\(\theta\)も考えることができますね。\(\theta\in\mathbb{R}\)に拡張できました。変数\(x\)について\(\sin x,\cos x\)を写像とみなすこともできます。グラフは次のようになります。\(\theta=0\)のとき\(\cos\)は1、\(\sin\)は0からスタートしています。半径が反時計回りを始めると、\(\cos\)は減少し始めて、\(\sin\)は増加していきます。動画の\(\sin,\ \cos\)とグラフが対応していることも確認しておきましょう。
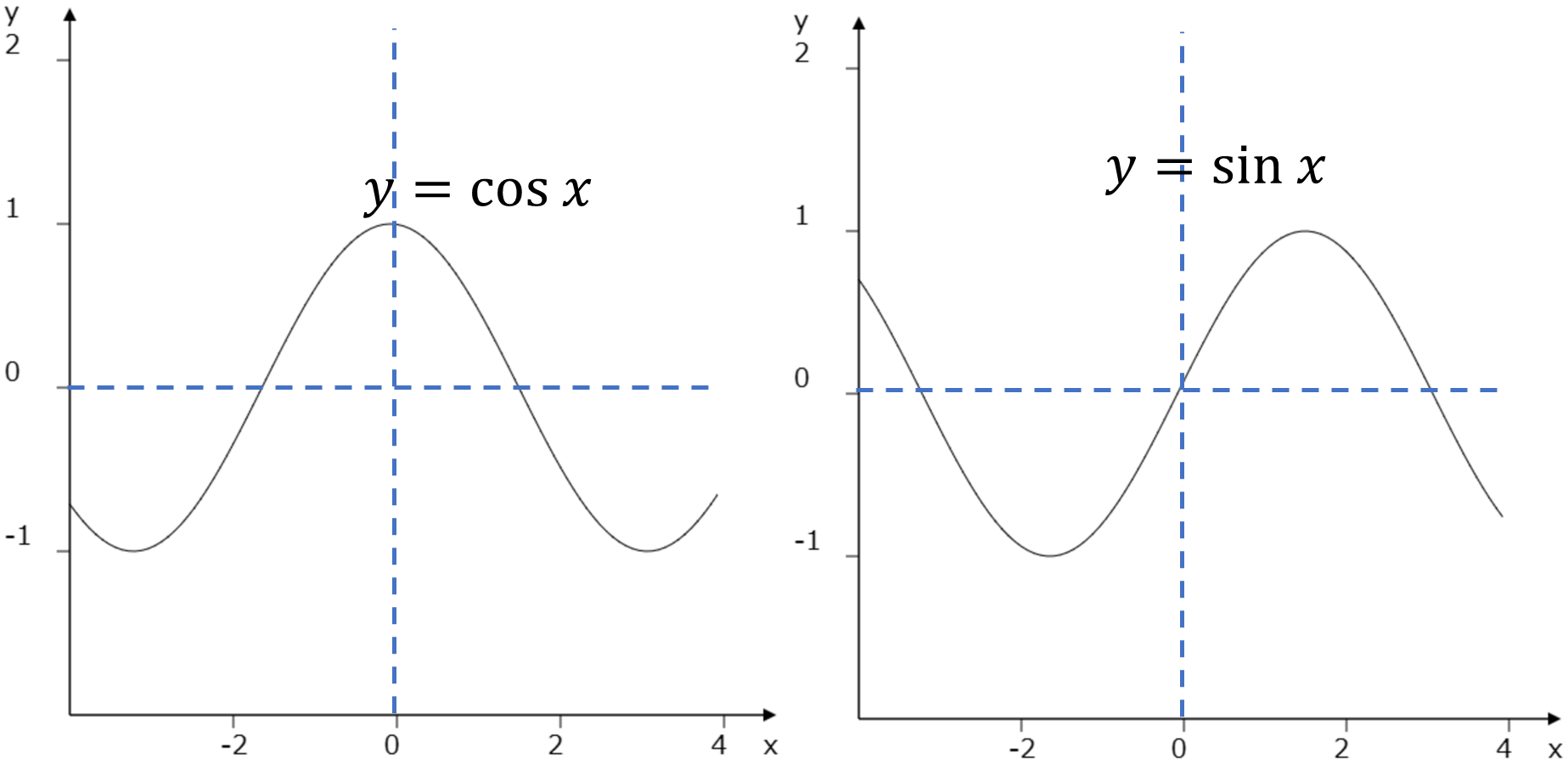
三角比の性質
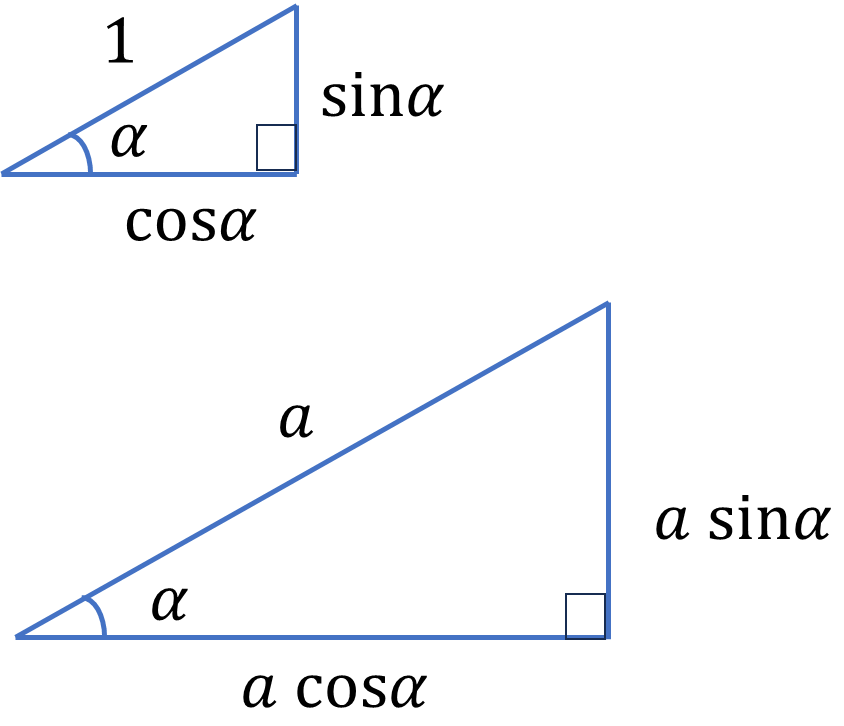
まずは角度\(\alpha\)の直角三角形を\(a\)倍に拡大します。辺の長さも全て、\(a\)倍になるので、斜辺が\(a\)直角三角形の底辺と斜辺は
\[底辺=a\cos\alpha\]
\[高さ=a\sin\alpha\]
となります。
直角三角形では、ピタゴラスの定理(三平方の定理)により
\[底辺^2+高さ^2=斜辺^2\]
となります。斜辺1の直角三角形は底辺\(=\cos\theta\)、高さ\(\sin\theta\)と表せるため、
\[\cos^2\theta+\sin^2\theta=1\]
となります。\((\cos\theta)^2\)は\(\cos\theta^2\)と書くと角度\(\theta\)を2乗してから\(\cos\)関数に代入して見えてしまうため、\((\cos\theta)^2=\cos^2\theta\)と表記する決まりになっています。これにより
\[\tan^2\theta=\frac{\sin^2\theta}{\cos^2\theta}=\frac{1-\cos^2\theta}{\cos^2\theta}\]
\[\tan^2\theta=\frac{1}{\cos^2\theta}-1\]
これもよく見る式ですね。
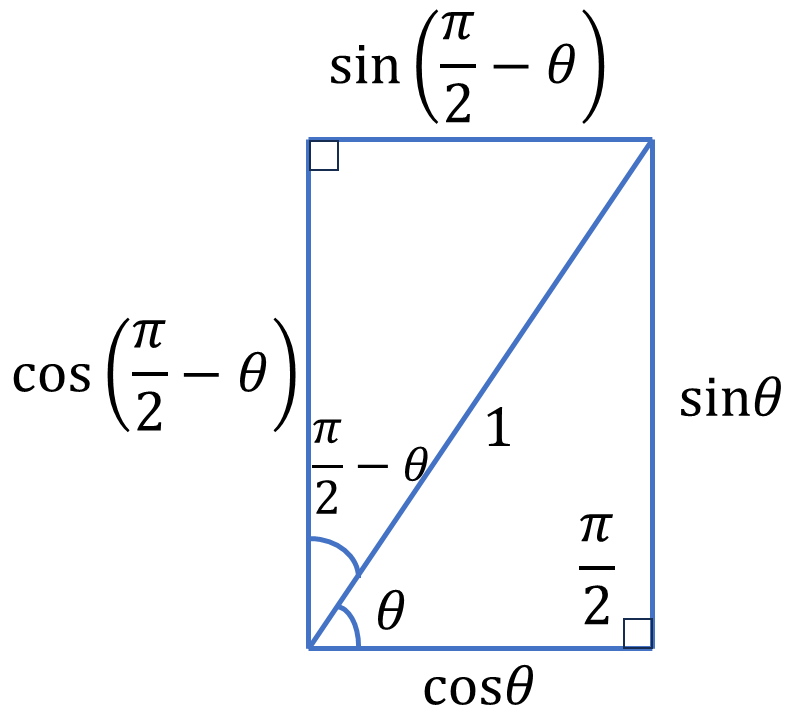
この図を見てもらうと分かると思いますが、
\[\cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta\]
\[\sin\left(\frac{\pi}{2}-\theta\right)=\cos\theta\]
です。これもたまに使う性質ですね。
三角関数の性質
三角関数を定義した動画を思い出してもらえば分かりますが、円の半径の2乗は\(x\)座標の2乗と\(y\)座標の2乗の和になるので、
\[r^2=x^2+y^2\]
\(r=1\)の時の\(x\)座標は\(\cos x\)、\(y\)座標は\(\sin x\)なので、\(\theta\in\mathbb{R}\)について、
\[\cos^2\theta+\sin^2\theta=1\]
が成り立ちます。
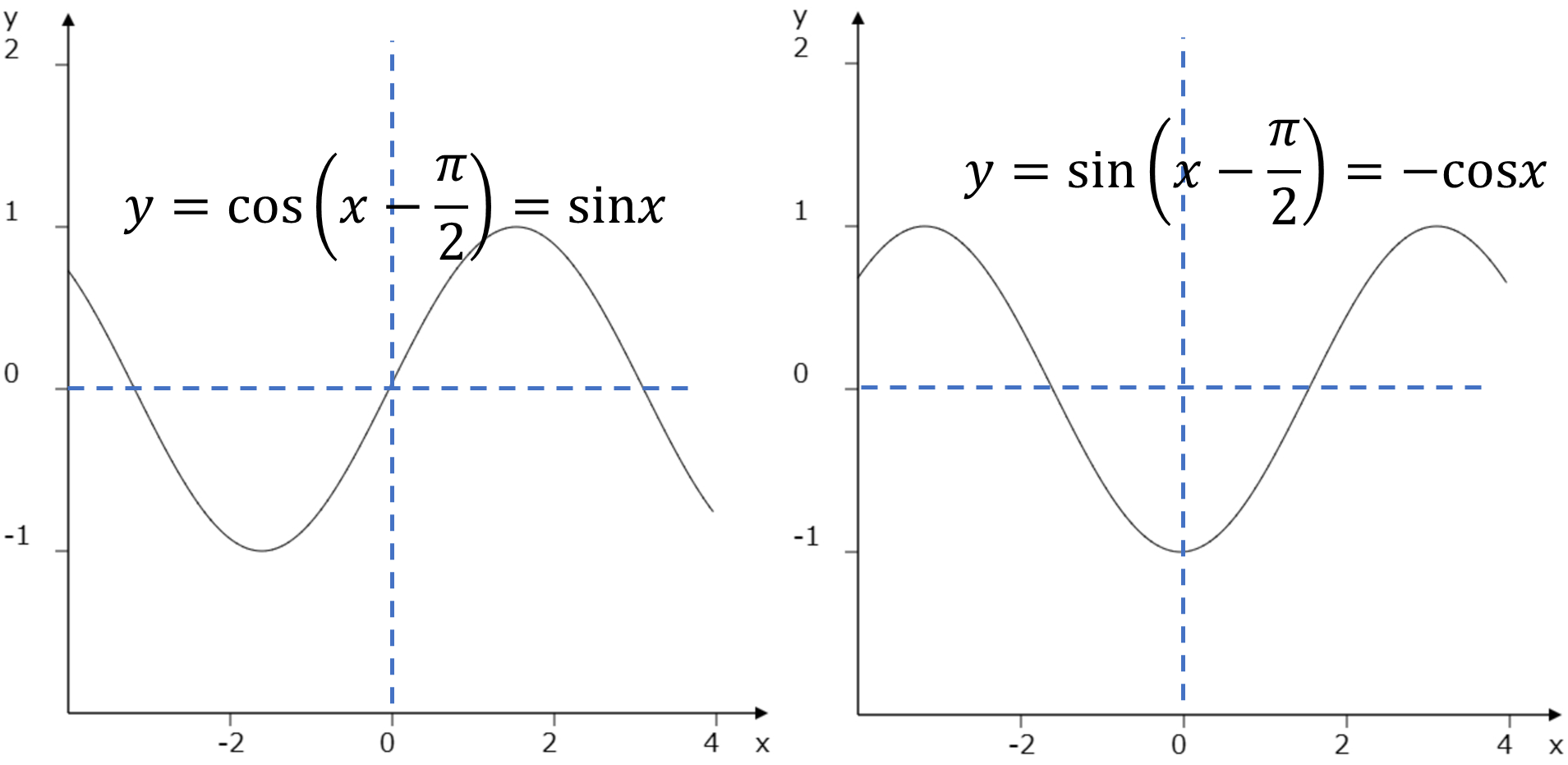
この図から以下のことが分かります。三角関数のグラフを\(\pi/2\)だけグラフを平行移動したら
\[\cos\left(x-\frac{\pi}{2}\right)=\sin x\]
\[\sin\left(x-\frac{\pi}{2}\right)=-\cos x\]
となります。この性質はとても大切なので覚えてください。グラフの平行移動が分からない方は、三角関数の定義で暗記してもらった動画がありますよね。\(\pi/2\)つまり直角からスタートすれば同様の結果になります。次に\(\pi/2\)の平行移動を4回行ってみます。
\[\cos\left(x-2\pi\right)=\cos\left(\left(x-\frac{3\pi}{2}\right)-\frac{\pi}{2}\right)\]
\[=\sin\left(x-\frac{3\pi}{2}\right)\]
\[=\sin\left(\left(x-\frac{2\pi}{2}\right)-\frac{\pi}{2}\right)\]
\[=-\cos\left(x-\frac{2\pi}{2}\right)\]
\[=-\cos\left(\left(x-\frac{\pi}{2}\right)-\frac{\pi}{2}\right)\]
\[=-\sin\left(x-\frac{\pi}{2}\right)\]
\[\cos\left(x-2\pi\right)=\cos x\]
\(\sin x\)も\(\pi/4\)の平行移動を4回やります。
\[\sin\left(x-2\pi\right)=-\cos\left(x-\frac{3\pi}{2}\right)\]
\[-\sin\left(x-\frac{2\pi}{2}\right)=\cos\left(x-\frac{1\pi}{2}\right)\]
\[\sin\left(x-2\pi\right)=\sin x\]
\(x\)軸方向の\(2\pi\)の平行移動は、暗記してもらった動画でいうと半径の1回転に当たるので、もとの関数に戻るということですね。一般に\(n\in\mathbb{Z}\)(整数)を使って
\[\cos(x+2\pi n)=\cos x\]
\[\sin(x+2\pi n)=\sin x\]
2,3,4回転しようが、-1,-2回転しようが同じように成り立ちます。これを三角関数の周期性と言ったりもします。この場合周期は\(2\pi\)です。また途中式から、
\[\cos(x+(2n+1)\pi)=-\cos x\]
\[\sin(x+(2n+1)\pi)=-\sin x\]
半周期\(\pi\)のずれで三角関数は符号が逆になります。1周期\(2\pi\)で元に戻るので\(\pi\)奇数回のずれで符号が逆になるということです。
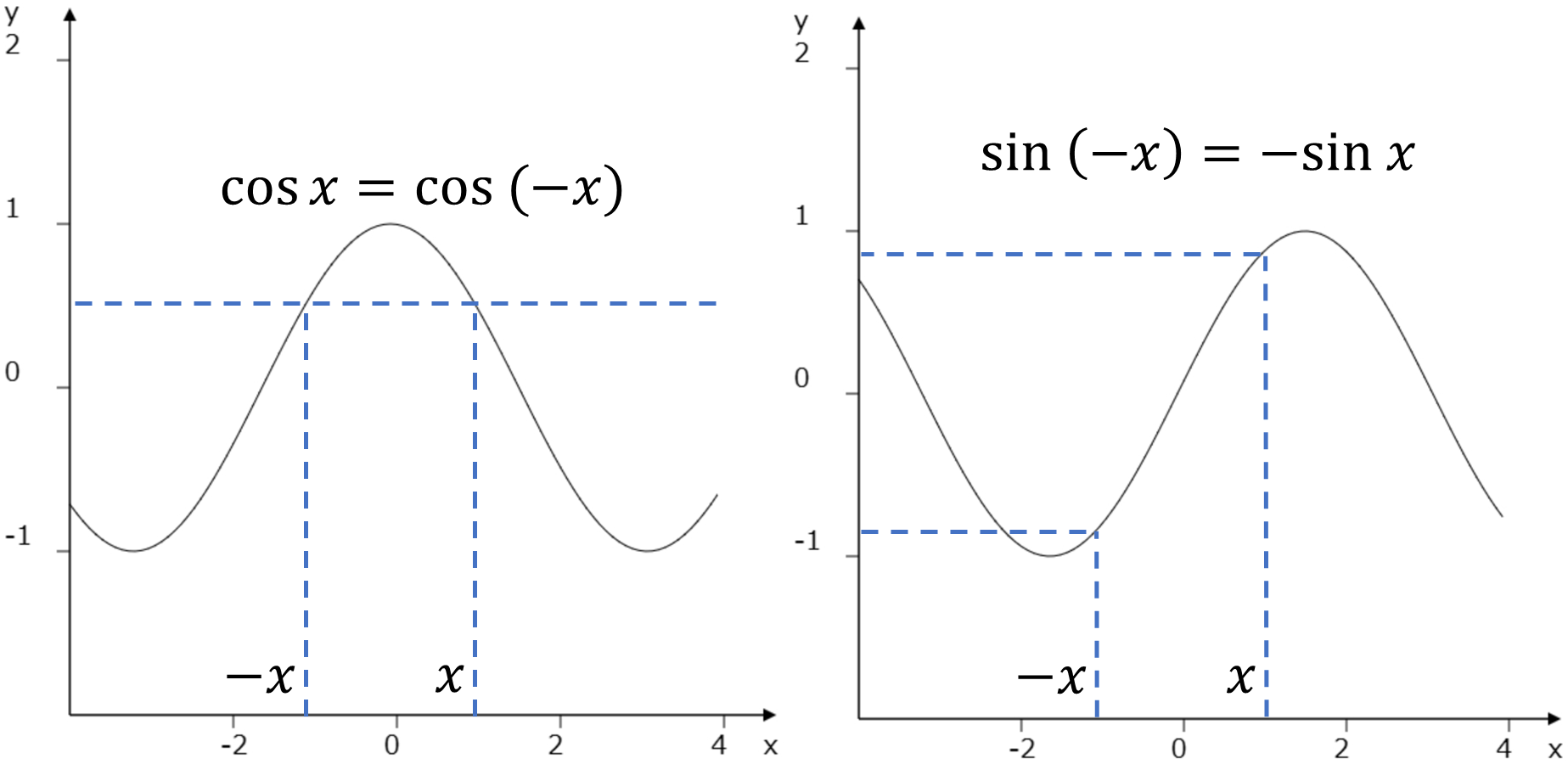
次の性質です。
\[\cos x=\cos(-x)\]
これは図より明らかですね。\(\sin\)の方はぱっと見分からないので、示していきましょう。この式の\(x\)を\(x-\pi/2\)に置き換えます。\(x\to x-\pi/2\)
\[\cos\left(x-\frac{\pi}{2}\right)=\cos\left(-x+\frac{\pi}{2}\right)\]
\(\cos\)の中身から\(2\pi\)を引いても変わらないので、右だけ引きます。
\[\cos\left(x-\frac{\pi}{2}\right)=\cos\left(-x-\frac{3\pi}{2}\right)\]
\[\sin x=\sin\left(-x-\frac{2\pi}{2}\right)=-\cos\left(-x-\frac{1\pi}{2}\right)\]
以上より
\[\sin x=-\sin (-x)または-\sin x=\sin (-x)\]
\(\sin\)は中身の符号を変えたものと元々の関数の符号を変えたものが等しいということですね。
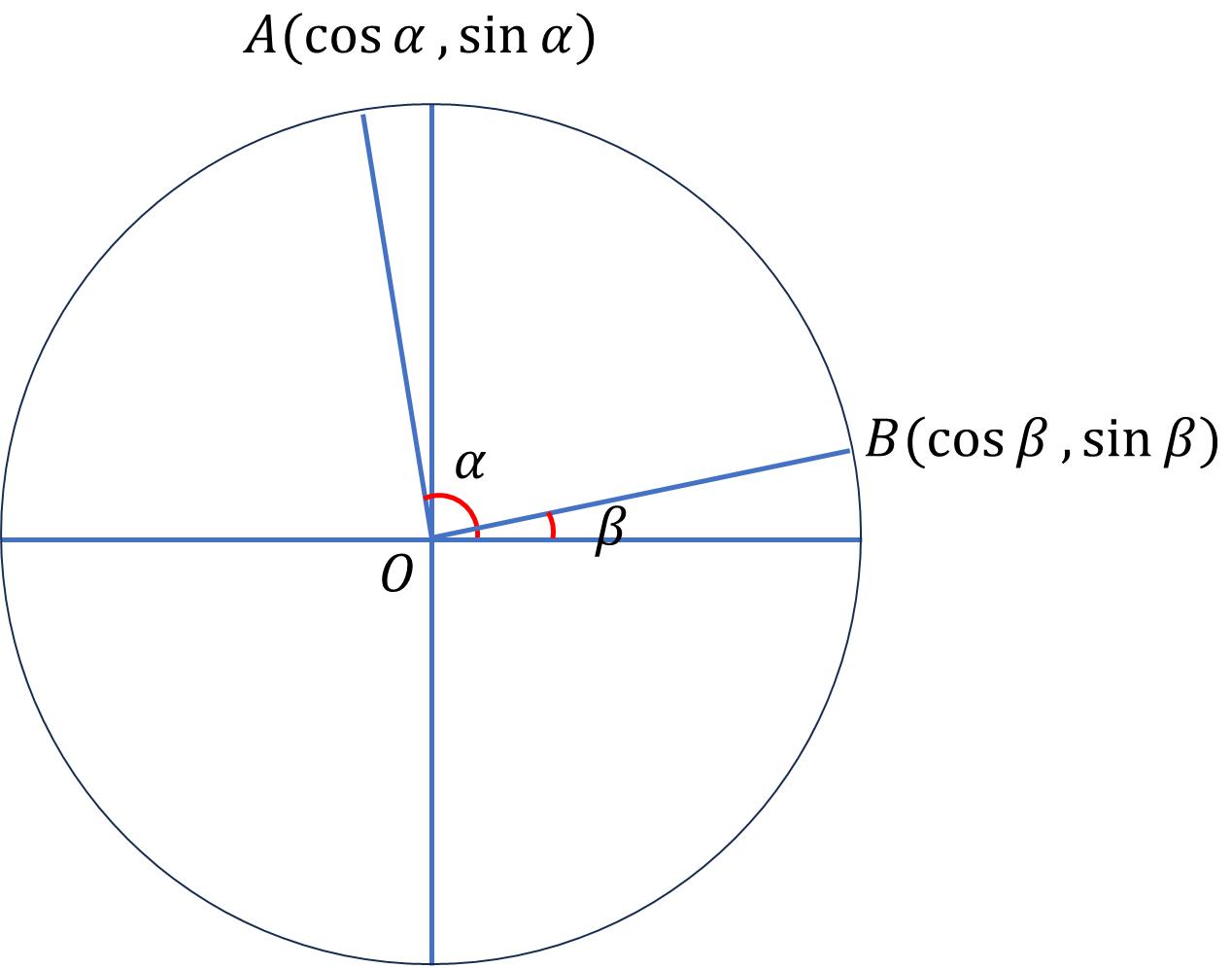
ありがちな証明ですがこの図を使って加法定理を証明していきます。円の半径(OA=OB=1)です。まずは余弦定理から、
\[AB^2=OA^2+OB^2-2OA\ OB\cos(\alpha-\beta)\]
\[=2-2\cos(\alpha-\beta)\]
\(A\)、\(B\)間の距離は、
\[AB^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\cos\beta)^2\]
\[=2-2\cos\alpha\cos\beta+\sin\alpha\cos\beta\]
以上より、
\[\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\]
\(\beta\mapsto-\beta\)と置き換えて、
\[\cos(\alpha+\beta)=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\]
\[\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\]
これが余弦の加法定理というものです。更に\(\alpha\mapsto\alpha-\pi/2\)と置き換えれば、
\[\cos\left(\alpha+\beta-\frac{\pi}{2}\right)=\cos\left(\alpha-\frac{\pi}{2}\right)\cos\beta-\sin\left(\alpha-\frac{\pi}{2}\right)\sin\beta\]
\[-\sin(\alpha+\beta)=-\sin\alpha\cos\beta-\cos\alpha\sin\beta\]
\[\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\]
正弦の加法定理も証明終わりです。