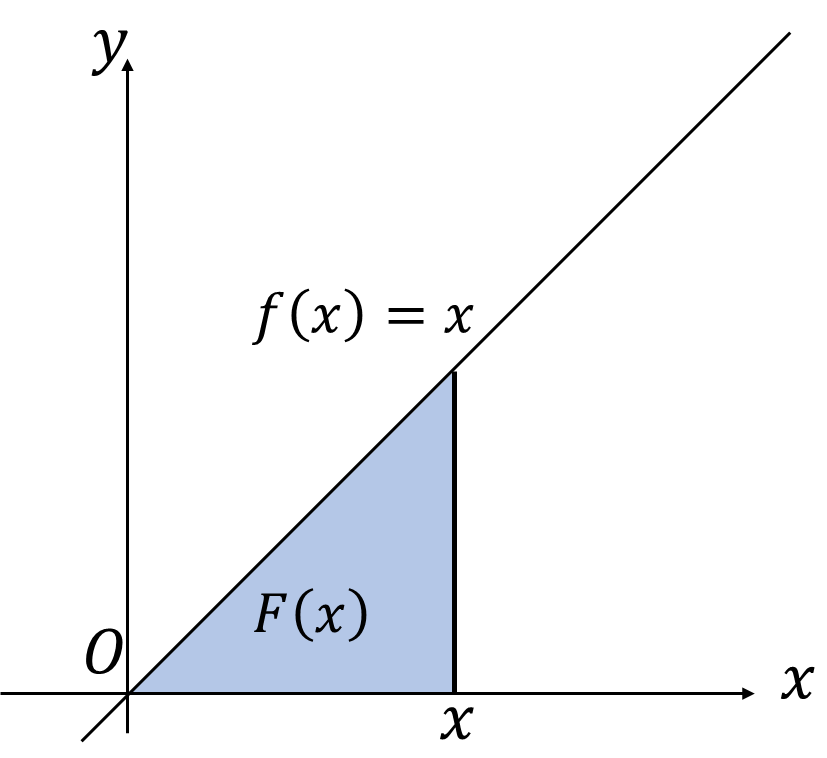楽しい科学(理論)チャンネル
微分積分学の基本定理
極限
微積分で使う記号を紹介していきます。まずは極限\(\lim\)です。
\[\lim_{y\to3} (y+5)=3+5=8\]
\(\lim\)の下についている\(y\to3\)は\(y\)を\(3\)に近づけるという意味です。極限の計算の注意点です。
\[\lim_{h\to1}\frac{1-h^2}{1-h}=\frac{1-1}{1-1}=\frac{0}{0}\]
とはなりません。
\[\lim_{h\to1}\frac{1-h^2}{1-h}=\lim_{h\to1}\frac{(1-h)(1+h)}{1-h}\]
\[=\lim_{h\to1}(1+h)=2\]
ある程度式を簡潔にしてから極限を取るといいです。
\[\lim_{x\to3}\frac{|x-3|}{x-3}\]
のような極限も注意が必要です。3より大きいほうから3極限を取るか3より小さいほうから極限を取るかで値が変わります。
\[\lim_{x\to3+0}\frac{|x-3|}{x-3}=\lim_{x\to3+0}\frac{x-3}{x-3}=1\]
\(x\to3+0\)は右から極限を取ることを意味していて右極限と言います。\(x\)は3より大きいので、絶対値はそのまま外しました。
\[\lim_{x\to3-0}\frac{|x-3|}{x-3}=\lim_{x\to3-0}-\frac{x-3}{x-3}=-1\]
\(x\to3-0\)は左から極限を取ることを意味して、左極限と言います。\(x\)は3より小さいので、絶対値を外すにはマイナス符号が付きます。
積分に関する記号
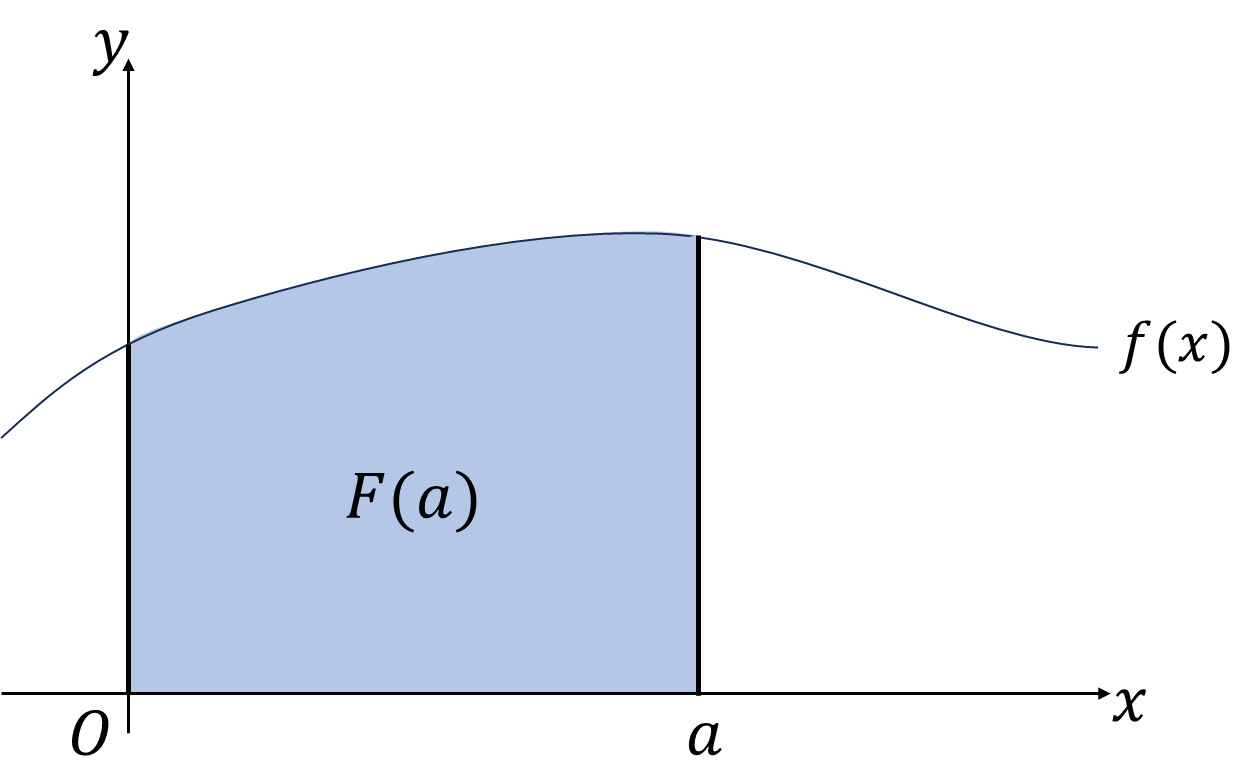
ある関数\(f(x)\)について、図の水色の部分(\(y=f(x),x=a,x\)軸,\(y\)軸で囲まれた部分)の面積\(F(a)\)とします。\(a\)を変数\(x\)におきかえたものを関数\(f(x)\)の原始関数\(F(x)\)と呼ぶことにします。関数\(f\)が負の値を取る区間では面積も負になります。
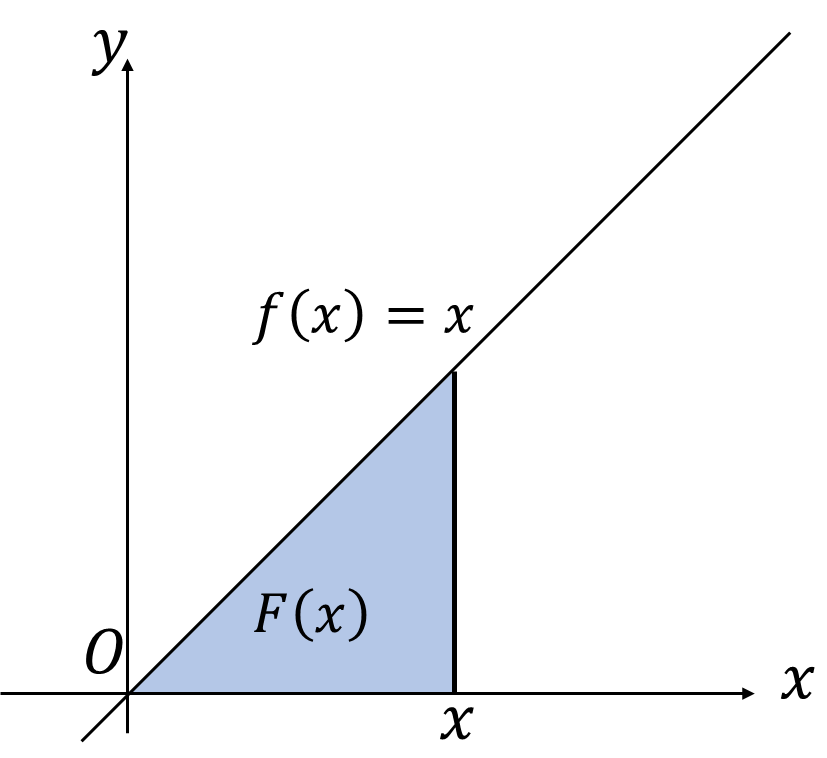
簡単な例として関数\(f(x)=x\)の原始関数は、図の直角三角形の面積なので、
\[F(x)=\frac{1}{2}\times底辺\times高さ=\frac{1}{2}x^2\]
です。

面積を表す記号としてこちらも便利です。
\[\int_a^bf(x)dx\]
この表記法は定積分と呼び、この表記1つで(\(y=f(x),x=a,x=b,x\)軸で囲まれた部分)、つまり水色の部分の面積を表します。\(y\)軸から\(x=b\)までの面積から、\(y\)軸から\(x=a\)までの面積を引いてると考えれば、先ほどの原始関数を使って
\[\int_a^bf(x)dx=F(b)-F(a)\]
とも表せます。
微分に関する記号
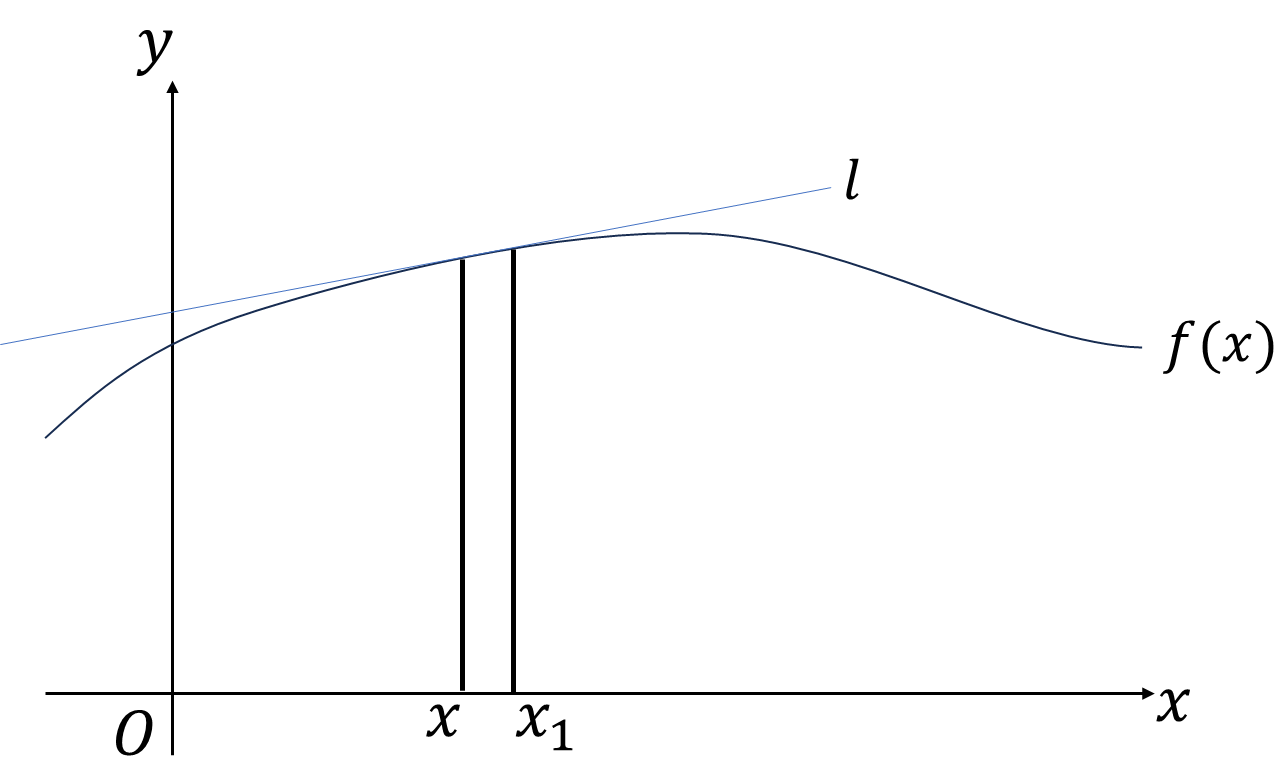
変数\(x\)が\(x_1\)に変化する状況で、変化量\(\varDelta x\)を、
\[\varDelta x:=x_1-x\]
と定義します。図の直線\(l\)は点\((x,f(x))\)と、点\((x_1,f(x_2))\)の2点を通る直線で、傾きは、
\[\frac{f(x_1)-f(x)}{x_1-x}=\frac{f(x+\varDelta x)-f(x)}{\varDelta x}\]
となりますね。更に微小量\(dx\)を
\[dx:=\lim_{x_1\to x}(x_1-x)=\lim_{\varDelta x\to 0}\varDelta x\]
と定義します。\(dx\)は変化量ですが、0に無限に近いものです。
微分を
\[\frac{df(x)}{dx}:=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)-f(x)}{\varDelta x}\]
と定義します。例えば\(f(x)=x^2\)であれば、
\[\frac{df(x)}{dx}=\lim_{\varDelta x\to0}\frac{(x+\varDelta x)^2-x^2}{\varDelta x}\]
\[=\lim_{\varDelta x\to0}\frac{x^2+2x\varDelta x+(\varDelta x)^2-x^2}{\varDelta x}=\lim_{\varDelta x\to0}(2x+\varDelta x)\]
\[\frac{df(x)}{dx}=2x\]
\(x^2\)の微分は\(2x\)となりますね。微分は
\[\frac{dy}{dx},\ \frac{d}{dx}y,\ \frac{df(x)}{dx},\ \frac{d}{dx}f(x),\ f'(x)\]
など様々な表記方法があります。
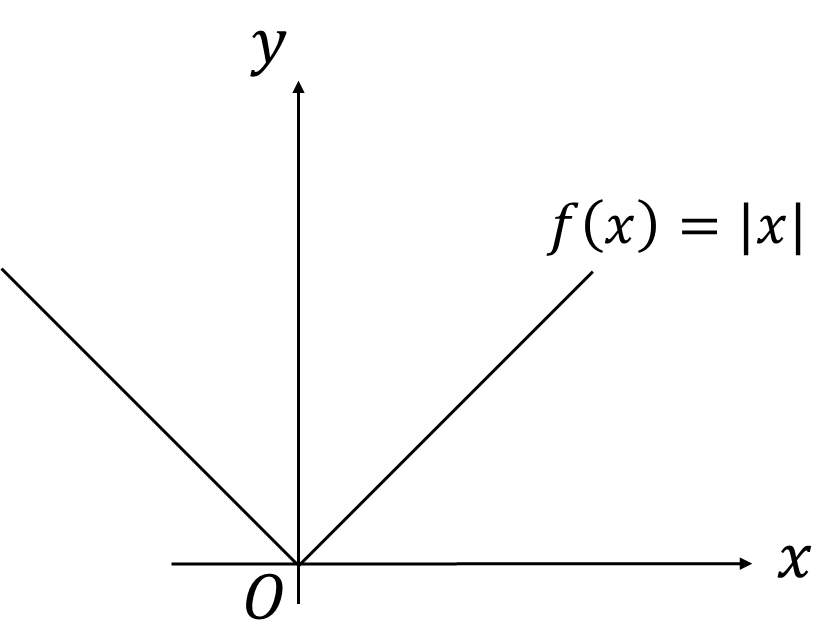
\(f(x)=|x|\)のような関数は注意して微分しなくてはなりません。
\[\frac{df(x)}{dx}=\lim_{\varDelta x\to0}\frac{|x+\varDelta x|-|x|}{\varDelta x}\]
\(x=0\)の時は、このように計算できません。左極限を取った場合は\(\varDelta x\)は負なので、
\[\lim_{\varDelta x\to-0}\frac{|0+\varDelta x|-|0|}{\varDelta x}=\lim_{\varDelta x\to-0}\frac{-\varDelta x}{\varDelta x}=-1\]
右極限の場合は、
\[\lim_{\varDelta x\to-0}\frac{|0+\varDelta x|-|0|}{\varDelta x}=\lim_{\varDelta x\to-0}\frac{\varDelta x}{\varDelta x}=1\]
\(df/dx\)の計算結果が1つに定まらずこのような点では微分不可能であると言います。微分を考えることができるのは滑らかなグラフだけで、折れたり切れているしているグラフでは微分できません。
微分積分学の基本定理
微分積分学の基本定理とは、簡単に言うと微分と積分が逆の操作であることを言います。
\[f(x)=\frac{d}{dx}\int_a^xf(x)dx\]
これを示していきます。
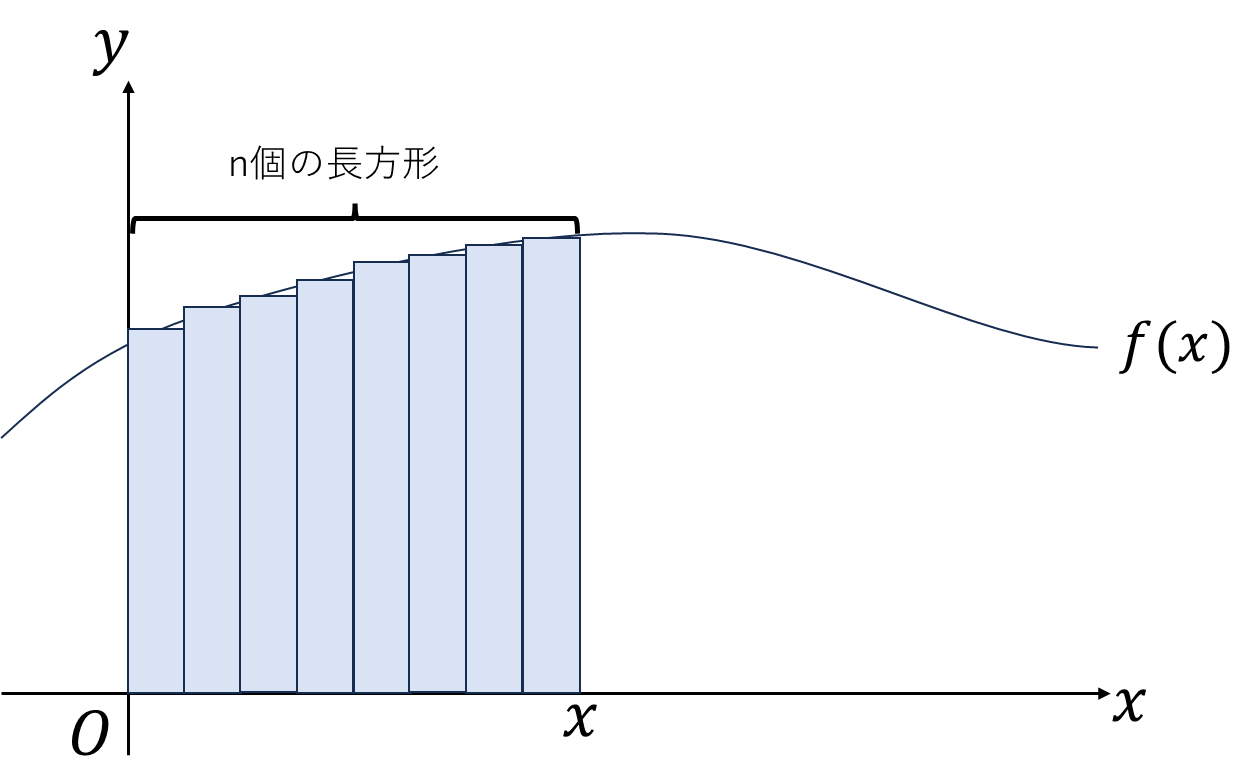
微分の記号のところでは具体的な計算方法を紹介しましたが積分の具体的な計算方法については説明していませんでした。積分は図のように長方形を足し合わせていくリーマン積分という方法がよく使われます。しかしこの長方形たちは適当に選ばれたわけでなく平均値の定理によって伸長を決められたエリート長方形です。

水色の部分の面積\(s\)は原始関数を使うことで、\(s=F(x_1)-F(x)\)となります。変化量\(\varDelta x=x_1-x\)を使うことで、\(s=F(x+\varDelta x)-F(x)\)とも表せますね。この面積\(s\)を関数\(f(x)\)を使って表す方法を考えます。
\[底辺\times高さ=\varDelta xf(x)\]
では小さいですね。
\[底辺\times高さ=\varDelta xf(x_1)=\varDelta xf(x+\varDelta x)\]
では大きすぎます。そこで、\(0\le c\le1\)となる定数\(c\)を使って、
\[s=f(x+c\varDelta x)\varDelta x\]
となる\(c\)が存在するのが直観的に分かると思います。これによって、
\[F(x+\varDelta x)-F(x)=f(x+c\varDelta x)\varDelta x\]
両辺を\(\varDelta x\)で割ると、
\[f(x+c\varDelta x)=\frac{F(x+\varDelta x)-F(x)}{\varDelta x}\]
両辺で\(\varDelta x\to0\)の極限を取ってみます。
\[\lim_{\varDelta x\to0}f(x+c\varDelta x)=\lim_{\varDelta x\to0}\frac{F(x+\varDelta x)-F(x)}{\varDelta x}\]
\[f(x)=\frac{dF(x)}{dx}\]
かなり近い所まで来ました。次に\(F(x)+C\ (Cは定数)\)でもこの式が成り立つことを見ていきます。
\[\frac{d}{dx}(F(x)+C)=\lim_{\varDelta x\to0}\frac{(F(x+\varDelta x)+C)-(F(x)+C)}{\varDelta x}\]
\[=\lim_{\varDelta x\to0}\frac{F(x+\varDelta x)-F(x)}{\varDelta x}=\frac{dF(x)}{dx}\]
そのため
\[f(x)=\frac{d}{dx}(F(x)+C)\]
定数\(C\)を\(-F(a)\)に置き換えます。\(C\)は定数なので、関数\(-F\)に定数\(a\)を入れた\(-F(a)\)も定数なのでこのようなことができます。
\[f(x)=\frac{d}{dx}(F(x)-F(a))\]
以上から、
\[f(x)=\frac{d}{dx}\int_a^xf(x)dx\]
微分積分額の基本定理が示せました。この等式は積分をしてから微分をするともとの関数に戻ることを意味しますが、今までの知識を使って微分してから積分をすると元の関数+定数になることも示せます。
\[f(x)=\frac{dF(x)}{dx}\]
の両辺を積分して、
\[\int_a^xf(x)dx=\int_a^x\frac{dF(x)}{dx}dx\]
\[F(x)-F(a)=\int_a^x\frac{dF(x)}{dx}dx\]
\[\int_a^x\frac{dF(x)}{dx}dx=F(x)-F(a)=F(x)+C\]
原始関数も任意の関数なので\(f(x)\)とすると、
\[\int_a^x\frac{df(x)}{dx}dx=f(x)+C\]
微分積分額の基本定理と見比べると
\[\frac{d}{dx}\int_a^xf(x)dx=f(x)\]
積分微分の順番ではもとの関数に戻りましたが、微分積分の順番では定数\(C\)が出てきましたね。微分と積分は厳密には逆の操作ではないようです。
積分を単に
\[\int f(x)dx=F(x)+C\]
と積分範囲を省略して書くこともあります。この記法を不定積分と言います。
積分の具体的な計算方法は、\(\varDelta x=(b-a)/n\)として、
\[\int_a^bf(x)dx\]
\[=f(a+c_1\varDelta x)\varDelta x+f(a+c_2\varDelta x)\varDelta x+\cdots+=f(a+c_n\varDelta x)\varDelta x\]
\[=\sum_{i=1}^nf(a+c_i\varDelta x)\varDelta x\]
ただし\(c_1,c_2,\cdots,c_n\)は定数となります。微分に比べてめんどくさそうですね。
微積分の線形性
最後に微分と積分の線形性(微積分の記号の分配法則、定数のくくりだし)だけ示しておきます。よく使いますので。関数\(f(x),g(x)\)、定数\(k\)について、
(i) 微分記号の分配
\[\frac{\{f(x+h)+g(x+h)\}-\{f(x)-g(x)\}}{h}\]
\[=\frac{f(x+h)-f(x)}{h}+\frac{g(x+h)-g(x)}{h}\]
両辺の極限を取って
\[\frac{d}{dx}(f+g)=\frac{d}{dx}f+\frac{d}{dx}g\]
(ii) 微分記号中の定数のくくりだし
\[k\frac{f(x+h)-f(x)}{h}=\frac{kf(x+h)-kf(x)}{h}\]
両辺の極限を取って
\[k\frac{d}{dx}f=\frac{d}{dx}(kf)\]
(iii) 積分記号の分配
\[\int_a^b\{f(x)+g(x)\}dx=\sum_{i=1}^n\{f(x+c_i\varDelta x)+g(x+b_i\varDelta x)\}\varDelta x\]
\[=\{f(x+c_1\varDelta x)+g(x+b_1\varDelta x)\}\varDelta x\]
\[+\{f(x+c_2\varDelta x)+g(x+b_2\varDelta x)\}\varDelta x\]
\[\cdots\]
\[+\{f(x+c_n\varDelta x)+g(x+b_n\varDelta x)\}\varDelta x\]
\[=f(x+c_1\varDelta x)\varDelta x+f(x+c_2\varDelta x)\varDelta x+\cdots+f(x+c_n\varDelta x)\varDelta x\]
\[+g(x+b_1\varDelta x)\varDelta x+g(x+b_2\varDelta x)\varDelta x+\cdots+g(x+b_n\varDelta x)\varDelta x\]
\[=\sum_{i=1}^nf(x+c_i\varDelta x)\varDelta x+\sum_{i=1}^ng(x+b_i\varDelta x)\varDelta x\]
以上から、
\[\int_a^b\{f(x)+g(x)\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx\]
(iv) 積分記号中の定数のくくりだし
\[\int_a^bkf(x)dx=\sum_{i=1}^nkf(x+c_i\varDelta x)\varDelta x\]
\[=kf(x+c_1\varDelta x)\varDelta x+kf(x+c_2\varDelta x)\varDelta x+\cdots+kf(x+c_n\varDelta x)\varDelta x\]
\[=k\{f(x+c_1\varDelta x)\varDelta x+f(x+c_2\varDelta x)\varDelta x+\cdots+f(x+c_n\varDelta x)\varDelta x\}\]
\[k\sum_{i=1}^nf(x+c_i\varDelta x)\varDelta x=k\int_a^bf(x)dx\]
以上から、
\[\int_a^bkf(x)dx=k\int_a^bf(x)dx\]
今回はここまでにします。