楽しい科学（理論）チャンネル

　今回は初等関数の微分や微分の便利な公式を見ていきます。

　合成関数の微分は簡単に示せます。\(f\)が\(x\)の関数で、さらに\(x\)が\(t\)の関数であるとき、 \[f=f(x)=f(x(t))\] \(f(x)\)は\(t\)の関数とみなせます。\(f\)の\(t\)微分は微分の定義より \[\frac{df}{dt}=\lim_{\varDelta t\to0}\frac{f(x(t+\varDelta t))-f(x(t))}{\varDelta t}\] \[=\lim_{\varDelta t\to0}\frac{f(x(t+\varDelta t))-f(x(t))}{x(t+\varDelta t)-x(t)}\frac{x(t+\varDelta t)-x(t)}{\varDelta t}\] \(\varDelta x=x(t+\varDelta t)-x(t)\)とすれば、\(\varDelta t\to0\)ならば\(\varDelta x\to0\)なので、 \[\frac{df}{dt}=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)-f(x)}{\varDelta x}\lim_{\varDelta t\to0}\frac{x(t+\varDelta t)-x(t)}{\varDelta t}\] 以上から合成関数\(f(x(t))\)について、 \[\frac{df}{dt}=\frac{df}{dx}\frac{dx}{dt}\] が成り立つ。

　対数関数\(y=\log_a x\)の微分を考えて意味ます。微分の定義に代入して \[\frac{d}{dx}\log_ax=\lim_{\varDelta x\to0}\frac{\log_a(x+\varDelta x)-\log_a x}{\varDelta x}\] \[=\lim_{\varDelta x\to0}\frac{\log_a(x+\varDelta x)-\log_a x}{\varDelta x}=\lim_{\varDelta x\to0}\frac{1}{x}\frac{x}{\varDelta x}\log_a\frac{x+\varDelta x}{x}\] \(x/\varDelta x=h\)とします。\(\varDelta x\to\infty\)の極限で\(h\to0\)となるので、 \[\frac{d}{dx}\log_ax=\lim_{h\to\infty}\frac{1}{x}h\log_a\left(1+\frac{1}{h}\right)=\lim_{h\to\infty}\frac{1}{x}\log_a\left(1+\frac{1}{h}\right)^h\] ネイピア数\(e\)を \[e:=\lim_{h\to\infty}\left(1+\frac{1}{h}\right)^h\] このように定義します。\(e\simeq2.7\)と知られています。この近似値は覚えておきましょう。ネイピア数を使えば対数の微分は \[\frac{d}{dx}\log_ax=\frac{1}{x}\log_ae\] 特に対数の底が\(e\)の時は、 \[\frac{d}{dx}\log_ex=\lim_{h\to0}\frac{1}{x}\log_ee=\frac{1}{x}\] 底が\(e\)の時の対数を特に\(\log_e=\ln\)と表記されます。対数の微分は、 \[\frac{d}{dx}\log_ax=\frac{\log_ae}{x}\] とくに自然対数\(\ln x\)の微分は \[\frac{d}{dx}\ln x=\frac{1}{x}\] となります。

　定数\(\alpha\)について、\(y=x^\alpha\)とします。べき関数の自然対数を取ります。 \[\ln x^\alpha=\alpha\ln x\] 両辺を\(x\)で微分します。左辺は合成関数の微分を使います。 \[\frac{d(\ln x^\alpha)}{d(x^\alpha)}\frac{d(x^\alpha)}{dx}=\alpha\frac{d(\ln x)}{dx}\] \[\frac{1}{x^\alpha}\frac{d(x^\alpha)}{dx}=\alpha\frac{1}{x}\] 両辺を\(x^\alpha\)倍して、 \[\frac{d}{dx}x^\alpha=\alpha x^{\alpha-1}\]

　\(a\ge0\)として、\(y=a^x\)の微分を考えます。指数関数の自然対数を取ります。 \[\ln a^x=x\ln a\] 両辺を\(x\)で微分します。 \[\frac{d(\ln a^x)}{d(a^x)}\frac{d a^x}{dx}=\ln a\] \[\frac{1}{a^x}\frac{d a^x}{dx}=\ln a\] 両辺を\(a^x\)倍して \[\frac{d}{dx}a^x=\ln a\times a^x\] とくに指数関数の底がネイピア数の場合は、 \[\frac{d}{dx}e^x=\ln e\times e^x=e^x\] 微分しても同じ関数\(e^x\)になりますね。

　微分積分額の基本定理より \[\int\frac{df(x)}{dx}dx=f(x)+C\] 対数関数\(\ln x\)、べき関数\(x^\alpha\)、指数関数\(e^x\)を代入すると、 \[\int \frac{1}{x}dx=\ln x+C\] \[\int\alpha x^{\alpha-1}dx=x^\alpha+C\ (\alpha\neq-1)\] \[\int e^xdx=e^x+C\] これらも覚えなくてもいいですが、微分の逆算になりますので、パッと思い出せるようにしましょう。例として、\(f(x)=(x+3)^7\)の積分を見てみましょう。 \[\frac{d}{dx}\left(\frac{1}{8}(x+3)^8\right)=\frac{1}{8}\frac{d(x+3)^8}{d(x+3)}\frac{d(x+3)}{dx}\] \[=\frac{1}{8}\times8(x+3)^7\times1=f(x)\] なので、 \[\int f(x)dx=\frac{1}{8}(x+3)^8+C\] となります。この積分方法はテイラーの定理を示すのに使うので理解しましょう。

　テイラーの定理は、平均値の定理の拡張です。テイラーの定理を平均値の定理を使って示していきましょう。

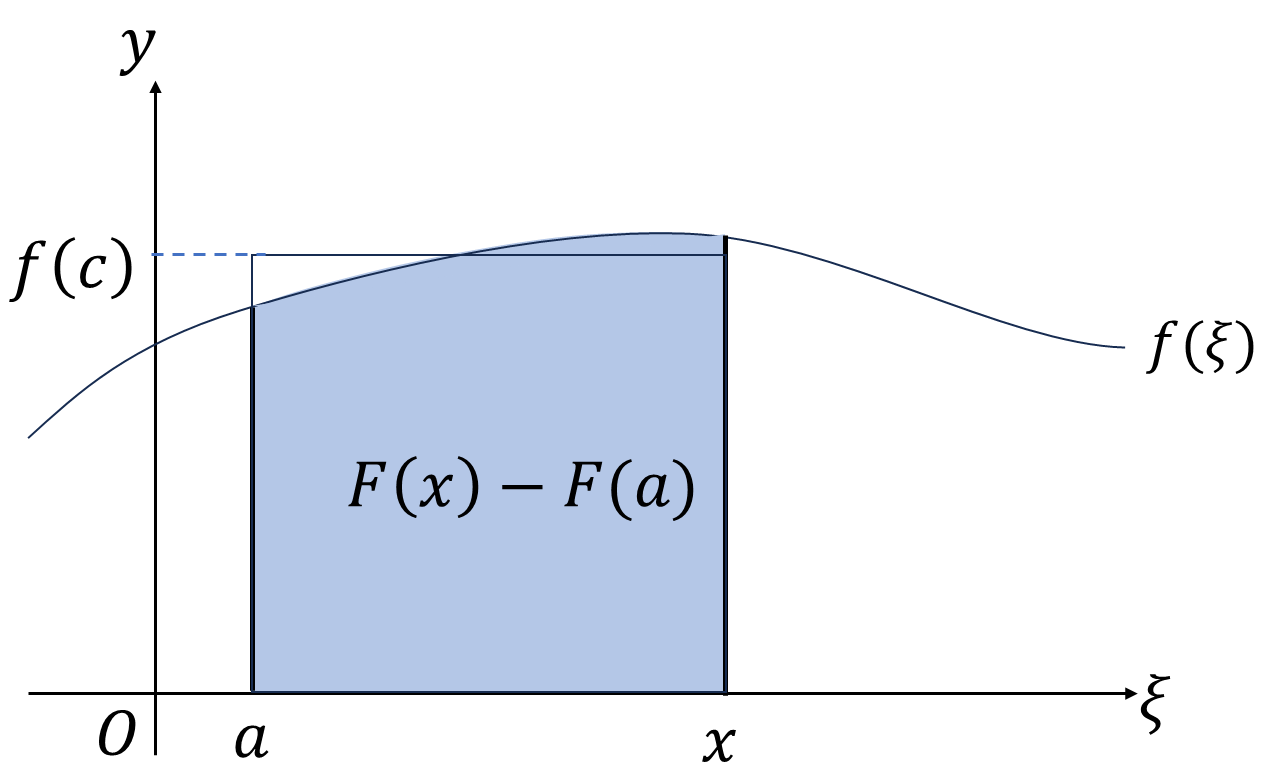
　図の水色の部分の面積は原始関数を使って、\(F(a)-F(x)\)また関数\(f(x)\)を用いて、 \[F(x)-F(a)=f(c)(x-a)\] \[F(x)=F(a)+f(c)(x-a)\] となる\(a\)と\(x\)の間の数\(c\)が存在するというのが平均値の定理の主張です。原始関数\(F(x)\)は任意の関数なので、 \[F(x)\to f(x)\] と置き換えます。そうすると\(f(x)\)も置き換えが必要ですね。 \[f(x)\to \frac{df(x)}{dx}\] になります。 \[f(x)=f(a)+\frac{df(c)}{dx}(x-a)\] ではこの等式の両辺を\(a\)から\(x\)の範囲で積分しましょう。積分範囲と積分変数で記号が被らないように適当な変数\(\xi\)を使います。 \[\int_a^xf(\xi)d\xi=f(a)\int_a^xd\xi+\frac{df(c)}{dx}\int_a^x(\xi-a)d\xi\] \[F(x)-F(a)=f(a)(x-a)+\frac{df(c)}{dx}\frac{(x-a)^2}{2}\] \[F(x)=F(a)+f(a)(x-a)+\frac{df(c)}{dx}\frac{(x-a)^2}{2}\] \(f(a),df/dx(c)\)は定数なので積分の外に出してあります。原始関数\(F(x)\)は任意の関数なので、 \[F(x)\to f(x)\] と置き換えます。そうすると、 \[f(x)\to \frac{df(x)}{dx}\] \[\frac{df(x)}{dx}\to \frac{d^2f(x)}{dx^2}\] とする必要がありますね。\(d^2f(x)/dx^2\)は\(f(x)\)を２階微分したものです。 \[f(x)=f(a)+\frac{df(a)}{dx}(x-a)+\frac{d^2f(c)}{dx^2}\frac{(x-a)^2}{2}\] もう規則性に気付いたと思いますがもう1回だけこの等式の両辺を積分してみます。 \[\int_a^x f(\xi)d\xi=\int_a^x\left(f(a)+\frac{df(a)}{dx}(\xi-a)+\frac{d^2f(c)}{dx^2}\frac{(\xi-a)^2}{2}\right)d\xi\] \[F(x)-F(a)=f(a)(x-a)+\frac{df(a)}{dx}\frac{(x-a)^2}{2}+\frac{d^2f(c)}{dx^2}\frac{(x-a)^3}{2\times3}\] またまた原始関数を置き換えます。 \[F(x)\to f(x)\] \[f(x)\to \frac{df}{dx}(x)\] \[\frac{d^nf(x)}{dx^n}\to \frac{d^{(n+1)}f(x)}{dx^{(n+1)}}\ \ (n\ge1)\] となります。 \[f(x)=f(a)+\frac{df(a)}{dx}(x-a)\] \[+\frac{d^2f(a)}{dx^2}\frac{(x-a)^2}{2}+\frac{d^3f(c)}{dx^3}\frac{(x-a)^3}{2\times3}\] 更に階乗 \[0!=1\] \[1!=1\] \[2!=2\times1\] \[3!=3\times2\times1\] と０階微分(微分の操作を０回するつまり操作しない) \[\frac{d^0}{dx^0}f(x):=f(x)\] を定義することで、 \[f(x)=\frac{d^0f(a)}{dx^0}\frac{(x-a)^0}{0!}+\frac{d^1f(a)}{dx^1}\frac{(x-a)^1}{1!}\] \[+\frac{d^2f(a)}{dx^2}\frac{(x-a)^2}{2!}+\frac{d^3f(c)}{dx^3}\frac{(x-a)^3}{3!}\] 総和の記号を使うと、 \[f(x)=\sum_{k=0}^{2}\frac{1}{k!}\frac{d^kf(a)}{dx^k}(x-a)^k+\frac{1}{n!}\frac{d^3f(c)}{dx^3}(x-a)^3\] 今は積分原始関数の置き換えを３回やりましたが\(n\)回やると、 \[f(x)=\sum_{k=0}^{n-1}\frac{1}{k!}\frac{d^kf(a)}{dx^k}(x-a)^k+\frac{1}{n!}\frac{d^nf(c)}{dx^n}(x-a)^n\] となりそうですね。これがテイラーの定理です。