楽しい科学（理論）チャンネル

　今回は初等関数の微分や微分の便利な公式を見ていく会のパート２です。

三角関数の微分を証明するために少し準備をします。

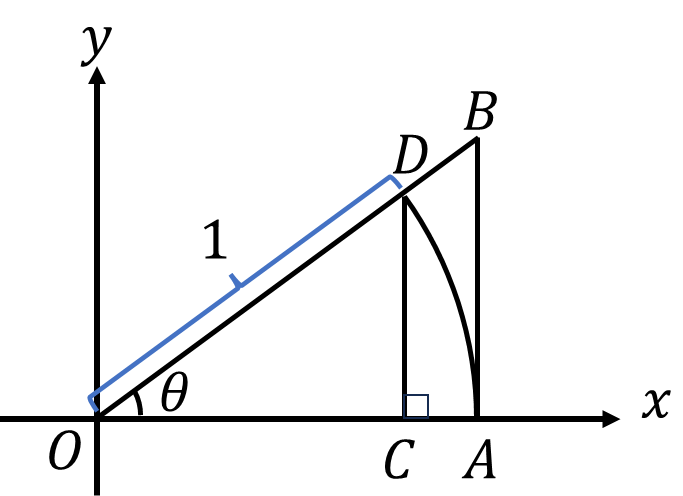
　こちらの図は、半径１、角度\(\theta\)の扇形に補助線を引いた図です。この図から、 \[三角形CODの面積\lt扇形AODの面積\lt三角形AOBの面積\tag{1}\] だとわかります。弧度法に依る三角比を使って、 \[三角形CODの面積=\frac{1}{2}\times OC\times CD=\frac{1}{2}\cos\theta\sin\theta\] \[扇形AODの面積=\frac{\theta}{2\pi}\times\pi\times1^2=\frac{\theta}{2}\] \(AB=OB\sin\theta\)、\(OB\cos\theta=OA=1\)より \[三角形AOBの面積=\frac{1}{2}\times OA\times AB=\frac{1}{2}OB\sin\theta=\frac{\sin\theta}{2\cos\theta}\] 以上から不等式(1)は \[\frac{1}{2}\cos\theta\sin\theta\lt\frac{\theta}{2}\lt\frac{\sin\theta}{2\cos\theta}\] となります。この不等式に\(2/\sin\theta\)を掛け、逆数をとります。 \[\cos\theta\lt\frac{\sin\theta}{\theta}\lt\frac{1}{\cos\theta}\] この不等式は\(0\lt\theta\lt\pi/2\)で常に成り立ちます。さらに\(\theta\to0\)の極限で、 \[\cos\theta\to1\] \[\frac{1}{\cos\theta}\to1\] 不等式の両端の極限はどちらも1に収束するため、間の\(\sin\theta/\theta\)も１に収束することが直観的に分かるでしょう。 \[\lim_{\theta\to0}\frac{\sin\theta}{\theta}=1\] これを利用して、以下の極限も計算できます。 \[\lim_{\theta\to0}\frac{1-\cos\theta}{\theta}=\lim_{\theta\to0}\frac{1-\cos^2\theta}{\theta(1+\cos\theta)}=\lim_{\theta\to0}\frac{\sin\theta}{\theta}\frac{1}{1+\cos\theta}\sin\theta\] \[=1\times\frac{1}{2}\times 0=0\] \[\lim_{\theta\to0}\frac{1-\cos\theta}{\theta}=0\] これも三角関数の微分に使います。

　まずは\(\cos x\)の微分を求めましょう。 \[\frac{d}{dx}\cos x=\lim_{\varDelta x\to0}\frac{\cos(x+\varDelta x)-\cos x}{\varDelta x}\] 加法定理を使います。 \[=\lim_{\varDelta x\to0}\frac{1}{\varDelta x}(\cos x\cos \varDelta x-\sin x\sin \varDelta x-\cos x)\] \[=-\cos x\lim_{\varDelta x\to0}\frac{1-\cos\varDelta x}{\varDelta x}-\sin x\lim_{\varDelta x\to0}\frac{\sin\varDelta}{\varDelta x}\] さっき示した極限を利用すれば \[\frac{d}{dx}\cos x=-\sin\theta\] と分かりますね。次は\(\sin x\)の微分を求めましょう。 \[\frac{d}{dx}\sin x=\lim_{\varDelta x\to0}\frac{\sin(x+\varDelta x)-\sin x}{\varDelta x}\] 加法定理を使います。 \[=\lim_{\varDelta x\to0}\frac{1}{\varDelta x}(\sin x\cos\varDelta x+\cos x\sin\varDelta x-\sin x)\] \[=-\sin x\lim_{\varDelta x\to0}\frac{1-\cos\varDelta x}{\varDelta x}+\cos x\lim_{\varDelta x\to0}\frac{\sin\varDelta x}{\varDelta x}\] こちらも極限を取ることで、 \[\frac{d}{dx}\sin x=\cos x\] これで\(\sin x,\cos x\)の微分を示すことができましたね。

　関数\(f(x),g(x)\)の積の微分を考えてみましょう。定義通り計算します。 \[\frac{d}{dx}\{f(x)g(x)\}=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)g(x+\varDelta x)-f(x)g(x)}{\varDelta x}\] 分子に\(f(x+)g(x+\varDelta x)-f(x)g(x+\varDelta x)\)を足します。０なので一見意味がないようですが、 \[=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)g(x+\varDelta x)-f(x)g(x+\varDelta x)}{\varDelta x}\] \[+\lim_{\varDelta x\to0}\frac{f(x)g(x+\varDelta x)-f(x)g(x)}{\varDelta x}\] \[=\lim_{\varDelta x\to0}\frac{f(x+\varDelta x)-f(x)}{\varDelta x}g(x+\varDelta x)\] \[+\lim_{\varDelta x\to0}f(x)\frac{g(x+\varDelta x)-g(x)}{\varDelta x}\] 上手いこと２つの微分に分けることができました。 \[\frac{d}{dx}\{f(x)g(x)\}=\frac{df(x)}{dx}g(x)+f(x)\frac{dg(x)}{dx}\] これは積の微分という公式です。これを活用することで\(\tan x\)を微分することができます。 \[\frac{d}{dx}\tan x=\frac{1}{\cos x}\frac{d}{dx}\sin x+\sin x\frac{d}{dx}\frac{1}{\cos x}\] 合成関数の微分も使います。 \[=1+\sin x\frac{d}{d(\cos x)}\left(\frac{1}{\cos x}\right)\frac{d\cos x}{dx}\] \[=1+\sin x\frac{-1}{\cos^2 x}(-\sin x)=1+\tan^2 x\]

　前回テイラーの定理というものを導出しました。 \[f(x)=\sum_{k=0}^{n-1}\frac{1}{k!}\frac{d^kf(a)}{dx^k}(x-a)^k+\frac{1}{n!}\frac{d^nf(c)}{dx^n}(x-a)^n\] \(c\)は\(a\)と\(x\)の間の数です。\(f(x)\)が無限に微分可能で、余剰項の極限が０に収束する \[\lim_{n\to\infty}\frac{1}{n!}\frac{d^nf(a)}{dx^n}(x-a)^n=0\] 場合に関数\(f(x)\)を \[f(x)=\sum_{n=0}^\infty\frac{1}{n!}\frac{d^nf(a)}{dx^n}(x-a)^n\] 無限級数で表すことができます。この展開方法をテイラー展開と言います。特に\(a=0\)の時 \[f(x)=\sum_{n=0}^\infty\frac{1}{n!}\frac{d^nf(0)}{dx^n}x^n\] これをマクローリン展開と言います。この展開が成り立つにも余剰項が０に収束することを示さなければなりません。直観的な説明になってしまいますが、階乗と、べき乗では階乗の方がより早く大きくなります。 \[\lim_{n\to\infty}\frac{3^n}{n!}=\lim_{n\to\infty}\frac{3\cdot3\cdot3\cdot3\cdots3}{1\cdot2\cdot3\cdot4\cdots n}=0\] 3のべき乗を例に取ると、分子はずっと３を掛けていますが、階乗は３以降は４、５、６とずっと３より大きい数字を掛け続けるため、いずれ０に収束します。３でない任意の数のべき乗でもいずれ階乗に抜かされます。そのためすくなくとも\(d^nf(0)/dx^n\)が\(n\)に対して増加し続けない関数であればマクローリン展開できます。

　オイラーの公式を示すため、\(\sin x,\cos x,e^x\)の３つの関数をテイラー展開してみます。まずは\(y(x)=\sin x\)です。\(n\)階微分を\(y^{(n)}(x)\)と表すことにすると、 \[y^{(0)}(x)=\sin x,\ y^{(0)}(0)=0\] \[y^{(1)}(x)=\cos x,\ y^{(1)}(0)=1\] \[y^{(2)}(x)=-\sin x,\ y^{(2)}(0)=0\] \[y^{(3)}(x)=-\cos x,\ y^{(3)}(0)=-1\] \[y^{(4)}(x)=\sin x,\ y^{(4)}(0)=0\] \[y^{(5)}(x)=\cos x,\ y^{(5)}(0)=1\] \[y^{(6)}(x)=-\sin x,\ y^{(6)}(0)=0\] \[y^{(7)}(x)=-\cos x,\ y^{(7)}(0)=-1\] となります。\(y^{(n)}\)は\(n\)の増加に対して増加することはないので、\(\sin x\)のマクローリン展開は \[\sin x=\sum_{n=0}^{\infty}\frac{y^{(n)}(0)}{n!}x^n=\frac{1}{1!}x^1+\frac{-1}{3!}x^3+\frac{1}{5!}x^5+\frac{-1}{7!}x^7+\cdots\] \[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\] と表せますね。次に\(y(x)=\cos x\)をマクローリン展開していきます。\(\cos x\)の微分は \[y^{(0)}(x)=\cos x,\ y^{(0)}(0)=1\] \[y^{(1)}(x)=-\sin x,\ y^{(1)}(0)=0\] \[y^{(2)}(x)=-\cos x,\ y^{(2)}(0)=-1\] \[y^{(3)}(x)=\sin x,\ y^{(3)}(0)=0\] \[y^{(4)}(x)=\cos x,\ y^{(4)}(0)=1\] \[y^{(5)}(x)=-\sin x,\ y^{(5)}(0)=0\] \[y^{(6)}(x)=-\cos x,\ y^{(6)}(0)=-1\] ですので、 \[\cos x=\sum_{n=0}^{\infty}\frac{y^{(n)}(0)}{n!}x^n=\frac{1}{0!}x^0+\frac{-1}{2!}x^2+\frac{1}{4!}x^4+\frac{-1}{6!}x^6+\cdots\] \[\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\] これが\(\cos x\)のマクローリン展開ですね。次に\(y=e^x\)のマクローリン展開を見ていきます。\(e^x\)は何階微分しても\(e^x\)なので、 \[y^{(n)}(x)=e^x,\ y^{(n)}(0)=e^0=1\] となります。以上から、マクローリン展開は \[e^x=\frac{1}{0!}x^0+\frac{1}{1!}x^1+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\frac{1}{5!}x^5+\cdots\] \[e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\frac{x^6}{6!}+\frac{x^7}{7!}+\cdots\] これが\(e^x\)のマクローリン展開です。この式\(x\)を\(ix\)に置き換えてみましょう。\(i\)は虚数単位\(i:=\sqrt{-1}\)です。 \[e^{ix}=1+\frac{ix}{1!}-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+\frac{ix^5}{5!}-\frac{x^6}{6!}-\frac{ix^7}{7!}+\cdots\] \(e^{ix}\)のマクローリン展開を実部と虚部に分けます。 \[e^{ix}=\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)\] \[+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\right)\] なんと\(\cos x,\ \sin x\)のマクローリン展開が出てきましたね。 \[e^{ix}=\cos x+i\sin x\] この等式がオイラーの公式です。微分方程式を解くときにも使いますし、量子力学でも使います。いろいろなところで使います。