楽しい科学（理論）チャンネル

　まずは帯電について、皆さんはドアノブなどに触れたときに静電気でビリっとなったことはないだろうか。これは自分の手が＋電気を帯びていて、ドアノブ触れようとしたときにドアノブから－の電荷をもつ電子が手に放電されるためにおこる。金属は電子がある程度自由に動くことができるため静電気が起こりやすい。

　また帯電した下敷きに浮く、帯電したビニールひもを見たことがあるだろうか。ビニールひもや下敷きは－の電気を帯びやすい同じ符号の電気を帯びた物体どうしは反発する力がはたらく。この記事では電気を帯びている物体を電荷と呼ぶことにする。電荷の帯びている電気の大きさにも大小関係がほしい。そこで電気量というものを定義する。

＊＊電気量の定義 ＊＊

電子１個の電気量の大きさを \[e=1.602\ 176\ 634\times10^{-19}\mathrm{\ C}\] と定義する。

　電気量の単位を\(\mathrm{C}\)をクーロンと呼ぶ。電子は負の電荷なので、電子を\(\frac{1}{1.602\ 176\ 634\times10^{-19}}\)個集めたときの電荷量が\(-1\mathrm{\ C}\)ともいえる。\(\mathrm{C}\)は基本SI単位アンペア\(\mathrm{A}\)を使い\(\mathrm{C=A\ s^{-1}}\)とあらわす。アンペアについては後で解説しよう。

　原点\(O\)に、電気量\(Q\)の電荷を貼り付ける。位置\(\boldsymbol{r}\)にある電気量\(q\)の電荷が受ける力をクーロン力という。

＊＊クーロンの法則＊＊

　原点にある電気量\(Q\)の電荷から位置\(\boldsymbol{r}\)にある電気量\(q\)の電荷が受ける力は、 \[\boldsymbol{F}(\boldsymbol{r}):=k\frac{qQ}{r^2}\hat{\boldsymbol{r}}\] 　と表せる。

　\(k\)はクーロン定数という。クーロン係数の単位を求めよう。\(\mathrm{N}=[k]\mathrm{C^2\cdot m^{-2}}\)であるから、クーロン係数の単位は\(\mathrm{N\ m^2\ C^{-2}}\)SI基本単位を用いると、\(\mathrm{kg\ m^3\ s^{-4}\ A^{-2}}\)である。電荷\(q,Q\)の符号が同じ場合斥力になり、符号が異なる場合は引力になる。磁石同士にも距離の２乗に反比例する力がはたらく。同じ極同士の磁石を近づけると、斥力がはたらき、逆の極同士の磁石を近づけると引力がはたらく。

　力学では物体同士が相互作用を与えあうという考え方が強い。電磁気学では、電荷が固定された実験装置から受ける相互作用をみるというシチュエーションが多いそのため、電磁気の式も実験装置が作る場が電荷にどう影響するかみたいな書き方がされる。 \[\boldsymbol{E}(\boldsymbol{r}):=\frac{\boldsymbol{F}(\boldsymbol{r})}{q}\] 　電場を、装置が位置\(\boldsymbol{r}\)にある電荷\(1\ C\)に及ぼす力としよう。例えば原点\(O\)に電荷\(Q\)を発生させる装置が作る電場\(\boldsymbol{E}(\boldsymbol{r})\)は、 \[\boldsymbol{E}(\boldsymbol{r})=\frac{kQ}{r^2}\hat{\boldsymbol{r}}\] である。電場\(\boldsymbol{E}(\boldsymbol{r})\)が時間的に変化する場合は\(\boldsymbol{E}(\boldsymbol{r},t)\)と表示されることもある。電場の単位は\(\mathrm{N\ C^{-1}}\)である。SI単位系で表すと、\(\mathrm{kg\ m\ s^{-3}\ A^{-1}}\)である。

次に電位を定義する。 \[V(\boldsymbol{r}):=\int_{\boldsymbol{r_0}}^{\boldsymbol{r}}-\boldsymbol{E}(\boldsymbol{r})\cdot d\boldsymbol{r}+V(\boldsymbol{r_0})\] 　電位の単位は\(\mathrm{V}\)ボルトである。SI基本単位系を用いると、\(\mathrm{kg\ m^2\ s^{-3}\ A^{-1}}\)である。このように電場\(\boldsymbol{E}\)をスカラーとして扱うことで、力学でエネルギー系から問題を解くようなことができる。\(q\boldsymbol{E}\)が保存力の場合\(mv^2/2+qV(\boldsymbol{r})=const.\)も使える。

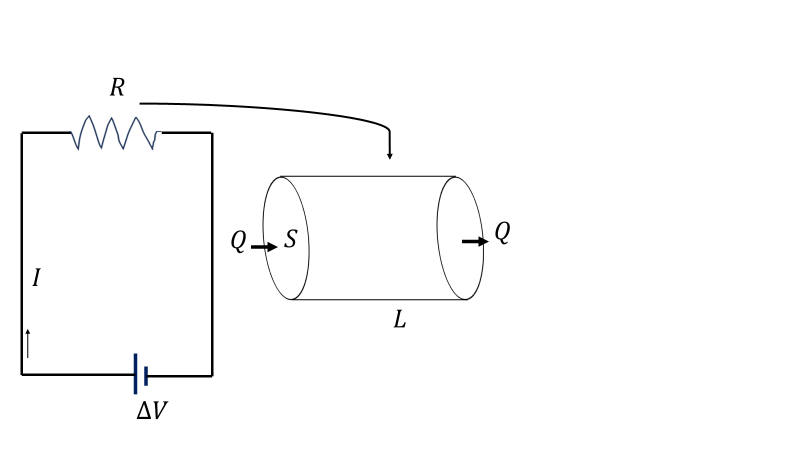
　図のような実験装置を考える。\(\varDelta V\)で表記されている装置を直流電源と呼ぶことにする。電源装置の記号の長い線のほう(+極)から電荷が放出され、短い線のほう(-極)から電荷が入るというルールになっている。電気回路に常に一定電気量を供給してくれる理想の装置である。ただの電池と思ってもらっていい。実際の電池も直流電源であるが、電池内部の電気の元となるイオンが低下すると若干の減衰がある。\(R\)ギザギザの装置を電気抵抗器という。電気抵抗器はギザギザのマークがよく利用される。右の図は電気抵抗器をちゃんと書いたものである。

　電圧\(\varDelta V\)は電位の差のことである。+極の電位を\(V_A\)、－極の電位を\(V_B\)とすると、\(\varDelta V=V_A-V_B\)で表すことができる。電気抵抗器\(R\)に流れる電流を\(I\)次のように定義する。

\[I:=\frac{dQ}{dt}\] \(Q\)は抵抗器に入ってくる電気量で電流の単位は\(\mathrm{C\ s^{-1}}\)である。基本単位系を使うと\(\mathrm{A}\)アンペアである。今回は回路の分岐が無いのでどこのケーブル、装置でも１秒間辺りに移動する電荷の量が同じである。しかし、電流は常に向きがあるにも関わらず、電流\(I\)はスカラーであるため物理量として十分でないことがある。 \[I(\boldsymbol{r}):=\iint_{S}\boldsymbol{j}(\boldsymbol{r})\cdot d\boldsymbol{S}\] で定義される電流密度\(\boldsymbol{j}(\boldsymbol{r})\)が基本方程式に利用しやすい。電流密度の方向は電流が流れている方向である。電流密度の単位は\(\mathrm{A\ m^{-2}}\)である。 電気抵抗器の記号に\(R\)を用いたがこれはオームの法則に従う電気抵抗である。

＊＊オームの法則＊＊

物質に流れる電流\(I\)は物質に加えられる電圧\(\varDelta V\)に比例する。その比例係数を電気抵抗\(R\)と呼ぶ。 \[\varDelta V=RI\]

電気抵抗の単位は\(\mathrm{V/A=\Omega}\)オームである。SI基本単位系では\(\mathrm{kg\ m^2\ s^{-3}\ A^{-2}}\)である。SI基本単位\(\mathrm{A}\)についての説明は終わり。

　磁石同士にも力がはたらく。N極を(＋)、S極を(-)の磁荷\(m\)を持つものとする。N極だけ、S極だけの磁荷は見つかっていない。(棒磁石を半分に割ると2つのS極N極を持つ磁石になってしまうのだ。)電気に対して磁気の式が理解しずらいのは磁荷がない為だと僕は思う。というわけで始めに磁荷を使って磁気の式を導いて最後に磁荷を消し去る。というわけでこれからの話は嘘である。とはいえ、磁石が受ける力を考えるときには有効な話ではある。磁荷を仮定することで電荷のと同じ式で磁荷が扱える。

＊＊クーロンの法則(磁力)＊＊

　原点にある磁気量\(M\)の磁荷から位置\(\boldsymbol{r}\)にある磁気量\(m\)の磁荷が受ける力は、 \[\boldsymbol{F}_m(\boldsymbol{r}):=k_m\frac{mM}{r^2}\hat{\boldsymbol{r}}\] 　である。

　磁荷の単位は\(\mathrm{Wb}\)ウェーバーである。\(k_m\)は磁気のクーロン係数で単位は\(\mathrm{N\ m^2\ Wb^{-2}}\)である。こちらも点とみなせる磁荷\(M\)がつくる磁場\(\boldsymbol{H}(\boldsymbol{r})\)を \[\boldsymbol{H}(\boldsymbol{r}):=k_m\frac{M}{r^2}\hat{\boldsymbol{r}}\] と定義して、磁気量\(M\)の磁荷が受ける力を\(\boldsymbol{F}_m(\boldsymbol{r})=m\boldsymbol{H}(\boldsymbol{r})\)と表せるようにする。磁場の単位は\(\mathrm{N\ Wb^{-1}}\)である。運動している電荷は磁場から力がはたらくことが知られている。磁束密度\(\boldsymbol{B}:=\mu_0\boldsymbol{H}\)というものを定義する。\(\mu_0\)は比例係数。

＊＊ローレンツ力＊＊

　電荷\(q\)が速度\(\boldsymbol{v}\)で運動している場合、磁束密度\(\boldsymbol{B}\)から受ける力は \[\boldsymbol{F}_M=q\boldsymbol{v}\times\boldsymbol{B}\] 　である。

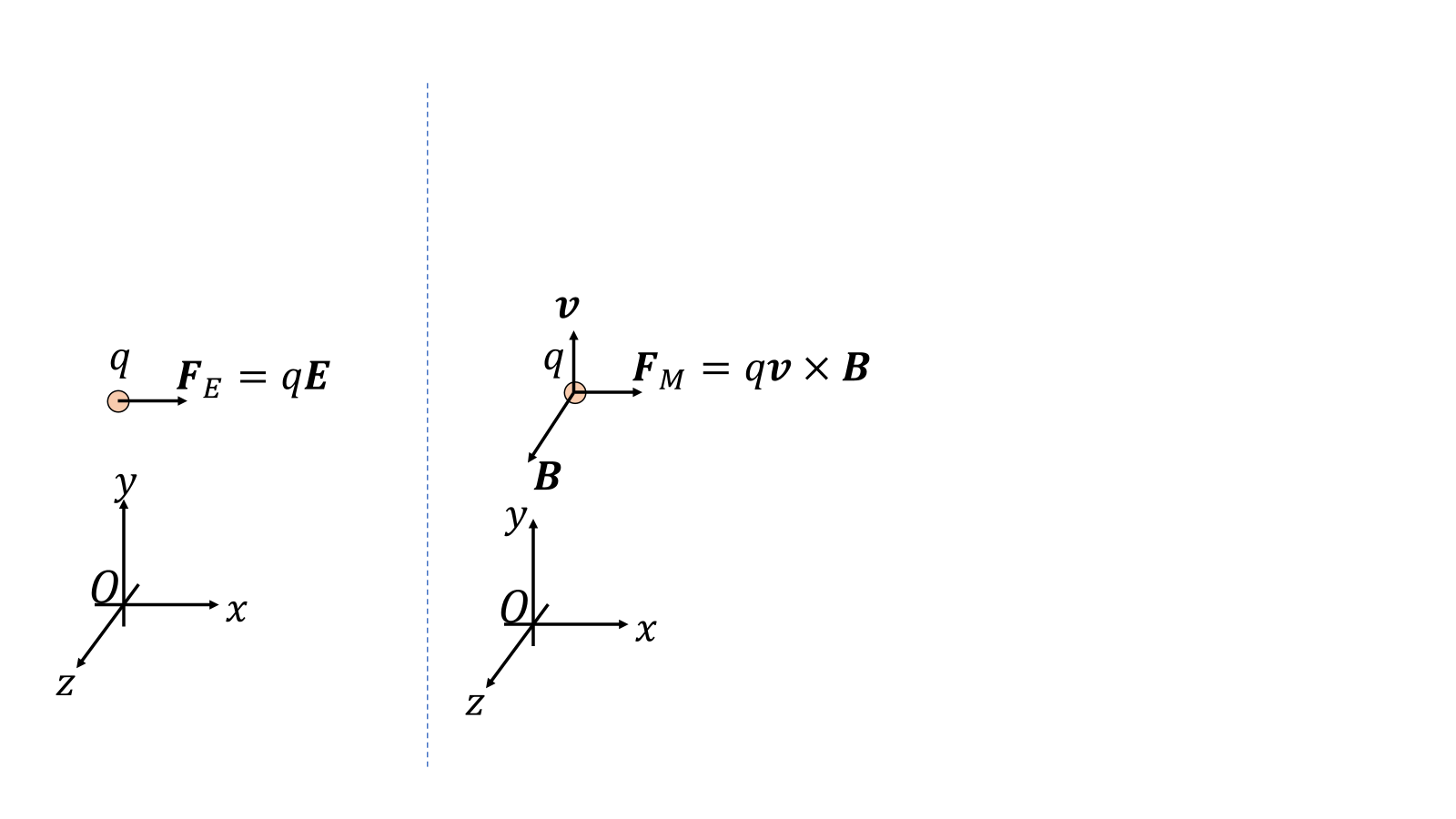
電荷が電場から受ける力の向きは電場と同じ方向であるが、磁場(磁束密度)から受ける力は速度と磁束密度の右ねじ方向である。電荷の速度が0の時には、電荷には磁場からの力\(\boldsymbol{F}_M\)は生じない。一般に電荷が磁場、電場から受ける力を \[\boldsymbol{F}=\boldsymbol{F}_E+\boldsymbol{F}_M\] \[\boldsymbol{F}=q\boldsymbol{E}+q\boldsymbol{v}\times\boldsymbol{B}\] である。

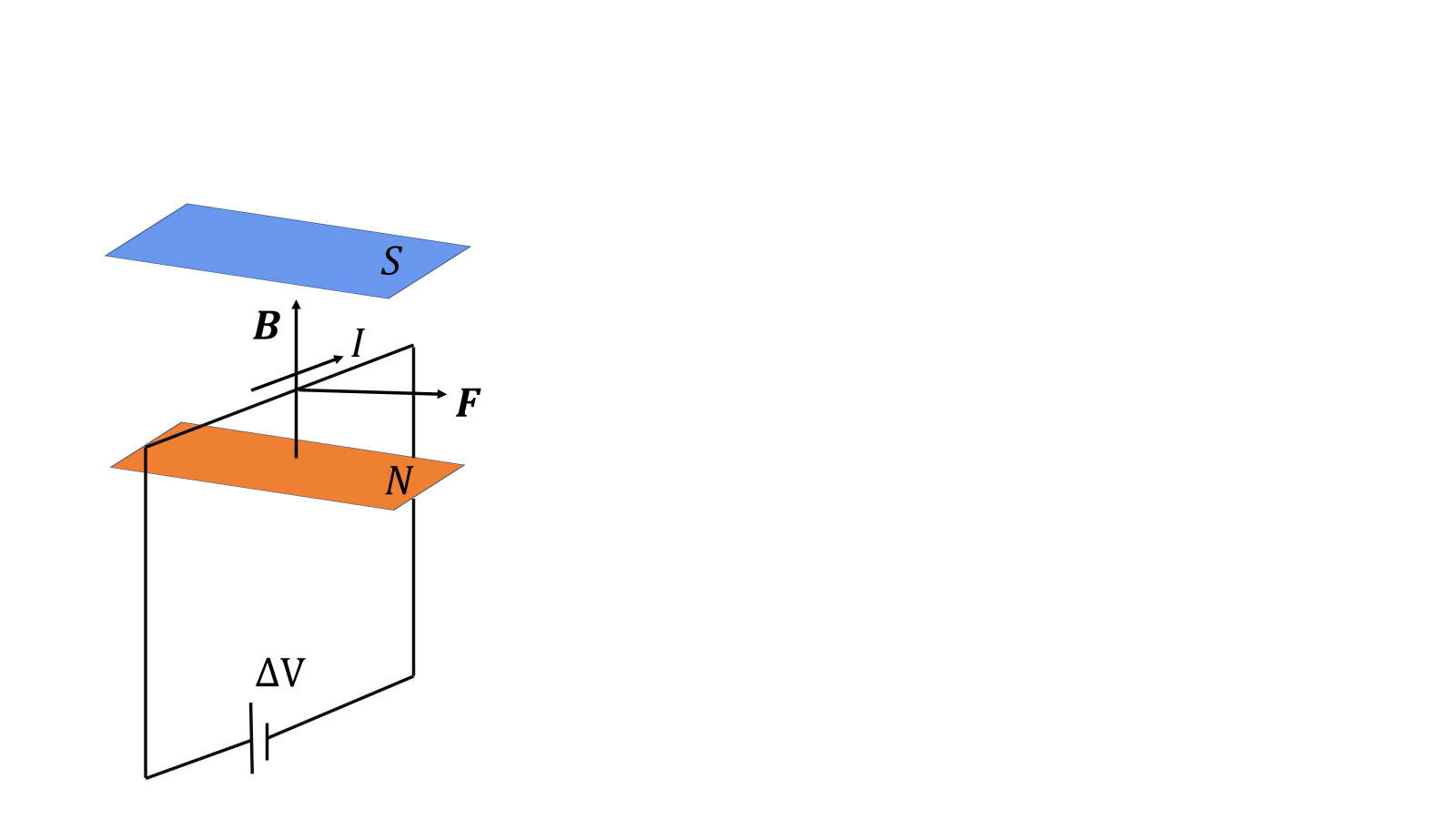
ローレンツ力は、上記のような簡単な実験で存在を確かめることができる。U字磁石か、棒磁石を2本、ケーブル、電源装置(電池)を用意する。図のように装置を組むと右ねじ方向に力が働くはずである。電流が電荷の速度に対応しているので、直列に電池を２本つなぐとローレンツ力も２倍になるはずである。磁場を２倍にするのは難しいと思うがもし２倍の磁場を作る磁石と取り換えればローレンツ力が２倍になるはずである。