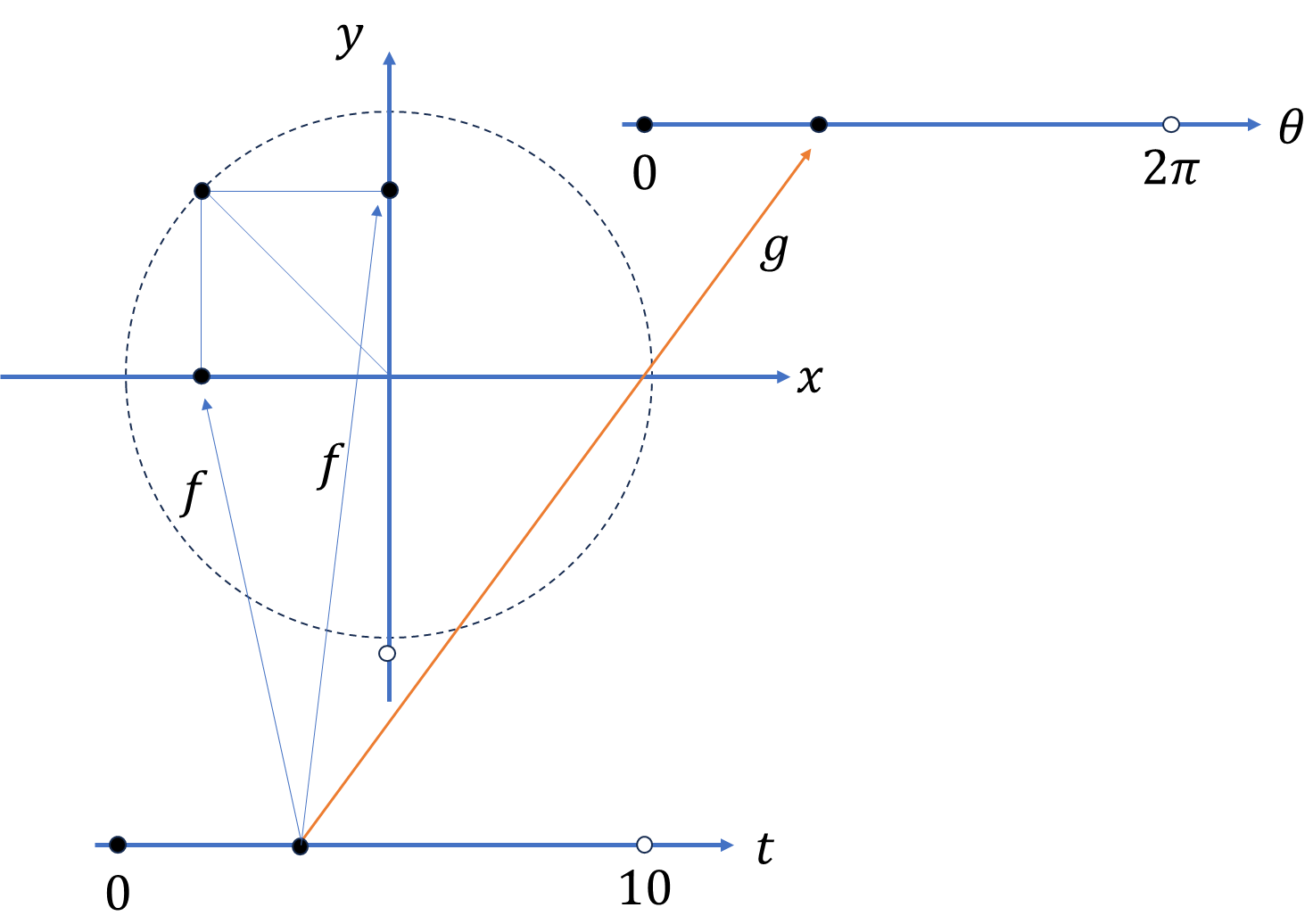多様体の定義がよく分からないし、そもそも使い方が分からないため必要な状況を無理やり作って理解を深める会です。

　この動画は原点\(O\)を中心に半径\(1\)の円を円周を\(10\)秒かけて1周して戻ってくる運動である。よく等速円運動と呼ばれたりする。角速度\(\omega\)を \[\omega:=\frac{2\pi}{周期}=\frac{2\pi}{10}\] と定義することで、物体の位置を直交座標で、 \[f(t)=(x,y)=(\cos\omega t,\ \sin\omega t)\] 極座標では、 \[g(t)=(r,\theta)=(1,\ \omega t)\] と表せる。

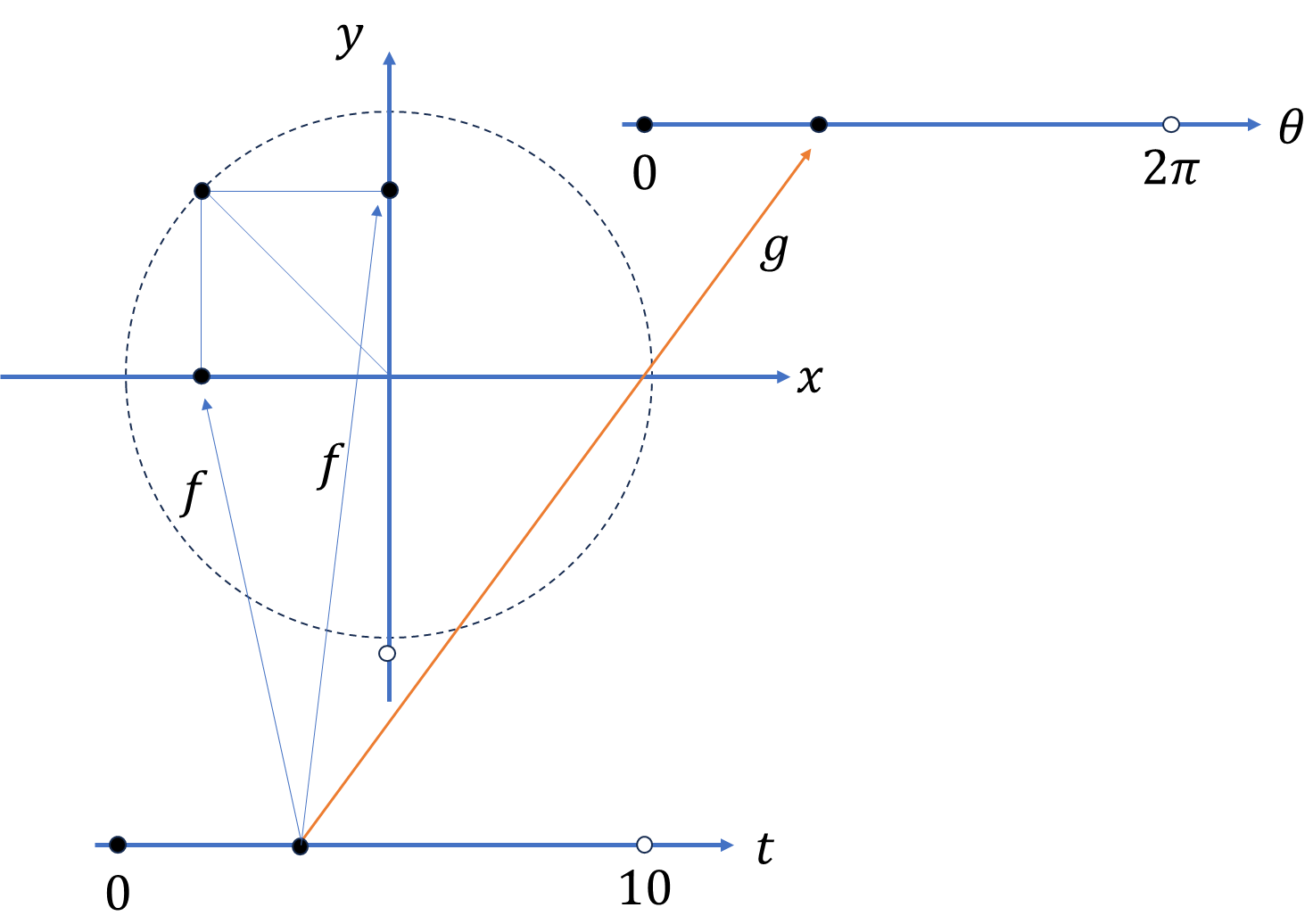
時間\(t\)を１つ決めれば、物体の位置\((x,y)\)が１つに決まる。また\(0\lt t\le10\)とすれば、物体の軌跡のいずれの点を取っても時間\(t\)と対応する。更に\(x,y\)と\(t\)は連続で、写像\(f\)により、\(t\)の滑らかな変化に対して\(x,y\)も(飛び飛びにならず)滑らかな変化をする。\(\theta\)も\(0\lt\theta\le2\pi\)とすれば、こちらも滑らかに変化する１対１対応で\(g:t\to(1,\theta)\)も連続写像である。 \[f\circ g^{-1}:(1,\theta)\to(x,y)\] このような合成写像を取ることで、\((x,y)\)と\((1,\theta)\)が滑らかに変化する１対１対応ということも分かる。この物体の速度は、 \[(v_x,v_y)=\left(\frac{dx}{dt},\frac{dy}{dt}\right)\] \[=\omega(-\sin\omega t,\ \cos\omega t)\] ではこの物体が時間\(t\le10\)の間に進んだ道のり\(l\)を求めてみよう。 \[dl=\sqrt{(dx)^2+(dy)^2}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\] \[=\omega dt\] であるため、 \[l=\int_0^ldl=\int_0^{t}\omega dt=\omega t=\theta\] とわかる。\(dl=\omega dt\)の置換は写像\(f\)が全単射な連続写像という確認の上できる。

一旦、\((1,\theta)\)と物体の軌跡が滑らかに変化する１対１対応であることは忘れて\((x,y)\)と\((1,\theta)\)との関係を求めよう。 \[(1,\theta)=\varphi(x,y)=\left(\sqrt{x^2+y^2},\ \arctan\frac{y}{x}\right)\] でよいだろうか。実はこれではよくない。

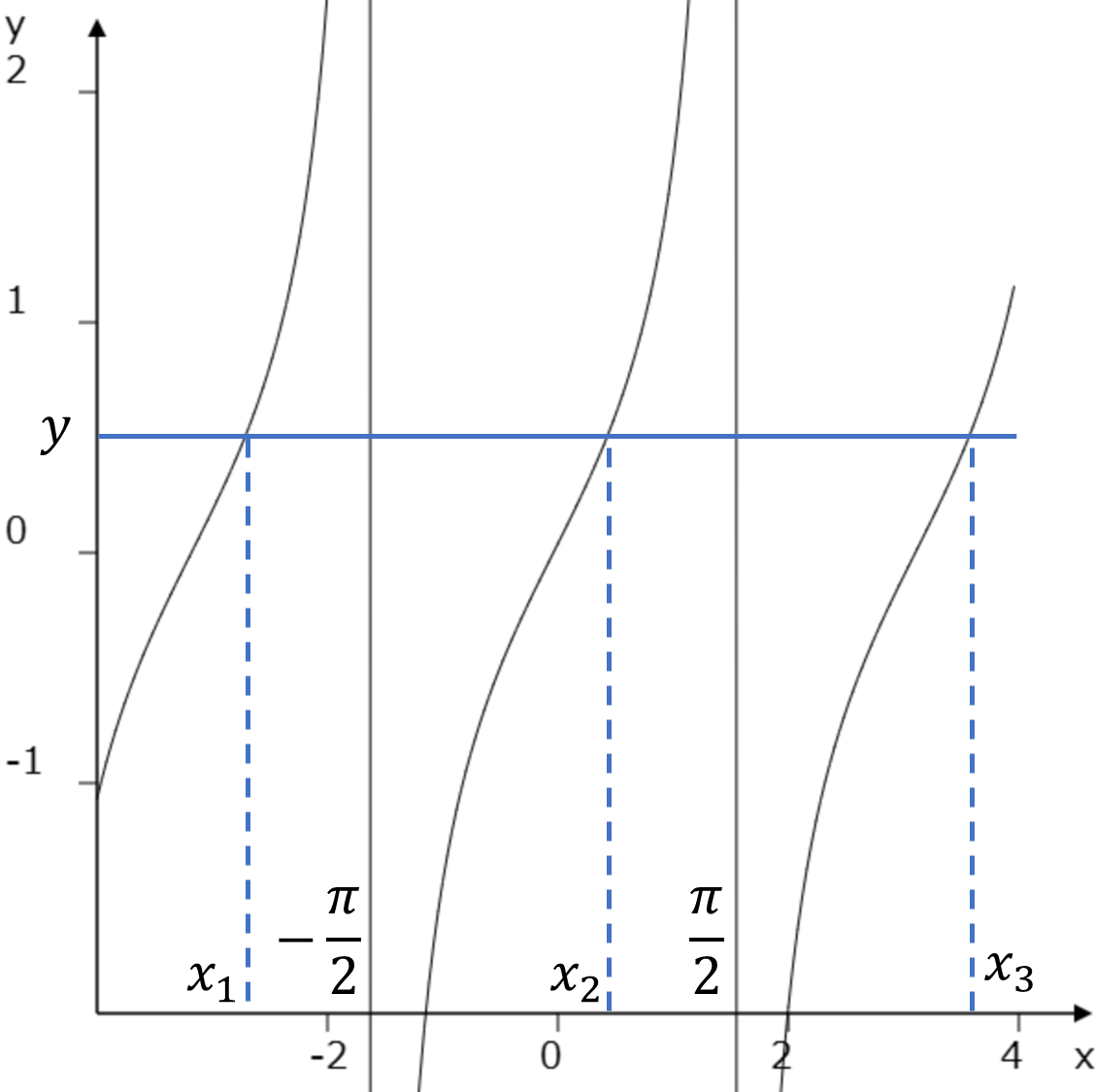
　これは\(y=\tan x\)のグラフで、\(x\)に対応した\(y\)が１つ決まる。しかし\(y\)を１つ決めると、対応する\(x\)は１つに定まらない。そこで定義域を固定してあげる必要がある。このページでは、\(\tan x\)の定義域を \[-\frac{\pi}{2}\lt x\lt \frac{\pi}{2}\]と定める。これにより、\(y\in\mathbb{R}\)に対して、\(x\in(-\pi/2,\ \pi/2)\)が常に１つ定まる関係性が作れる。これが\(\tan x\)逆関数\(\arctan x\)である。

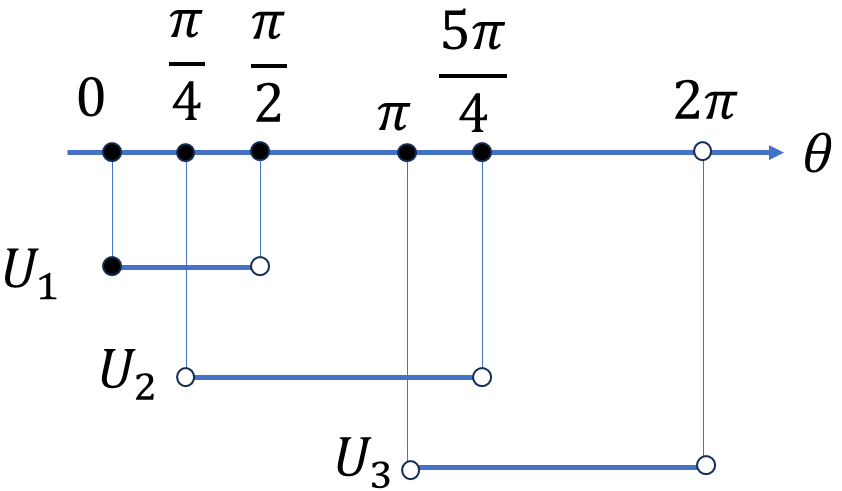
　\(1,\theta\)と\(x,y\)の関係を正確に記述するために集合\(U_1,U_2,U_3\)を、 \[U_1=\{(1,\theta)\ |\ 0\le\theta\lt\frac{\pi}{2}\}\] \[U_2=\{(1,\theta)\ |\ \frac{\pi}{4}\lt\theta\lt\frac{5\pi}{4}\}\] \[U_3=\{(1,\theta)\ |\ \pi\lt\theta\lt2\pi\}\] としよう。今回考える\((1,\theta)\)全体を\(M\)とすれば、 \[M=\bigcup_{i=1}^3 U_i=U_1\cup U_2\cup U_3\] と表せる。\(M\)は\(U_1,U_2,U_3\)で覆うことができる。

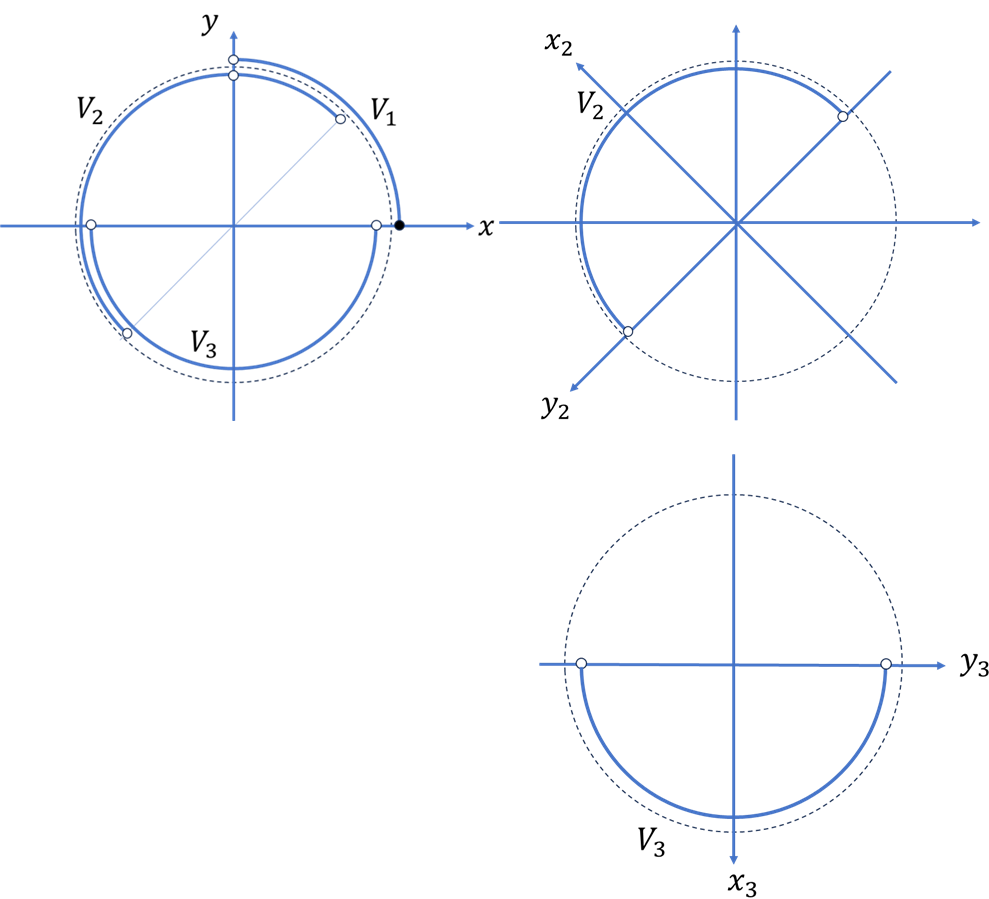
　我々が見ている物体が運動をしているユークリッド平面\(\mathbb{R}^2\)にも3つの座標系を取る。\(x,y\)は直交座標で、\(x_2,y_2\)は原点を中心に\(3\pi/4\)傾いている座標系、\(x_3,y_3\)は\(3\pi/2\)傾いている。これで準備ができた。 \[U_1=\varphi_1^{-1}(x,y)=\left(\sqrt{x^2+y^2},\arctan \frac{y}{x}\right)\] \[U_2=\varphi_2^{-1}(x_2,y_2)=\left(\sqrt{x^2+y^2},\arctan \frac{y_2}{x_2}+\frac{3\pi}{4}\right)\] \[U_3=\varphi_3^{-1}(x_3,y_3)=\left(\sqrt{x^2+y^2},\arctan \frac{y_3}{x_3}+\frac{3\pi}{2}\right)\] となる写像\(\varphi_1,\varphi_2,\varphi_3\)を用意しよう。図の曲線\(V_1,V_2,V_3\)は、 \[\varphi_1:U_1\to V_1\] \[\varphi_2:U_2\to V_2\] \[\varphi_3:U_3\to V_3\] であり、\(U_i\)と\(V_i\)は１対１の対応になっていることが分かる。

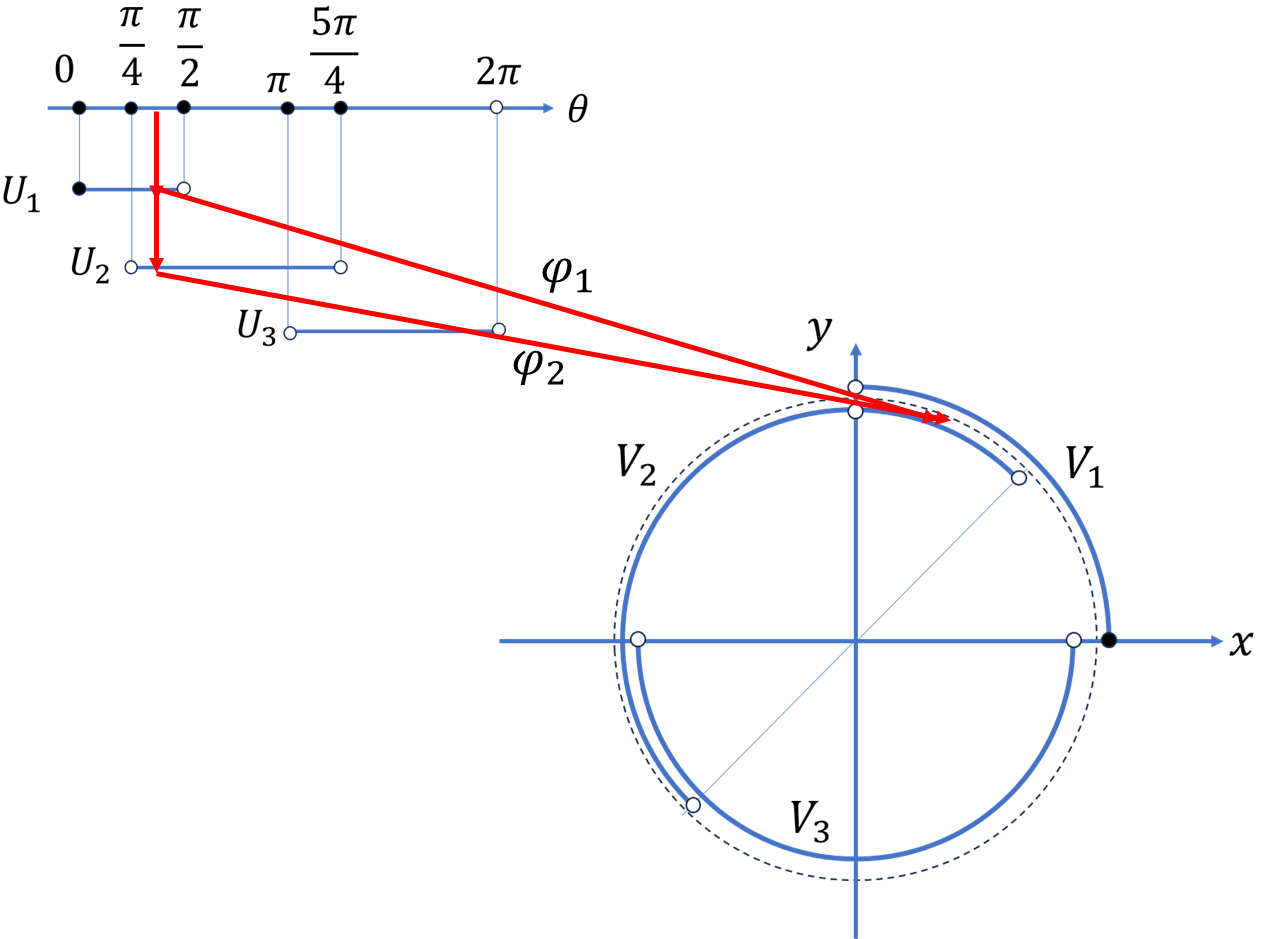
　任意の\((1,\theta)\in M\)について、いずれかの\(\{U,\varphi_i\}\)の組を使うことで、経路上の１点が定まっている。この対応関係を上手く使って物体の進んだ経路\(l\)を求めてみよう。\(\theta\in(-\pi/2,\pi/2)\)について、 \[y=x\tan\theta\] を\(x^2+y^2=1\)に代入する。 \[x^2+x^2\tan^2\theta=1,\ x=\frac{\pm1}{\sqrt{1+\tan^2\theta}}\] であるから、 \[\frac{dx}{d\theta}=\frac{\pm\tan\theta}{\sqrt{1+\tan^2\theta}^3}\frac{1}{\cos^2\theta}\] \[=\frac{\pm\tan\theta}{\sqrt{1+\tan^2\theta}^3}(1+\tan^2\theta)=\frac{\pm\tan\theta}{\sqrt{1+\tan^2\theta}}\] 以上より \[dx=\pm\frac{\tan\theta d\theta}{\sqrt{1+\tan^2\theta}}\tag{1}\] \(x^2+y^2=1\)の両辺を\(x\)で微分すると \[2x+2y\frac{dy}{dx}=0,\ \frac{dy}{dx}=-\frac{x}{y}=-\frac{1}{\tan\theta}\tag{2}\] ただし\(y,\ \tan\theta\neq0\)である。 \[dl=\sqrt{(dx)^2+(dy)^2}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}|dx|\] (2)、(1)を代入すると、 \[dl=\sqrt{1+\frac{1}{\tan^2\theta}}\frac{\tan\theta d\theta}{1+\tan^2\theta}=d\theta\tag{3}\] この式は\(y,\tan\theta\)を含まない式で、\(y,\ \tan\theta=0\)でも大丈夫。しかし、\(\theta\lt \pi/2\)で一回転する物体の運動を記述できない。これを解決してくれるのが\(V_2=\varphi_2(U_2),\ V_3=\varphi_2(U_3)\)である。

　(i)　物体が、\(V_1-(V_1\cap V_2)\)上にいる時 \[l=\int_0^{l}dl=\int_0^\theta d\theta=\theta\]

　(ii)　物体が、\(V_2-(V_2\cap V_3)\)上にいる時

　(iii)　物体が、\(V_3\)上にいる時

　\(y_3=x_3\tan(\theta-3\pi/2)\)であるから、同様の計算をして、 \[l=\int_{V_1-(V_1\cap V_2)+V_2-(V_2\cap V_3)}dl+\int_{\pi}^l dl\] \[=\pi+\int_\pi^\theta d\theta=\theta\] 時間\(t\)を使った時と同様の結果を得られた。

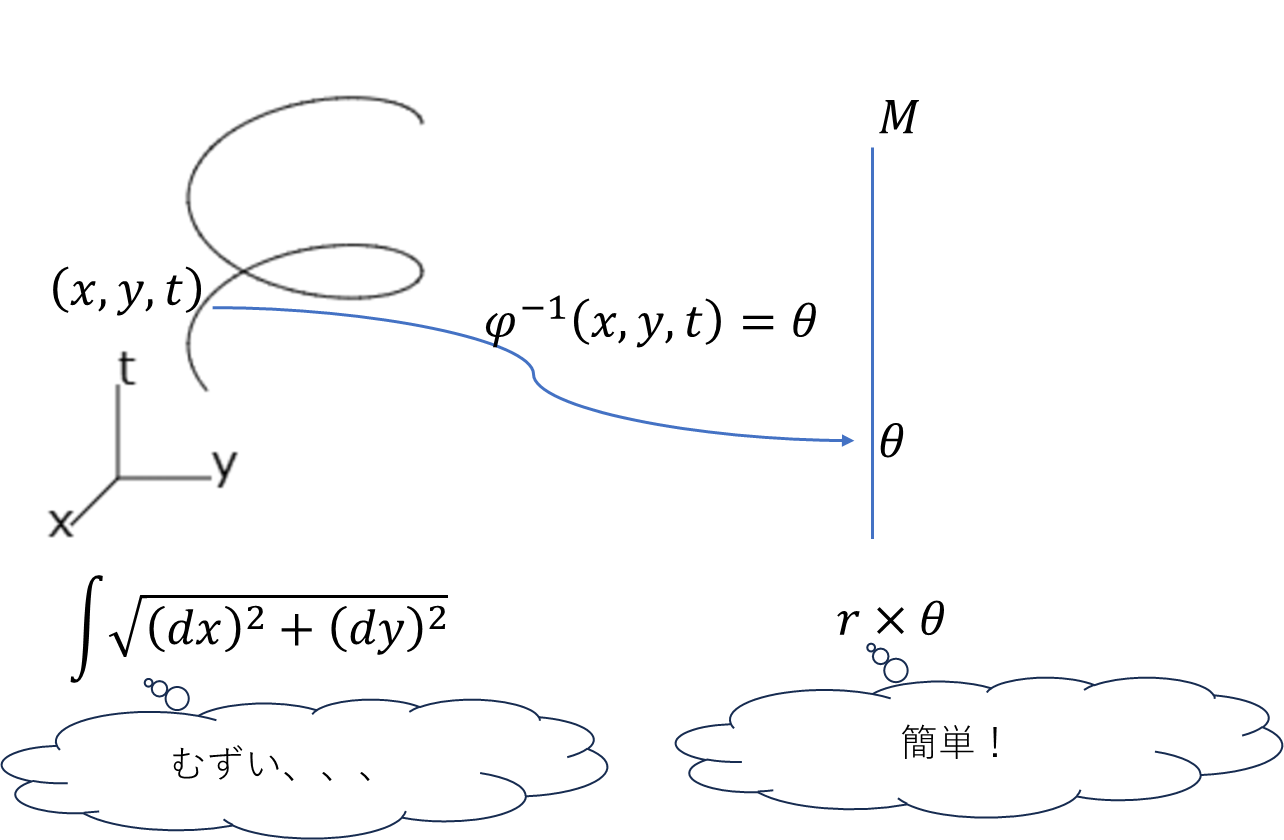
　ある座標系で解くことが難しい問題でも別の座標系で簡単に解けることがある。多様体がやりたいことの１つとしてこの座標変換があると思う。上手い1対1の連続な対応が見つからなくても、各部分でうまい対応が見つかれば座標変換できるというのは、便利である。