/*　この章では変分原理というものを解説しよう。変分原理によって新たな物理法則の発見や、今まで説明できなかった現象が説明できる！とかはありません。しかし、理論体系がとてもきれいなので、

終わり　*/

　いきなり最小作用の原理やラグランジュ関数に触れても何のために立っているか、意味が分からないと思うので、ここでは変分法を理解するためにフェルマーの原理について書いていく。

　図のように光が、点\(a\)から点\(b\)まで直進しているとしよう。光は直進するのだが、いまは光が直進するということは忘れて

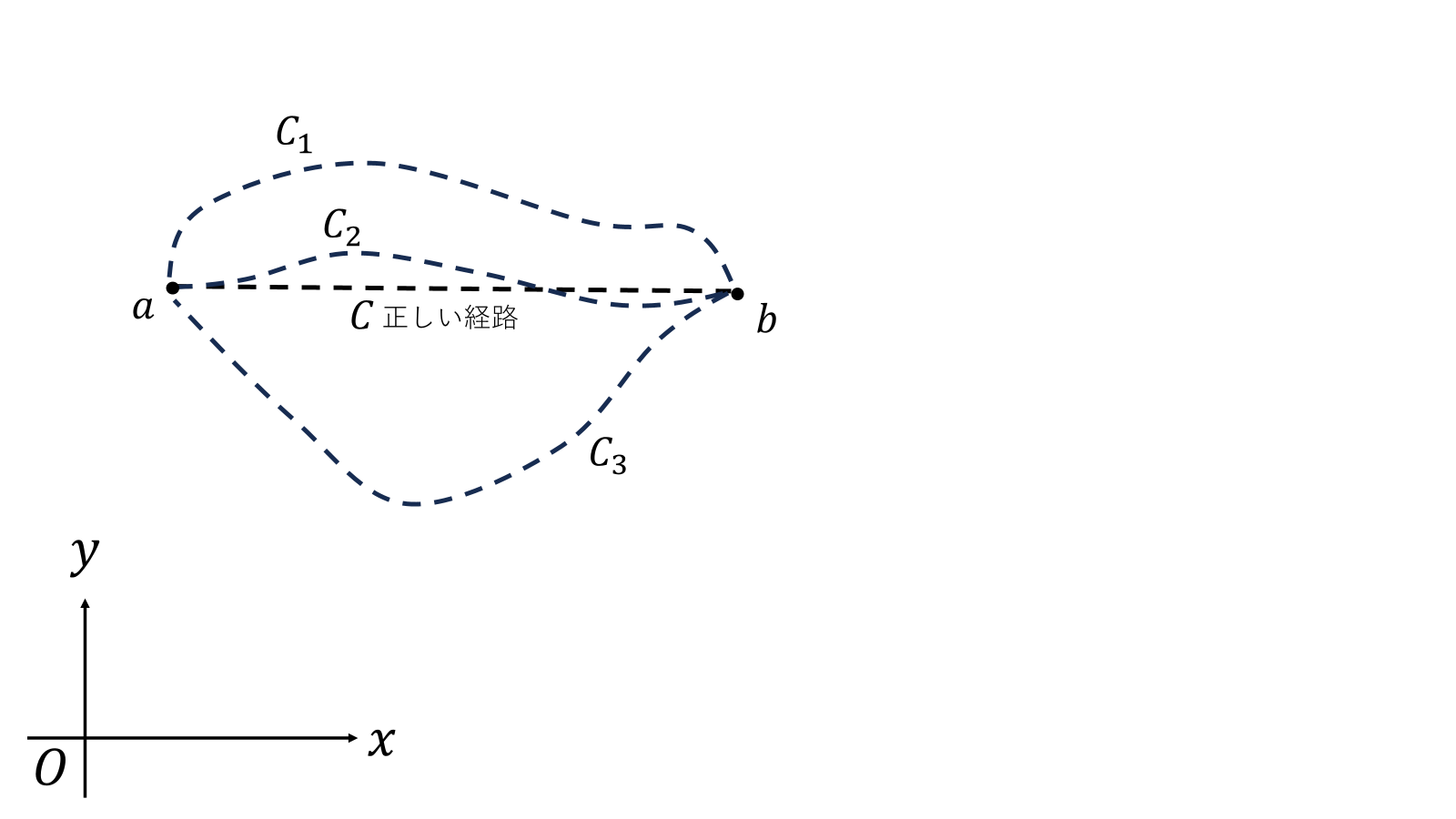
　いろいろな経路を想定しよう。このいろいろな経路がある中で、光が光速度\(c=1/\sqrt{\epsilon\mu}\)で時間最小でたどり着ける経路について考えよう。

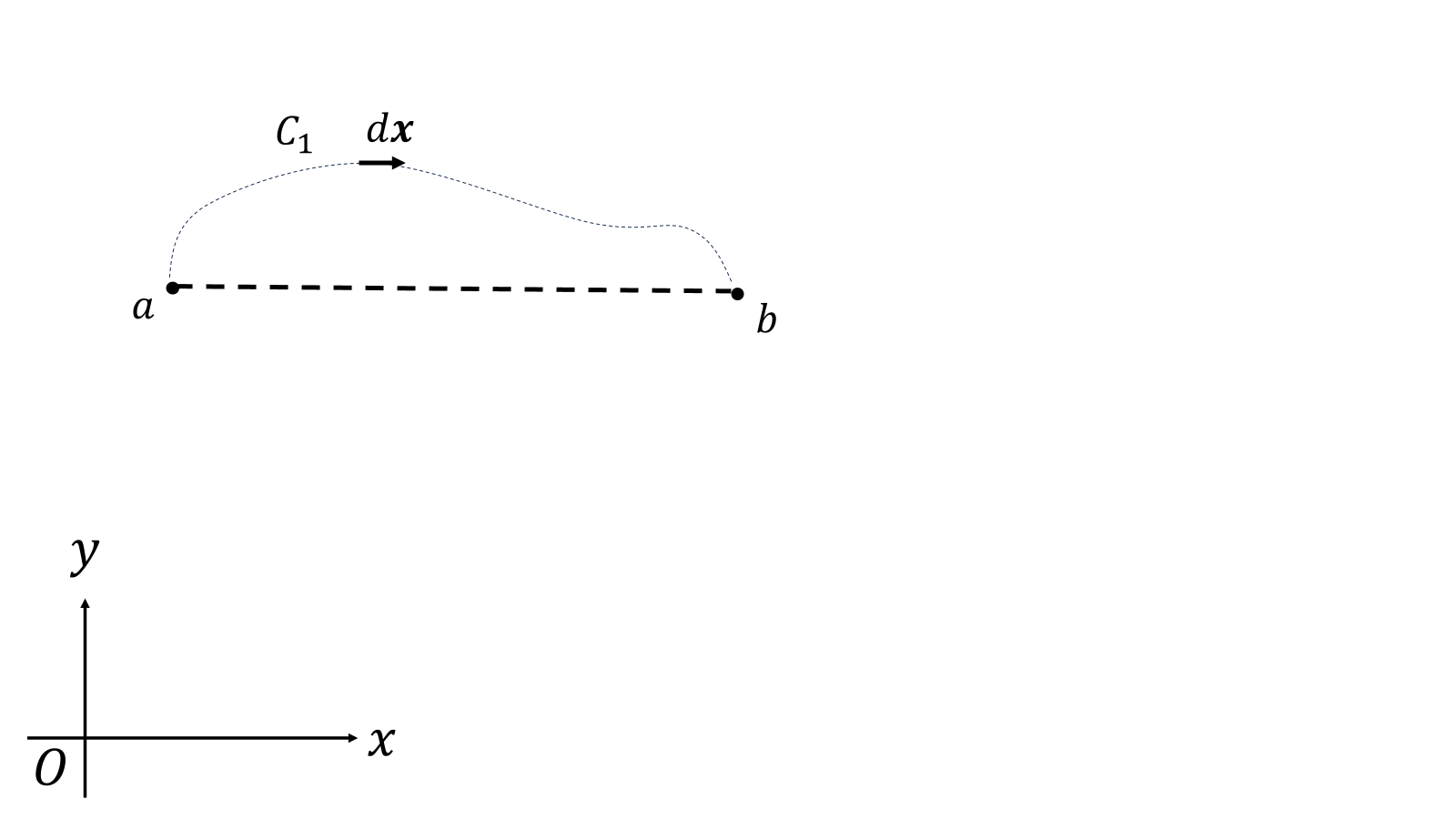
　とても短い道のり\(d\boldsymbol{x}\)進むのにかかる時間\(dt\)は、 \[dt=\frac{|d\boldsymbol{x}|}{c}=\frac{\sqrt{dx^2+dy^2}}{c}\] と表せる。経路\(C_1\)で、\(a\)から\(b\)にたどり着くのにかかる時間を\(T_{C1}\)とすると、 \[T_{C1}=\int_{C1}\frac{\sqrt{dx^2+dy^2}}{c}\] のように表せる。ここで、\(dy/dx=\delta(x)\ (\delta(a),\delta(b)=0)\)となる適当な関数\(\delta(x)\)を使うことで、任意の経路\(C_n\)での時間\(T\)は \[T_{Cn}=\int_a^b\frac{\sqrt{1+(dy/dx)^2}}{c}dx\] \[T_{Cn}=\int_a^b\frac{\sqrt{1+\delta(x)^2}}{c}dx\] である。\(a\)から\(b\)にだどりつくまでの時間\(T\)を\(\delta\)の関数とみて、 \[T(\delta)=\int_a^b\frac{\sqrt{1+\delta^2}}{c}dx\] が最小値(極小値)を取るとき、光は直進するともいえる。このように、なんだかの変数\(\delta\)とその関数\(T(\delta)\)を用意して、\(T\)の極値問題を使って解く方法を変分法と言ったりする。もっとも簡単な例は、 \[x^2+4x-6=0\] の最小値\((-2,-10)\)を求める問題で、平方完成を使わずに、\(y=x^2+4x-6\) と置き、\(y'=2x+4=0\)のように極値の問題として解くということである。筆者が高校生の頃は分数の計算が苦手で、平方完成をせずに、極値問題として解いていた。

＊＊光の直進＊＊

　光の直進は、光が時間最小の経路を選ぶ、と言い換えることができる。

　次に光は媒質が違うと屈折するという性質がある。

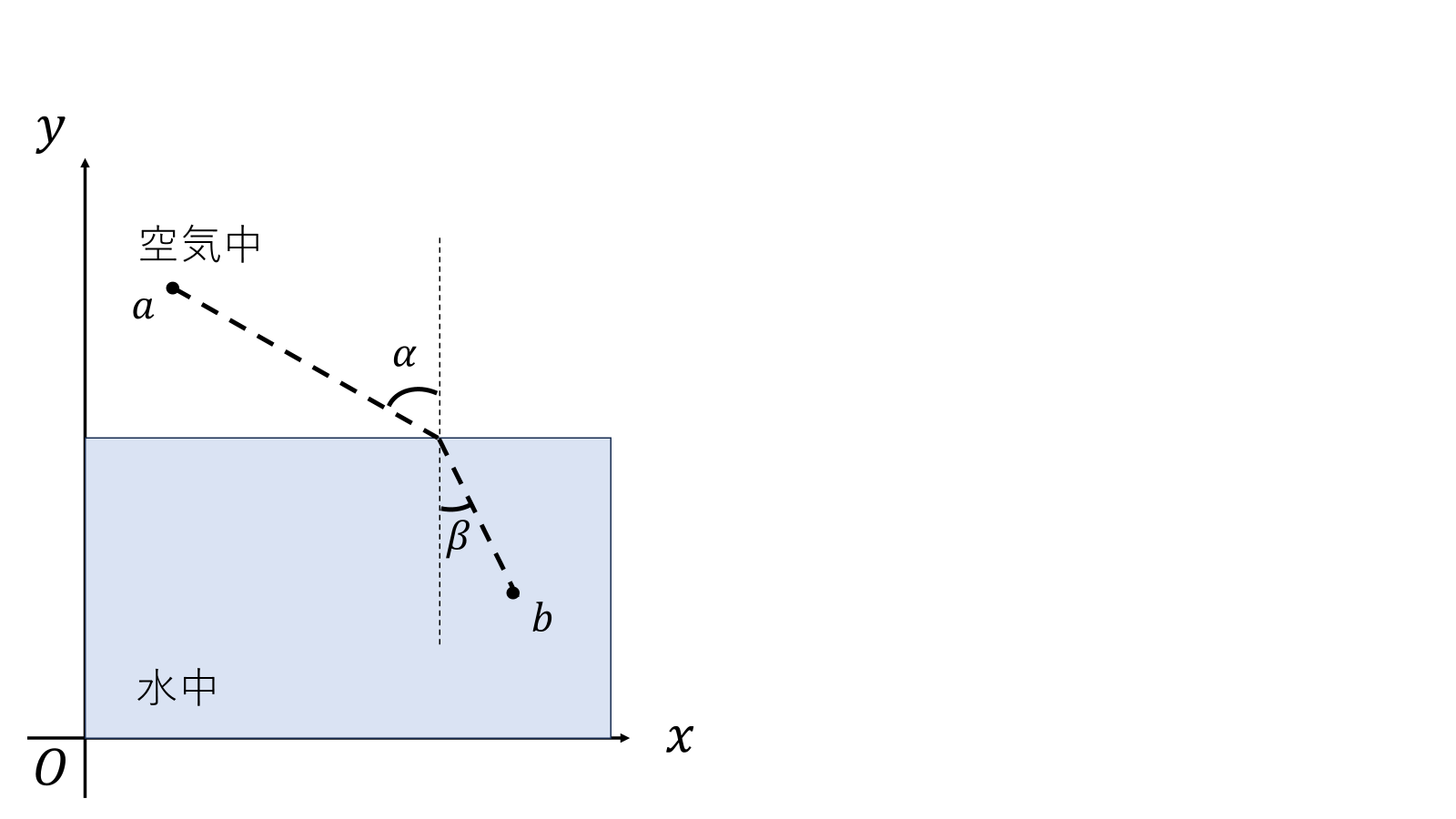
　光の屈折はスネルの法則により \[\frac{\sin\alpha}{\sin\beta}=\frac{c_A}{c_B}\] のように表せる。\(\alpha\)は入射角、\(\beta\)は反射角、\(c_A\)は空気中の光の速さ、\(c_B\)は水中の光の速さである。

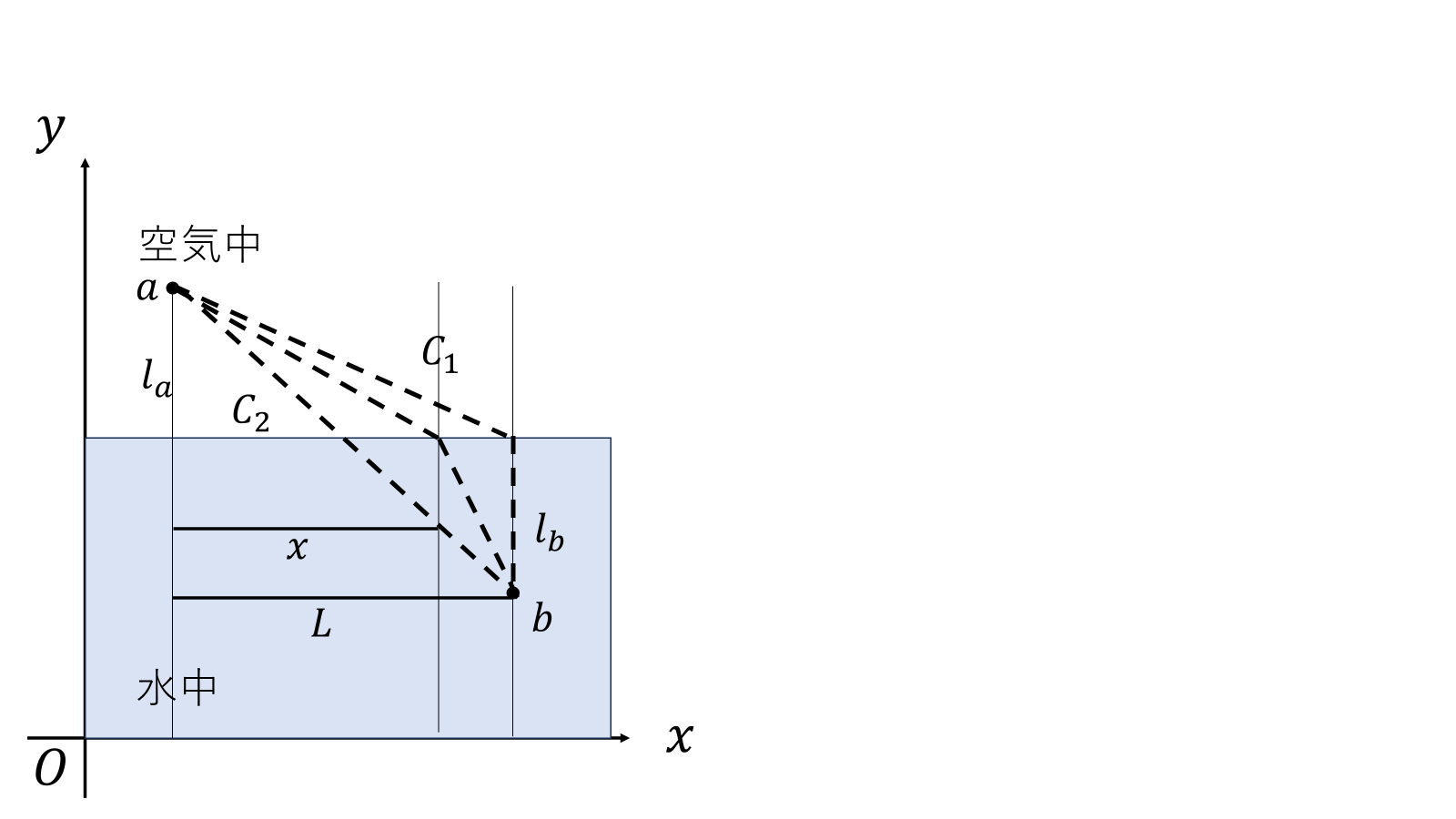
　この法則も変分法を使って求めることができる。\(a\)から\(b\)にいたるまでの時間を\(T\)とするとき、距離が最短の\(C_2\)を選ぶべきか、空気中の光の速さのほうが早いので\(C_1\)を選ぶが。とりあえず先ほどのように光の直進のように時間最小\(T\)を探そう。同じ媒質中は直進することは分かっているので、図のように変数を設定すると、点\(a\)から水面までの距離は、 \[\sqrt{x^2+(l_a)^2}\] である。水面にたどり着くまでにかかる時間は、 \[\frac{1}{c_A}\sqrt{x^2+(l_a)^2}\] である。 同様の計算で、水面から、点\(b\)にたどり着くまでの時間は、 \[\frac{1}{c_B}\sqrt{(L-x)^2+(l_b)^2}\] のように計算できる。\(a\)から\(b\)にたどり着く時間\(T\)は、 \[T(x)=\frac{1}{c_A}\sqrt{x^2+(l_a)^2}+\frac{1}{c_B}\sqrt{(L-x)^2+(l_b)^2}\] 今回は\(x\)の関数としてみた。\(x\)が小さすぎれば、\(C_2\)のようにゆっくりしか進めない、水中が長くなり、\(T\)が大きくなる。\(x\)が大きすぎれば\(C_1\)のように経路が長くなり、\(T\)が大きくなる。この間に\(dT/dx=0\)となる極値つまり\(T\)の最小値があるはずだ。 \[\frac{d}{dx}T(x)=\frac{1}{c_A}\frac{2x}{2\sqrt{x^2+(l_a)^2}}+\frac{1}{c_B}\frac{-2(L-x)}{2\sqrt{(L-x)^2+(l_b)^2}}=0\] \[\frac{x}{\sqrt{x^2+(l_a)^2}}=\sin\alpha,\ \frac{(L-x)}{\sqrt{(L-x)^2+(l_b)^2}}=\sin\beta\] なので、 \[\frac{d}{dx}T(x)=\frac{1}{c_A}\sin\alpha-\frac{1}{c_B}\sin\beta=0\] \[\frac{\sin\alpha}{\sin\beta}=\frac{c_A}{c_B}\] と時間最小の経路から、スネルの法則を導くことができた。

＊＊光の屈折＊＊

　光の屈折はスネルの法則により、 \[\frac{\sin\alpha}{\sin\beta}=\frac{c_A}{c_B}\] と表せる。これも光が時間最小の経路を選ぶことから説明が付く。

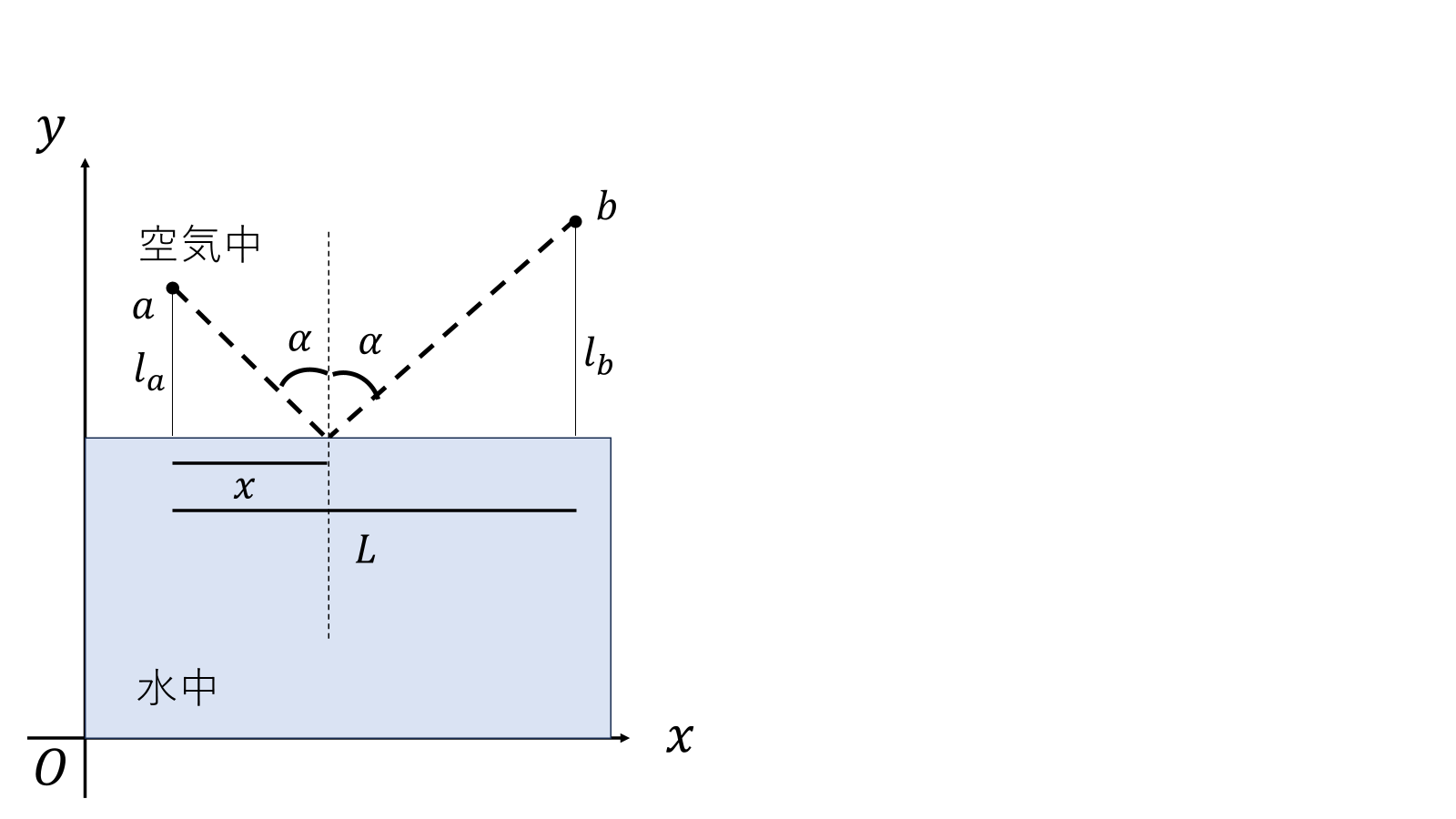
　光には反射の法則、水面で反射する光は入射角、反射角が等しい。これも時間最小から考えると、 \[T(x)=\frac{1}{c_A}\sqrt{(l_a)^2+x^2}+\frac{1}{c_A}\sqrt{(l_b)^2+(L-x)^2}\] である。\(T\)の極小値を考えるため\(x\)微分すると、 \[\frac{d}{dx}T(x)=\frac{x}{c_A\sqrt{(l_a)^2+x^2}}-\frac{L-x}{c_A\sqrt{(l_b)^2+(L-x)^2}}=0\] 入射角を\(\alpha\)、反射角を\(\beta\)とすると、 \[\frac{x}{\sqrt{(l_a)^2+x^2}}=\sin\alpha,\ \frac{L-x}{\sqrt{(l_b)^2+(L-x)^2}}=\sin\beta\] であるから、 \[\frac{d}{dx}T(x)=\frac{1}{c_A}\sin\alpha-\frac{1}{c_A}\sin\beta=0\] \[\sin\alpha=\sin\beta\] つまり、時間最小の経路を考えると、入射角と反射角が等しくなる。

＊＊フェルマーの原理＊＊

　光のは時間最短の経路を選ぶ。

　光は直進する、屈折の法則、反射の法則がなんと、フェルマーの原理の時間最短の経路で説明がつく。いままで別の法則に見えていたものが、同じ法則で説明できるっていうのがより原理的で、より真理に近い記述をしているようで、かっこいいですね。