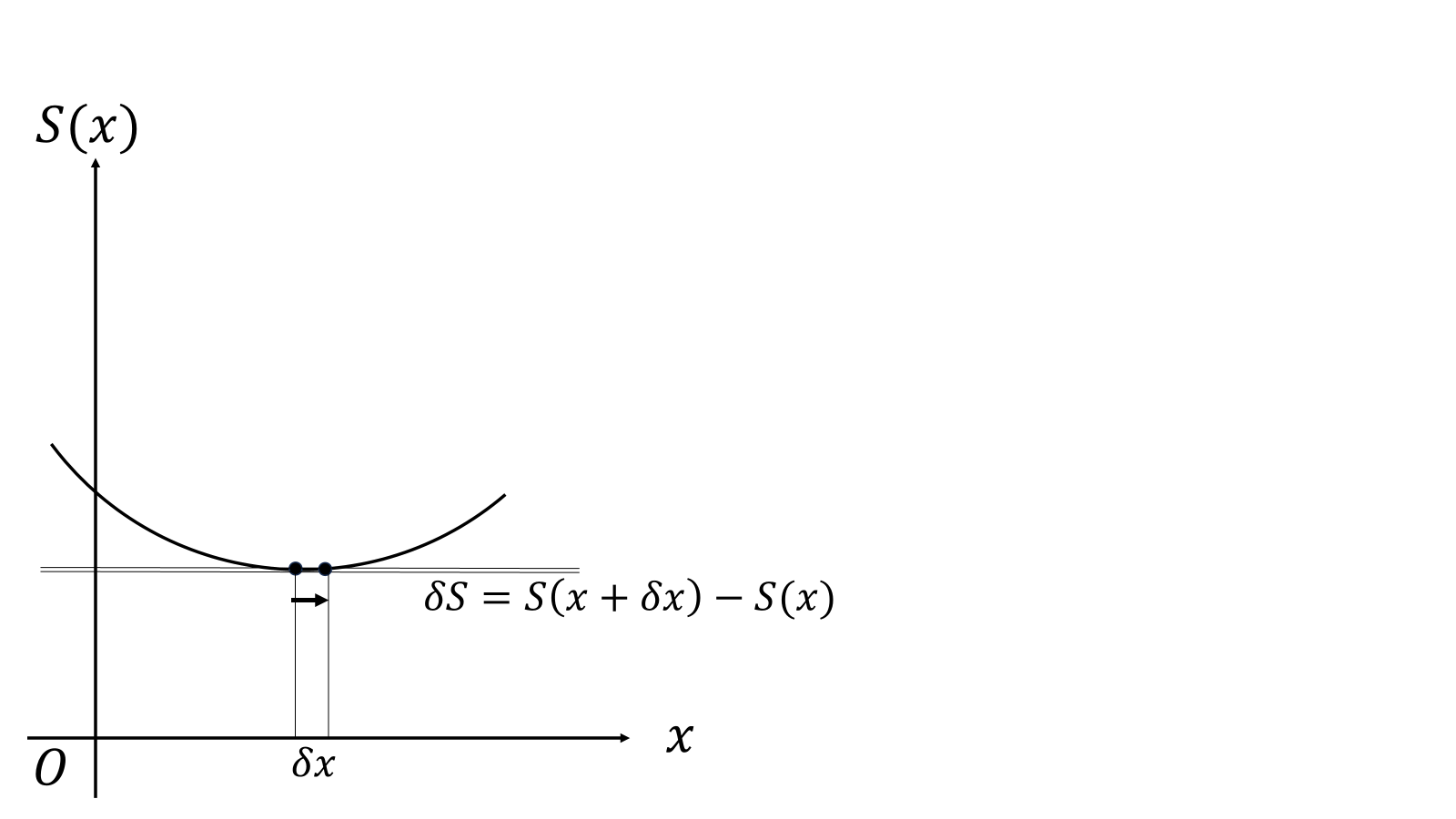/*　重要

　今回紹介するラグランジアンについてだか、なぜこのような形なのだろか、とあまり考えないほうがいいかもしれない。筆者も長いこと考えてきたが、結局この定義で、運動方程式が導かれるからという結果論である。運動方程式を変分法の問題にしたものが、ラグランジアンの時間積分だ。

終わり　*/

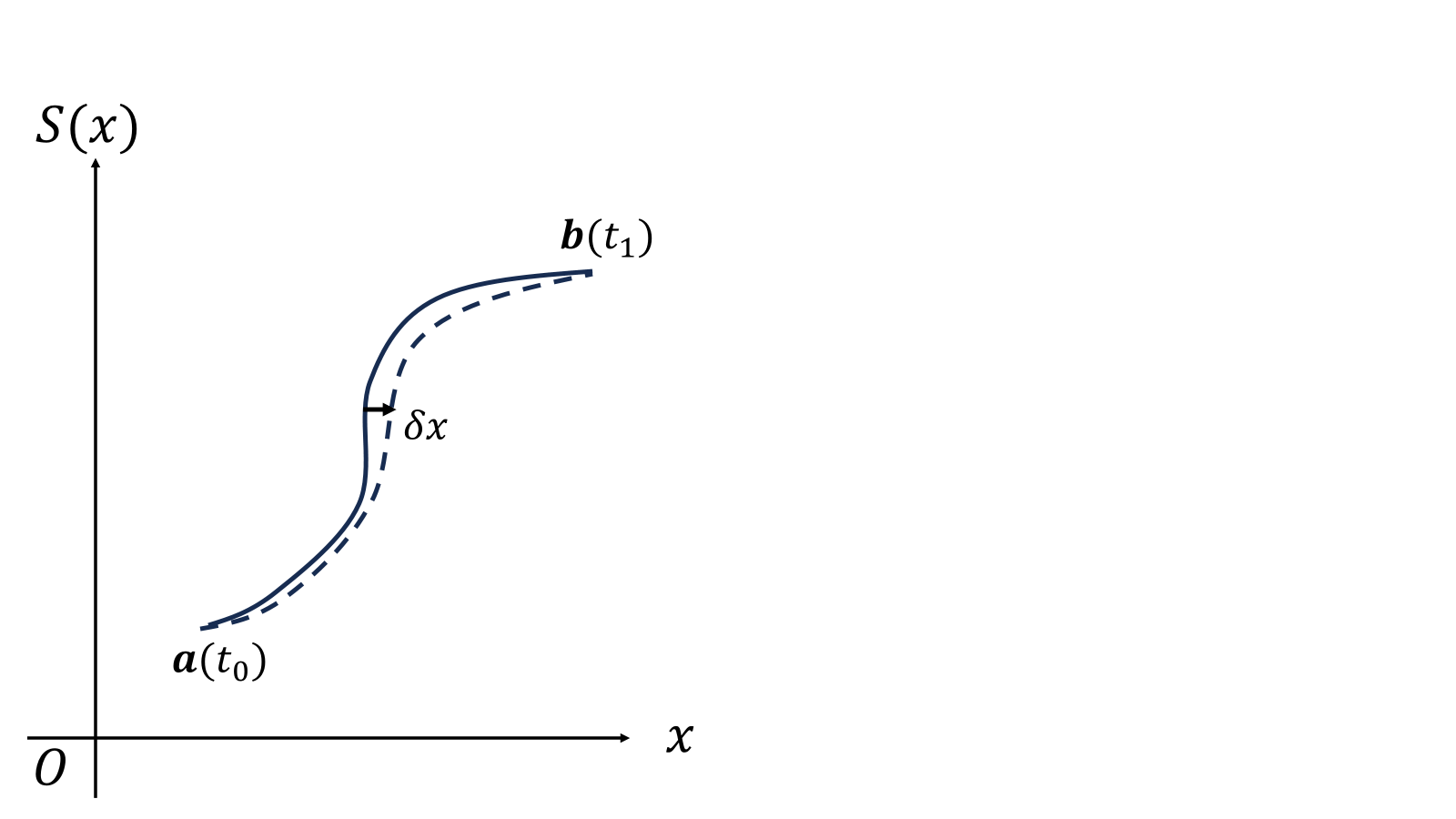
前回は光の経路を決める変分法の例としてフェルマーの原理をやった。今回は変分法を用いて運動する物体の経路を決めたい。光のように運動する速さが決まっていないので、時間\(t_0\)で点\(\boldsymbol{a}\)、時間\(t_1\)で点\(\boldsymbol{b}\)に物体があるという条件を付けよう。フェルマーの原理では、時間\(T\)が極値になることを考えたが、今回は \[S:=\int^{t_1}_{t_0}L(x,y,\dot x,\dot y,t)dt\] と定義される作用\(S\)の極値を求めよう。ラグランジアン\(L\)は、どのように定義するかは後で決める。\(x\)を少しずらして、\(x+\delta x\)としよう。 \[x\mapsto x+\delta x\] ならば \[\dot x\mapsto\frac{d}{dt}(x+\delta x)=\dot x+\delta\dot x\] になるのでラグランジアンは、 \[L(x+\delta x,y,\dot x+\delta\dot x,\dot y,t)\] \[\simeq L(x,y,\dot x,\dot y,t)+\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\delta\dot x\] ここでは\(\delta x,\delta\dot x\)について一次式の近似をした。微小量の変化では厳密に\(f(x+dx)=f(x)+\frac{df}{dx}dx\)である。

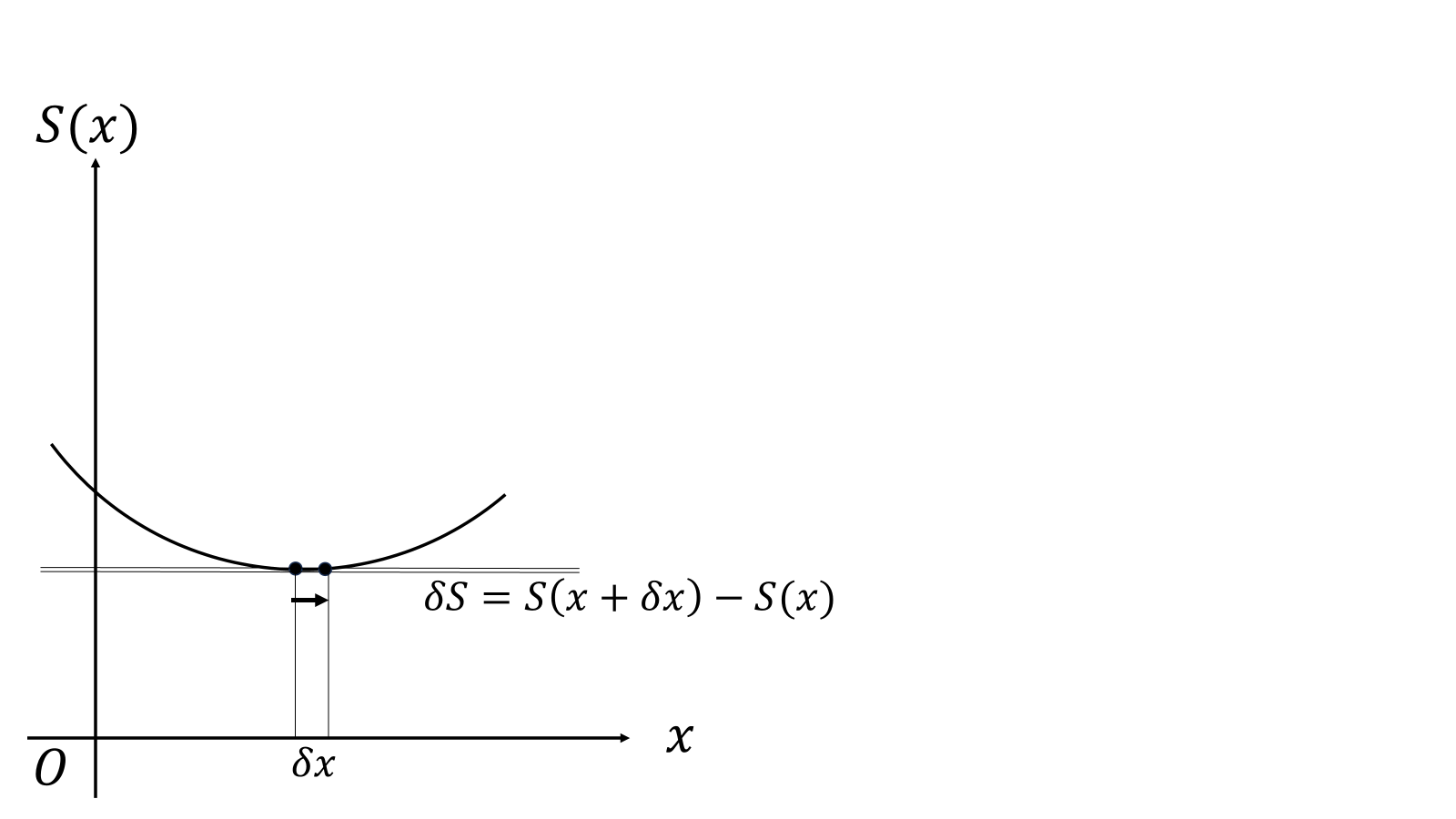
　作用が極値を取るならば、\(x\)を少しずらして、\(x+\delta x\)としても作用\(S\)はほとんど変化しないので、 \[\delta S=S(x+\delta x)-S(x)\simeq0\] とみなせる。 \[\delta S=\int_{t_0}^{t_1}L(x+\delta x,y,\dot x+\delta\dot x,\dot y,t)dt\] \[-\int_{t_0}^{t_1}L(x,y,\dot x,\dot y,t)dt\] \[=\int_{t_0}^{t_1}\left(L(x,y,\dot x,\dot y,t)+\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\delta\dot x\right)dt\] \[-\int_{t_0}^{t_1}L(x,y,\dot x,\dot y,t)dt\] \[=\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial\dot x}\delta\dot x\right)dt\] 積の微分\(y(dx/dt)=d(xy)/dt-x(dy/dx)\)を２項目に使ってあげると、 \[=\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x}\delta x+\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x}\delta x\right)-\frac{d}{dt}\frac{\partial L}{\partial\dot x}\delta x\right)dt\] \[=\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x}\delta x-\frac{d}{dt}\frac{\partial L}{\partial\dot x}\delta x\right)dt\frac{d}{dt}+\left(\frac{\partial L}{\partial\dot x}\delta x(t_0)-\frac{\partial L}{\partial\dot x}\delta x(t_1)\right)\] 時刻\(t_0\)に\(\boldsymbol{a}\)、時刻\(t_1\)に\(\boldsymbol{b}\)と決められているので、\(\delta x(t_0)=\delta x(t_1)=0\)である。 \[\delta S=\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x}\delta x-\frac{d}{dt}\frac{\partial L}{\partial\dot x}\delta x\right)dt=0\] \[\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x}-\frac{d}{dt}\frac{\partial L}{\partial\dot x}\right)\delta xdt=0\] 常に\(\delta x=0\)とは限らないので、 \[\frac{\partial L}{\partial x}-\frac{d}{dt}\frac{\partial L}{\partial\dot x}=0\] この式はオイラー・ラグランジュ方程式と呼ばれている。\(y\)方向に\(\delta y\)だけずらせば、 \[\frac{\partial L}{\partial y}-\frac{d}{dt}\frac{\partial L}{\partial\dot y}=0\] のような方程式を得ることもできる。この方程式を満たす条件は\(\delta S=0\)つまり作用\(S\)が極値を取るときである。

＊＊最小作用の原理＊＊

　ラグランジアン\(L(x_i,\dot x_i,t)\quad(x_i=x,y,z)\)について、 \[S:=\int_{t_0}^{t_1}L(x_i,\dot x_i,t)dt\] で定義される作用\(S\)は、位置\(x_i\)の関数とみて極値を取るとき、オイラー・ラグランジュ方程式 \[\frac{\partial L(x_i,\dot x_i,t)}{\partial x_i}-\frac{d}{dt}\frac{\partial L(x_i,\dot x_i,t)}{\partial\dot x_i}=0\] を満たす経路を選ぶ。

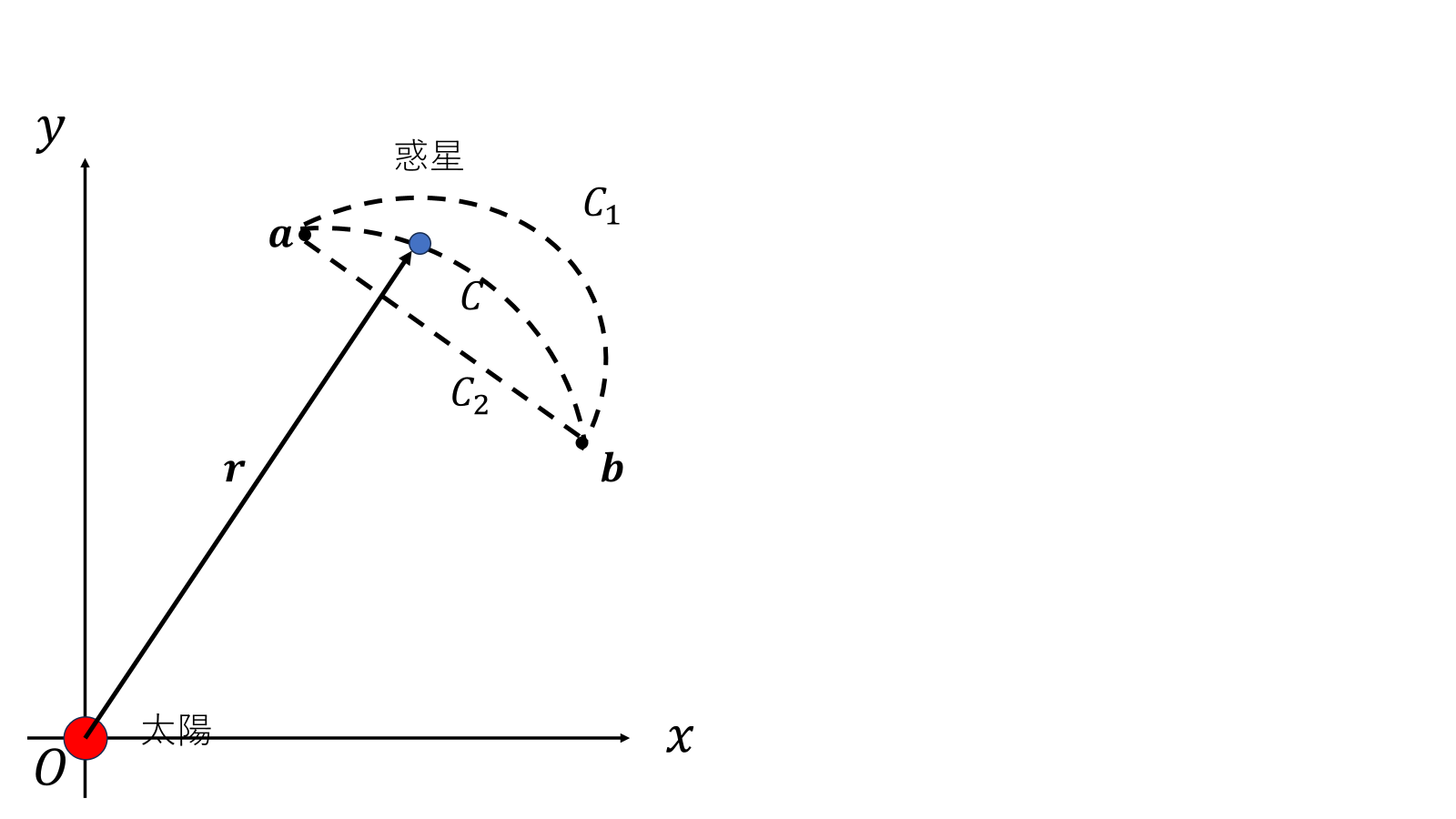
　ではラグランジアン\(L\)を決めて、オイラー・ラグランジュ方程式を意味のあるものにしよう。まずはラグランジアンはスカラーなので、エネルギーを使って記述しよう。\(\delta S=0\)のとき、\(C\)のような経路を実現するために、 \[L=\frac{1}{2}m(\dot x+\dot y)^2+\frac{GMm}{\sqrt{x^2+y^2}}\] のようなラグランジュ関数を取ってみよう。\(C1\)のように遠回りな経路を取ると太陽から遠いので\(r\)が大きくなり第２項目を小さくできるが、遠すぎると経路が長くなり、\(t_1\)に間に合うように\(v\)を大きくしないといけいない。\(C2\)のように最短経路を取って、第１項目を小さくしようとすれば、第２項目が大きくなる。このラグランジアンをオイラー・ラグランジュ方程式に代入すると、 \[\frac{\partial L}{\partial x}-\frac{d}{dt}\frac{\partial L}{\partial\dot x}=0\] \[\frac{GMmx}{\sqrt{x^2+y^2}^3}-\frac{d}{dt}(m\dot x)=0\] \[\frac{GMmx}{\sqrt{x^2+y^2}^3}-m\ddot x=0\] なんと、\(x\)軸方向の運動方程式になる。ラグランジアンの例として \[L(x_i,\dot x_i)=\frac{1}{2}m(\dot x^2+\dot y^2+\dot z^2)-U(x,y,z)\quad (x_i=x,y,z)\] のようにしてもよい。作用\(S(x_i)\)が極値を取るとき、オイラーラグランジュ方程式 \[\frac{\partial L(x_i,\dot x_i)}{\partial x_i}-\frac{d}{dt}\frac{\partial L(x_i,\dot x_i)}{\partial \dot x_i}=0\] は具体的には、 \[-\frac{\partial U(x,y,z)}{\partial x_i}-\frac{d}{dt}(m\dot x_i)=0\] \[m\ddot x_i=-\frac{\partial U(x,y,z)}{\partial x_i}\] \(x_i\)方向の運動方程式になっている。もちろんオイラー・ラグランジュ方程式は、ラグランジアンが\(L(x_i,\dot x_i,t)\)のように時間に陽な関数(\(t\)が\(x\)や\(\dot x\)の中に入っている必要がない。)でもよいので、もうっちょい自由な形を取れる。要するにラグランジアンを工夫して取ることで、摩擦力や、抵抗力を受ける物体の運動みたいな経路もオイラー・ラグランジュ方程式で求められる。

＊＊ラグランジアン＊＊

　例として、ラグランジアン\(L(x_i,\dot x_i)\quad(x_i=x,y,z)\)を運動エネルギーとポテンシャルエネルギーの差 \[L(x_i,\dot x_i):=\frac{1}{2}m(\dot x^2+\dot y^2+\dot z^2)-U(x,y,z)\] で定義することで、\(x_i\)方向のオイラー・ラグランジュ方程式は、\(x_i\)方向の運動方程式 \[m\ddot x_i=-\frac{\partial U(x,y,z)}{\partial x_i}\]

　この記事だけ読むと、今まで解けていた問題をわざわざ経路が分からないふりをして、複数の経路を考えて問題を解くのはちょっと回りくどくみえるか、、、、。