/*　補足　ベクトル３重積

　3つのベクトル\(\boldsymbol{A},\boldsymbol{B},\boldsymbol{C}\)について、 \[\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C})=\begin{pmatrix}A_x\\A_y\\A_y\end{pmatrix}\cdot\begin{pmatrix}B_yC_z-B_zC_y\\B_zC_x-B_xC_z\\B_xC_y-B_yC_x\end{pmatrix}\] \[=A_xB_yC_z+A_yB_zC_x+A_zB_xC_y\] \[-A_xB_zC_y-A_yB_xC_z-A_zB_yC_x\] \[=C_x(A_yB_z-A_zB_y)+C_y(A_zB_x-A_xB_z)+C_z(A_yB_z-A_zB_y)\] \[\begin{pmatrix}C_x\\C_y\\C_y\end{pmatrix}\cdot\begin{pmatrix}A_yB_z-A_zB_y\\A_zB_x-A_xB_z\\A_xB_y-A_yB_x\end{pmatrix}=\boldsymbol{C}\cdot(\boldsymbol{A}\times\boldsymbol{B})\] 平行六面体の底面積が\(|\boldsymbol{B}\times\boldsymbol{C}|\)高さが、\(\boldsymbol{A}\cdot(\boldsymbol{B}\times\boldsymbol{C}/|\boldsymbol{B}\times\boldsymbol{C}|)\)と知ってる人は証明せずとも、\(\boldsymbol{A},\boldsymbol{B}\)が作る平行四辺形を底面とすれば３重積が変わらないことが分かると思う。

終わり　*/

　これも変分法による定理である。ある物理量の微小変化によって、作用\(S\)が変化しなければ、その物理量に対応する保存量があるという定理である。 作用は \[S=\int_{t_0}^{t_1}L(x_i(t),\dot x_i(t),t)dt\] のように表せた。ある物理量の微小変化により、 \[t\mapsto t+\delta t\] \[x_i\mapsto x_i+\delta x_i\] \[\dot x_i\mapsto\dot x_i+\delta\dot x_i\] のように変化したとしよう。\(\delta t\)は時間に依らない小さい定数とする。経路のずれ\(\delta x_i\)は時間によって変化する。ラグランジアンは、 \[L(x_i+\delta x_i,\dot x_i+\delta\dot x_i,t+\delta t)\] \[\simeq L+\frac{\partial L}{\partial x_i}\delta x_i+\frac{\partial L}{\partial\dot x_i}\delta\dot x_i+\frac{\partial L}{\partial t}\delta t\] であるから、 \[\delta S=\int_{t_0}^{t_1}L(x_i(t),\dot x_i(t),t)dt\] \[\delta S=\int_{t_0}^{t_1}\left(\frac{\partial L}{\partial x_i}\delta x_i+\frac{\partial L}{\partial\dot x_i}\delta\dot x_i+\frac{\partial L}{\partial t}\delta t\right)dt\tag{1}\] 作用が変化しないという仮定からオイラー・ラグランジュ方程式 \[\frac{\partial L}{\partial x_i}-\frac{d}{dt}\frac{\partial L}{\partial\dot x_i}=0\] を使うことができる。(1)式の１項目に使用すると、 \[\delta S=\int_{t_0}^{t_1}\left(\frac{d}{dt}\frac{\partial L}{\partial\dot x_i}\delta x_i+\frac{\partial L}{\partial\dot x_i}\delta\dot x_i+\frac{\partial L}{\partial t}\delta t\right)dt\] \[\delta S=\int_{t_0}^{t_1}\left(\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}\delta x_i\right)+\frac{\partial L}{\partial t}\delta t\right)dt\tag{2}\] ３項目の\(\partial L/\partial t\)を求めるためラグランジアンの時間微分を計算する。 \[\frac{dL(x_i,\dot x_i,t)}{dt}=\frac{\partial L}{\partial x_i}\dot x_i+\frac{\partial L}{\partial\dot x_i}\frac{d\dot x_i}{dt}+\frac{\partial L}{\partial t}\] こちらも１項目にオイラー・ラグランジュ方程式を使う。 \[\frac{dL}{dt}=\frac{d}{dt}\frac{\partial L}{\partial\dot x_i}\dot x_i+\frac{\partial L}{\partial\dot x_i}\frac{d\dot x_i}{dt}+\frac{\partial L}{\partial t}\] 順番を入れ替えて \[\frac{\partial L}{\partial t}=\frac{dL}{dt}-\frac{d}{dt}\frac{\partial L}{\partial\dot x_i}\frac{dx_i}{dt}-\frac{\partial L}{\partial\dot x_i}\frac{d\dot x_i}{dt}\] \[\frac{\partial L}{\partial t}=\frac{d}{dt}\left(L-\frac{\partial L}{\partial\dot x_i}\dot x_i\right)\] これを(2)式に代入して、 \[\delta S=\int_{t_0}^{t_1}\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}\delta x_i-\left(\frac{\partial L}{\partial\dot x_i}\dot x_i-L\right)\delta t\right)dt\tag{3}\] これが得たかった式である。

　時間を少しだけ動かすことを考える、とても小さい時間\(\tau\)を使って、\(\delta x_i=0,\delta t=\tau\)とすればよいので、(3)式は \[\delta S=\int_{t_0}^{t_1}-\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}\dot x_i-L\right)\tau dt=0\] \(\delta S=0\)の条件は\(\tau\neq0\)なので、 \[\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}\dot x_i-L\right)=0\] でなければならない。つまり \[\frac{\partial L}{\partial\dot x_i}\dot x_i-L=const.\] ラグランジアンを\(L=m\dot x_i^2/2-U(x_i)\)と取れば、 \[\frac{1}{2}m\dot x_i^2+U(x_i)=const.\] 時間発展対称性は、エネルギーの保存を表していることが分かる。

　空間を少しだけ進むことを考える。とても小さい変位\(a_i\)を使って、\(\delta x_i=a_i,\delta t=0\)とすればよいので、 \[\delta S=\int_{t_0}^{t_1}\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}a_i\right)dt=0\] ラグランジアンを\(L=m\dot x_i^2/2-U(x_i)\)と取れば、 \[\frac{\partial L}{\partial\dot x_i}=m\dot x_i=p_i\] かっこの中は運動量と並進ベクトルの内積であることが分かる。\(\delta S=0\)の条件は \[\frac{d(p_ia_i)}{dt}=\frac{d(\boldsymbol{p}\cdot\boldsymbol{a})}{dt}=\frac{d\boldsymbol{p}}{dt}\cdot\boldsymbol{a}=0\] \(a_i\neq0\)なので、 \[\boldsymbol{p}=\boldsymbol{const.}\] 空間並進対称性は、運動量の保存を表していることが分かる。

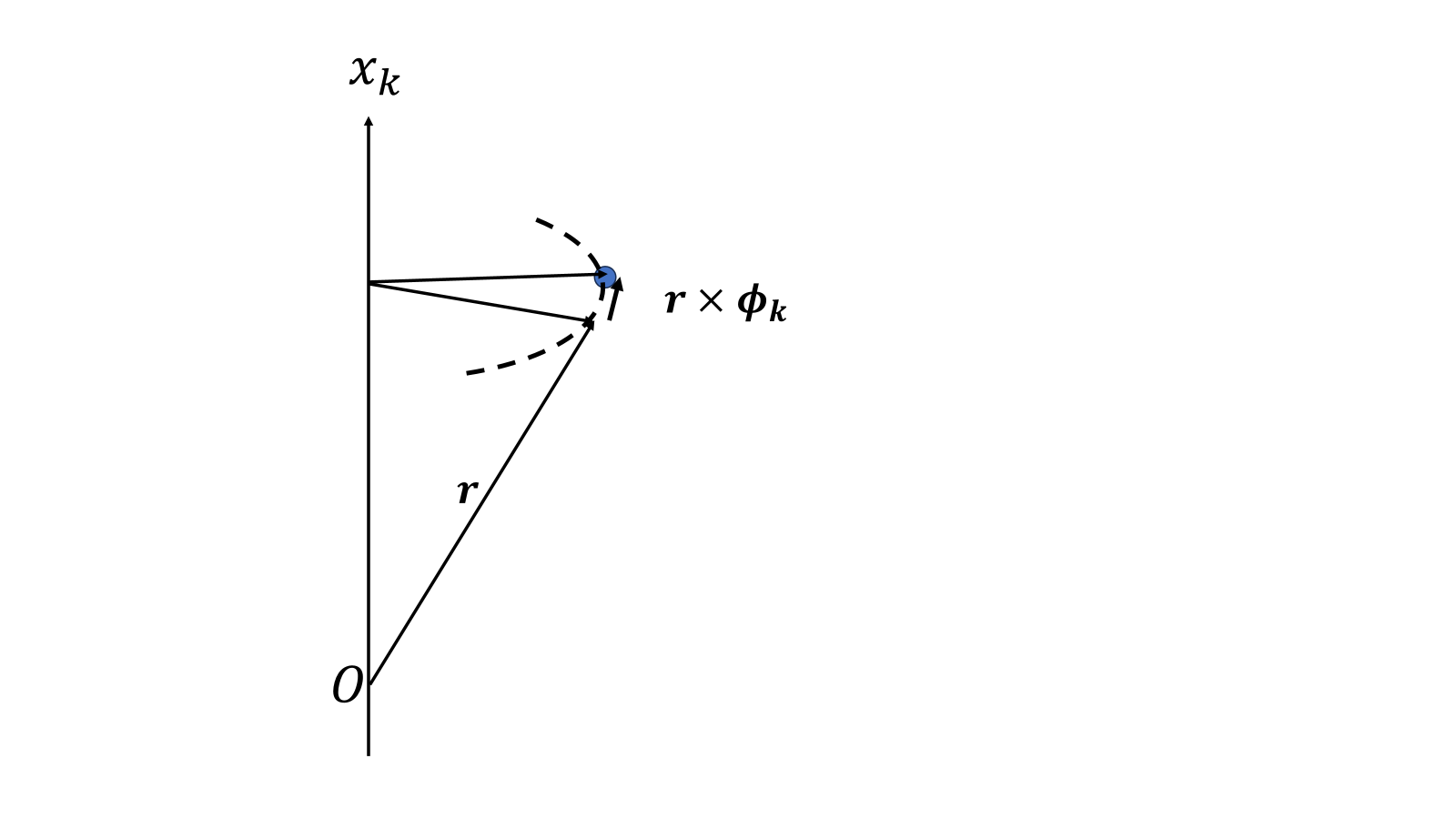
　空間回転は外積を使うと楽なので、ベクトルを使って示すと、とても小さいベクトル\(\boldsymbol{\phi}\)を使って\(\delta \boldsymbol{x}=\boldsymbol{r\times\phi}\)とあらわす。 \[\delta S=\int_{t_0}^{t_1}\frac{d}{dt}\left(\frac{\partial L}{\partial\dot x_i}\delta x_i\right)dt=0\] \[\delta S=\int_{t_0}^{t_1}\frac{d}{dt}\left(p_i\delta x_i\right)dt=0\] つまり \[\frac{d}{dt}\left(p_i\delta x_i\right)=\frac{d}{dt}\left(\boldsymbol{p}\cdot(\boldsymbol{r}\times\boldsymbol{\phi})\right)=0\] \[-\frac{d}{dt}(\boldsymbol{r}\times\boldsymbol{p})\cdot\boldsymbol{\phi}=0\] \(\phi\neq0\)なので、 \[\boldsymbol{r}\times\boldsymbol{p}=\boldsymbol{const.}\] でなければならない。

＊＊ネーターの定理＊＊

　ある物理量の変化によって、作用\(S\)が変化しなければその物理量に対応する保存則がある。 の保存則が対応する。

　この定理すごくないですか！私が好きな定理です。保存則がまとめて１つの定理で説明できるのはすごいですね。どのような視点で、この定理を見つけたのやら。あまり複雑な系は好きでないので１物体系についてやってますが、3つの保存則は複数の物体系でも成り立ちます。もともとこれらの法則は力の種類により分類されていました。保存力なら力学的エネルギー保存の法則、外力が０なら運動量保存、向心力なら角運動量の保存といったものです。しかしネーターの定理は、時間に対する対称性、空間に対する対称性、向きに対する対称性という新しい視点を与えてくれます。