楽しい科学（理論）チャンネル

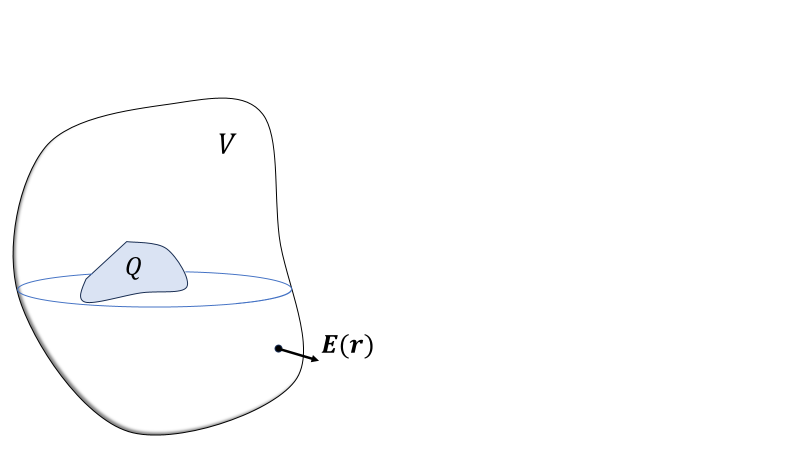
　図のような任意の領域\(V\)に囲まれた大きさのある電荷\(Q\)がある。(電位の\(V\)とか、電位の単位の\(\mathrm{V}\)とか、空間上の領域\(V\)とか同じ文字が多くて申し訳ない。ここでは電位の話はしないので、全部体積の\(V\)ということでお願いします！このページでは領域と体積や、曲面と面積の記号が混同していますが、記号を増やすとみずらいのでご容赦ください。) 領域\(V\)の表面\(\partial V\)上の電場\(\boldsymbol{E}(\boldsymbol{r})\)と電荷\(Q\)についての関係を求めたい。本題のガウスの法則である。

電荷\(Q\)を点電荷とみなせるくらい小さい要素\(Q_{\alpha}\)に分ける。\(Q_{\alpha}\)の作る電場\(\boldsymbol{E}_{\alpha}\)は \[\boldsymbol{E}_{\alpha}(\boldsymbol{r})=\frac{kQ_{\alpha}}{|\boldsymbol{r}-\boldsymbol{r}_{\alpha}|^2}\frac{\boldsymbol{r}-\boldsymbol{r}_{\alpha}}{|\boldsymbol{r}-\boldsymbol{r}_{\alpha}|}\] 見通しが悪いので\(\boldsymbol{r}-\boldsymbol{r}_{\alpha}=\boldsymbol{R}\)と置き換える。\(\partial V\)の閉曲面で面積分する。 \[\iint_{\partial V}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=\iint_{\partial V}\frac{kQ_{\alpha}}{R^2}\hat{\boldsymbol{R}}\cdot d\boldsymbol{S}\] ここでガウスの定理\(\iiint_{V}\nabla\cdot\boldsymbol{E}dV=\iint_{\partial V}\boldsymbol{E}\cdot d\boldsymbol{S}\)を使う。更に\(Q_{\alpha}\)を中心とする半径\(\varepsilon\)の球\(V_{\varepsilon}\)を用いる。\(V\)から\(V_{\varepsilon}\)をくり抜いた立体を\(V-V_{\varepsilon}\)とする。 \[\iint_{\partial V}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=kQ_{\alpha}\iiint_{V}\nabla\cdot\frac{\hat{\boldsymbol{R}}}{R^2}dV\] \[=kQ_{\alpha}\iiint_{V-V_{\varepsilon}}\nabla\cdot\frac{\hat{\boldsymbol{R}}}{R^2}dV+kQ_{\alpha}\iiint_{V_{\varepsilon}}\nabla\cdot\frac{\hat{\boldsymbol{R}}}{R^2}dV\tag{1}\] (1)式の第１項目を解くために\(\nabla\cdot(\hat{\boldsymbol{R}}/R^2)=\nabla\cdot(\boldsymbol{R}/R^3)\)を計算してみる。\(\boldsymbol{R}=\boldsymbol{0}\)となるのは\(V_{\varepsilon}\)に含まれるので\(V-V_{\varepsilon}\)の領域では常に\(\boldsymbol{R}\neq\boldsymbol{0}\)である。 \[\frac{\partial}{\partial x}\hat{\boldsymbol{x}}\cdot\frac{\hat{\boldsymbol{R}}}{R^2}=\frac{\partial}{\partial x}\hat{\boldsymbol{x}}\cdot\frac{(x-x_{\alpha})\hat{\boldsymbol{x}}+(y-y_{\alpha})\hat{\boldsymbol{y}}+(z-z_{\alpha})\hat{\boldsymbol{z}}}{\sqrt{(x-x_{\alpha})^2+(y-y_{\alpha})^2+(z-z_{\alpha})^2}^3}\] \[=\frac{(x-x_{\alpha})^2+(y-y_{\alpha})^2+(z-z_{\alpha})^2-3(x-x_{\alpha})^2}{\sqrt{(x-x_{\alpha})^2+(y-y_{\alpha})^2+(z-z_{\alpha})^2}^4}\] \(y,z\)成分についても同じように計算すると、\(\boldsymbol{R}\neq\boldsymbol{0}\)のとき \[\nabla\cdot\frac{\hat{\boldsymbol{R}}}{R^2}=\frac{\partial}{\partial x}\hat{\boldsymbol{x}}\cdot\frac{\hat{\boldsymbol{R}}}{R^2}+\frac{\partial}{\partial x}\hat{\boldsymbol{y}}\cdot\frac{\hat{\boldsymbol{R}}}{R^2}+\frac{\partial}{\partial x}\hat{\boldsymbol{z}}\cdot\frac{\hat{\boldsymbol{R}}}{R^2}=0\] (1)式第１項目は\(0\)となる。第２項目にもう一度ガウスの定理を使う。単位面積要素ベクトルを\(\boldsymbol{n}\)とすると、球面\(\partial V_{\varepsilon}\)と\(\hat{\boldsymbol{R}}\)は常に垂直である。つまり球面\(\partial V_{\varepsilon}\)の法線ベクトル\(\boldsymbol{n}\)と\(\hat{\boldsymbol{R}}\)は平行であので内積は\(\boldsymbol{n}\cdot\hat{\boldsymbol{R}}=1\)であるから \[kQ_{\alpha}\iiint_{V_{\varepsilon}}\nabla\cdot\frac{\hat{\boldsymbol{R}}}{R^2}dV=kQ_{\alpha}\iint_{\partial V_{\varepsilon}}\frac{\hat{\boldsymbol{R}}}{R^2}\cdot d\boldsymbol{S}\] \[=kQ_{\alpha}\iint_{\partial V_{\varepsilon}}\frac{\hat{\boldsymbol{R}}\cdot \boldsymbol{n}}{R^2}dS=kQ_{\alpha}\iint_{\partial V_{\varepsilon}}\frac{dS}{R^2}\] 常に\(R=\varepsilon\)かつ、\(\partial V_{\varepsilon}=4\pi\varepsilon^2\)なので、(1)式は \[\iint_{\partial V}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=kQ_{\alpha}\iiint_{V-V_{\varepsilon}}0dV+\frac{kQ_{\alpha}}{\varepsilon^2}\iint_{4\pi\varepsilon^2}dS\] \[\iint_{\partial V}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=4\pi kQ_{\alpha}\] 計算のため電荷\(Q\)を\(Q_{\alpha}\)に分けたのであった。電荷\(Q_\alpha\)、電場\(\boldsymbol{E}_\alpha\)を足し合わせると、 \[\sum_{\alpha}\iint_{\partial V}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=\sum_{\alpha}4\pi kQ_{\alpha}\] \[\iint_{\partial V}\sum_{\alpha}\boldsymbol{E}_{\alpha}(\boldsymbol{r})\cdot d\boldsymbol{S}=\sum_{\alpha}4\pi kQ_{\alpha}\] \[\iint_{\partial V}\boldsymbol{E}(\boldsymbol{r})\cdot d\boldsymbol{S}=4\pi kQ\] 電荷\(Q\)と電場\(\boldsymbol{E}\)の関係を１つの式で表すことができた！係数をまとめて\(4\pi k=1/\epsilon_0\)とすると、 \[\iint_{\partial V}\epsilon_0\boldsymbol{E}(\boldsymbol{r})\cdot d\boldsymbol{S}=Q\] \(\epsilon_0\)は真空中の誘電率であり単位はクーロン係数の逆数なので、\(\mathrm{kg^{-1}\ m^{-3}\ s^{4}\ A^{2}}\)である。ところで電場\(\boldsymbol{E}\)の単位は\(\mathrm{kg\ m\ s^{-3}\ A^{-1}}\)であった。電束密度\(\boldsymbol{D}:=\epsilon_0\boldsymbol{E}\)を定義すると、その単位は、\(\mathrm{A\ s\ m^{-2}=C\ m^{-2}}\)とすっきりした単位で表せる。さらにガウスの法則により閉曲面で面積分すると、その領域内にある電荷が求まる。単位だけ見ると電荷の面密度に見えるがそうではない。

＊＊ガウスの法則(電気)＊＊

領域\(V\)の表面\(\partial V\)での電束密度\(\boldsymbol{D}(\boldsymbol{r}),(\boldsymbol{r}\in\partial V)\)の面積分は領域にある電荷\(Q\)に等しい。 \[\iint_{\partial V}\boldsymbol{D}(\boldsymbol{r})\cdot d\boldsymbol{S}=Q\]

とても有名式ですな。ガウスの法則である。これを導く途中式でもガウスの定理というものを使った。ガウス様様だぜ。媒質中や電荷が領域からはみ出ていている場合の計算方法もある。今回は真空中という定で進めてきたが、過程はできるだけシンプルなほうが本質が見えると思う。

　磁石同士にも力がはたらく。N極を(＋)、S極を(-)の磁荷\(m\)を持つものとする。N極だけ、S極だけの磁荷は見つかっていない。(棒磁石を半分に割ると2つのS極N極を持つ磁石になってしまうのだ。)電気に対して磁気の式が理解しずらいのは磁荷がない為だと僕は思う。というわけで始めに磁荷を使って磁気の式を導いて最後に磁荷を消し去る。というわけでこれからの話は嘘である。とはいえ、磁石が受ける力を考えるときには有効な話ではある。磁荷を仮定することで電気のと同じ式で磁気が扱える。

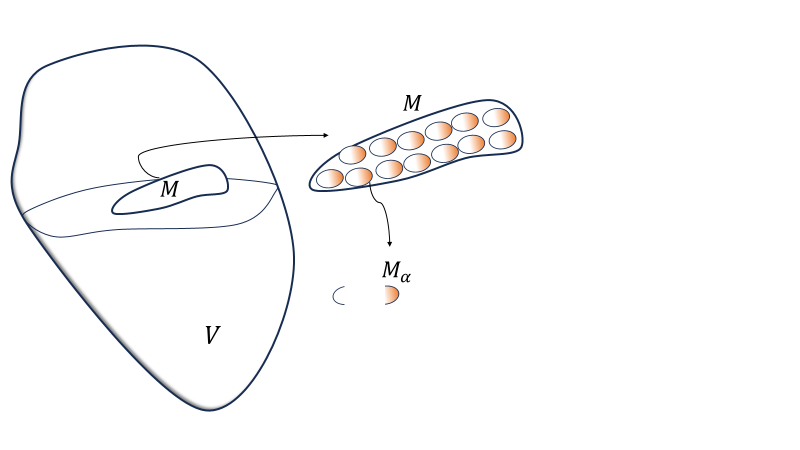
　電場のときと同様に領域\(V\)の表面上\(\partial V\)で\(M\)が作る磁場\(\boldsymbol{H}(\boldsymbol{r})\)の面積分は \[\iint_{\partial V}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}=4\pi k_mM\] と表すことができる。透磁率\(\mu_0=1/4\pi k_m\)、\([\mu_0]=\mathrm{N^{-1}\ m^{-2}\ Wb^{2}}\)とすると、 \[\iint_{\partial V}\mu_0\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}=M\] 磁荷\(M\)を細かく分割した要素\(M_\alpha\)とするとその分割の中で\(M_\alpha\)と磁荷の大きさが同じで符号が逆のペアがあるので、\(M=\sum M_\alpha=0\)である。磁束密度\(\boldsymbol{B}:=\mu_0\boldsymbol{H}\)を定義すると \[\iint_{\partial V}\boldsymbol{B}(\boldsymbol{r})\cdot d\boldsymbol{S}=0\] 磁束密度の単位は\(\mathrm{Wb\ m^{-2}}\)である。

＊＊ガウスの法則(磁気)＊＊

　領域\(V\)の表面\(\partial V\)での磁束密度\(\boldsymbol{B}(\boldsymbol{r}),(\boldsymbol{r}\in\partial V)\)の面積分は0になる。 \[\iint_{\partial V}\boldsymbol{B}(\boldsymbol{r})\cdot d\boldsymbol{S}=0\]

今回はガウスの法則について説明した。電気量の単位\(\mathrm{C}\)、磁気量の単位\(\mathrm{Wb}\)の関係性は次回。ちょっとだけ詳しい話をすると、電荷を持つ物質が存在するのは電子という電荷を付与する粒子が摩擦などで簡単に移動するためである。電子を受け取った物質は負の電荷を帯びて、電子を渡した物質は正の電荷を帯びる。一方で磁荷が無いのは物質間で磁気量を移動する方法がないためであり、磁力を帯びるためには同じ物質間で分極(一部が磁気を帯びて他の部分が逆の符号の磁気を帯びる)方法しかないためである。もし磁荷が見つかったら今回の話も意味があるラッキー！