楽しい科学（理論）チャンネル

　まずはファラデーの法則、アンペールの法則を理解するための基本知識を書いていく。

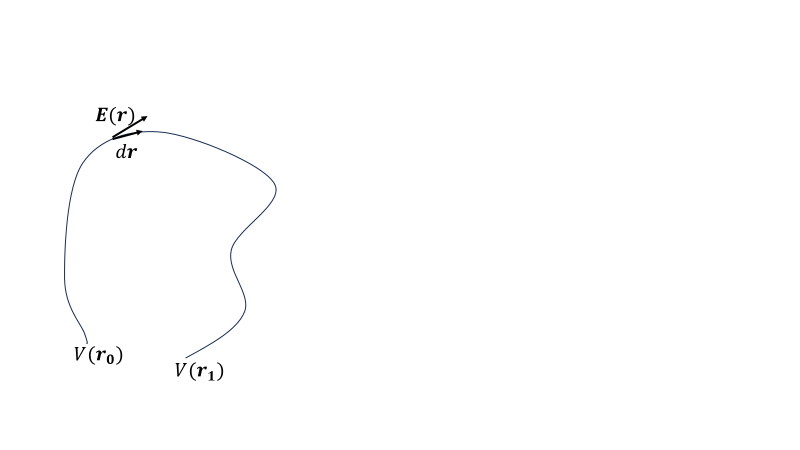
直流電流装置\(\varDelta V\)についてもう少し詳しく述べると、図のような経路での電場\(\boldsymbol{E}(\boldsymbol{r})\)の線積分は、 \[V(\boldsymbol{r_1})-V(\boldsymbol{r_0})=\int_{\boldsymbol{r_0}}^{\boldsymbol{r_1}}-\boldsymbol{E}(\boldsymbol{r})\cdot d\boldsymbol{r}\] とあらわせる。電圧\(\varDelta V\)とは電位差であるので、直流電源\(\varDelta V\)は \[\varDelta V=\int_{\boldsymbol{r_0}}^{\boldsymbol{r_1}}-\boldsymbol{E}_I(\boldsymbol{r})\cdot d\boldsymbol{r}\] とも表現できる。後に説明するコンデンサーのような回路が途中で切れていて電流で表現ができない部分で有効な書き方だ。この\(\boldsymbol{E}_I\)はケーブル中の電場である。ケーブル中の電荷\(Q\)について\(I=dQ/dt\)の流速で、電気量\(Q\)が入ってきて、終点から\(Q\)出ていく。ケーブルは帯電しているわけではない。後に詳しく述べたい。 準備はできた。まずはアンペールの法則！

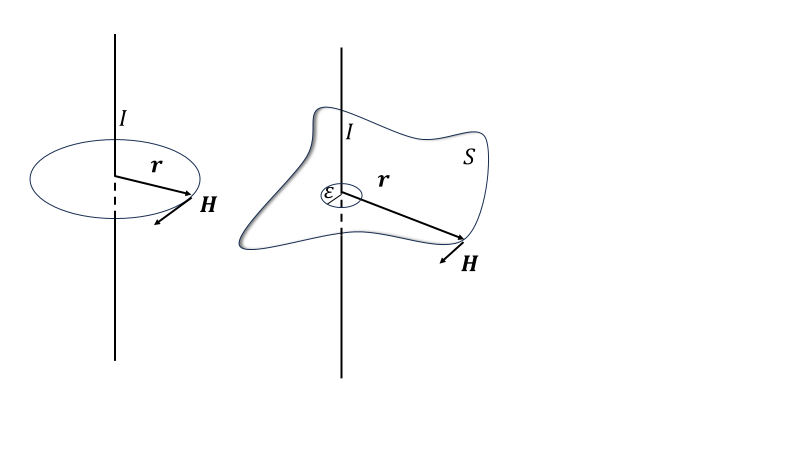
図の左側ように直線に流れる電流\(I\)があるとき、直線から距離\(r\)だけ離れた点での磁場の大きさは\(H=I/2\pi r\)であり、右ねじの方向であることが実験により確かめられた。

＊＊アンペールの法則＊＊

直線電流\(I\)があるとき直線との距離\(r\)での磁場の大きさは \[H=\frac{I}{2\pi r}\]

この法則により磁場の単位は\(\mathrm{N\ Wb^{-1}}\)であるから、\[\mathrm{N\ Wb^{-1}=A\ m^{-1},\ Wb=kg\ m^2\ s^{-2}\ A^{-1}}\] アンペールの法則を任意の曲面\(S\)の周で磁場\(\boldsymbol{H}(\boldsymbol{r})\)積分したものが曲面を貫く電流\(I\)であることを示すことができる。電流が曲面\(S\)を貫く点で接する半径\(\varepsilon\)の小さい円を\(s\)とする。(電流が貫く点近傍で\(S\)が平面とみなせるくらい小さい円)まずはストークスの定理\(\int_{\partial S}\boldsymbol{H}\cdot d\boldsymbol{r}=\iint_{S}\nabla\times\boldsymbol{H}\cdot d\boldsymbol{S}\)を使い、 \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}\] \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S-s}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}+\iint_{s}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}\] この式の第1項目を求めるため、\(\nabla\times\boldsymbol{H}(\boldsymbol{r}),\ \boldsymbol{r}\neq\boldsymbol{0}\)の\(z\)成分を求める。簡単にするため、電流の方向を\(z\)軸にとる。磁場\(\boldsymbol{H}(\boldsymbol{r})\)は電流に対して右ねじ方向つまり\(\boldsymbol{r}=\boldsymbol{x}+\boldsymbol{y}\)と垂直なので、 \[\frac{\boldsymbol{H}}{|\boldsymbol{H}|}\cdot\boldsymbol{r}=\ \frac{H_x}{|H|}x+\frac{H_y}{|H|}y=0,\ H=\frac{I}{2\pi r}\] を満たすように \[\boldsymbol{H}(\boldsymbol{r})=\frac{Iy}{2\pi(x^2+y^2)}\hat{\boldsymbol{x}}-\frac{Ix}{2\pi(x^2+y^2)}\hat{\boldsymbol{y}}\] とでも書こうか。(\(x,y\)成分で符号が逆になっていれば、今回はどちらが―でも条件は満たすため\(y\)成分を―にした。) \(\nabla\times\boldsymbol{H}(\boldsymbol{r})\)は\(z\)方向のみなので、 \[[\nabla\times\boldsymbol{H}(\boldsymbol{r})]_z=\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial y}\] \[=\frac{I(x^2+y^2-2x^2)}{2\pi(x^2+y^2)^2}+\frac{I(x^2+y^2-2y^2)}{2\pi(x^2+y^2)^2}=0\] 積分の中身が0なので１項目は0、２項目を計算する。 \[\iint_{s}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{s}=\int_{\partial s}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}\] \(\partial s\)は半径\(\varepsilon\)周であるので\(\partial s=2\pi \varepsilon\)磁場\(\boldsymbol{H}\)と線素ベクトル\(d\boldsymbol{r}\)は常に同じ方向なので(磁場は右ねじの方向) \[\int_{\partial s}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\int_{\partial s}Hdr=\int_{\partial s}\frac{I}{2\pi \varepsilon}dr=\frac{I}{2\pi \varepsilon}2\pi\varepsilon\] \[\iint_{s}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{s}=I\] 以上から \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S-s}\boldsymbol{0}\cdot d\boldsymbol{S}+\iint_{s}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{S}\] \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=I\] 電流密度\(\boldsymbol{j}\)を使って表すと、 \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S}\boldsymbol{j}(\boldsymbol{r})\cdot d\boldsymbol{S}\] となる。

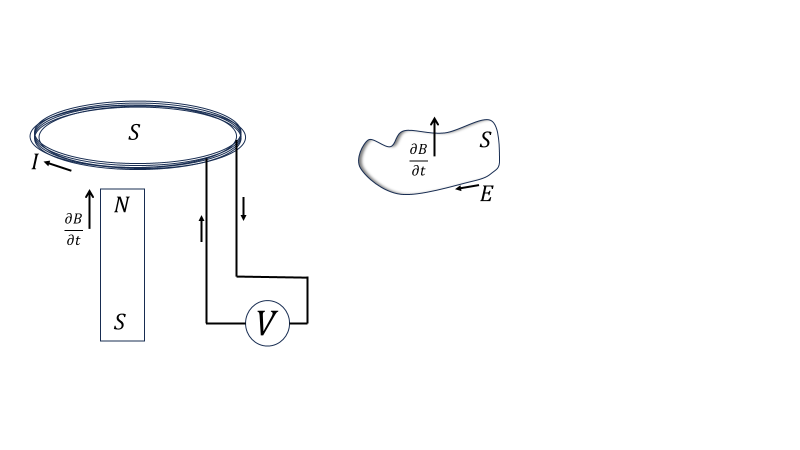
はじめに、磁束\(\Phi\)を \[\Phi:=\iint_{S}\boldsymbol{B}\cdot d\boldsymbol{S}\] で定義する。 よく見る電磁誘導の図(レンツの法則で用いられる装置)である。実際ファラデーはコイルに鉄心を差し込んで、その鉄心を磁石で磁化させて実験を行っていた。この記事でもこれを使って説明したい。図のように\(n\)回巻いたコイルと電圧計をつないだ装置がある。この装置の近くで磁石を動かしたとき電圧計の針が振れる。磁束\(\Phi\)の時間変化(磁石を動かす。)と電圧\(\varDelta V\)が比例するということが判明した。また同じ磁束\(\Phi\)の場合、巻き数が多いほうが電圧が大きいことも実験により確かめられた。

＊＊ファラデーの法則＊＊

巻き数\(n\)のコイルがあり、コイルの内部の面を\(S\)とすると、面\(S\)を貫く磁束\(\Phi\)が時間変化すると電圧\(\varDelta V\)が生じる。 \[\varDelta V=-n\frac{\partial\Phi(t)}{\partial t}\]

符号が負になっているのは、磁束\(\Phi\)の時間変化の「逆」右ねじの方向に起電力が発生するためである。 １回巻きの場合、\(\varDelta V=-\partial\Phi/\partial t\)であるため電磁誘導(ファラデーの法則)は、コイルを周とする面\(S\)を考えると、 \[\int_{\partial S}\boldsymbol{E}_I(\boldsymbol{r},t)\cdot d\boldsymbol{r}=-\frac{\partial}{\partial t}\iint_{S}\boldsymbol{B}(\boldsymbol{r},t)\cdot d\boldsymbol{S}\tag{1}\] とかける。アンペールの法則のように任意の曲面について言えたわけではない。しかしアンペールの法則では電流から磁場が生じ、ファラデーの法則では磁束の時間変化から起電力(電流)が生じるという電気と磁気が対称的な存在であることが示されたことが大切である。

電磁気学の基礎となる方程式について説明してきたのでその応用として、コンデンサー、ソレノイドについて説明しよう。 まず図のような、電気量\(Q\)に帯電した板\(S\)(理想的には無限に広い板)があるとしよう。電荷面密度は\(\sigma=Q/S\)とする。そこに表面積\(6A\)の立方体領域\(V\)を図のように取る。位置ベクトル\(\boldsymbol{r}\)を用いて表面上\(\partial V\)の電場を\(\boldsymbol{E}(\boldsymbol{r})\)と表す。面のある点\(\alpha\)が作る位置\(\boldsymbol{r}\)が作る電場を\(\boldsymbol{E}_{\alpha}(\boldsymbol{r})\)、\(S\)に垂直な軸\(l\)で対称な点\(\alpha'\)が作る電場を\(\boldsymbol{E}_{\alpha'}(\boldsymbol{r})\)とすると、面\(S\)平行な成分は相殺して、垂直な成分のみ残る。よって\(\boldsymbol{E}(\boldsymbol{r})=\sum\boldsymbol{E}_{\alpha}(\boldsymbol{r})\)も面\(S\)に垂直である。領域\(V\)の板\(S\)に垂直な面では、電場と面積要素の内積は\(0\)面\(S\)と面積要素ベクトルと電場が平行な2面については平行な成分は\(\boldsymbol{E}(\boldsymbol{r})\cdot\boldsymbol{A}=EA\)となる。ガウスの法則を領域\(V\)に使うと、 \[\iint_{6A}\epsilon_0\boldsymbol{E}(\boldsymbol{r})\cdot d\boldsymbol{s}=2\epsilon_0EA\] 領域内の電荷は\(\sigma A\)なので、面積要素単位ベクトル\(\boldsymbol{n}\)を用いて、 \[2\epsilon_0 EA=\sigma A,\ \boldsymbol{E}=\frac{\sigma}{2\epsilon_0}\boldsymbol{n}\] なんと面電荷が作る電場は離れても、面との距離に依らず一定なのか！

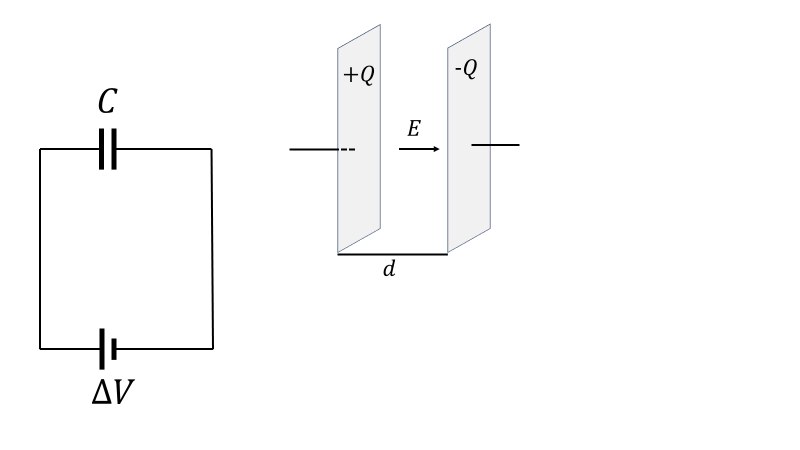
これがコンデンサーという装置だ。(簡単にするため極板間は真空とする。)電荷を蓄えるための装置で板を２枚近づけただけ。電流が流れると図のような配置だと、右の極板に正の電荷、左の極板に負の電荷を蓄える。コンデンサー内で電場\(\boldsymbol{E}\)は、左右の極板からの電場の和になるので、 \[\boldsymbol{E}=\frac{\sigma}{2\epsilon_0}\boldsymbol{n}+\frac{-\sigma}{2\epsilon_0}(-\boldsymbol{n})=\frac{\sigma}{\epsilon_0}\boldsymbol{n}=\frac{Q}{\epsilon_0A}\boldsymbol{n}\] コンデンサーの電圧は、 \[V_C=\int_0^d\boldsymbol{E}\cdot d\boldsymbol{x}=Ed=\frac{Qd}{\epsilon_0A}\] 電圧と、コンデンサーが蓄えている電荷は比例関係にあるようだ。静電容量\(C:=\epsilon_0A/d\)とすると、 \[Q=CV_C\] この式、静電容量の定義から、コンデンサーはより極板が近く、極板の面積が大きいほど、多くの電荷を貯蔵できることがわかる。

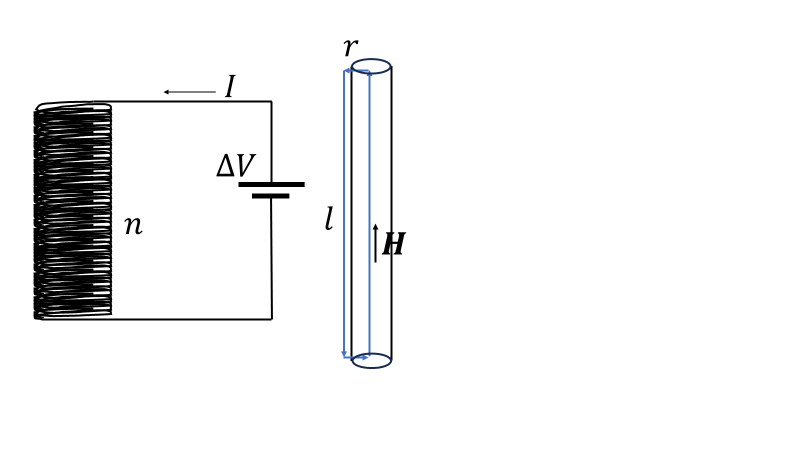
続いてこちらがソレノイドである。コイルを\(n\)回巻いたものである。右側が理想的なソレノイドで、側面は隙間がなくコイルがぎっしり詰まっているものである。(できれば無限に長いもの。)では長さ\(l\)ソレノイドと電流の関係を求めたい。ソレノイドに辺の長さが\(l,r\)の長方形の領域\(S\)を図のようにとりアンペールの法則を使う。おおざっぱな計算になるが、\(l\gt\gt r\)、ソレノイドの外の磁場は内部の磁場に比べて無視できるくらい小さいものとする。 \[\int_{\partial S}\boldsymbol{H}\cdot d\boldsymbol{l}=Hl+Hr+H_{out}l+Hr\simeq Hl\] \(n\)回巻いてあるので、領域\(S\)を貫く電流の数も\(n\)個のはずである。 \[Hl=nI,\ H=\frac{n}{l}I\] ソレノイドは長さ辺りの巻き数\(n/l\)を大きくすることで、より大きな磁場が作れることがわかる。ソレノイドの磁束密度\(B\)は\(B=\mu_0H\)、ソレノイドの図でいう上からみた断面積を\(A\)とすると、磁束\(\Phi\)は\(\Phi=BA\)であるから、ファラデーの法則から誘電起電力\(V_L\)を求めることができる。 \[V_L=-n\frac{\partial \Phi}{\partial t}=-\frac{n^2A}{l}\frac{dI}{dt}\] インダクタンス\(L:=n^2A/l\)を定義すると、 \[V_L=-L\frac{dI}{dt}\] なんとソレノイドに電流を流すと、電流と逆向きの起電力\(V_L\)がはたらくようだ。面白い。