楽しい科学（理論）チャンネル

今回は直流、交流の電気回路で、電気抵抗\(R\)、ソレノイド\(L\)、コンデンサー\(C\)を扱う。電気回路に使うケーブルも物質なので、電気抵抗がある。そのためどの回路にも電気抵抗を付けて議論していく。それぞれの回路の電流を求めていく。

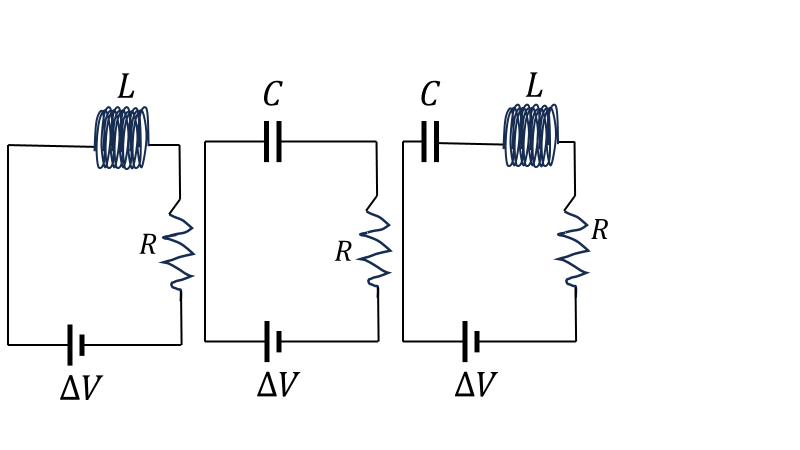
まずは直流電流で、一番左の回路は \[\varDelta V=V_R+V_L\] \[RI-L\frac{dI}{dt}-\varDelta V=0,\ \frac{dI}{dt}-\frac{L}{R}I-\frac{\varDelta V}{R}=0\] \(X=I-\frac{\varDelta V}{L}\)とおくと、 \[\frac{dX}{dt}-\frac{L}{R}X=0,\ X=C_1e^{\frac{L}{R}t}\] 以上から、 \[I=C_1e^{\frac{L}{R}t}+\frac{\varDelta V}{L}\] 真ん中の回路は \[\varDelta V=V_R+V_C,\ \varDelta V=RI+\frac{Q}{C}\] 両辺を時間で微分し\(R\)で割ると、 \[\frac{dI}{dt}+\frac{1}{RC}I=0\] \[I=C_1e^{-\frac{1}{RC}t}\]

\(RL\)回路はソレノイドの磁場が作る逆起電力で始めは、電流が小さいが、増加する指数関数の増え方をする。(実際は電流が極端に大きくなると、電気抵抗がジュール熱を発して電流が無限に大きくなることはない。)\(RC\)回路は時間が経つにつれコンデンサーが電荷を蓄えられなくなって電流は減衰する。 直流の\(RLC\)回路は複雑である。 \[\varDelta V=V_R+V_C+V_L,\ \varDelta V=RI+\frac{1}{C}Q-L\frac{dI}{dt}\] 両辺を時間で微分して整理すると、 \[L\frac{d^2I}{dt^2}-R\frac{dI}{dt}-\frac{1}{C}I=0\] 解を\(I=e^{\lambda t}\)と仮定すると、 \[L\lambda^2-R\lambda-\frac{1}{C}=0,\ \lambda=\frac{-R\pm\sqrt{R^2-4\frac{L}{C}}}{2L}\] 場合分けが必要になってしまった。\(R^2-4\frac{L}{C}\gt 0\)の場合、 \[I=e^{\frac{-R}{2L}t}(C_1e^{\frac{\sqrt{R^2-4L/C}}{2L}t}+C_2e^{\frac{-\sqrt{R^2-4L/C}}{2L}t})\] \(R^2-4\frac{L}{C}\lt 0\)の場合、 \[I=C_1e^{\frac{-R}{2L}t}\cos\left(\frac{\sqrt{R^2-4L/C}}{2L}t+C_2\right)\]

電気抵抗\(R\)が大きい場合は減衰して電流は0に落ち着く。\(R\)の値がある程度小さい場合は、振動しながら減衰する。今回2パターンでしか場合分けしなかったが、積分定数の符号も考えると、いろいろなパターンがありそうだ。

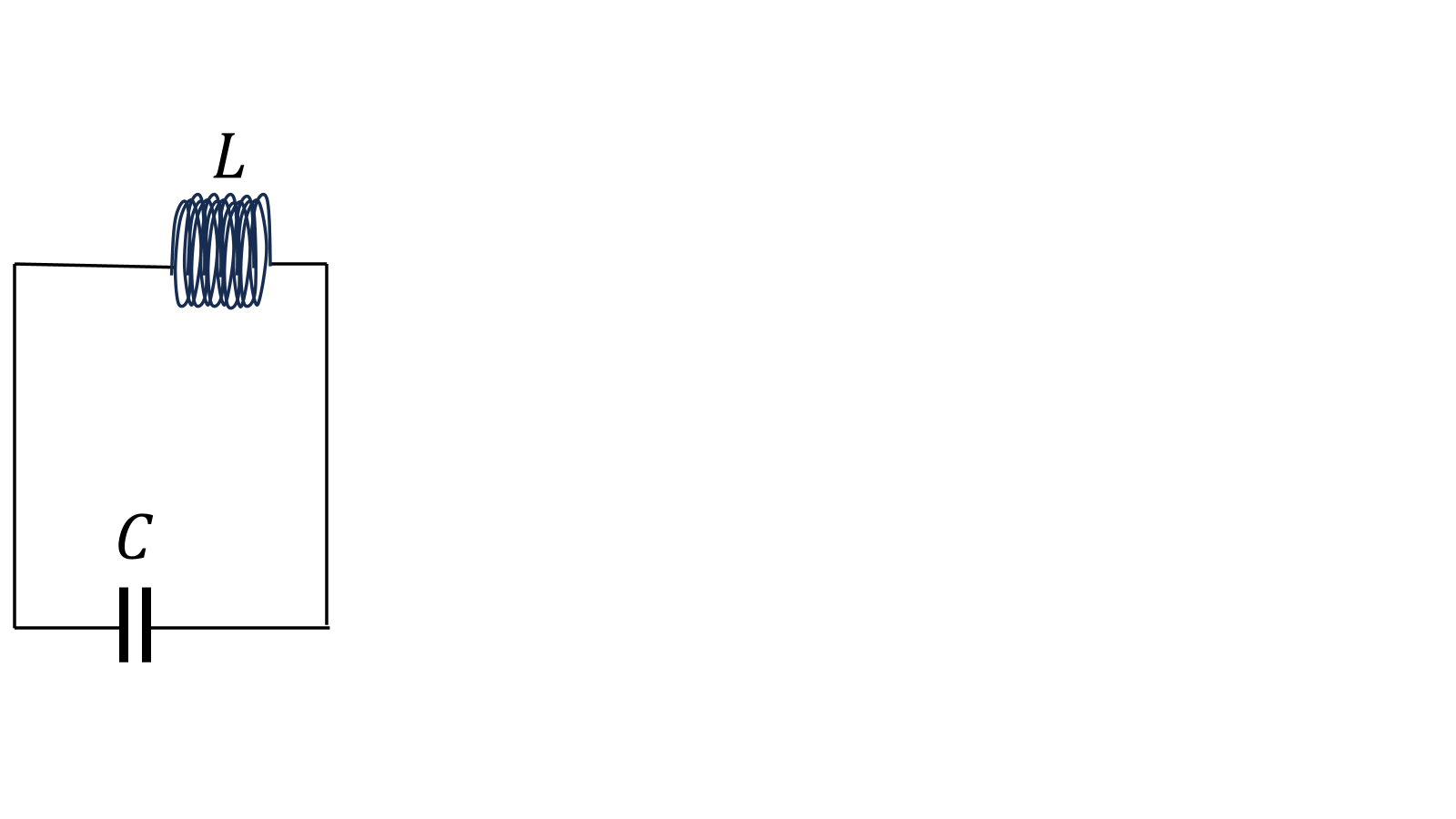
蓄電されたコンデンサー\(C\)とソレノイド\(L\)のみをつないだ回路はどうだろうか。 \[V_C=V_L\] \[\frac{Q}{C}=-L\frac{dI}{dt}\] 時間で微分し、\(-L\)で割ると、 \[\frac{d^2I}{dt^2}=-\frac{1}{LC}I\tag{1}\] これは単振動の方程式ではないか！ \[I(t)=C_1\cos(\frac{1}{\sqrt{LC}}t+C_2)\] 両辺に\(dI\)を掛けて、(1)式を変形してみよう。まず左辺から、 \[\frac{d^2I}{dt^2}dI=\frac{d\dot I}{dt}\frac{dI}{dt}dt=\frac{d}{dt}\left(\frac{1}{2}\dot I^2\right)dt\] 次は右辺 \[-\frac{1}{LC}IdI\] 両辺を\((I(t_0), I(t))\)の範囲で積分しよう。 \[\int_{t_0}^{t}d\left(\frac{1}{2}\dot I^2(t)\right)=\int_{I(t_0)}^{I(t)}-\frac{1}{LC}IdI\] \[\frac{1}{2}\dot I^2(t)-\frac{1}{2}\dot I^2(t_0)=\frac{1}{2\sqrt{LC}}I^2(t_0)-\frac{1}{2\sqrt{LC}}I^2(t)\] \(I(t_0)=I_0,\ \dot I(t_0)=\dot I_0\)とすれば \[\frac{1}{2}\dot I^2+\frac{1}{2\sqrt{LC}}I^2=\frac{1}{2}\dot I_0^2+\frac{1}{2\sqrt{LC}}I_0^2\] こ...これはエネルギー保存則！このように物理の中の分野が違っていても同じような構造があるのがとても面白い。