楽しい科学（理論）チャンネル

今回はマクスウェル方程式について まずは電磁気学の基本方程式となるべく選ばれた方程式たち４選!

1.ガウスの法則(電気)

　立体領域\(V\)内の総電荷\(Q_V\)は、境界\(\partial V\)での電束密度\(\boldsymbol{D}\)の面積分に等しい。 \[\iint_{\partial V}\boldsymbol{D}(\boldsymbol{r},t)\cdot d\boldsymbol{S}=Q_V\tag{1}\]

2.ガウスの法則(磁気)

　立体領域\(V\)の境界\(\partial V\)での磁束密度\(\boldsymbol{B}\)の面積分は0になる。 \[\iint_{\partial V}\boldsymbol{B}(\boldsymbol{r},t)\cdot d\boldsymbol{S}=0\tag{2}\]

3.アンペールの法則

　平面領域\(S\)を貫く電流\(I\)は、境界\(\partial S\)での磁場\(\boldsymbol{H}\)の面積分に等しい。 \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=I\tag{3}\]

4.ファラデーの法則

　平面領域\(S\)を貫く磁束密度\(\boldsymbol{B}\)の面積分の時間変化は、境界\(\partial S\)での電場\(\boldsymbol{E}\)の線積分に等しい。 \[\int_{\partial S}\boldsymbol{E}(\boldsymbol{r},t)\cdot d\boldsymbol{r}=-\frac{\partial}{\partial t}\iint_{S}\boldsymbol{B}(\boldsymbol{r},t)\cdot d\boldsymbol{S}\tag{4}\]

まずこれらの方程式を同じ１点で扱うために各方程式が１点で成り立つ形に直したい。電荷密度\(\rho(\boldsymbol{r},t)\)が\(\iiint_{V}\rho(\boldsymbol{r},t)dV:=Q_V\)を満たすものとして、 \[\iint_{\partial V}\boldsymbol{D}(\boldsymbol{r},t)\cdot d\boldsymbol{S}=\iiint_{V}\rho(\boldsymbol{r},t)dV\] ガウスの定理を用いると、 \[\iiint_{V}\nabla\cdot\boldsymbol{D}(\boldsymbol{r},t)dV=\iiint_{V}\rho(\boldsymbol{r},t)dV\] 領域\(V\)を点とみなせるくらい小さくすると、 \[\nabla\cdot\boldsymbol{D}(\boldsymbol{r},t)=\rho(\boldsymbol{r},t)\tag{5}\] 磁束密度も同様に \[\nabla\cdot\boldsymbol{B}(\boldsymbol{r},t)=0\tag{6}\] (5),(6)式をガウス・マクスウェルの法則と呼ぶことにしよう。 立体領域の電荷の時間変化(領域は時間変化しないとして)について考えてみよう。電荷が突然現れたり、消えたりしないため、立体領域内の電荷が時間的に変化している場合は、境界から電荷出入りしていると考えられる。領域内の電荷を\(Q_V(\boldsymbol{r},t)\)境界から出入りする電流の和を\(I_{\partial V}(\boldsymbol{r},t)\)とすると、

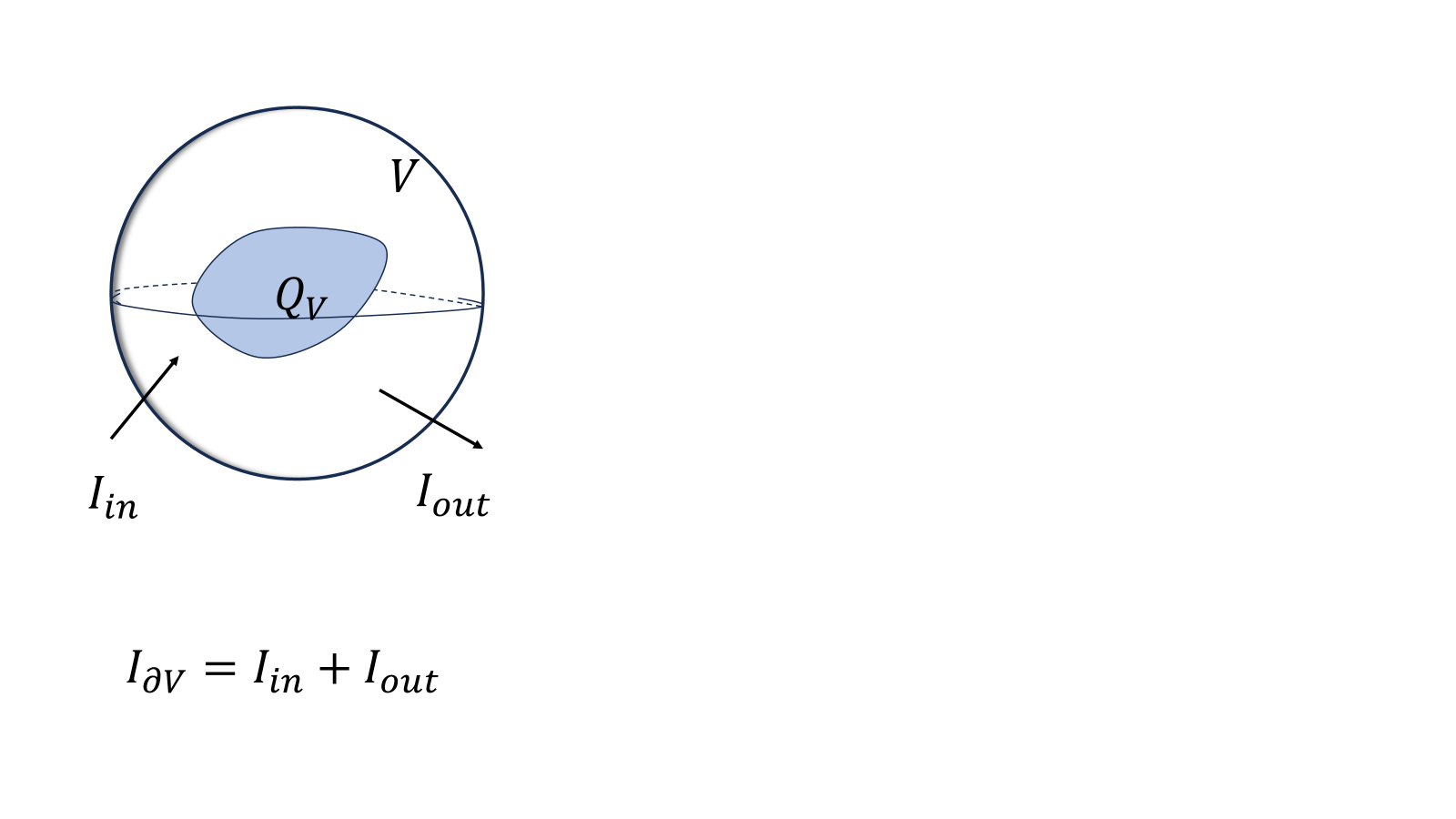
\[\frac{\partial}{\partial t}Q_V(\boldsymbol{r},t)=I_{\partial V}(\boldsymbol{r},t)\] \[\frac{\partial}{\partial t}\iiint_V\rho(\boldsymbol{r},t)=\iint_{\partial V}-\boldsymbol{j}(\boldsymbol{r},t)\cdot d\boldsymbol{S}\] (電荷の増減の符号と、\(I_{\partial V}\)の符号を一致させたとき面積要素ベクトルとの内積の符号が逆になるのでマイナスを付けた。例えば電荷が増えたら\(jdS\gt0\)とするため)右辺にガウスの定理を使うと、 \[\frac{\partial}{\partial t}\iiint_V\rho(\boldsymbol{r},t)=-\iiint_{V}\nabla\cdot\boldsymbol{j}(\boldsymbol{r},t)dV\] \[\frac{\partial}{\partial t}\rho(\boldsymbol{r},t)=-\nabla\cdot\boldsymbol{j}(\boldsymbol{r},t)\] この方程式を電荷保存則という。電荷が時間的に大きくなっている場合は領域に入ってくる電流が大きく、逆に電荷が時間的に小さくなっている場合、領域から出ていく電流が大きいということを方程式にしたものだ。ガウス・マクスウェルの法則を使うと、 \[\frac{\partial}{\partial t}\nabla\cdot\boldsymbol{D}(\boldsymbol{r},t)=-\nabla\cdot\boldsymbol{j}(\boldsymbol{r},t)\tag{6}\] マクスウェルはこの法則もマクスウェル方程式に内包したいと考えている。3番目の式をストークスの定理を利用して \[\int_{\partial S}\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=I\] \[\iint_{S}\nabla\times\boldsymbol{H}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S}\boldsymbol{j}(\boldsymbol{r})\cdot d\boldsymbol{r}\] 曲面領域\(S\)が点とみなせるほど小さくすると、 \[\nabla\times\boldsymbol{H}(\boldsymbol{r})=\boldsymbol{j}(\boldsymbol{r})\] と表すことができる。しかしこの式の発散(右から\(\nabla\cdot\))を取ると、 \[\nabla\cdot(\nabla\times\boldsymbol{H})=\frac{\partial}{\partial x}\left(\frac{\partial H_z}{\partial y}-\frac{\partial H_y}{\partial z}\right)\] \[+\frac{\partial}{\partial y}\left(\frac{\partial H_x}{\partial z}-\frac{\partial H_z}{\partial x}\right)+\frac{\partial}{\partial z}\left(\frac{\partial H_y}{\partial x}-\frac{\partial H_x}{\partial y}\right)\] \[\nabla\cdot(\nabla\times\boldsymbol{H})=0\] つまり、 \[\nabla\cdot\boldsymbol{j}=0\] となる。時間的に電流が変化する場合は、(6)式を満たさなければならないと考えたマクスウェルは \[\nabla\times\boldsymbol{H}(\boldsymbol{r},t)=\boldsymbol{j}(\boldsymbol{r},t)+\frac{\partial}{\partial t}\boldsymbol{D}(\boldsymbol{r},t)\] と電束密度の時間変化の項を入れてアンペールの法則を補正した。これをアンペール・マクスウェルの法則と呼ぶことにしよう。ファラデーの法則もストークスの定理を使って、 \[\int_{\partial S}\boldsymbol{E}(\boldsymbol{r},t)\cdot d\boldsymbol{r}=-\frac{\partial}{\partial t}\iint_{S}\boldsymbol{B}(\boldsymbol{r},t)\cdot d\boldsymbol{S}\] \[\iint_{S}\nabla\times\boldsymbol{E}(\boldsymbol{r},t)\cdot d\boldsymbol{r}=-\frac{\partial}{\partial t}\iint_{S}\boldsymbol{B}(\boldsymbol{r},t)\cdot d\boldsymbol{S}\] \[\nabla\times\boldsymbol{E}(\boldsymbol{r},t)=-\frac{\partial}{\partial t}\boldsymbol{B}(\boldsymbol{r},t)\] こちらをファラデー・マクスウェルの法則と呼ぶことにしよう。

＊＊マクスウェルの方程式＊＊

　1.ガウス・マクスウェルの法則(電気) \[\nabla\cdot\boldsymbol{D}(\boldsymbol{r},t)=\rho(\boldsymbol{r},t)\] 　2.ガウス・マクスウェルの法則(磁気) \[\nabla\cdot\boldsymbol{B}(\boldsymbol{r},t)=0\] 　3.アンペールマクスウェルの法則 \[\nabla\times\boldsymbol{H}(\boldsymbol{r},t)=\boldsymbol{j}(\boldsymbol{r},t)+\frac{\partial}{\partial t}\boldsymbol{D}(\boldsymbol{r},t)\] 　4.ファラデー・マクスウェルの法則 \[\nabla\times\boldsymbol{E}(\boldsymbol{r},t)=-\frac{\partial}{\partial t}\boldsymbol{B}(\boldsymbol{r},t)\]

　超有名な方程式ですね。なんでこんなに有名になったかというと、電磁気の現象の説明がこの式で付くのもそうなのだが、電磁波の予言が大きい。この式がどのようにして電磁波の存在の示唆になったのか見ていこう。

/*　補足　波動方程式

　波(波動)を表す簡単な例として、 \[f(x,t)=A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\] のような関数がある。\(A\)を振幅(波の高さ)、\(T\)を周期、\(\lambda\)を波長という。この波の時間\(t\)の偏微分を見てみよう。 \[\frac{\partial}{\partial t}f(x,t)=\frac{2\pi}{T}A\cos2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\] もう一回偏微分すればもとの関数の形に戻りそうだ。 \[\frac{\partial^2}{\partial t^2}f(x,t)=-\frac{4\pi^2}{T^2}A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)=\frac{4\pi^2}{T^2}f(x,t)\tag{7}\] 位置\(x\)の偏微分も計算しよう。 \[\frac{\partial^2}{\partial x^2}f(x,t)=-\frac{4\pi^2}{\lambda^2}A\sin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)=-\frac{4\pi^2}{\lambda^2}f(x,t)\tag{8}\] (7)、(8)式から \(f(x,t)=\frac{T^2}{4\pi^2}\frac{\partial^2}{\partial t^2}f(x,t),\ f(x,t)=\frac{\lambda^2}{4\pi^2}\frac{\partial^2}{\partial t^2}f(x,t)\)この２つの性質を１つの式で表してみよう。この２つの式を引くと \[\left(\frac{\lambda^2}{4\pi^2}\frac{\partial^2}{\partial x^2}-\frac{T^2}{4\pi^2}\frac{\partial^2}{\partial t^2}\right)f(x,t)=0\] 両辺を\(\frac{\lambda^2}{4\pi^2}\)で割る。波の速さは\(v=\lambda/T\) \[\left(\frac{\partial^2}{\partial x^2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2}\right)f(x,t)=0\] この式を1次元の波動方程式という。

終わり*/

真空中では\(\boldsymbol{B}=\mu_0\boldsymbol{H},\ \boldsymbol{D}=\epsilon_0\boldsymbol{E}\)なのでマクスウェル方程式を\(\boldsymbol{B},\boldsymbol{E}\)の式で表してみよう。 \[\nabla\cdot\boldsymbol{E}(\boldsymbol{r},t)=\frac{1}{\epsilon_0}\rho(\boldsymbol{r},t)\] \[\nabla\cdot\boldsymbol{B}(\boldsymbol{r},t)=0\] \[\nabla\times\boldsymbol{B}(\boldsymbol{r},t)=\mu_0\boldsymbol{j}(\boldsymbol{r},t)+\mu_0\epsilon_0\frac{\partial}{\partial t}\boldsymbol{E}(\boldsymbol{r},t)\] \[\nabla\times\boldsymbol{E}(\boldsymbol{r},t)=-\frac{\partial}{\partial t}\boldsymbol{B}(\boldsymbol{r},t)\] 電荷や電流がないような点について考えると、電荷密度\(\rho=0,\ \boldsymbol{j}=\boldsymbol{0}\) \[\nabla\cdot\boldsymbol{E}(\boldsymbol{r},t)=0\tag{9}\] \[\nabla\cdot\boldsymbol{B}(\boldsymbol{r},t)=0\tag{10}\] \[\nabla\times\boldsymbol{B}(\boldsymbol{r},t)=\mu_0\epsilon_0\frac{\partial}{\partial t}\boldsymbol{E}(\boldsymbol{r},t)\tag{11}\] \[\nabla\times\boldsymbol{E}(\boldsymbol{r},t)=-\frac{\partial}{\partial t}\boldsymbol{B}(\boldsymbol{r},t)\tag{12}\] (11)の時間微分は \[\nabla\times\frac{\partial}{\partial t}\boldsymbol{B}(\boldsymbol{r},t)=\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\boldsymbol{E}(\boldsymbol{r},t)\] (12)がで代入できる。 \[\nabla\times(\nabla\times\boldsymbol{E}(\boldsymbol{r},t))=-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\boldsymbol{E}(\boldsymbol{r},t)\] 右辺の\(z\)成分を計算してみる。(めんどくさそう。なので外積は苦手である。) \[[\nabla\times(\nabla\times\boldsymbol{E})]_z\] \[=\frac{\partial }{\partial x}[\nabla\times\boldsymbol{E}]_y-\frac{\partial }{\partial y}[\nabla\times\boldsymbol{E}]_x\] \[=\frac{\partial}{\partial x}\left(\frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}\right)-\frac{\partial}{\partial y}\left(\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}\right)\] \[=\frac{\partial}{\partial z}\left(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}\right)-\frac{\partial^2 E_z}{\partial x^2}-\frac{\partial^2 E_z}{\partial y^2}\] \[=\frac{\partial}{\partial z}\left(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\right)-\frac{\partial^2 E_z}{\partial x^2}-\frac{\partial^2 E_z}{\partial y^2}-\frac{\partial^2 E_z}{\partial z^2}\] \[=[\nabla(\nabla\cdot\boldsymbol{E})]_z-[\nabla^2\cdot\boldsymbol{E}]_z\] 他の成分も同様なので、 \[\nabla\times(\nabla\times\boldsymbol{E})=\nabla(\nabla\cdot\boldsymbol{E})-\nabla^2\cdot\boldsymbol{E}\] これと(9)式から \[\nabla\times 0-\nabla^2\cdot\boldsymbol{E}(\boldsymbol{r},t)=-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\boldsymbol{E}(\boldsymbol{r},t)\] \[\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\right)\boldsymbol{E}(\boldsymbol{r},t)=\boldsymbol{0}\] (12)を時間微分して、(11)を代入すれば \[\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}-\mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\right)\boldsymbol{B}(\boldsymbol{r},t)=\boldsymbol{0}\] 電場、磁場(磁束密度)は３次元で広がる波であったのだ。マクスウェルが電磁波を発表した時の透磁率、誘電率は分からないが、真空中の透磁率\(\mu_0\)、誘電率\(\epsilon_0\)をそれぞれ \[\mu_0=1.2566\times10^{-6}\ \mathrm{kg\ m\ s^{-2}\ A^{-2}}\] \[\epsilon_0=8.8554\times10^{-12}\ \mathrm{kg^{-1}\ m^{-3}\ s^{4}\ A^{2}}\] としよう。 \[\frac{1}{\sqrt{\mu_0\epsilon_0}}\simeq 2.998\times10^{8}\ \mathrm{m\ s^{-1}}\] 光速度\(c\)は、 \[c:=299\ 792\ 458\ \mathrm{m\ s^{-1}}\] で定義されるのでほぼ同じ値を取る。そのため電場、磁場は光速度の波となる。電場と地場の波を電磁波とよび、光の速さで空間全方向に進む。