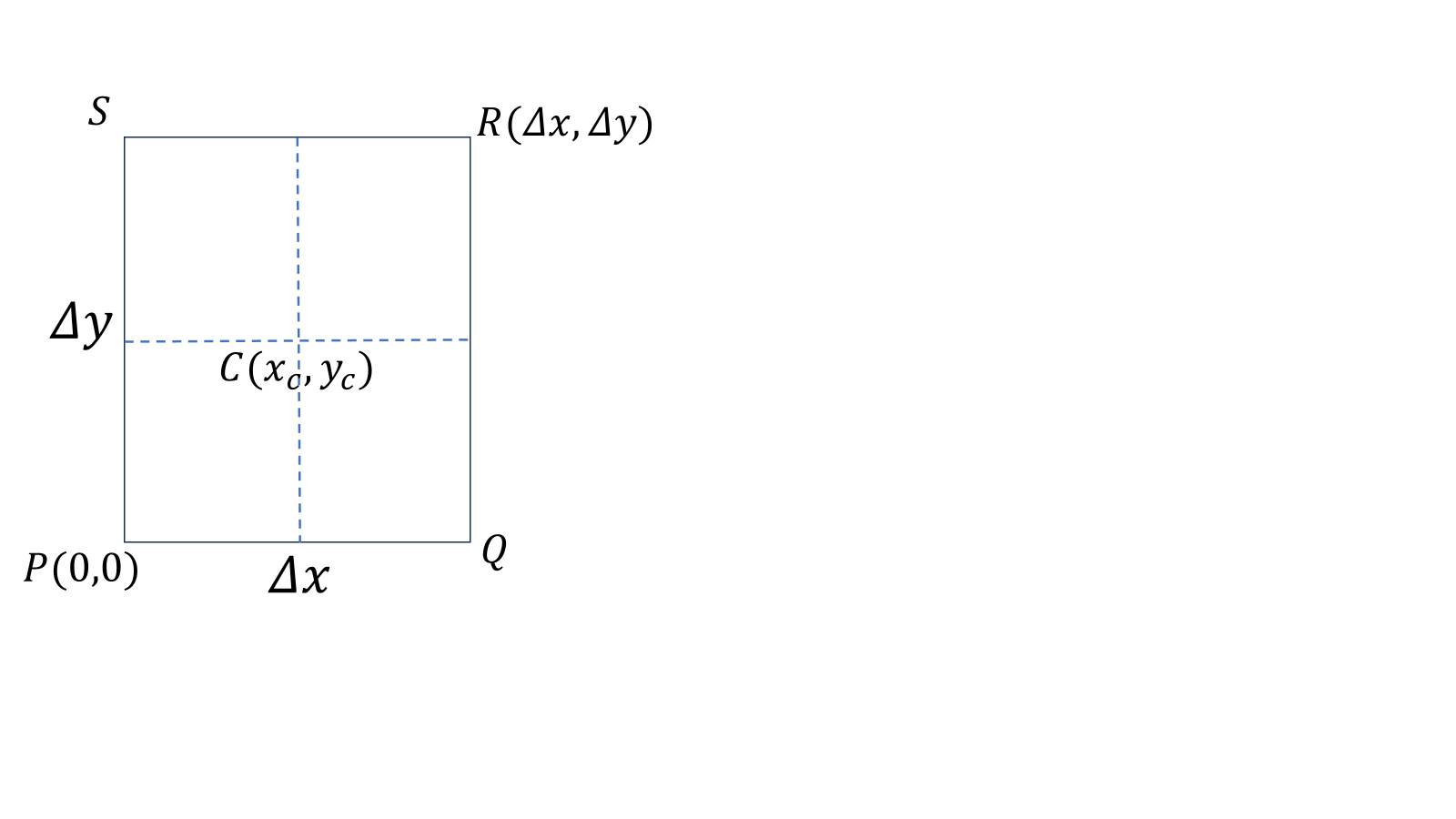楽しい科学（理論）チャンネル

　

ベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)の面積分を説明したい。\(xy\)平面上の領域\(S\)面積分を \[\iint_Sf(x,y)dxdy=\sum_{i=0}^{\infty}\sum_{j=0}^{\infty}f(x_i,y_j)\varDelta x_i\varDelta y_j\] のように計算することができる。あまり目に見える例が思い浮かばない、、平面\(S\)に加わる力\(F\)を\(F=\iint_S p(x,y)dxdy\)のように圧力\(p\)が\(x,y\)によるで関数になっている場合も計算することができる。しかし平坦な面とは限らないため曲面での積分が必要になる。点とみなせるくらい小さい面\(\varDelta S\)その点である関数が\(f(x,y,z)\)と表せる場合、3次元空間上の曲面\(S\)の積分を \[\iint_Sf(x,y,z)dS:=\sum_{i=0}^{\infty}f(x_i,y_i,z_i)\varDelta S_i\] と定める。この定義と下でやっているベクトルを使った定義の面積分も同値であることを示せるはずだが僕には難しいどうしても外積の概念がないと説明できない。外積を使わないでもできるはずなのだが、、、

3次元空間に曲面\(S\)とベクトル場\(\boldsymbol{A}\)があったとしよう。曲面\(S\)の法線単位ベクトル\(\boldsymbol{n}\)とする。を\(N\)個の分割にしてそのうち１つを\(\varDelta S_i\)とする。\(\varDelta S_i\)が十分に小さいとすれば、\(\varDelta S_i\)の曲がりがないものとみなしてその面の法線単位ベクトル\(\boldsymbol{n}_i\)が定まる。分割を無限に小さくしていくことで、面積分を \[\iint_S\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{S}:=\sum_i^{\infty}\boldsymbol{A}(\boldsymbol{r_i})\cdot \boldsymbol{n}_i\varDelta S_i\] のように計算することにする。成分で表すと、 \[\iint_S\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{S}\] \[=\iint_S(A_x(x,y,z)dydz+A_y(x,y,z)dzdx+A_z(x,y,z)dxdy)\] この計算も一般に簡単にはできない。計算の工夫を少しながら書いていく。

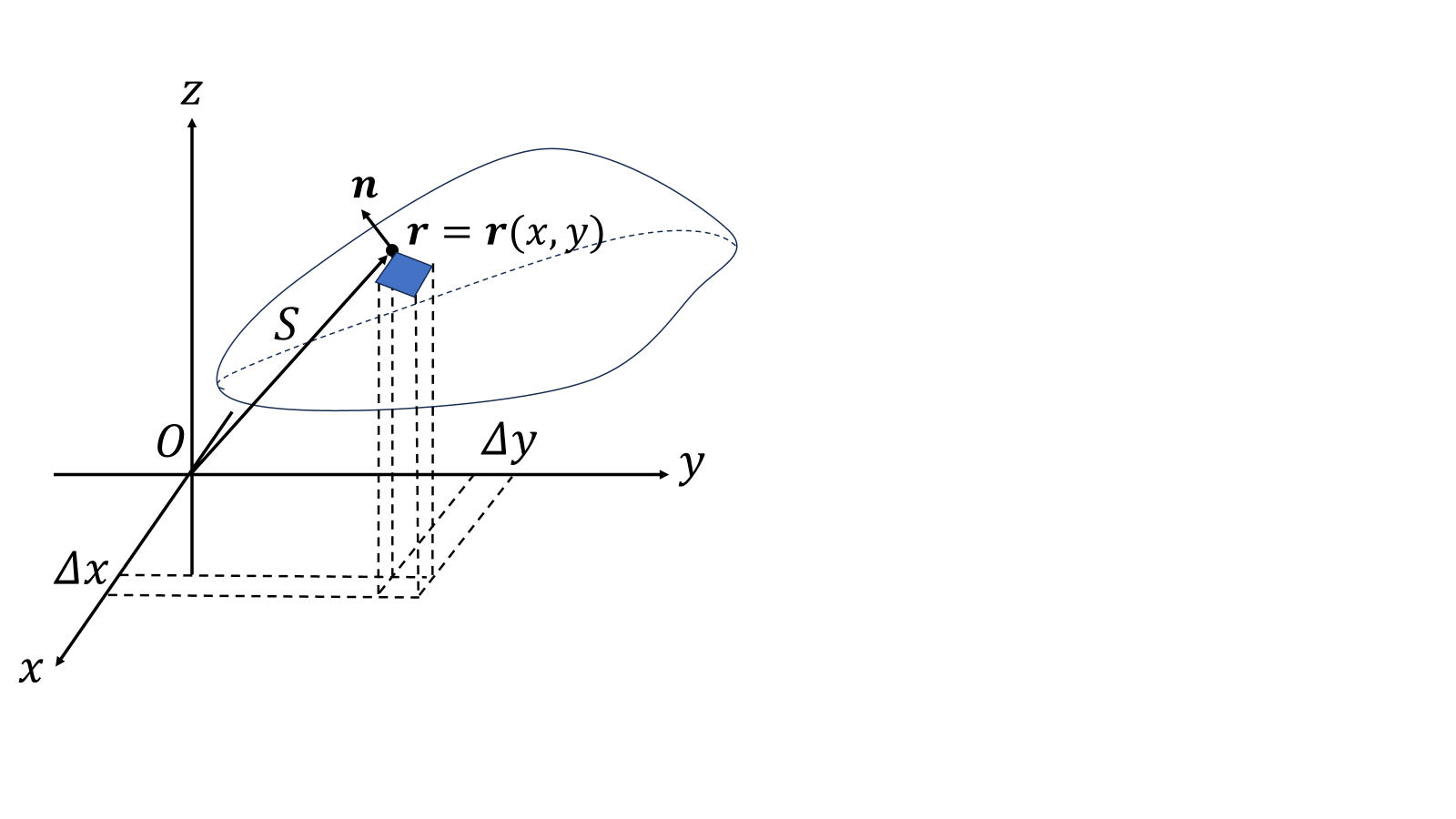
曲面上の点が\(\boldsymbol{r}=\boldsymbol{r}(x\ y\ f(x,y))\)のようにベクトル関数で与えられている場合、\(\varDelta S\)は \[\varDelta\boldsymbol{r}_x=\boldsymbol{r}(x+\varDelta x,y)-\boldsymbol{r}(x,y)\] \[\varDelta\boldsymbol{r}_y=\boldsymbol{r}(x,y+\varDelta y)-\boldsymbol{r}(x,y)\] として平行四辺形の面積とみて \[\varDelta S\simeq|\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y|\] と表せる。法線単位ベクトルは \[\boldsymbol{n}\simeq\frac{\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y}{|\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y|}\] \[\boldsymbol{n}\varDelta S=\frac{\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y}{|\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y|}|\varDelta\boldsymbol{r}_x\times\varDelta\boldsymbol{r}_y|\] \[\boldsymbol{n}\varDelta S=\left(\frac{\varDelta\boldsymbol{r}_x}{\varDelta x}\times\frac{\varDelta\boldsymbol{r}_y}{\varDelta y}\right)\varDelta x\varDelta y\] である。\(\varDelta x,\varDelta y\to0\)の極限を取ると、 \[d\boldsymbol{S}=\left(\frac{\partial \boldsymbol{r}}{\partial x}\times\frac{\partial \boldsymbol{r}}{\partial y}\right)dxdy\] この式の外積部分とベクトル場\(\boldsymbol{A}(x,y,z(x,y))\)との内積を計算することで、\(\iint_Df(x,y)dxdy\)のような積分の計算に持ち込むと計算が楽な場合がある。 自分で好きに曲面を取れる場合は、常にベクトル場と法線ベクトルの間の角が同じ角度になるようにすることもかなり有効だ。 これから示すストークスの定理をコンパクトに記述するためにベクトル場の回転\(\nabla\times\)について説明する。まずは\(\nabla\)は \[\nabla:=\frac{\partial}{\partial x}\boldsymbol{e}_x+\frac{\partial}{\partial y}\boldsymbol{e}_y+\frac{\partial}{\partial z}\boldsymbol{e}_z\] である。単位ベクトルで外積を取ってから偏微分するので、\(\nabla\times\boldsymbol{A}\)は \[\nabla\times\boldsymbol{A}=\begin{pmatrix}\frac{\partial}{\partial x}\\\frac{\partial}{\partial y}\\\frac{\partial}{\partial z}\end{pmatrix}\times\begin{pmatrix}A_x\\A_y\\A_z\end{pmatrix}=\begin{pmatrix}\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\\\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}\\\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\end{pmatrix}\] である。

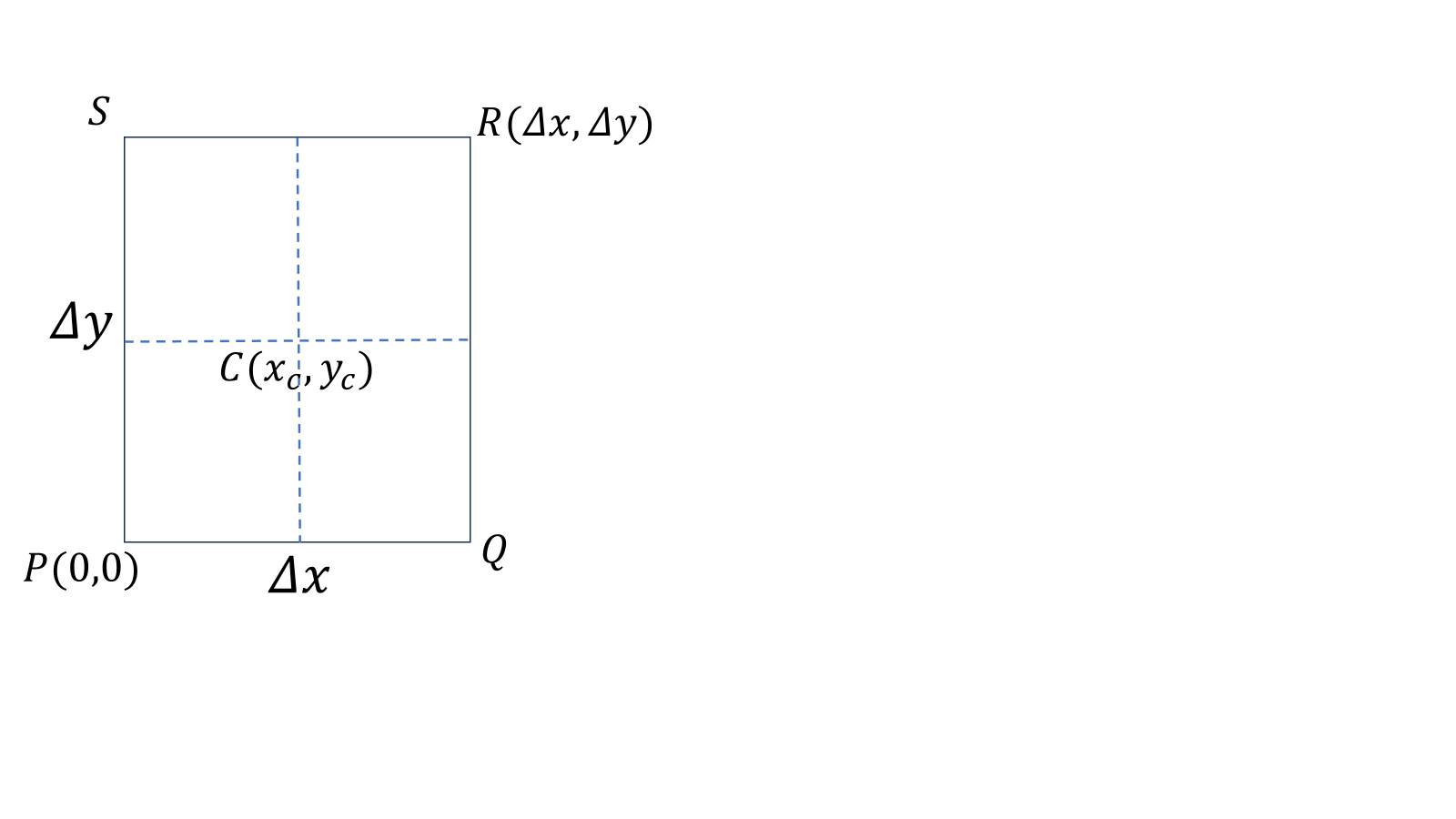
ストークスの定理は線積分を面積分に変える定理なのだが、任意の曲面について成り立つことを証明するのは難しい。そこで、面積\(s_z=\varDelta x\varDelta y\)の小さい長方形\(PQRS\)について、ストークスの定理を証明しよう。長方形の境界\(\partial s_z\)の線積分が、長方形の面積分と等しいことを示すことを目標にする。始めに線積分の結果を\((x_c,y_c)=(\varDelta x/2,\varDelta y/2)\)でテイラー展開する。\(\varDelta x,\varDelta y\)の２次以上の項を\(0\)とみなす。 \[\int_{PQ}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=A_x(x_c,0)\varDelta x\] \[=A_x(x_c,y_c-\frac{\varDelta y}{2})\varDelta x\simeq A_x(x_c,y_c)\varDelta x-\frac{1}{2}\frac{\partial A_x}{\partial y}\varDelta x\varDelta y\] \[\int_{QR}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=A_y(\varDelta x,y_c)\varDelta y\] \[=A_y(x_c+\frac{\varDelta x}{2},y_c)\varDelta y\simeq A_y(x_c,y_c)\varDelta y+\frac{1}{2}\frac{\partial A_y}{\partial x}\varDelta x\varDelta y\] \[\int_{RS}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=A_x(x_c,\varDelta y)(-\varDelta x)\] \[=-A_x(x_c,y_c+\frac{\varDelta y}{2})\varDelta x\simeq -A_x(x_c,y_c)\varDelta x-\frac{1}{2}\frac{\partial A_x}{\partial y}\varDelta x\varDelta y\] \[\int_{SP}\boldsymbol{A}(\boldsymbol{r}) \cdot d\boldsymbol{r}=A_y(0,y_c)(-\varDelta y)\] \[=-A_y(x_c-\frac{\varDelta x}{2},y_c)\varDelta y\simeq A_y(x_c,y_c)\varDelta y+\frac{1}{2}\frac{\partial A_y}{\partial x}\varDelta x\varDelta y\] 全て足すと、 \[\int_{\partial s_z}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\left(\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\right)\varDelta x\varDelta y\] \[\int_{\partial s_z}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\int_{s_z}\nabla\times\boldsymbol{A}(\boldsymbol{r})\cdot \boldsymbol{e}_zdxdy\] \(s_x=\varDelta y\varDelta z,s_y=\varDelta z\varDelta x\)についても同じ積分が成り立つ。 任意の曲面\(S\)が\(s_x,s_y,s_z\)の集まりで表せたとすると、

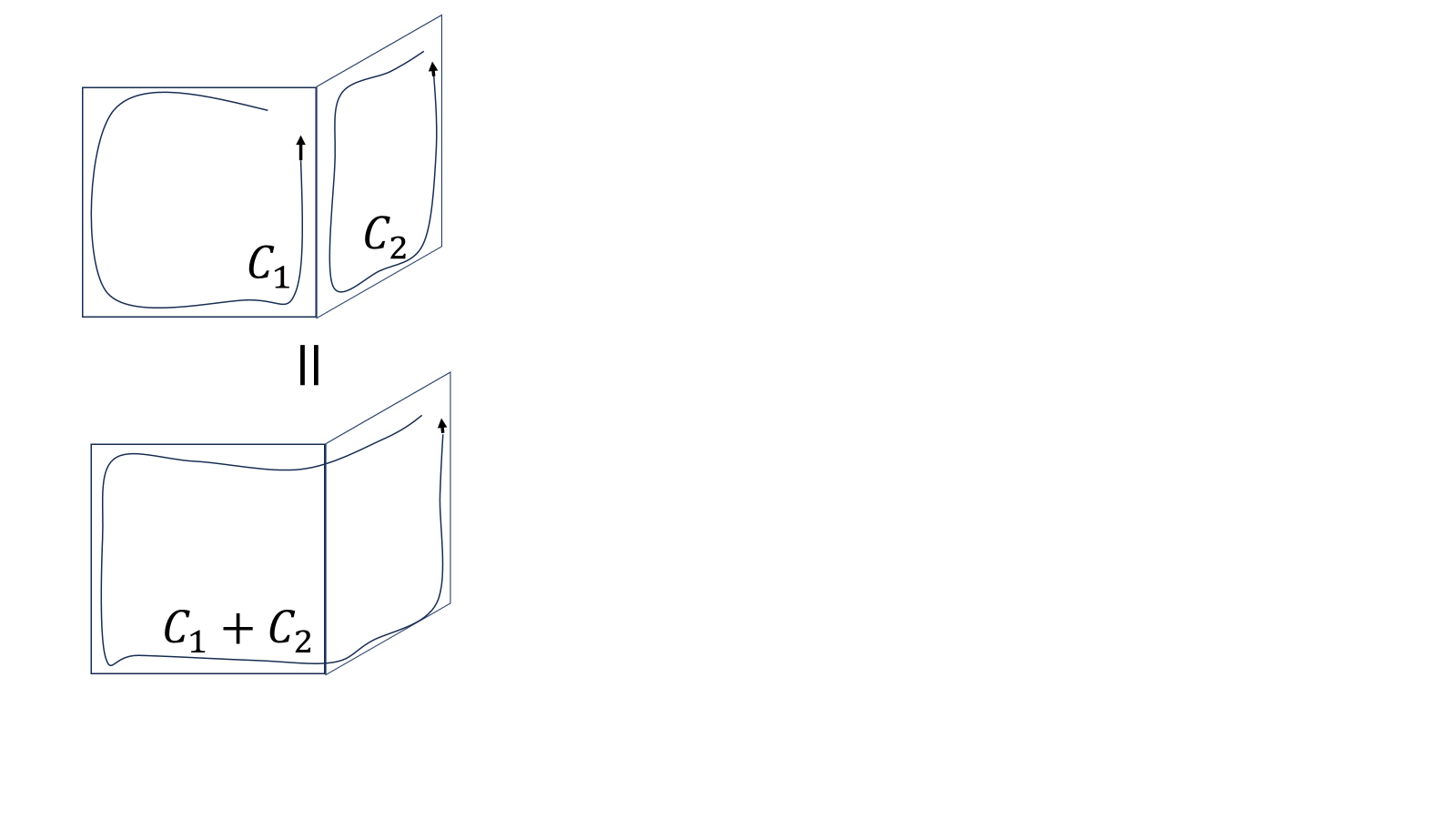
隣り合う経路同士は逆向きの経路積分になり打ち消すため\(\partial S\)のみが残るため、 \[\int_{\partial S}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S}\nabla\times\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{S}\] が成り立つ。直観的で正しい証明ではないが、分かりやすいと思う。

＊＊ストークスの定理＊＊

ベクトル場\(\boldsymbol{A}\)と任意の曲面\(S\)について \[\int_{\partial S}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{r}=\iint_{S}\nabla\times\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{S}\]