楽しい科学(理論)チャンネル
ガウスの定理
今回はガウスの定理を説明する。体積分を面積分に変える定理であり、物理でもよく使う。ベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)と任意(表面は曲面になるような)の3次元領域\(V\)があったとしよう。
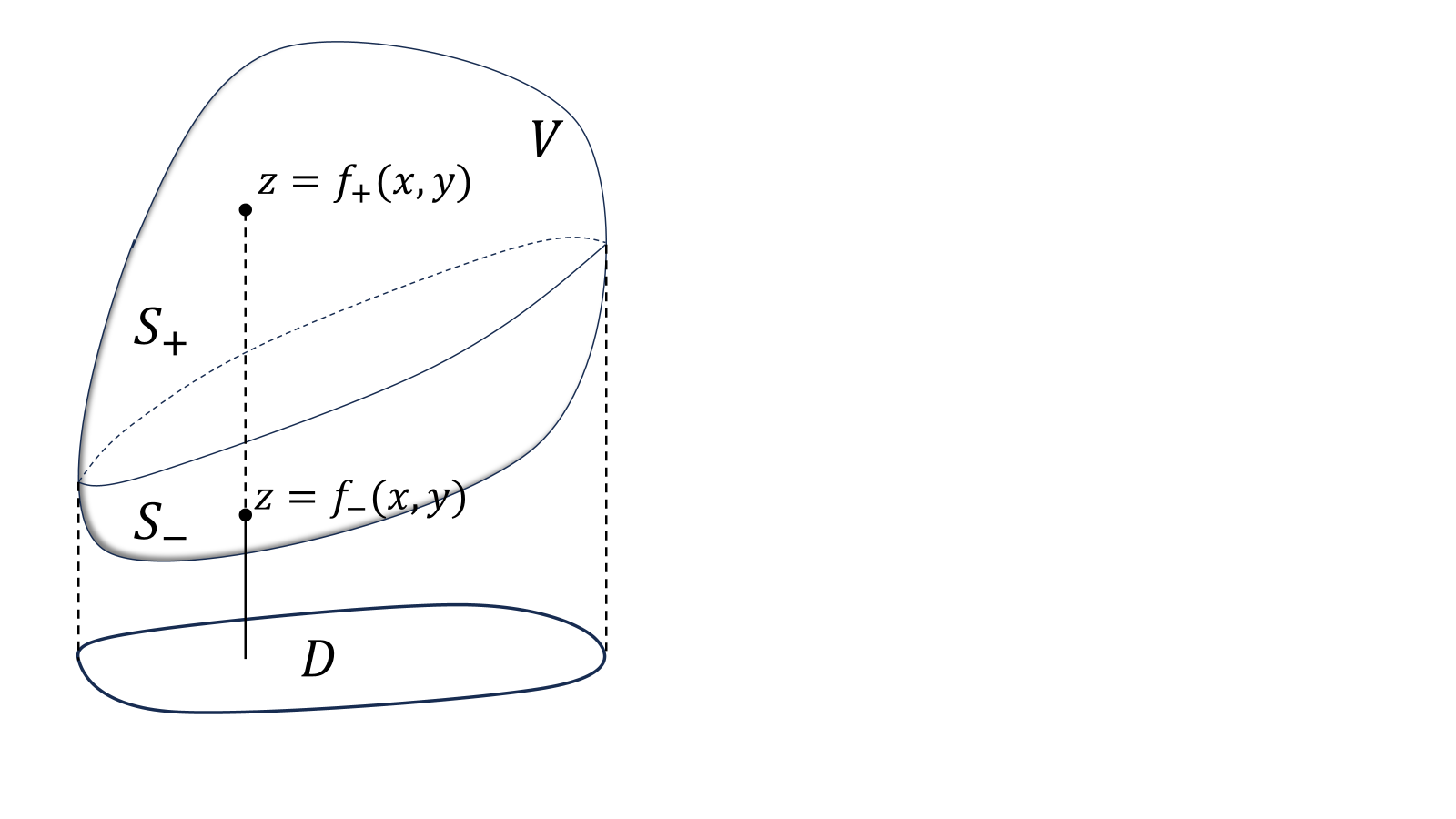
領域\(V\)の\(xy\)平面への射影を\(D\in ℝ^2\)とする。関数\(f_+,\ f_-\)は\(f_+:D\to S_+,\ f_-:D\to S_-\)となるものとする。
\[I_z=\iiint_V \frac{\partial A_z(x,y,z)}{\partial z}dxdydz\]
の積分を計算してみよう。
\[I_z=\iint_{D}\int_{z=f_-}^{z=f_+}\frac{\partial A_z(x,y,z)}{\partial z}dz dxdy\]
\[=\iint_{D}A_z(x,y,f_+(x,y))dxdy-\iint_{D}A_z(x,y,f_-(x,y))dxdy\]
\(z\)軸方向の単位ベクトルを\(\boldsymbol{n}_z\)とすると\(S_+\)では\(\boldsymbol{A}\cdot\boldsymbol{n}_z=A_z\)、\(S_-\)では\(\boldsymbol{A}\cdot\boldsymbol{n}_z=-A_z\)なので、
\[I_z=\iint_{S_+}\boldsymbol{A}\cdot\boldsymbol{n}_zdxdy+\iint_{S_-}\boldsymbol{A}\cdot\boldsymbol{n}_zdxdy\]
\[=\iint_{\partial V}\boldsymbol{A}\cdot\boldsymbol{n}_zdxdy\]
同様にして\(I_x,I_y\)を計算して、\(I_x+I_y+I_z\)を計算する。
\[I_x+I_y+I_z=\iiint_V \left(\frac{\partial A_x
}{\partial x}+\frac{\partial A_z
}{\partial y}+\frac{\partial A_y
}{\partial z}\right)dxdydz\]
\[=\iiint_V \nabla\cdot\boldsymbol{A}dxdydz\]
面積分として計算した\(I_x+I_y+I_z\)は
\[I_x+I_y+I_z=\iint_{\partial V}(\boldsymbol{A}\cdot\boldsymbol{n}_xdydz+\boldsymbol{A}\cdot\boldsymbol{n}_ydzdx+\boldsymbol{A}\cdot\boldsymbol{n}_zdxdy)\]
\[=\iint_{\partial V}(A_xdydz+A_ydzdx+A_zdxdy)=\iint_{\partial V}\boldsymbol{A}\cdot d\boldsymbol{S}\]
**ガウスの定理**
ベクトル場\(\boldsymbol{A}\)と任意の立体領域\(V\)について
\[\iint_{\partial V}\boldsymbol{A}(\boldsymbol{r})\cdot d\boldsymbol{S}=\iiint_{V}\nabla\cdot\boldsymbol{A}(\boldsymbol{r}) dV\]
せっかくなのでガウスの定理を使ってみよう。
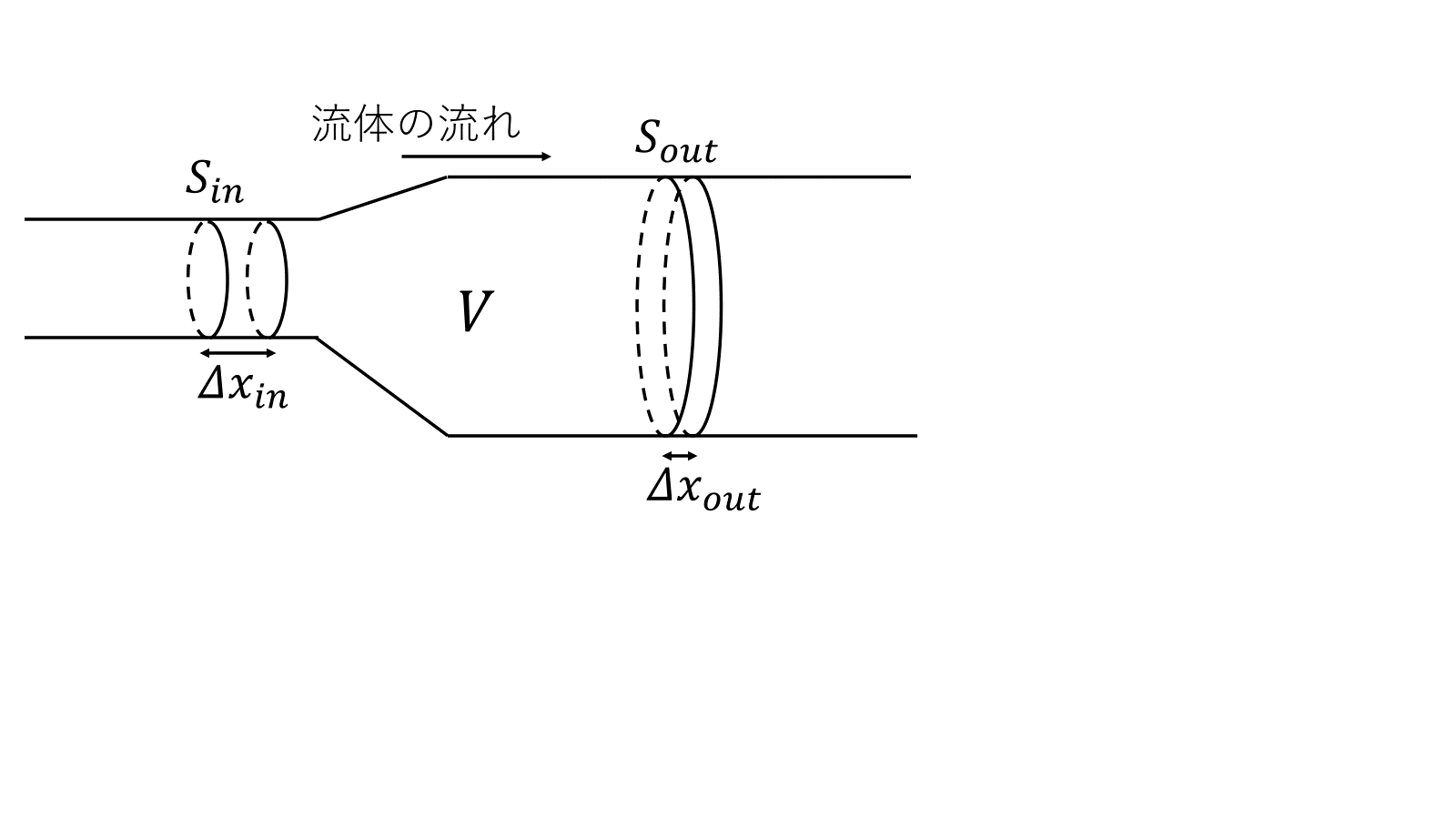
今回の例で使う圧縮流体は、空気のように圧縮可能な流体のことである。水などは圧力をかけても体積が変わらないため非圧縮流体という。粘性を考えると難しいのでさらさらの流体でいこう!図のようなパイプがある。ここに圧縮流体が右から左に流れているとしよう。図のように領域を\(V\)を取ろう。パイプの側面を\(S_{side}=\partial V-S_{in}-S_{out}\)、領域\(V\)の流体の質量を\(m_V\)、密度を\(\rho(x)\)、\(\varDelta t\)の間に\(S_{in}\)にあった流体は\(\varDelta x_{in}\)、\(S_{out}\)にあった流体は\(\varDelta x_{out}\)まで動き、\(\varDelta t\)の間に\(V\)の質量は\(\varDelta m_V\)増えたとすると、
\[\varDelta m_V=\rho(x_{in})S_{in}\varDelta x_{in}-\rho(x_{out})S_{out}\varDelta x_{out}\tag{1}\]
\(x_{in}\in S_{in},\ x_{out}\in S_{out}\)である。この式は流体の質量の増加\(\varDelta m_V\)は入ってきた流体の質量と出ていった流体の質量の差であるということを式にしたものである。\(\varDelta t\)で両辺を割り、\(\varDelta t\to0\)の極限を取る。
\[\frac{\partial}{\partial t}m_V=\rho(x_{in})v(x_{in})S_{in}-\rho(x_{out})v(x_{out})S_{out}\]
\(S_{out}\)の面積要素ベクトルを\(\boldsymbol{e}_x\)とすると、\(S_{in}\)の面積要素ベクトルは\(-\boldsymbol{e}_x\)となる。つまり、\(d\boldsymbol{S}_{in}=-\boldsymbol{e}_xdS_{in},\ d\boldsymbol{S}_{out}=\boldsymbol{e}_xdS_{out}\)となる。
\[\frac{\partial}{\partial t}m_V=-\iint_{S_{in}}\rho(x)\boldsymbol{v}(x)\cdot d\boldsymbol{S}-\iint_{S_{out}}\rho(x)\boldsymbol{v}(x)\cdot d\boldsymbol{S}\]
\(S_{side}\)と流体の速度ベクトル\(\boldsymbol{v}\)は常に平行なので、\(-\iint_{S_{side}}\rho \boldsymbol{v}\cdot d\boldsymbol{S}=0\)右辺に足して、\(\partial V=S_{in}+S_{side}+S_{out}\)なので1つの積分にまとめる。
\[\frac{\partial}{\partial t}m_V=-\iint_{\partial V}\rho(x)\boldsymbol{v}(x)\cdot d\boldsymbol{S}\]
ここでガウスの定理を使う。
\[\frac{\partial}{\partial t}m_V=-\iiint_{V}\nabla\cdot(\rho(x)\boldsymbol{v}(x))dV\]
左辺も\(\rho(x)\)を使った式で表すと、
\[\frac{\partial}{\partial t}\iiint_V\rho(x)dV=-\iiint_{V}\nabla\cdot(\rho(x)\boldsymbol{v}(x))dV\]
\(V\)を点とみなせるくらい小さくとるを
\[\frac{\partial}{\partial t}\rho(x)=-\nabla\cdot(\rho(x)\boldsymbol{v}(x))\]
今回は\(x\)成分しか考えなかったが、これを流体力学で連続の方程式という。式自体はかなりコンパクトでかつ点でも使える式なので汎用性が高い。しかし、抽象的で分かりにくい。本質は(1)式である。任意の領域の質量が増減している場合は、領域の境界から入ってくる流量と出ていく流量に差があるというわけである。
次の例は磁気の基本方程式の1つガウスの法則である。
\[\nabla\cdot\boldsymbol{B}(\boldsymbol{x})=0\]
空間の任意の点\(\boldsymbol{x}\)で磁束密度\(\boldsymbol{B}\)の発散は0になるというものだ。任意の領域\(V\)で体積分する。
\[\iiint_V\nabla\cdot\boldsymbol{B}(\boldsymbol{x})dV=0\]
ガウスの定理を使うと
\[\iint_{\partial V}\boldsymbol{B}(\boldsymbol{x})\cdot d\boldsymbol{S}=0\]
任意の領域に入ってくる磁束流と領域から出ていく磁束流が等しいことをこの式は表している。
/* 余談
昔何かの本で読んだことかもしれないが、筆者は電磁気の電場、が流体の圧縮流体(粘性や渦無し)にかなり対応が似ていると感じる。電荷量保存則
\[\frac{\partial}{\partial t}\rho=-\nabla\cdot\boldsymbol{j}\]
というものがある。任意の点で電流密度の発散の変化は電荷密度の時間変化に等しいという法則がある。
圧縮流体は、連続の方程式
\[\frac{\partial}{\partial t}\rho=-\nabla\cdot(\rho\boldsymbol{v})\]
がある。電磁気には電流密度\(\boldsymbol{j}\)というものがあり、領域の境界の法線方向のベクトル\(\frac{dm}{dt}=\iint_{\partial V}\boldsymbol{j}_m\cdot d\boldsymbol{S}\)となる\(\boldsymbol{j}_m\)を定義すると、
電荷量保存則と全く同じ形で書くことができる。
\[\frac{\partial}{\partial t}\rho=-\nabla\cdot\boldsymbol{j}_m\]
終わり*/

