一般相対性理論のページをもっと分かり易く作れると思ったので、こちらで新しく作り直します。一般相対性理論は等価原理、一般相対性原理、アインシュタイン方程式の３つを基盤に作られた理論です。一旦局所的という考え方を捨ててかつ1次元で相対論のイメージを紹介します。

　等価原理は重力加速度\(g\)による重力\(F_g\)と、系の加速度\(\alpha\)による慣性力\(F_I\)の区別がつかないことをいいます。慣性力のイメージがわかないと思いますが、車の中でアクセルを踏んで加速度運動しているとき別に何かに押されているわけでもないのに加速している方向と逆向きに働いているように感じる力です。この原理の本質は重力加速度\(g\)の空間にいても加速度\(\alpha=g\)で運動をする系にいれば、重力を感じないことにあります。系にいる人に働く力\(F\)は \[F=F_g+F_I=mg-m\alpha=0\] となります。つまり力を感じないということですね。\(\alpha=g\)の加速度運動と言いましたが要は、自由落下です。自由落下している系の中では重力を感じないということです。

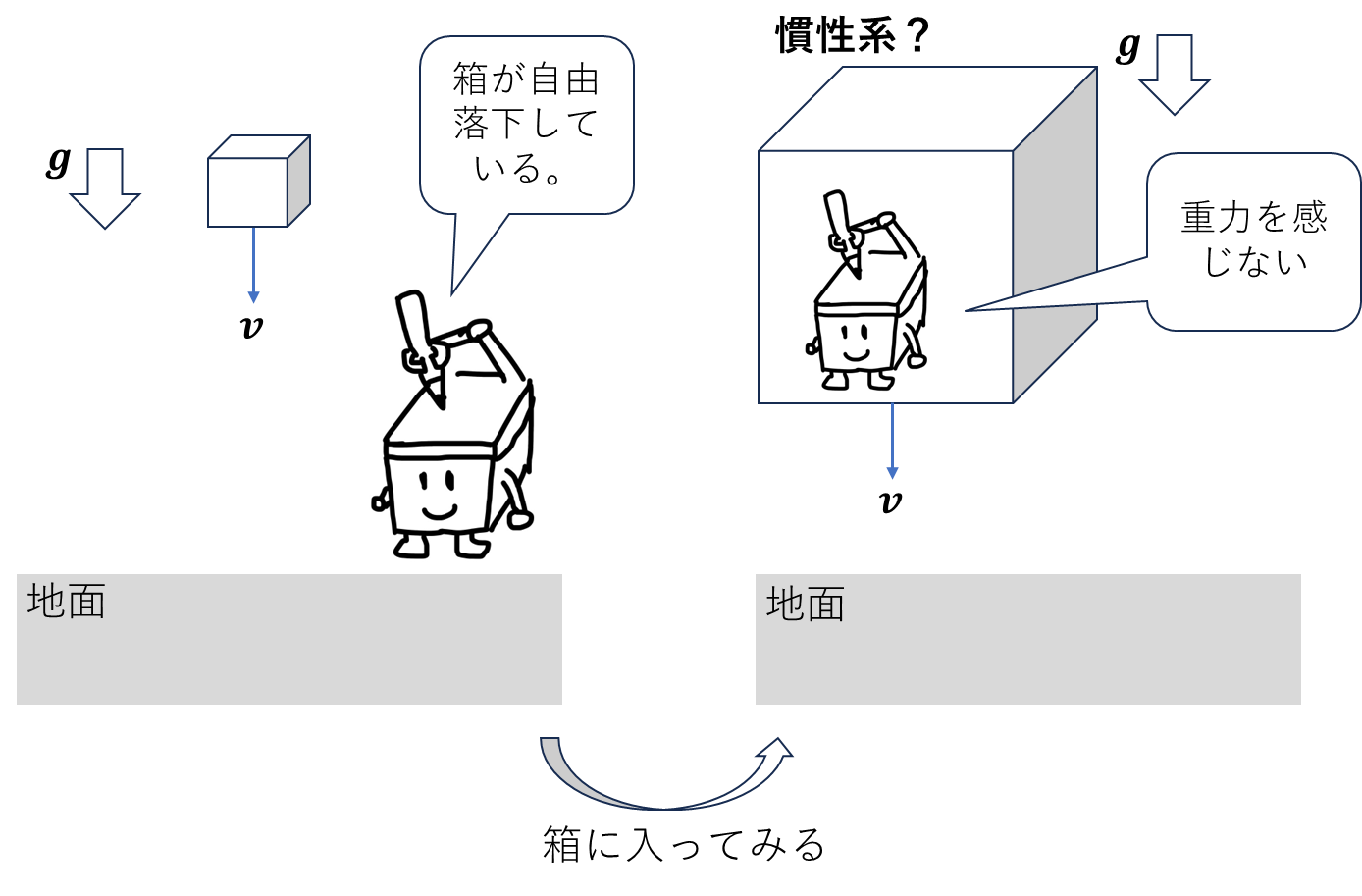
　一様な重力場で箱が自由落下している状況を想像してください。地面にいる人から見ると、箱は加速度運動をして見えます。しかし箱にいると箱が受ける慣性力と重力のつり合いから箱の中では何も力が働いていないように感じます。このような加速度系だけど、重力の影響を無視できる系を局所慣性系と呼びます。ではこの箱を宇宙に２つだけ用意したらどうなるでしょうか。

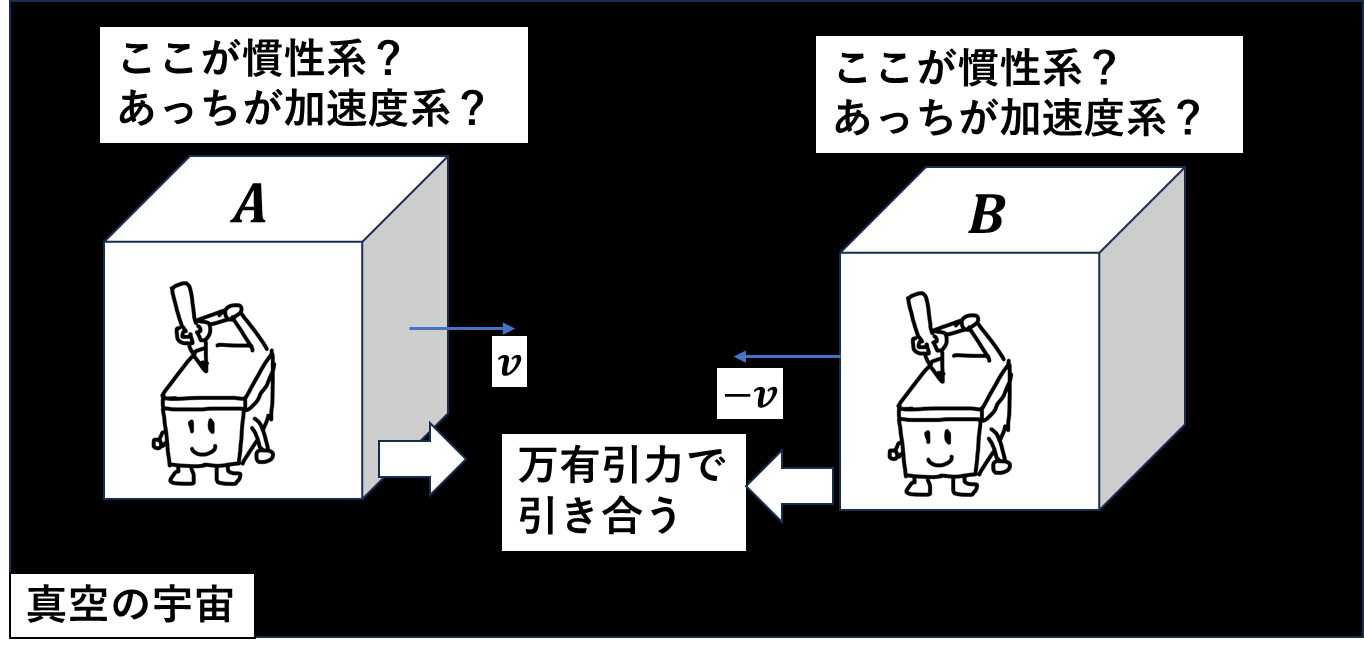
　さっきの例では地面が慣性系で箱が加速度系であることが明確でしたが、この例はどうでしょう。\(A\)が慣性系であれば\(B\)が自由落下してきているように見えます。\(B\)が慣性系ならば\(A\)が自由落下しているように見えます。(古典力学的には両方加速度系でそれぞれが近づいていると考えます。)等価原理は、重力による加速度系と慣性系の等価性(区別が付かないこと)も表します。

　一般相対性原理は任意の加速度系(等価な座標系)で同じ物理法則が使えるという要請です。局所慣性系と慣性系は等価な座標だから同じ物理法則が使えるべきだと考えた訳ですね。今からの話は厳密な話ではありません。イメージをもってもらうための説明になります。局所慣性系と慣性系の２人からで自由落下する箱の運動を考えます。ここでは速さを\(u\)時間を\(\tau\)と表すことにします。

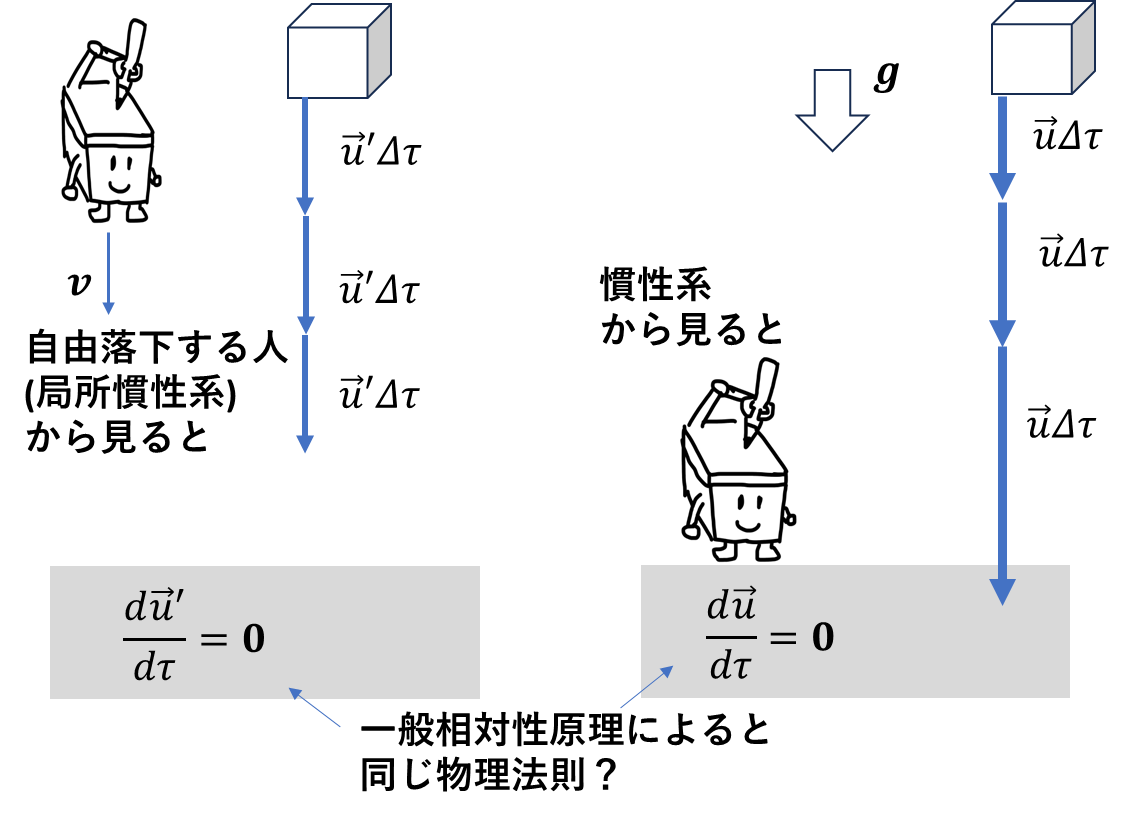
　局所慣性系から見た箱は静止もしくは等速直線運動をして見えます。質量で割った箱の運動方程式は \[\frac{d\vec{u}'}{d\tau}=\boldsymbol{0}\] となります。一般相対性原理によると慣性系からみた箱の運動方程式も \[\frac{d\vec{u}}{d\tau}=\boldsymbol{0}\] とならなくてはなりません。古典力学的には箱の中では、\(\vec{\alpha}=\boldsymbol{0}\)、地面に立っている人から見ると、\(\vec{\alpha}=-\vec{g}\)となるで矛盾しているように感じますね。これを解決したのが重力は軸の目盛りを変えるという発想です。

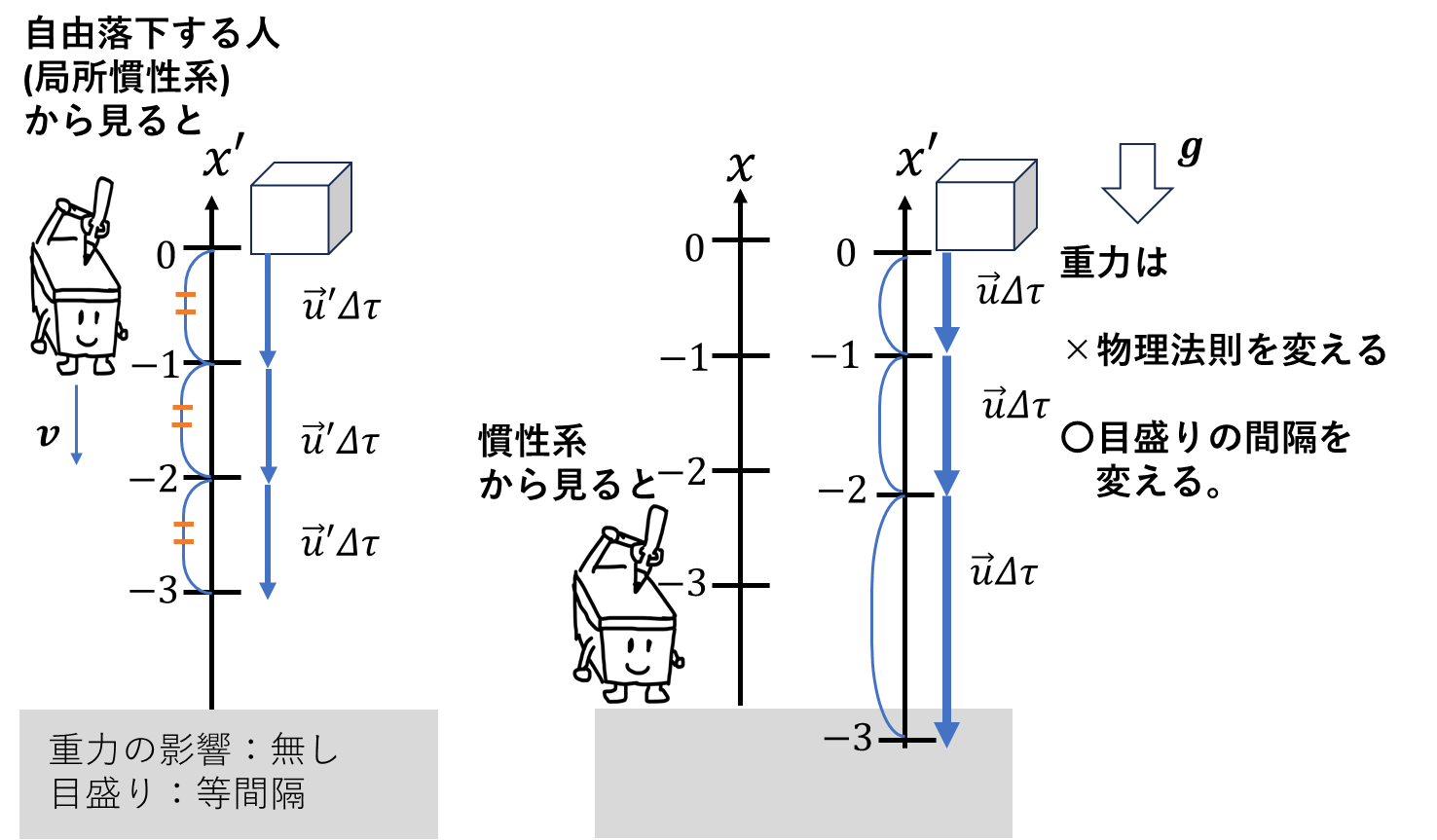
　局所慣性系の目盛りは慣性系の座標から見ると重力の影響で目盛りの間隔が変化します。１マスを決める基底ベクトルも変化しています。これを慣性系の目盛りで測ると加速度運動に見える訳です。速度ベクトル\(\vec{u}\)速さ\(u\)と基底ベクトル\(\boldsymbol{e}\)の積で表すことにします。局所慣性系では、基底ベクトルはただの定ベクトルなので、 \[\frac{d\vec{u}}{d\tau}=\frac{du}{d\tau}\boldsymbol{e}_x=\boldsymbol{0}\] \[\frac{du}{d\tau}=0\] となります。速度変化が０という結果が得られます。慣性系から見ると、基底ベクトルは位置によって変化するので、 \[\frac{d\vec{u}}{d\tau}=\frac{du}{d\tau}\boldsymbol{e}+u\frac{d\boldsymbol{e}}{d\tau}=\boldsymbol{0}\] 合成関数の微分が必用になります。ベクトルは成分×基底ベクトルと表したいので、クリストッフェルの記号\(\Gamma\)を \[\Gamma\boldsymbol{e}=\frac{d\boldsymbol{e}}{dx}\] と定義します。これにより、 \[\frac{du}{d\tau}\boldsymbol{e}=-u\frac{d\boldsymbol{e}}{d\tau}=-u\frac{dx}{d\tau}\frac{d\boldsymbol{e}}{dx}\] \[\frac{du}{d\tau}\boldsymbol{e}=-\Gamma u^2\boldsymbol{e}\] \[\frac{du}{d\tau}=-\Gamma u^2\] となります。ちゃんと加速度運動になりましたね。ただ\(\Gamma u^2\)はなんなんだと思うかもしれません。アインシュタイン方程式から、計量テンソル\(g_{11}\)というものが求まります。実は\(\Gamma\)は計量テンソルから求めることができます。それにより、\(u^2\Gamma=g\)と分かるのです。相対性理論は空間と時間の４次元で作られた理論で今の話は正しいわけではないです。ただ等価原理、一般相対性原理のイメージがつかめたかと思います。また相対性理論のどの辺りを勉強しているのか目安にもなるかと思います。

\[G_{\mu\nu}+\Lambda g_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\] この方程式は時空間のマス目の間隔、正確には計量テンソルを決める方程式です。後で詳しく述べます。

　難易度★☆☆☆☆　１.一般相対性理論の概要

　難易度★☆☆☆☆　２.ローレンツ変換

　難易度★★☆☆☆　３.計量テンソル

　難易度★★☆☆☆　４.固有時

　難易度★★☆☆☆　５.測地線方程式

　難易度★★★☆☆　６.クリストッフェルの記号

　難易度★★★★☆　７.アインシュタイン方程式

　難易度★★★☆☆　８.アインシュタイン方程式を解く準備

　難易度★★★☆☆　９.アインシュタイン方程式を万有引力に帰着させる。

　難易度★★★★★　１０.シュワルツシルト解

　難易度★★★★☆　１１.シュワルツシルト時空での惑星の軌跡

　難易度★★★★☆　１２.一般相対性理論での光

たった１２ステップで一般相対性理論の基礎的な内容を理解できるように作りました。