楽しい科学（理論）チャンネル

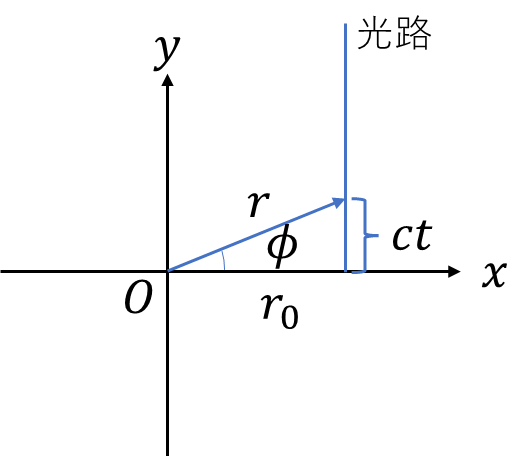
　始めに初期条件を付けて、保存量を決めます。\(t=0\)で光が\(y\)軸正に、\((r,\phi)=(r_0,0)\)を通過したことにします。\(t=0\)付近で、 \[\phi\simeq\sin\phi=\frac{ct}{r_0},\ \frac{d\phi}{dt}=\frac{c}{r_0}\] と近似できます。\(t=0\)で \[r^2\frac{d\phi}{dt}=r_0^2\frac{c}{r_0}=r_0c\] この保存則を使うことで、動径\(r\)の１階時間微分、２階時間微分から\(t\)を消去できます。 \[\frac{dr}{dt}=-r^2\frac{d}{dt}\frac{1}{r}=-r^2\frac{d\phi}{dt}\frac{d}{d\phi}\frac{1}{r}\] \[\frac{dr}{dt}=-r_0c\frac{d}{d\phi}\frac{1}{r}\] \(r\)の２階時間微分は、 \[\frac{d^2r}{dt^2}=\frac{d}{dt}\frac{dr}{dt}=\frac{d\phi}{dt}\frac{d}{d\phi}\frac{dr}{dt}=\frac{r_0c}{r^2}\frac{d}{d\phi}\frac{dr}{dt}\] \[\frac{d^2r}{dt^2}=-\frac{r_0^2c^2}{r^2}\frac{d^2}{d\phi^2}\frac{1}{r}\tag{1}\] これは後で使います。局所慣性系\((\bar{x^\mu})\)での固有時を考えてみます。局所慣性系で光速度\(c\)は、 \[c=\sqrt{\left(\frac{d\bar x}{d\bar t}\right)^2+\left(\frac{d\bar y}{d\bar t}\right)^2+\left(\frac{d\bar z}{d\bar t}\right)^2}\] と表せます。これを固有時の定義に代入します。 \[-c^2d\tau^2=-(cd\bar{t})^2+(d\bar{x})^2+(d\bar{y})^2+(d\bar{z})^2\] \[=-\left[c^2-\left(\frac{d\bar x}{d\bar t}\right)^2+\left(\frac{d\bar y}{d\bar t}\right)^2+\left(\frac{d\bar z}{d\bar t}\right)^2\right]d\bar t^2=0\] \[=-(c^2-c^2)d\bar t^2=0\] この簡単な計算から、固有時の変化量は０になります。このことから重力場での光路を求めます。 \[-\left(1-\frac{r_s}{r}\right)c^2dt^2+\frac{dr^2}{1-r_s/r}+r^2d\phi^2=0\] これが一般座標に座標変換した光の固有時の式です。両辺を\(dt^2\)で割ります。 \[-\left(1-\frac{r_s}{r}\right)c^2+\frac{1}{1-r_s/r}\left(\frac{dr}{dt}\right)^2+r^2\left(\frac{d\phi}{dt}\right)^2=0\] 両辺に\((1-r_s/r)\)を掛けます。保存則も使います。 \[-\left(1-\frac{r_s}{r}\right)^2c^2+\left(\frac{dr}{dt}\right)^2+\frac{r_0^2c^2}{r^2}\left(1-\frac{r_s}{r}\right)=0\] 両辺を時間で微分して、\(dr/dt\)で両辺を割ります。 \[2\frac{r_s}{r^2}\left(1-\frac{r_s}{r}\right)c^2+2\frac{d^2r}{dt^2}-\frac{2r_0^2c^2}{r^3}+\frac{3r_0^2c^2r_s}{r^4}=0\] \[\frac{d^2r}{dt^2}=-\frac{r_sc^2}{r^2}+\frac{r_s^2c^2+r_0^2c^2}{r^3}-\frac{3r_0^2c^2r_s}{2r^4}\] (1)式を代入します。 \[-\frac{r_0^2c^2}{r^2}\frac{d^2}{d\phi^2}\frac{1}{r}=-\frac{r_sc^2}{r^2}+\frac{r_s^2c^2+r_0^2c^2}{r^3}-\frac{3r_0^2c^2r_s}{2r^4}\] シュワルツシルト半径\(r_s\)は\(r_0\)よりとても小さい数字なので、\(r_s^2/r_0^2\simeq 0\)とします。 \[\frac{d^2}{d\phi^2}\frac{1}{r}=\frac{r_s}{r_0^2}-\frac{1}{r}+\frac{3r_s}{2r^2}\] \[\frac{d^2}{d\phi^2}\frac{1}{r}=\frac{2GM}{c^2r_0^2}-\frac{1}{r}+\frac{3GM}{c^2r^2}\] これがシュワルツシルト時空での光路の式になっていると私は思います。こちらの式は文献などを参考にしていないので間違ってたらすいません。

　シュワルツシルト時空のある固定された2点\(A,B\)があるとします。空間成分は変化せず、\(dr=d\theta=d\phi=0\)時間だけ過ぎている状況を考えます。 \[-(c\varDelta \bar{t})^2=-(c\varDelta \tau)^2=-\left(1-\frac{r_s}{r}\right)(c\varDelta t)^2\] 点\(A,B\)の時間の遅れを求めていきます。ここでは一般座標での時間経過\(\varDelta t\)に対して\(A,B\)の局所慣性系での時間\(\varDelta \bar t\)がどれほど遅れているか求めてみます。なぜそのようにしなければいけないかと言うと、\(A,B\)はともに自分の座標系が慣性系であると思い込んで時間を測っているからだと私は解釈しています。 \[\varDelta \bar t_A=\sqrt{1-\frac{r_s}{r_A}}\ \varDelta t,\ \varDelta \bar t_B=\sqrt{1-\frac{r_s}{r_B}}\ \varDelta t\] これらの式から\(\varDelta t\)を消去すると、 \[\varDelta \bar t_A=\sqrt{\frac{1-r_s/r_A}{1-r_s/r_B}}\varDelta \bar t_B\] これがシュワルツシルト時空での２点の時間の遅れを表す式です。このままでは分かりずらいので、 \[r_A=\frac{4}{3}r_s,\ r_B=\infty\] とします。\(A\)は特異点に近くて、\(B\)は重力の影響がないくらい遠いということですね。 \[\varDelta \bar t_A=\sqrt{\frac{1-3/4}{1-0}}\varDelta \bar t_B=\frac{1}{2}\varDelta \bar t_B\] 特異点から十分に遠い\(B\)での１秒は点\(A\)での0.5秒になります。強い重力場の方が時間がゆっくり流れます。一般にシュワルツシルト時空では \[\varDelta t_A\lt\varDelta t_B\ (r_A\lt r_B)\] が成り立ちます。光は波でありその波の周期\(T\)を使うことで波長\(\lambda\)は、 \[\lambda=cT\] と表すことができます。強い重力場では時間が送れます。光の周期も遅れると考えると、 \[T_A\lt T_B\ (r_A\lt r_B)\] となります。両辺に光速度を掛けることで、 \[\lambda_A\lt \lambda_B\] 波長\(\lambda\)も重力によって変わってしまいます。強い重力場で出た光の波長が引き延ばされるので光は赤っぽい方にシフトして見えます。

楽しい科学（理論）チャンネル

シュワルツシルト時空での光路

赤方偏移