このページでは特殊相対性理論をざっくり説明していきます。特殊相対性理論の基本原理は２つで、光速度不変の原理、特殊相対性原理です。光速度不変の原理は、真空中の光速度はどの慣性系から見ても同じ速さであるという原理で、特殊相対性原理はどの慣性系でも同じ物理法則が成り立つという原理です。光速度不変は直観は古典力学に反しています。光速度は系に依らず\(c\)なので相対速度も\(c\)です。これを実現するため相対性理論では時空間の長さが系によって一致しません。系によって時間、位置を別の記号で表します。

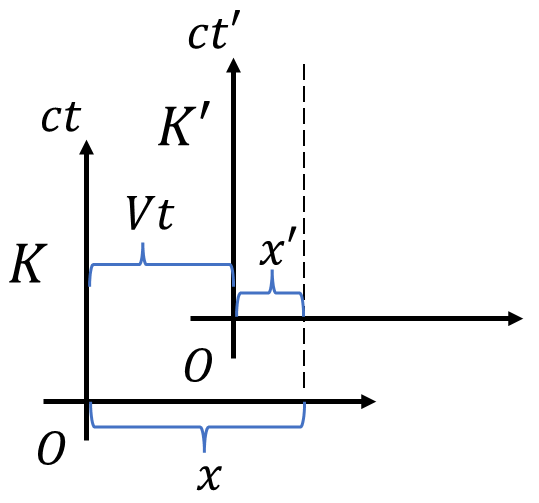
　特殊相対性理論では、時間×光速度\(c\)と空間の4次元空間\((ct,x,y,z)\)を使います。この直交座標系をミンコフスキー空間といいます。簡単にするため空間を\(x\)の1次元とします。　慣性系(静止もしくは等速直線運動している、乗り物みたいなのを想像してもらっていいです。)\(K(ct,x)\)\(K'(ct',x')\)があり、\(t=t'=0\)で原点が一致していて、\(K'\)は一定の速度\(V\)で\(K\)から離れていく場面を考えます。古典力学的には時間の進みが系に依らないので、 \[t'=t\] また図から\(K\)でのある位置\(x\)は\(K'\)で \[x'=x-Vt\tag{1}\] と表せますね。これを\((ct,x)\to(ct,x')\)の座標変換とみなしてガリレイ変換といいます。一旦この考えは捨ててください。

(1)式に\(x=ct\)を代入すると、つまり\(t=0\)で光を放ちその到達点を\(x\)とするということですね。 \[x'=(c-V)t\] \(K'\)では光の速さが\(c-V\)となってしまい、光速度不変の原理に反します。そこで光速度不変の新たにローレンツ変換を導出します。 \[\begin{cases}ct'=A(ct)+Bx\\ x'=C(ct)+Dx\end{cases}\tag{2}\] 速度\(V\)に依る\(A,B,C,D\)は定数です。なぜ1次変換(2乗以上を含まない)変換なのかというと、逆変換も同じ形になってほしいからです。2次以降があると逆変換にルートなどが入ってしまうからです。\(K\)から見て\(x'=0\)の位置は\(x=Vt\)となります。これを(2)式に代入します。 \[\begin{cases}ct'=A(ct)+BVt\\ 0=C(ct)+DVt\end{cases}\] 下の式を使うと、 \[C=-\frac{V}{c}D\] これを(2)式に戻すと \[\begin{cases}ct'=A(ct)+Bx\\ x'=D(-Vt+x)\end{cases}\tag{3}\] となります。(3)式は\(K\)からx軸正の方向に一定の速度\(V\)で移動する系の座標系を求める変換です。\(L:(ct,x)\mapsto(ct',x')\)と書くことにしましょう。

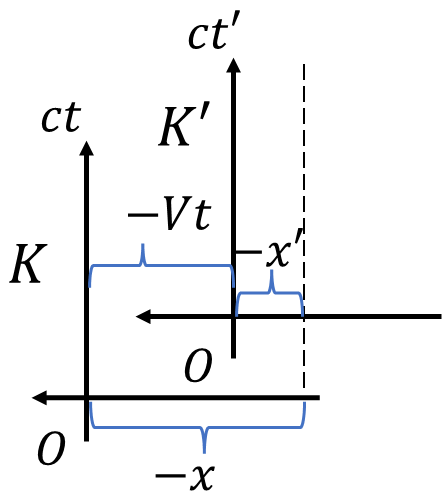
　\(x\)軸を逆向きにしてみるとどうでしょうか。\(K'\)から見て、\(K\)は\(x\)軸正の方向に一定の速度\(V\)で移動する系に見えるでしょう。つまり先ほどと同じ変換\(L\)が使えて、\(L:(-ct',-x')\mapsto(-ct,-x)\)となるはずです。これを(4)式とします。軸が逆向きなので、\(x,x'\)の符号が逆になる点に注意して、 \[-x=D(-Vt'-x')\tag{4},\ x'=-Vt'+\frac{x}{D}\] (3)式の下段と、(4)式から\(x'\)を消去すると、 \[-Vt'+\frac{x}{D}=D(-Vt+x),\ -Vt'=-DVt+\frac{D^2-1}{D}x\] \[t'=Dt-\frac{D^2-1}{DV}x\] 気づいたでしょうか、定数\(A,B\)が定数\(D\)を使って表すことができています。 \[\begin{cases}ct'=D(ct)+\frac{(D^2-1)c}{DV}x\\ x'=D(-Vt+x)\end{cases}\tag{3}\] 光速度不変の原理より、\(t=t'=0\)で発した光の位置はそれぞれの座標で、\(x=ct,x'=ct'\)になるので、(5)式に代入します。まずは(4)式から、 \[ct'=-Vt'+\frac{ct}{D},\ t'=\frac{ct}{D(c+V)}\] (5)式は、 \[t'=Dt-\frac{D^2-1}{DV}ct\] この2つの式から、\(t'\)を消去すると、 \[\frac{ct}{D(c+V)}=Dt-\frac{D^2-1}{DV}ct\] 両辺に\(DV(c+V)/t\)を掛けます。 \[cV=D^2V(c+V)-c(D^2-1)(c+V)\] \[cV=D^2cV+D^2V^2-D^2c^2-D^2cV+c^2+cV\] \[D^2(c^2-V^2)=c^2\] \(D\gt0\)として、 \[D=\frac{1}{\sqrt{1-(V/c)^2}}\] この定数には特別な名前が付いていてローレンツ因子\(\gamma\)と言います。 先に\((\gamma^2-1)c/\gamma V\)を計算します。 \[\frac{(\gamma^2-1)c}{\gamma V}=\left(\frac{1}{1-(V/c)^2}-1\right)\frac{c}{\gamma V}\] \[=\frac{-(V/c)^2}{1-(V/c)^2}\frac{c}{\gamma V}=-\frac{V}{c}\gamma\] これを(3)式に戻してあげましょう。 \[\begin{cases}ct'=\gamma(ct)-\frac{V}{c}\gamma x\\ x'=\gamma(-Vt+x)\end{cases}\] これがローレンツ変換です。\((ct,x)=(x^0,x^1)\)とすると、 \[\begin{cases}x'^0=\gamma x^0-\frac{V}{c}\gamma x^1\\ x'^1=-\frac{V}{c}\gamma x^0+\gamma x^1\end{cases}\] となります。\(x^0\)という表記は０乗ではなく、０番目の成分という通し番号です。1変換(2乗を含まない変換)を表すのには行列が便利ですので紹介します。例として2変数から2変数に変換する1次変換を考えます。 \[\begin{cases}y^1=a^1_{\ 1}x^1+a^1_{\ 2}x^2\\y^2=a^2_{\ 1}x^1+a^2_{\ 2}x^2\end{cases}\] \(a^n_{\ m}\)は定数です。記号を増やしたくないので通し番号を振って区別してあるだけです。まずはベクトル的な表記方法に変えます。 \[\begin{pmatrix}y^1\\y^2\end{pmatrix}=\begin{pmatrix}a^1_{\ 1}x^1+a^1_{\ 2}x^2\\a^2_{\ 1}x^1+a^2_{\ 2}x^2\end{pmatrix}\] ここで行列\((a^i_{\ j})\)をこのように定義します。 \[(a^i_{\ j}):=\begin{pmatrix}a^1_{\ 1}&a^1_{\ 2}\\a^2_{\ 1}&a^2_{\ 2}\end{pmatrix}\] 行列は1次変換の定数部分を並べただけのものです、行列の計算ルールを２つ紹介します。ベクトルの右側に置くと、 \[\begin{pmatrix}a^1_{\ 1}&a^1_{\ 2}\\a^2_{\ 1}&a^2_{\ 2}\end{pmatrix}\begin{pmatrix}x^1\\x^2\end{pmatrix}:=\begin{pmatrix}a^1_{\ 1}x^1+a^1_{\ 2}x^2\\a^2_{\ 1}x^1+a^2_{\ 2}x^2\end{pmatrix}\] このように計算することにします。また \[\begin{pmatrix}ka^1_{\ 1}&ka^1_{\ 2}\\ka^2_{\ 1}&ka^2_{\ 2}\end{pmatrix}=k\begin{pmatrix}a^1_{\ 1}&a^1_{\ 2}\\a^2_{\ 1}&a^2_{\ 2}\end{pmatrix}\] 定数のくくりだし、分配ができます。１次変換\(f:(x^1,x^2)\mapsto(y^1,y^2)\)の係数を並べたものが行列\((a^{i}_{\ j})\)ですが、\(f^{-1}:(y^1,y^2)\mapsto(x^1,x^2)\)つまり逆変換の係数を並べたものを逆行列\((a^i_{\ j})^{-1}\)とします。\(2\times2\)であれば逆行列を求めることは簡単です。 \[y^1=a^1_{\ 1}x^1+a^1_{\ 2}x^2\tag{4-1}\] \[y^2=a^2_{\ 1}x^1+a^2_{\ 2}x^2\tag{4-2}\] この連立方程式を\(x^1,x^2\)について解くとこで、逆行列を得ることができます。(4-1)式\(\times a^2_{\ 2}-\)(4-2)式\(\times a^{1}_{\ 2}\)より、 \[a^2_{\ 2}y^1-a^1_{\ 2}y^2=a^1_{\ 1}a^{2}_{\ 2}x^1-a^1_{\ 2}a^{2}_{\ 1}x^1\] \[x_1=\frac{a^2_{\ 2}y^1-a^1_{\ 2}y^2}{a^1_{\ 1}a^{2}_{\ 2}-a^{1}_{\ 2}a^2_{\ 1}}\] (4-1)式\(\times a^2_{\ 1}-\)(4-2)式\(\times a^1_{\ 1}\) \[a^2_{\ 1}y^1-a^1_{\ 1}y^2=a^1_{\ 2}a^2_{\ 1}x^2-a^1_{\ 1}a^2_{\ 2}x^2\] \[x_2=\frac{-a^2_{\ 1}y^1+a^1_{\ 1}y^2}{a^1_{\ 2}a^2_{\ 2}-a^1_{\ 2}a^2_{\ 1}}\] 　以上から、 \[\begin{pmatrix}x^1\\x^2\end{pmatrix}=\begin{pmatrix}\frac{a^2_{\ 2}y^1-a^1_{\ 2}y^2}{a^1_{\ 1}a^{2}_{\ 2}-a^{1}_{\ 2}a^2_{\ 1}}\\\frac{-a^2_{\ 1}y^1+a^1_{\ 1}y^2}{a^1_{\ 2}a^2_{\ 2}-a^1_{\ 2}a^2_{\ 1}}\end{pmatrix}\] 行列の計算ルールを使うと、 \[\begin{pmatrix}x^1\\x^2\end{pmatrix}=\frac{1}{a^1_{\ 2}a^2_{\ 2}-a^1_{\ 2}a^2_{\ 1}}\begin{pmatrix}a^2_{\ 2}&-a^1_{\ 2}\\-a^2_{\ 1}&a^1_{\ 1}\end{pmatrix}\begin{pmatrix}y^1\\y^2\end{pmatrix}\] つまり逆行列は \[(a^i_{\ j})^{-1}=\frac{1}{a^1_{\ 2}a^2_{\ 2}-a^1_{\ 2}a^2_{\ 1}}\begin{pmatrix}a^2_{\ 2}&-a^1_{\ 2}\\-a^2_{\ 1}&a^1_{\ 1}\end{pmatrix}\] となります。これを利用してローレンツ変換の逆変換を求めてみましょう。ローレンツ変換をもう一度載せます。 \[\begin{pmatrix}x'^0\\x'^1\end{pmatrix}=\begin{pmatrix}\gamma x^0-\frac{V}{c}\gamma x^1\\-\frac{V}{c}\gamma x^0+\gamma x^1\end{pmatrix}\] 行列\((L^i_{\ j})\)を \[(L^i_{\ j}):=\begin{pmatrix}\gamma&-\frac{V}{c}\gamma \\-\frac{V}{c}\gamma&\gamma\end{pmatrix}\] とすればその逆行列は、 \[(L^i_{\ j})^{-1}=\frac{1}{\gamma^2-(-V\gamma/c)^2}\begin{pmatrix}\gamma&\frac{V}{c}\gamma \\\frac{V}{c}\gamma&\gamma\end{pmatrix}\] \[=\frac{\gamma^{-2}}{1-(V/c)^2}\begin{pmatrix}\gamma&\frac{V}{c}\gamma \\\frac{V}{c}\gamma&\gamma\end{pmatrix}=\begin{pmatrix}\gamma&\frac{V}{c}\gamma \\\frac{V}{c}\gamma&\gamma\end{pmatrix}\] このようにして逆変換を求めることができました。\(K(x^0,x^1)\)から速度\(V\)で遠ざかる\(K'(x'^0,x'^1)\)が変換\((L^i_{\ j})\)に対して、\(K'\)から速度\(-V\)で遠ざかる\(K\)への変換が\((L^i_{\ j})^{-1}\)です。相対速度の違い以外ないことが変換にも表れていますね。今は簡単にするため2次元で書いていましたが、ミンコフスキー空間は4次元なのでローレンツ変換は \[\begin{cases} x'^0=\gamma x^0-\frac{V}{c}\gamma x^1 \\x'^1=-\frac{V}{c}\gamma x^0+\gamma x^1 \\x'^2=x^2 \\x'^3=x^3 \end{cases}\] 逆ローレンツ変換は \[\begin{cases} x^0=\gamma x'^0+\frac{V}{c}\gamma x'^1 \\x^1=\frac{V}{c}\gamma x'^0+\gamma x'^1 \\x^2=x'^2 \\x^3=x'^3 \end{cases}\] となります。ついでになりますが、4×4の逆行列はとても複雑です。4変数から4変数の逆変換を求めなければなりません。\(a^n_{\ n}\)だけ成分を持つ行列を対角行列と言います。は簡単に逆行列を求めることができます。 \[\begin{pmatrix}a&0&0&0 \\0&b&0&0 \\0&0&c&0 \\0&0&0&d \end{pmatrix}\] こちらの対角行列を1次変換にすると \[\begin{cases}y^1=ax^1 \\y^2=bx^2 \\y^3=cx^3 \\y^4=d\ x^4 \end{cases}\] 逆変換にすると、 \[\begin{cases}x^1=1/a\ y^1 \\x^2=1/b\ y^2 \\x^3=1/c\ y^3 \\x^4=1/d\ y^4 \end{cases}\] 以上から逆行列は \[\begin{pmatrix}a&0&0&0 \\0&b&0&0 \\0&0&c&0 \\0&0&0&d \end{pmatrix}^{-1}=\begin{pmatrix}1/a&0&0&0 \\0&1/b&0&0 \\0&0&1/c&0 \\0&0&0&1/d \end{pmatrix}\] 各成分を逆数にするだけで済みます。この公式はアインシュタイン方程式を解くのに使用しますので覚えておきましょう。