今更ですが、注意点として私は縦ベクトル、横ベクトルを区別しません。スペースの都合に合わせてベクトルが縦になったり横になったりします。あまり気にしないでください。一般相対性理論で扱う時空間は物質により歪んでいます。

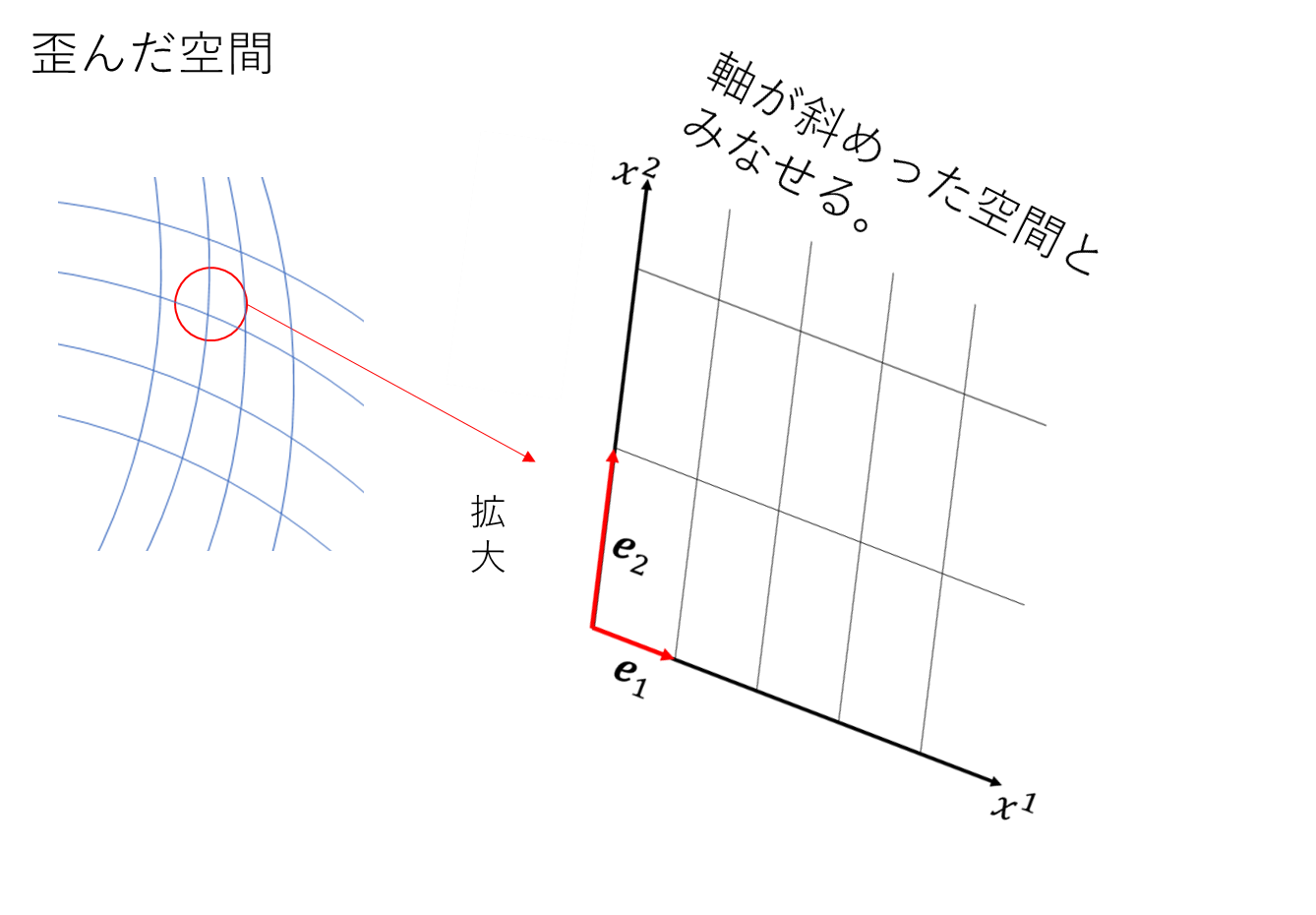
　球面を拡大すると平面とみなせるのと同じように、歪んだ空間でも拡大すると軸が斜めった空間とみなせます。いきなり歪んだ空間を扱うのは難しいので、斜めった空間での内積について知識を深めていきます。今回の話は歪んだ空間でも同じ点で定義されるベクトルについては成り立つので有効な考え方です。

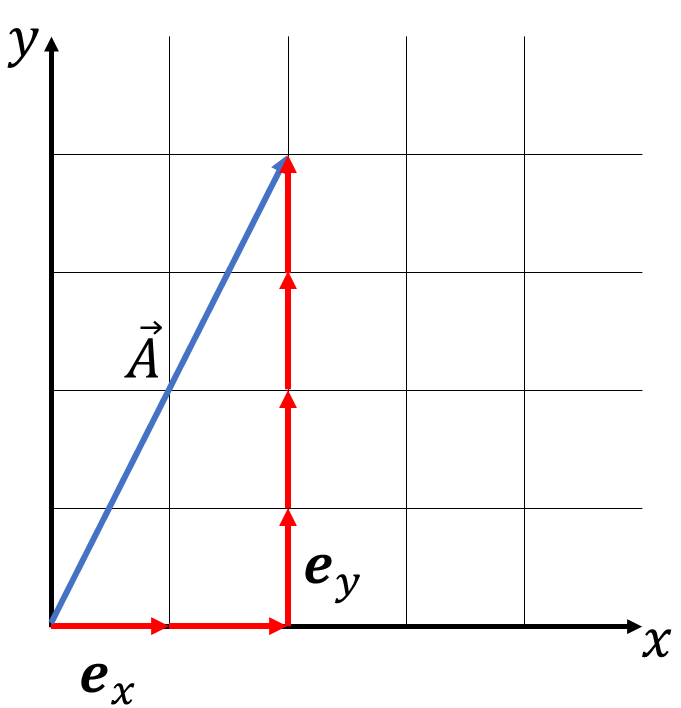
　ほとんどの方にとって復習になると思うので、簡単に済ませます。この図のベクトル\(\vec{A}=(2,4)\)はと表されます。ベクトルの計算ルールを紹介します。一般に\(\mathbb{R}^2\)直交座標のベクトル\(\vec{A}=(A^x,A^y),\vec{B}=(B^x,B^y)\)について、 \[\vec{A}+\vec{B}:=(A^x+B^x,A^y+B^y)\] 成分ごとに足し算をします。 \[k\vec{A}=k(A^x,A^y):=(kA^x,kA^y)\] ベクトルに掛けられた数\(k\)を成分に分配、くくりだしができます。２ベクトル\(\vec{A},\vec{B}\)の内積は、 \[\vec{A}\cdot\vec{B}=(A^x,A^y)\cdot(B^x,B^y):=A^xB^x+A^yB^y\] 内積はベクトルの大きさを表すのに使えます。\(\vec{A}=(2,4)\)の大きさを\(|\vec{A}|\)とすると、 \[|\vec{A}|^2=2^2+4^2=20\] これはまさに内積\(|\vec{A}|^2=\vec{A}\cdot\vec{A}\)と同じことをやっています。 また定義より交換則、分配法則も成り立ちます。 \[\vec{A}\cdot\vec{B}=A^xB^x+A^yB^y=B^xA^x+B^yA^y=\vec{B}\cdot\vec{A}\] これで交換則を示せました。 \[\vec{A}\cdot(\vec{B}+\vec{C})=(A^x,A^y)\cdot(B^x+C^x,B^y+C^y)\] \[=A^x(B^x+C^x)+A^y(B^y+C^y)\] \[=(A^xB^x+A^yB^y)+(A^xC^x+A^yC^y)=\vec{A}\cdot\vec{B}+\vec{A}\cdot\vec{C}\] 基底ベクトル \[\boldsymbol{e}_x=(1,0),\ \boldsymbol{e}_y=(0,1)\]を使うことで、\(\vec{A}=(2,4)\)は、 \[\vec{A}=(2,4)=(2,0)+(0,4)=2\boldsymbol{e}_x+4\boldsymbol{e}_y\] となります。基底ベクトルの内積は、 \[\begin{matrix}\boldsymbol{e}_x\cdot\boldsymbol{e}_x=1&\boldsymbol{e}_x\cdot\boldsymbol{e}_y=0 \\\boldsymbol{e}_y\cdot\boldsymbol{e}_x=0&\boldsymbol{e}_y\cdot\boldsymbol{e}_y=1 \end{matrix}\] なので、内積は分配法則を使って \[\vec{A}\cdot\vec{A}=(2\boldsymbol{e}_x+4\boldsymbol{e}_y)\cdot(2\boldsymbol{e}_x+4\boldsymbol{e}_y)\] \[=\boldsymbol{e}_x\cdot\boldsymbol{e}_x2^2+\boldsymbol{e}_x\cdot\boldsymbol{e}_y2\times4+\boldsymbol{e}_y\cdot\boldsymbol{e}_x4\times2+\boldsymbol{e}_y\cdot\boldsymbol{e}_y4^2\] \[\vec{A}\cdot\vec{A}=2^2+4^2=20\] とも計算できます。今は手間なだけの計算ですが、次に説明する斜交座標系で計量テンソルの導入となる計算です。このベクトル\(\vec{A}\)の内積が２０になることは覚えておいて下さい。他の座標系の例でも同じものを求めます。この記事を読み終わったら忘れていいです。

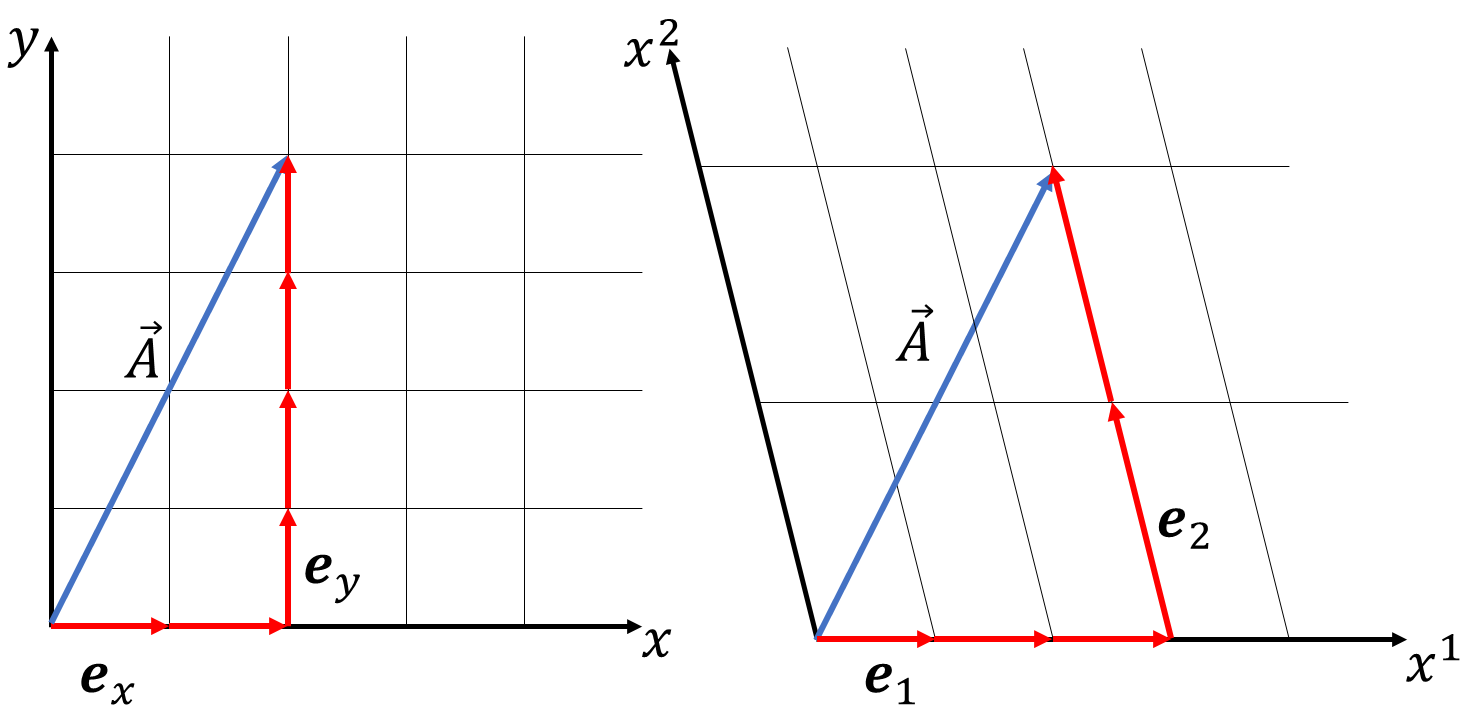
　空間のマス目は基底ベクトルによって決まるものとします。\(\mathbb{R}^2\)ユークリッド空間は、直交した２つの基底によって作られています。基底の大きさがどちらも１なので、１辺が１の正方形でした。そこで \[\boldsymbol{e}_1=(1,0),\ \boldsymbol{e}_2=(-1/2,2)\] のような基底を取ってみましょう。この基底でもベクトルを作ることができます。\(\vec{A}=(2,4)\) は、図から \[\vec{A}=(2,4)=3(1,0)+2(-1/2,2)\] と分かるので \[\vec{A}=A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2=3\boldsymbol{e}_1+2\boldsymbol{e}_2\] \((A^x,A^y)=(2,4)\)はこの斜交系では\((A^1,A^2)=(3,2)\)と表されます。ベクトルの足し算もできます。 \[\vec{A}+\vec{B}=(A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2)+(B^1\boldsymbol{e}_1+B^2\boldsymbol{e}_2)\] \[=(A^1+B^1)\boldsymbol{e}_1+(A^2+B^2)\boldsymbol{e}_2\] 成分ごとに足すというルールも一緒です。ただし内積は注意が必要です。基底ベクトルの内積を先に計算しておきます。 \[\begin{matrix}\boldsymbol{e}_1\cdot\boldsymbol{e}_1=1& \boldsymbol{e}_1\cdot\boldsymbol{e}_2=-\frac{1}{2} \\\boldsymbol{e}_2\cdot\boldsymbol{e}_1=-\frac{1}{2}& \boldsymbol{e}_2\cdot\boldsymbol{e}_2=\frac{17}{4}\end{matrix}\] 以上から内積は \[\vec{A}\cdot\vec{B}=(A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2)\cdot(B^1\boldsymbol{e}_1+B^2\boldsymbol{e}_2)\] \[=\boldsymbol{e}_1\cdot\boldsymbol{e}_1A^1B^1+\boldsymbol{e}_1\cdot\boldsymbol{e}_2A^1B^2\] \[+\boldsymbol{e}_2\cdot\boldsymbol{e}_1A^2B^1+\boldsymbol{e}_2\cdot\boldsymbol{e}_2A^2B^2\] \[\vec{A}\cdot\vec{B}=A^1B^1-\frac{1}{2}A^1B^2-\frac{1}{2}A^2B^1+\frac{17}{4}A^2B^2\] \(A^1B^1+A^2B^2\)とならないので注意です。直交系でなければ、内積は基底ベクトルにも依ることが理解できれば大丈夫です。練習として\(\vec{A}=3\boldsymbol{e}_1+2\boldsymbol{e}_2\)について\(\vec{A}\cdot\vec{A}\)を求めてみましょう。 \[\vec{A}\cdot\vec{A}=3^2-\frac{1}{2}\times3\times2-\frac{1}{2}\times2\times3+\frac{17}{4}\times2^2\] \[\vec{A}\cdot\vec{A}=9-3-3+17=20\] \(\sqrt{\vec{A}\cdot\vec{A}}\)は\(\vec{A}\)の長さになるので、直交座標でも斜交座標でも変わらないのは納得です。座標の取り方で成分は変化しますが。

　斜交系でもうまく内積を表現するために計量テンソルというものを定義します。 \[\begin{matrix}g_{11}=\boldsymbol{e}_1\cdot\boldsymbol{e}_1& g_{12}=\boldsymbol{e}_1\cdot\boldsymbol{e}_2 \\g_{21}=\boldsymbol{e}_2\cdot\boldsymbol{e}_1& g_{22}=\boldsymbol{e}_2\cdot\boldsymbol{e}_2\end{matrix}\] 計量テンソルは基底ベクトルの内積で定義されます。あまり難しく考えなくて大丈夫です。(2次元なら)ただの４つの数字の組です。計量テンソルの２つの添え字は内積をとる基底ベクトルを指定します。これにより内積は \[\vec{A}\cdot\vec{B}=(A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2)\cdot(B^1\boldsymbol{e}_1+B^2\boldsymbol{e}_2)\] \[\vec{A}\cdot\vec{B}=g_{11}A^1B^1+g_{12}A^1B^2+g_{21}A^2B^1+g_{22}A^2B^2\] となりますこれが一般的な内積の表現方法です。直交座標系での内積は計量テンソルが \[\begin{matrix}g_{xx}=1& g_{xy}=0 \\g_{yx}=0& g_{yy}=1\end{matrix}\] であった特別な場合とも言えます。

　計量テンソルを導入したことで、斜めった座標系(一様な目盛りの伸縮も可)でも内積が使えるようになりました。でもやっぱり\(A^xB^x+A^yB^y\)の形はきれいです。それを実現する双対という考え方を取り入れるため用語を整理します。まずはベクトル空間\(V\)です。 \[V:=\{A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2|A^1,A^2\in\mathbb{R}\}\] \(V\)は、実数\(A^1,A^2\)と基底ベクトル\(\boldsymbol{e}_1,\boldsymbol{e}_2\)を使って作るベクトル\(A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_1\)全体の集合を意味します。\(\boldsymbol{e}_1,\boldsymbol{e}_2\)を基底するベクトル空間\(V\)という言い方もできます。基底ベクトル\(\boldsymbol{e}_1,\boldsymbol{e}_2\)に対して \[\begin{matrix}\boldsymbol{e}_1\cdot\boldsymbol{e}^1=1& \boldsymbol{e}_1\cdot\boldsymbol{e}^2=0 \\\boldsymbol{e}_2\cdot\boldsymbol{e}^1=0& \boldsymbol{e}_2\cdot\boldsymbol{e}^2=1\end{matrix}\] を満たすベクトル\(\boldsymbol{e}^1,\boldsymbol{e}^2\)を双対基底(双対な基底ベクトル)と言います。基底ベクトルを\(\boldsymbol{e}_i=(e_{i,x},e_{i,y})\)と成分表示することにして、双対基底\(\boldsymbol{e}^1=(p,q)\)を求めてみましょう。 \[\begin{cases}\boldsymbol{e}_1\cdot\boldsymbol{e}^1=e_{1,x}\ p+e_{1,y}\ q=1 \\\boldsymbol{e}_2\cdot\boldsymbol{e}^1=e_{2,x}\ p+e_{2,y}\ q=0 \end{cases}\] これをベクトルと行列を使って表すと、 \[\begin{pmatrix}e_{1,x}&e_{1,y} \\e_{2,x}&e_{2,y}\end{pmatrix} \begin{pmatrix}p\\q\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}\] \[\boldsymbol{e}^1=\begin{pmatrix}p\\q\end{pmatrix}=\begin{pmatrix}e_{1,x}&e_{1,y} \\e_{2,x}&e_{2,y}\end{pmatrix}^{-1} \begin{pmatrix}1\\0\end{pmatrix}\] このようにして双対基底を求めます。相対性理論で双対基底を求める機会はないので覚えなくてもいいですが、逆1次変換(連立方程式を解く操作)なので双対基底の組は１つに定まることは覚えておいてください。１つに定まらないときはそもそも元々のベクトル空間の基底が独立でないなどの可能性があります。双対ベクトル空間\(V^*\)を \[V^*:=\{B_1\boldsymbol{e}^1+B_2\boldsymbol{e}^2|B_1,B_2\in\mathbb{R}\}\] と表します。実数\(B_1,B_2\)を使ったベクトル\(B_1\boldsymbol{e}^1+B_2\boldsymbol{e}^2\)の集合が双対ベクトル空間\(V^*\)ということです。双対空間の成分の添え字は下に付ける決まりになっています。双対にはとても良い性質があります。\(\vec{A}\in V,\ \vec{B}\in V^*\)の２つのベクトルの内積を取ると、 \[\vec{A}\cdot\vec{B}=(A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2)\cdot(B_1\boldsymbol{e}^1+B_2\boldsymbol{e}^2)\] \[=\boldsymbol{e}_1\cdot\boldsymbol{e}^1A^1B_1+\boldsymbol{e}_1\cdot\boldsymbol{e}^2A^1B_2\] \[+\boldsymbol{e}_2\cdot\boldsymbol{e}^1A^2B_1+\boldsymbol{e}_2\cdot\boldsymbol{e}^2A^2B_2\] \[\vec{A}\cdot\vec{B}=A^1B_1+A^2B_2\]

　例えば \[\boldsymbol{e}_1=(1,0),\ \boldsymbol{e}_2=(-1/2,2)\] と双対な基底ベクトルは \[\boldsymbol{e}^1=(1,1/4),\ \boldsymbol{e}^2=(0,1/2)\] です。

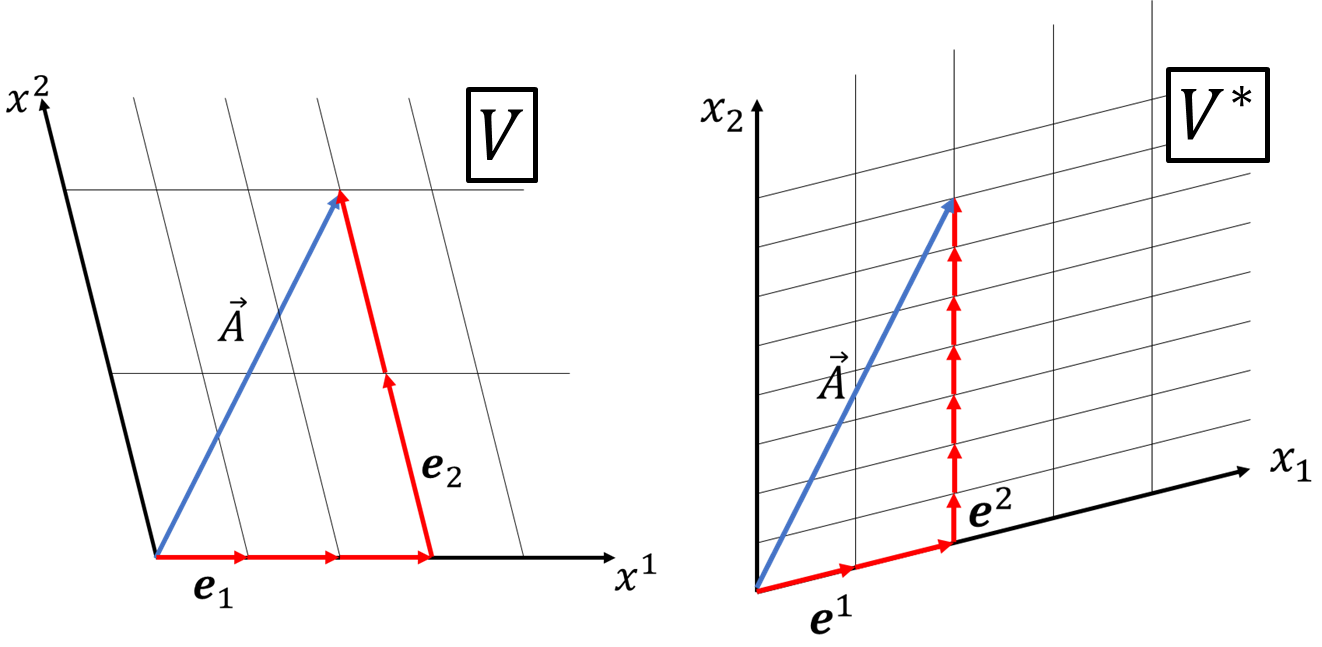
ベクトル\(\vec{A}=(2,4)\)を双対基底を使って表してみましょう。 \[\vec{A}=2(1,1/4)+7(0,1/2)\] \[\vec{A}=A_1\boldsymbol{e}^1+A_2\boldsymbol{e}^2=2\boldsymbol{e}^1+7\boldsymbol{e}^2\] \(\vec{A}\)はベクトル空間\(V\)で\((A^1,A^2)=(3,2)\)双対ベクトル空間\(V^*\)では、\((A_1,A_2)=(2,7)\)と表されることが分かりました。内積を計算してみると、 \[\vec{A}\cdot\vec{A}=A^1A_1+A^2A_2=3\times2+2\times7=20\] 結果は20となり、直交座標系で求めた内積も、計量テンソルを使っても双対を使っても結果は変わりません。

２つの公式を紹介します。まずは字上げ、字下げと言われる公式です。ベクトルはベクトル空間\(V\)とその双対ベクトル空間\(V^*\)の２つの表し方があり、 \[A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2=A_1\boldsymbol{e}^1+A_2\boldsymbol{e}^2\tag{1}\] 両辺に\(V\)の基底\(\boldsymbol{e}_1\)で内積を取ると、 \[g_{11}A^1+g_{12}A^2=A_1\] 両辺に\(\boldsymbol{e}_2\)で内積を取ると、 \[g_{21}A^1+g_{22}A^2=A_2\] これで字下げが示せました。 \[\begin{cases}g_{11}A^1+g_{12}A^2=A_1 \\g_{21}A^1+g_{22}A^2=A_2\end{cases}\] 字下げは\(V\)での計量テンソルとベクトルの成分から双対なベクトルの成分を求める公式です。(1)式に双対基底で内積を取ることで、 \[\begin{cases}A^1=g^{11}A_1+g^{12}A_2 \\A^2=g^{21}A_1+g^{22}A_2\end{cases}\] 字上げは双対空間の計量から双対空間のベクトルの成分をベクトル空間のに戻す公式です。次に計量を行列とみなすと、双対空間の計量が逆行列の関係にあるという公式です。字上げの２つの式をベクトル\((A_1,A_2)\)をベクトル\(A^1,A^2\)にする１次変換とみなすと、 \[\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}\begin{pmatrix}A^1\\A^2\end{pmatrix}=\begin{pmatrix}A_1\\A_2\end{pmatrix}\] 字上げも同様に \[\begin{pmatrix}A^1\\A^2\end{pmatrix}=\begin{pmatrix}g^{11}&g^{12}\\g^{21}&g^{22}\end{pmatrix}\begin{pmatrix}A_1\\A_2\end{pmatrix}\] 逆行列そのものですね。 \[\begin{pmatrix}g_{11}&g_{12}\\g_{21}&g_{22}\end{pmatrix}^{-1}=\begin{pmatrix}g^{11}&g^{12}\\g^{21}&g^{22}\end{pmatrix}\] が示せました。