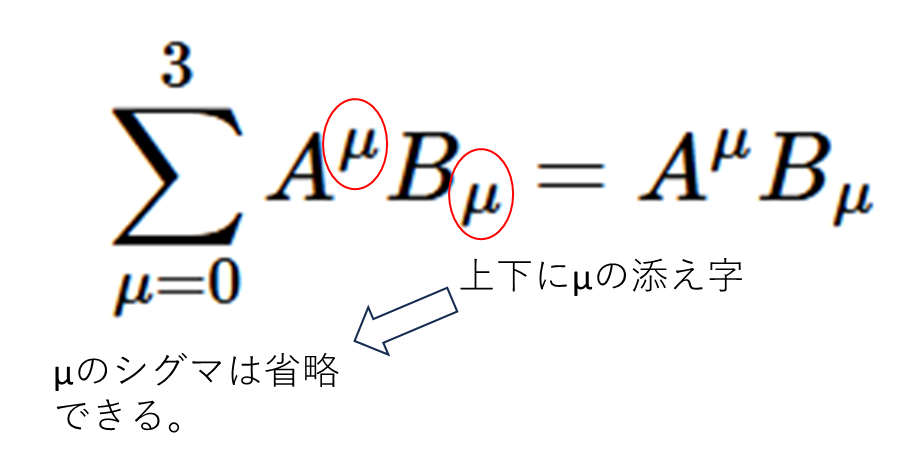楽しい科学(理論)チャンネル
歪みのない時空間をミンコフスキー空間と言います。慣性系ごとに時間の流れが違うので、共通で使えるパラメータがあると便利です。今回はそのパラメータ\(\tau\)を導入するお話です。
空間の距離

古典的な3次元空間で、点\(A(x_O,y_O,z_O)\)と点\(B(x,y,z)\)の2点間距離\(d\)は、
\[d^2=(x-x_O)^2+(y-y_O)^2+(z-z_O)^2\]
系によって長さが変わらないのは明らかですが、計算で求めるとガリレイ変換\(x\mapsto x-Vt\)を使って、
\[d^2\mapsto(x-Vt-(x_O-Vt))^2+(y-y_O)^2+(z-z_O)^2\]
\[=(x-x_O)^2+(y-y_O)^2+(z-z_O)^2\]
ガリレイ変換に依って距離が変わらないことが示せました。ミンコフスキー空間では、3次元に加えて、時間も空間の成分として考えます。ミンコフスキー空間の距離\(s\)はどのように定義すればローレンツ変換不変になるでしょうか。例えば
\[s^2:=-(x^0-x^0_O)^2+(x^1-x^1_O)^2\]
\[+(x^2-x^2_O)^2+(x^3-x^3_O)^2\]
こうです。初見ではかなり不思議な形をしていると思います。実際に点\((x^0,x^1,x^2,x^3)\)と点\((x_O^0,x_O^1,x_O^2,x_O^3)\)にローレンツ変換
\[\begin{cases}
x^0\mapsto \gamma x^0-\frac{V}{c}\gamma x^1
\\x^1\mapsto -\frac{V}{c}\gamma x^0+\gamma x^1
\\x^2\mapsto x^2
\\x^3\mapsto x^3
\end{cases}\]
をすると、
\[s^2\mapsto-\{(\gamma x^0-V\gamma/c\ x^1)-(\gamma x_O^0-V\gamma/c\ x_O^1)\}^2\]
\[+\{(-V\gamma/c\ x^0+\gamma x^1)-(-V\gamma/c\ x_O^0+\gamma x_O^1)\}^2\]
\[+(x^2-x^2_O)^2+(x^3-x^3_O)^2\]
\[=-\{\gamma(x^0-x^0_O)-V\gamma/c\ (x^1-x_O^1)\}^2\]
\[+\{-V\gamma/c\ (x^0-x^0_O)+\gamma(x^1-x_O^1)\}^2\]
\[+(x^2-x^2_O)^2+(x^3-x^3_O)^2\]
\[=-\gamma^2(1-(V/c)^2)(x^0-x^0_O)^2+\gamma^2(1-(V/c)^2)(x^1-x^1_O)^2\]
\[+(x^2-x^2_O)^2(x^3-x^3_O)^3=s^2\]
ローレンツ因子もうまく消えてミンコフスキー空間の距離はローレンツ変換で不変であることが示せました。
固有時
ローレンツ変換に依らないパラメータはミンコフスキー空間の距離\(s\)でもいいですが、時間と同じ次元にした固有時\(\tau\)というものがあります。\(\tau\)は\(s\)を光速度で割っただけです。
\[-(c\tau-c\tau_O)^2:=-(x^0-x^0_O)^2+(x^1-x^1_O)^2\]
\[+(x^2-x^2_O)^2+(x^3-x^3_O)^2\]
表記が長いので微小量で表します。\((x^0,x^1,x^2,x^3)=(x^0_O+dx^0,x^1_O+dx^1,x^2_O+dx^2,x^3_O+dx^3)\)とすると、固有時を微小量で書けます。
\[-(cd\tau)^2:=-(dx^0)^2+(dx^1)^2+(dx^2)^2+(dx^3)^2\]
\[d\tau=\frac{1}{c}\sqrt{-\{-(dx^0)^2+(dx^1)^2+(dx^2)^2+(dx^3)^2\}}\]
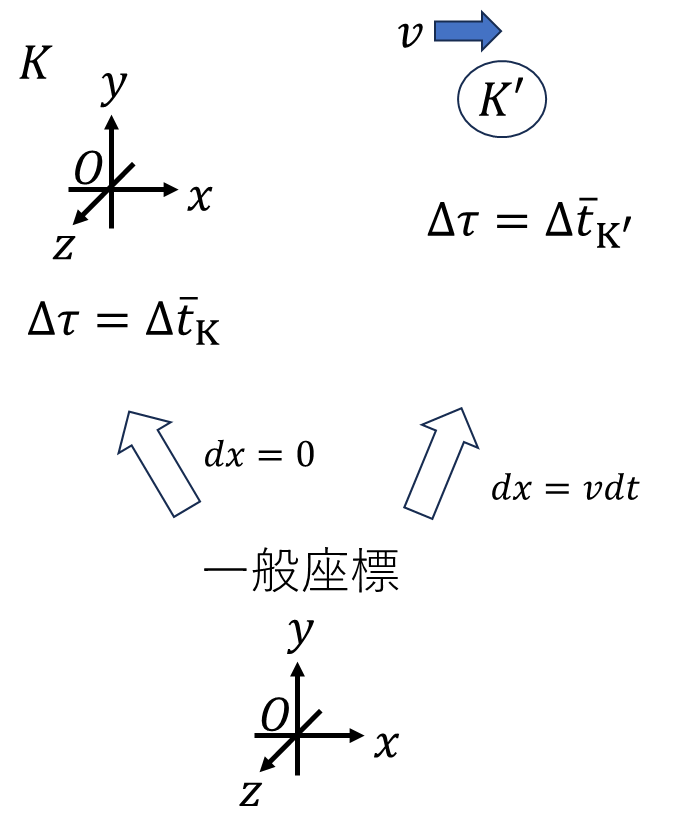
これでは固有時のイメージがわかないと思うので2つ例を出します。ただ\(K\)と速さ\(v\)で離れる\(K'\)は相対的な関係で、\(K'\)から速さ\(v\)とも見れてしまう訳です。そこで絶対的なここ目線で見ますよ。って座標を一般座標とでも名付けておきます。
まずは系\(K\)で静止している人は、\(K\)の座標系の目盛りを使って\(dx_K=dy_K=dz_K=0\)なので、
\[d\tau=\frac{1}{c}\sqrt{(dx_K^0)^2}=\frac{1}{c}cdt_K=dt_K\]
固有時と同じ時間が流れます。先ほどと同様に\(K'\)で静止する人の固有時間隔\(d\tau\)と時間間隔\(dt'\)は等しいです。
\[d\tau'=dt_{K'}\]
一般座標からみて静止系\(K\)は、\(dx=dy=dz=0\)なので、
\[dt_K=d\tau=dt\]
一般座標からみて、速度\(v\)で運動する系\(K'\)は、\(dx=vdt,dy=dz=0\)なので、
\[dt_{K'}=d\tau'=\sqrt{(cdt)^2-(vdt)^2}=\sqrt{1-(v/c)^2}dt\]
\(K\)は一般座標の時間間隔と同じ時間間隔であるのに対して、\(\sqrt{1-(v/c)^2}\lt1\)なので、一般座標に比べて\(K'\)の方が時間が遅れています。また、2つの式から\(dt\)を消去すると、
\[\frac{\varDelta t_{K'}}{\varDelta t_K}=\sqrt{1-(v/c)^2}\lt1\]
\[\varDelta t_{K'}\lt \varDelta t_{K}\]
(dを変化量のつもりで使ってましたが、分数にしたら微分みたいになったので、変化量を\(\varDelta\)にしました。)絶対的な座標を取らなくても動いている方が時間が遅れるということがこの不等式から分かります。
逆に時間はそれぞれの慣性系で流れ方が違いますが、
\[d\tau=\sqrt{1-(v/c)^2}dt\]
として、どの系でも同じになるように、\(\sqrt{1-(v/c)^2}\)で補正を取った時間が固有時というイメージでよいでしょう。また物体の速度は光速度\(c\)を超えません。なぜなら固有時が虚数になってしまうためです。
ミンコフスキー空間の計量
ミンコフスキー空間の計量を距離をヒントに考えていきます。3次元空間の距離\(d\)を
\[d^2=(\varDelta x)^2+(\varDelta y)^2+(\varDelta z)^2\tag{1}\]
と表すことにしましょう。線素ベクトル\(\varDelta \vec{x}=\varDelta x\boldsymbol{e}_x+\varDelta y\boldsymbol{e}_y+\varDelta z\boldsymbol{e}_z\)の内積ともみなせるので、
\[d^2=\varDelta \vec{x}\cdot\varDelta \vec{x}\]
\[=g_{xx}\varDelta x\varDelta x+g_{xy}\varDelta x\varDelta y+g_{xz}\varDelta x\varDelta z\]
\[+g_{yx}\varDelta y\varDelta x+g_{yy}\varDelta y\varDelta y+g_{yz}\varDelta y\varDelta z\]
\[+g_{zx}\varDelta z\varDelta x+g_{zy}\varDelta z\varDelta y+g_{zz}\varDelta z\varDelta z\tag{2}\]
(2)式の計量テンソルを調整して(1)式になればいいので3次元直交座標での計量テンソルは、
\[\begin{matrix}g_{xx}=1& g_{xy}=0&g_{xz}=0
\\g_{yx}=0& g_{yy}=1&g_{yz}=0
\\g_{zx}=0& g_{zy}=0&g_{zz}=1\end{matrix}\]
となります。同じ考察からミンコフスキー空間の計量を求めましょう。ミンコフスキー空間の距離\(s\)は
\[s^2=-(\varDelta x^0)^2+(\varDelta x^1)^2+(\varDelta x^2)^2+(\varDelta x^3)^2\tag{3}\]
時空間の線素ベクトル
\[\varDelta \vec{x}=\varDelta x^0\boldsymbol{e}_0+\varDelta x^1\boldsymbol{e}_1+\varDelta x^2\boldsymbol{e}_2+\varDelta x^3\boldsymbol{e}_3\]
の内積として距離を求めると、
\[s^2=\varDelta \vec{x}\cdot\varDelta \vec{x}\]
\[=g_{00}\varDelta x^0\varDelta x^0+g_{01}\varDelta x^0\varDelta x^1+g_{02}\varDelta x^0\varDelta x^2+g_{03}\varDelta x^0\varDelta x^3\]
\[+g_{10}\varDelta x^1\varDelta x^0+g_{11}\varDelta x^1\varDelta x^1+g_{12}\varDelta x^1\varDelta x^2+g_{13}\varDelta x^1\varDelta x^3\]
\[+g_{20}\varDelta x^2\varDelta x^0+g_{21}\varDelta x^2\varDelta x^1+g_{22}\varDelta x^2\varDelta x^2+g_{23}\varDelta x^2\varDelta x^3\]
\[+g_{30}\varDelta x^3\varDelta x^0+g_{31}\varDelta x^3\varDelta x^1+g_{32}\varDelta x^3\varDelta x^2+g_{33}\varDelta x^3\varDelta x^3\tag{4}\]
(3)式、(4)式の比較から計量テンソルは
\[\begin{matrix}g_{00}=-1& g_{01}=0&g_{02}=0&g_{03}=0
\\g_{10}=0& g_{11}=1&g_{12}=0&g_{13}=0
\\g_{20}=0& g_{21}=0&g_{22}=1&g_{23}=0
\\g_{30}=0& g_{31}=0&g_{32}=0&g_{33}=1\end{matrix}\]
さすがに4次元だと計量テンソルは16個の成分になり多いですね。
アインシュタインの縮約記法
ちょっと話が変わりますが、相対性理論では4次元を考えなくてはなりません。ミンコフスキー空間の位置ベクトルは
\[\vec{x}=x^0\boldsymbol{e}_0+x^1\boldsymbol{e}_1+x^2\boldsymbol{e}_2+x^3\boldsymbol{e}_3\]
これくらいならいいですが、後でリーマン曲率テンソルという4階テンソルという\(256\)個の成分をもつテンソルも出てきます。当然式もとても長くなってしまいます。これを解決してくれるのがアインシュタインの縮約記法です。今回は位置ベクトル\(\vec{x}\)と固有時の微小量\(d\tau\)を縮約記法を使って表してみます。まずは位置と固有時を総和の記号を使って表してみましょう。
\[\vec{x}=x^0\boldsymbol{e}_0+x^1\boldsymbol{e}_1+x^2\boldsymbol{e}_2+x^3\boldsymbol{e}_3\]
\[\vec{x}=\sum_{\mu=0}^3x^\mu\boldsymbol{e}_\mu\]
固有時は
\[-(cd\tau)^2=-(dx^0)^2+(dx^1)^2+(dx^2)^2+(dx^3)^2\]
\[=g_{00}dx^0dx^0+g_{01}dx^0dx^1+g_{02}dx^0dx^2+g_{03}dx^0dx^3\]
\[+g_{10}dx^1dx^0+g_{11}dx^1dx^1+g_{12}dx^1dx^2+g_{13}dx^1dx^3\]
\[+g_{20}dx^2dx^0+g_{21}dx^2dx^1+g_{22}dx^2dx^2+g_{23}dx^2dx^3\]
\[+g_{30}dx^3dx^0+g_{31}dx^3dx^1+g_{32}dx^3dx^2+g_{33}dx^3dx^3\]
\[=\sum_{\mu=0}^3g_{\mu0}dx^\mu dx^0+g_{\mu1}dx^\mu dx^1+g_{\mu2}dx^\mu dx^2+g_{\mu3}dx^\mu dx^3\]
もう1回総和の記号を使えますね。
\[-(cd\tau)^2=\sum_{\mu=0}^3\sum_{\nu=0}^3g_{\mu\nu}dx^\mu dx^\nu\]
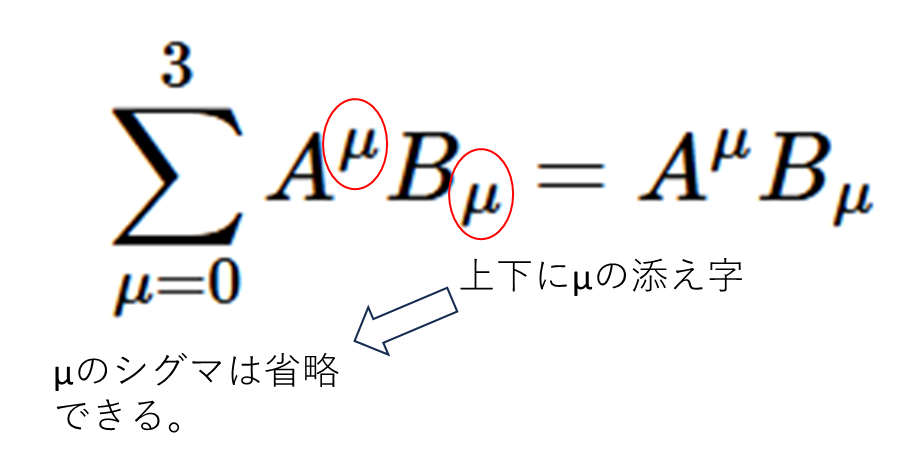
ここでアインシュタインの縮約記法というものを取り入れます。使い方は簡単です。上下に同じ添え字があればそれに関する総和の記号を省略します。これにより位置ベクトルは、
\[\vec{x}=x^\mu\boldsymbol{e}_\mu\]
固有時は
\[-(cd\tau)^2=g_{\mu\nu}dx^\mu dx^\nu\]
\[d\tau=\frac{1}{c}\sqrt{-g_{\mu\nu}dx^\mu dx^\nu}\]
となります。とてもシンプルですね。しかしこの記法は添え字に関していくつ分足していいのかが書いていません。そこは文脈から推測しなくてはなりません。ちなみに添え字は何を使ってもいいです。結局は数字が入るので、元の添え字が何であれ同じことです。
\[A^\mu B_\mu=A^0B_0+A^1B_1+A^2B_2+A^3B_3\]
\[A^i B_i=A^0B_0+A^1B_1+A^2B_2+A^3B_3\]
4元速度\(u^\mu\)
ミンコフスキー空間の位置を移動する速さを表す物理量が欲しいですね。そこで、考えられたのが4元速度\(u^\mu\boldsymbol{e}_\mu\)です。
\[u^\mu\boldsymbol{e}_\mu:=\frac{dx^\mu}{d\tau}\boldsymbol{e}_\mu\]
4元速度の成分\(u^\mu\)は、位置\(x^\mu\)の固有時微分で定義します。これを成分ごとに書くと、
\[(u^0,u^1,u^2,u^3)=\left(\frac{dx^0}{d\tau},\frac{dx^1}{d\tau},\frac{dx^2}{d\tau},\frac{dx^3}{d\tau}\right)\]
こうなります。4元速度は我々の3次元の物理量を使うとどのように見えるか見てみます。運動している物体の速度を\(v^i\boldsymbol{e}_i=(v^x,v^y,v^z)\)とします。空間成分はどれも一緒なのでまとめて計算します。固有時は\(d\tau=\sqrt{1-(v/c)^2}dt\)ともかけるので、
\[(u^0,u^i)=\left(\frac{c}{\sqrt{1-(v/c)^2}}\frac{dt}{dt},\frac{1}{\sqrt{1-(v/c)^2}}\frac{dx^i}{dt}\right)\]
\[(u^0,u^i)=\left(\frac{c}{\sqrt{1-(v/c)^2}},\frac{v^i}{\sqrt{1-(v/c)^2}}\right)\]
4元速度の時間成分は\(c\)を\(\sqrt{1-(v/c)^2}\)で割った量、空間成分は\(v^i\)を\(\sqrt{1-(v/c)^2}\)で割った量になっています。光のより遅ければニュートン力学的速度ですが、光速度に近づけると急激にでかくなって発散するのが4元速度ですね。3次元空間での等速直線運動(直進)が4元速度\(u^\mu\boldsymbol{e}_\mu\)を使ってどう記述されるか見てみます。3次元的には
\[\frac{d\vec{v}}{dt}=\boldsymbol{0}\]
または\(\vec{v}=\mathrm{\boldsymbol{const.}}\)が等速直線運動を表す式です。4元速度\((u^0,u^i)\)を固有時で微分してみます。
\[\frac{d}{d\tau}(u^0,u^i)=\frac{d}{d\tau}\left(\frac{c}{\sqrt{1-(v/c)^2}},\frac{v^i}{\sqrt{1-(v/c)^2}}\right)\]
\[=\frac{1}{\sqrt{1-(v/c)^2}}\frac{d}{dt}\left(\frac{c}{\sqrt{1-(v/c)^2}},\frac{v^i}{\sqrt{1-(v/c)^2}}\right)\]
光速度\(c\)は定数です。等速直線運動なので、\(v,v^i\)も定数なので、時間的に変化せず、微分の結果は0になります。
\[\frac{d}{d\tau}(u^\mu\boldsymbol{e}_\mu)=\boldsymbol{0}\]
時空間で見ても4元速度が一定なので覚えやすいですね。