いよいよ歪んだ空間でのお話です。歪んだ空間では平行移動が面倒なのもありますが、何よりそのせいでベクトルの微分が今まで通りにいきません。

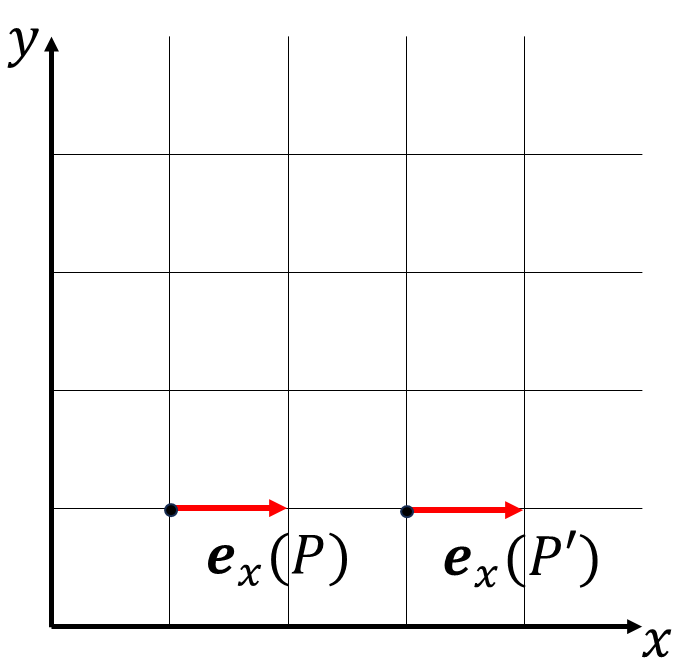
斜交系(直交座標も含む)では、基底ベクトルはどの点でも同じベクトルとして表すことができます。任意の２点\(P,P'\)について、 \[\boldsymbol{e}_x(P)=\boldsymbol{e}_x(P'),\ \boldsymbol{e}_x(P)-\boldsymbol{e}_x(P')=\boldsymbol{0}\] が成り立ちます。\(P,P'\)の距離を\(\delta x\)とします。両辺を\(\delta x\)で割ります。 \[\frac{\boldsymbol{e}_x(P)-\boldsymbol{e}_x(P')}{\delta x}=\boldsymbol{0}\] \(\delta x\)を十分に小さければ微分とみなせて \[\frac{\partial\boldsymbol{e_x}}{\partial x}=\boldsymbol{0}\] と基底ベクトルは定ベクトルだったわけです。

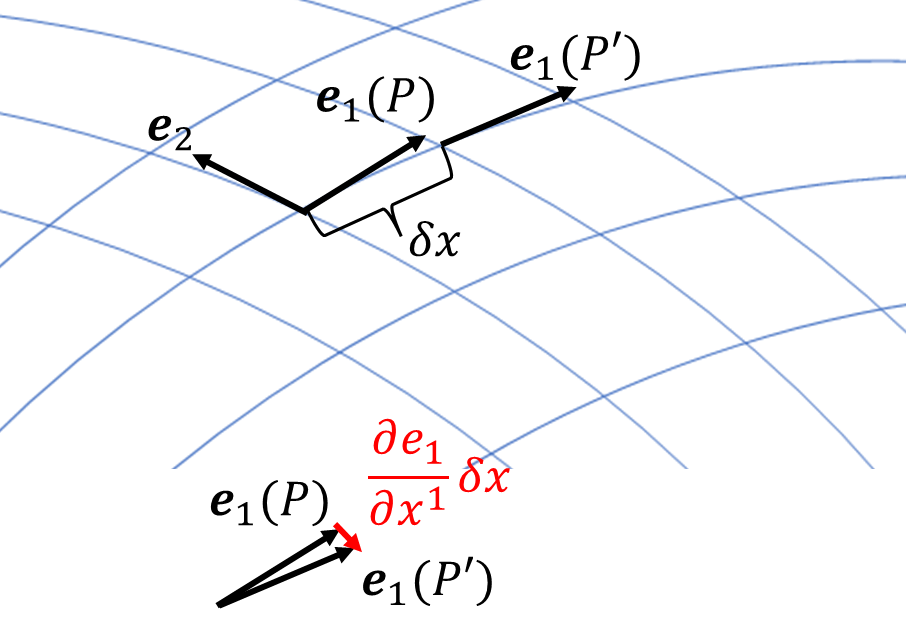
歪んだ空間ではそもそも軸が曲がっているので、基底ベクトルを軸に平行なベクトルと定義した場合基準点によって基底ベクトルが変化します。具体的には点\(P\)での\(x^1\)軸方向の基底ベクトル\(\boldsymbol{e}_1(P)\)、と\(x^1\)方向に\(\delta x\)だけずれた点\(P'\)での\(x^1\)軸方向の基底ベクトル\(\boldsymbol{e}_1(P')\)は一致しません。 \[\boldsymbol{e}_1(P)\neq\boldsymbol{e}_1(P')\] この式を左辺に移行して\(\delta x\)で割ると \[\frac{\boldsymbol{e}_1(P')-\boldsymbol{e}_1(P)}{\delta x}\neq\boldsymbol{0}\] こうなります。\(\delta x\)が十分に小さければ基底ベクトルの微分とみなせるので、基底ベクトルの微分も何かしらのベクトルになることがこの考察から分かります。一般にあるベクトル\(\vec{A}=A^1\boldsymbol{e}_1+A^2\boldsymbol{e}_2\)の微分は \[\frac{\partial \vec{A}}{\partial x^i}=\frac{\partial A^1}{\partial x^i}\boldsymbol{e}_1+A^1\frac{\partial \boldsymbol{e}_1}{\partial x^i}+\frac{\partial A^2}{\partial x^i}\boldsymbol{e}_2+A^2\frac{\partial \boldsymbol{e}_2}{\partial x^i}\] このようになります。もう複雑そうなにおいがしますが、その通りです。微分結果も成分ごとに書くことができません。 しかしそれでは成分ごとに計算できるベクトルの良さが発揮されません。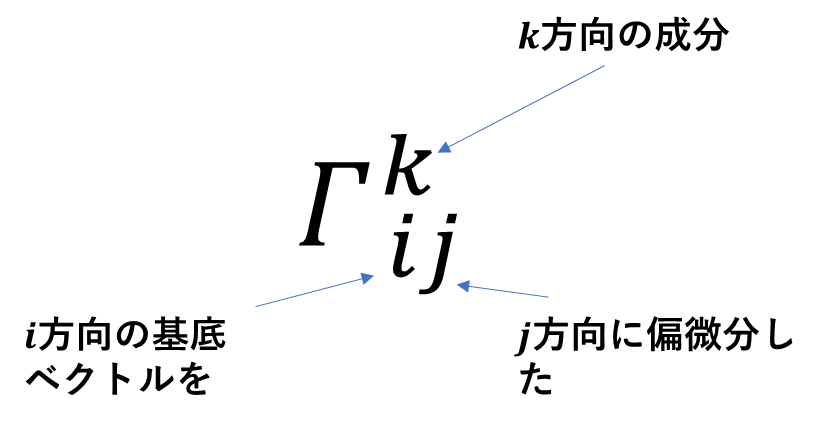 \[\frac{\partial \boldsymbol{e}_1}{\partial x^2}=\left(\frac{\partial \boldsymbol{e}_1}{\partial x^2}の第1成分,\frac{\partial \boldsymbol{e}_1}{\partial x^2}の第2成分\right)\] このよう基底ベクトルの偏微分も成分ごとに計算結果を得たいところです。そこで考えられたのがクリストッフェルの記号\(\Gamma^k_{\ ij}\)です。\(i\)方向の基底ベクトルを\(j\)方向に微分した\(k\)方向の成分と覚えておきましょう。

　例えば\(\partial\boldsymbol{e}_1\)の\(x^2\)方向の偏微分は \[\frac{\partial\boldsymbol{e}_1}{\partial x^2}=\Gamma^1_{\ 12}\boldsymbol{e}_1+\Gamma^2_{\ 12}\boldsymbol{e}_2\] このように計算されます。クリストッフェルの記号の正体についてはまた今度見ていきましょう。

　等価原理を覚えているでしょうか。この図でもう一度簡単に説明すると、地球の中心\(K'\)にいれば太陽\(K'\)からの重力の影響を受けないということです。逆も同様です。\(K'\)は局所的(地球の中心)に慣性系とみなせるので、地球は一定の４元速度\(u'^\mu\boldsymbol{e}'_\mu\)で進みます。固有時微分は０になるはずです。 \[\frac{d}{d\tau}(u'^\mu\boldsymbol{e}'_\mu)=\boldsymbol{0}\] 一般相対性原理に依れば、加速度系\(K\)でも時空が歪んでいるだけで物理法則の形は同じなので、\(K\)からみた地球の4元速度を\(u^\mu\boldsymbol{e}_\mu\)とすると、太陽\(K\)での地球の運動は \[\frac{d}{d\tau}(u^\mu\boldsymbol{e}_\mu)=\boldsymbol{0}\] となります。成分ごとに書き出します。 \[\frac{d}{d\tau}(u^0\boldsymbol{e}_0+u^1\boldsymbol{e}_1+u^2\boldsymbol{e}_2+u^3\boldsymbol{e}_3)=\boldsymbol{0}\] 基底ベクトルも微分を受けうることに注意して、 \[\frac{du^0}{d\tau}\boldsymbol{e}_0+\frac{du^1}{d\tau}\boldsymbol{e}_1+\frac{du^2}{d\tau}\boldsymbol{e}_2+\frac{du^3}{d\tau}\boldsymbol{e}_3\] \[+u^0\frac{d\boldsymbol{e}_0}{d\tau}+u^1\frac{d\boldsymbol{e}_1}{d\tau}+u^2\frac{d\boldsymbol{e}_2}{d\tau}+u^3\frac{d\boldsymbol{e}_3}{d\tau}=\boldsymbol{0}\tag{1}\] 基底ベクトルを位置の関数と見ます。(正確にはベクトル場)\(\boldsymbol{e}_\xi(x^0(\tau),x^1(\tau),x^2(\tau),x^3(\tau))\)位置はパラメータ\(\tau\)で決まるので、合成関数の微分を使います。計算量が多いですが全ての成分について同じ計算をするので、\(0,1,2,3\)成分を纏めて計算します。 \[\frac{d\boldsymbol{e}_\xi}{d\tau}=\frac{\partial \boldsymbol{e}_\xi}{\partial x^0}\frac{dx^0}{d\tau}+\frac{\partial \boldsymbol{e}_\xi}{\partial x^1}\frac{dx^1}{d\tau}+\frac{\partial \boldsymbol{e}_\xi}{\partial x^2}\frac{dx^2}{d\tau}+\frac{\partial \boldsymbol{e}_\xi}{\partial x^3}\frac{dx^3}{d\tau}\] \[\frac{d\boldsymbol{e}_\xi}{d\tau}=\frac{\partial \boldsymbol{e}_\xi}{\partial x^0}u^0+\frac{\partial \boldsymbol{e}_\xi}{\partial x^1}u^1+\frac{\partial \boldsymbol{e}_\xi}{\partial x^2}u^2+\frac{\partial \boldsymbol{e}_\xi}{\partial x^3}u^3\] 基底ベクトルの偏微分を全てクリストッフェルの記号を使って表します。４次元空間の基底ベクトルなので、偏微分した結果も４次元のベクトルになることに注意して、 \[\frac{d\boldsymbol{e}_\xi}{d\tau}=(\Gamma^0_{\ \xi0}\boldsymbol{e}_0+\Gamma^1_{\ \xi0}\boldsymbol{e}_1+\Gamma^2_{\ \xi0}\boldsymbol{e}_2+\Gamma^3_{\ \xi0}\boldsymbol{e}_3)u^0\] \[+(\Gamma^0_{\ \xi1}\boldsymbol{e}_0+\Gamma^1_{\ \xi1}\boldsymbol{e}_1+\Gamma^2_{\ \xi1}\boldsymbol{e}_2+\Gamma^3_{\ \xi1}\boldsymbol{e}_3)u^1\] \[+(\Gamma^0_{\ \xi2}\boldsymbol{e}_0+\Gamma^1_{\ \xi2}\boldsymbol{e}_1+\Gamma^2_{\ \xi2}\boldsymbol{e}_2+\Gamma^3_{\ \xi2}\boldsymbol{e}_3)u^2\] \[+(\Gamma^0_{\ \xi3}\boldsymbol{e}_0+\Gamma^1_{\ \xi3}\boldsymbol{e}_1+\Gamma^2_{\ \xi3}\boldsymbol{e}_2+\Gamma^3_{\ \xi3}\boldsymbol{e}_3)u^3\] 展開して基底ベクトルごとに並び変えます。 \[\frac{d\boldsymbol{e}_\xi}{d\tau}=\sum_{\rho=0}^3\Gamma_{\ \xi\rho}^0u^\rho\boldsymbol{e}_0+\sum_{\rho=0}^3\Gamma_{\ \xi\rho}^1u^\rho\boldsymbol{e}_1+\sum_{\rho=0}^3\Gamma_{\ \xi\rho}^2u^\rho\boldsymbol{e}_2+\sum_{\rho=0}^3\Gamma_{\ \xi\rho}^3u^\rho\boldsymbol{e}_3\] 縮約記法により\(\sum\)を省略して\(\xi=0,1,2,3\)を順番に入れて(1)に代入します。 \[\frac{du^0}{d\tau}\boldsymbol{e}_0+\frac{du^1}{d\tau}\boldsymbol{e}_1+\frac{du^2}{d\tau}\boldsymbol{e}_2+\frac{du^3}{d\tau}\boldsymbol{e}_3\] \[+u^0(\Gamma_{\ 0\rho}^0u^\rho\boldsymbol{e}_0+\Gamma_{\ 0\rho}^1u^\rho\boldsymbol{e}_1+\Gamma_{\ 0\rho}^2u^\rho\boldsymbol{e}_2+\Gamma_{\ 0\rho}^3u^\rho\boldsymbol{e}_3)\] \[+u^1(\Gamma_{\ 1\rho}^0u^\rho\boldsymbol{e}_0+\Gamma_{\ 1\rho}^1u^\rho\boldsymbol{e}_1+\Gamma_{\ 1\rho}^2u^\rho\boldsymbol{e}_2+\Gamma_{\ 1\rho}^3u^\rho\boldsymbol{e}_3)\] \[+u^2(\Gamma_{\ 2\rho}^0u^\rho\boldsymbol{e}_0+\Gamma_{\ 2\rho}^1u^\rho\boldsymbol{e}_1+\Gamma_{\ 2\rho}^2u^\rho\boldsymbol{e}_2+\Gamma_{\ 2\rho}^3u^\rho\boldsymbol{e}_3)\] \[+u^3(\Gamma_{\ 3\rho}^0u^\rho\boldsymbol{e}_0+\Gamma_{\ 3\rho}^1u^\rho\boldsymbol{e}_1+\Gamma_{\ 3\rho}^2u^\rho\boldsymbol{e}_2+\Gamma_{\ 3\rho}^3u^\rho\boldsymbol{e}_3)=\boldsymbol{0}\] 展開して基底ベクトルごとに並び変えます。 \[\left(\frac{du^0}{d\tau}+\Gamma_{\ 0\rho}^0u^0u^\rho+\Gamma_{\ 1\rho}^0u^1u^\rho+\Gamma_{\ 2\rho}^0u^2u^\rho+\Gamma_{\ 3\rho}^0u^3u^\rho\right)\boldsymbol{e}_0\] \[+\left(\frac{du^1}{d\tau}+\Gamma_{\ 0\rho}^1u^0u^\rho+\Gamma_{\ 1\rho}^1u^1u^\rho+\Gamma_{\ 2\rho}^1u^2u^\rho+\Gamma_{\ 3\rho}^1u^3u^\rho\right)\boldsymbol{e}_1\] \[+\left(\frac{du^2}{d\tau}+\Gamma_{\ 0\rho}^2u^0u^\rho+\Gamma_{\ 1\rho}^2u^1u^\rho+\Gamma_{\ 2\rho}^2u^2u^\rho+\Gamma_{\ 3\rho}^2u^3u^\rho\right)\boldsymbol{e}_2\] \[+\left(\frac{du^3}{d\tau}+\Gamma_{\ 0\rho}^3u^0u^\rho+\Gamma_{\ 1\rho}^3u^1u^\rho+\Gamma_{\ 2\rho}^3u^2u^\rho+\Gamma_{\ 3\rho}^3u^3u^\rho\right)\boldsymbol{e}_3=\boldsymbol{0}\] 上下でそろった添え字があるのでもう一回縮約記法が使えますね。 \[\left(\frac{du^0}{d\tau}+\Gamma_{\ \nu\rho}^0u^\nu u^\rho\right)\boldsymbol{e}_0+\left(\frac{du^1}{d\tau}+\Gamma_{\ \nu\rho}^1u^\nu u^\rho\right)\boldsymbol{e}_1\] \[+\left(\frac{du^2}{d\tau}+\Gamma_{\ \nu\rho}^2u^\nu u^\rho\right)\boldsymbol{e}_2+\left(\frac{du^3}{d\tau}+\Gamma_{\ \nu\rho}^3u^\nu u^\rho\right)\boldsymbol{e}_3=\boldsymbol{0}\] かなりすっきりしました。全ての成分が０ベクトルにならければならないので任意の\(\mu=0,1,2,3\)成分について \[\frac{du^\mu}{d\tau}+\Gamma_{\ \nu\rho}^\mu u^\nu u^\rho=0\] が成り立ちます。この方程式を測地線方程式と言います。重力場での惑星の軌跡を表す方程式です。この式の本質は、局所慣性系での直進を座標変換により一般座標で表したということにあります。