クリストッフェルの記号の下の２つの添え字は交換できます。それを示すために基底ベクトルと偏微分の関係性について知る必要があります。ある小さい領域で曲面\((x^1,x^2)\)に接面を取ります。その接面を直交座標系\((x,y)\)で表します。上手い図が掛けませんでしたが、ある点\(P\)で\(\boldsymbol{e}_1,\boldsymbol{e}_2\)を含む平面を取り、\(P\)を原点とする直交座標\(x,y\)を取るということです。

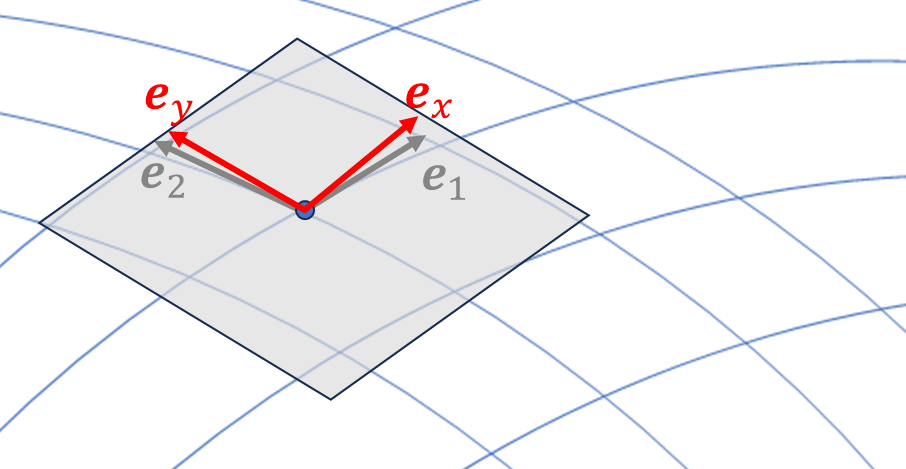
曲面の点\(P\)での線素ベクトル\(d\vec{x}\)を \[d\vec{x}=dx^1\ \boldsymbol{e}_1+dx^2\ \boldsymbol{e}_2\] と表すことにしましょう。接平面では \[d\vec{x}=dx\ \boldsymbol{e}_x+dy\ \boldsymbol{e}_y\] と表すことができます。これを微分の計算手法を使って\(\boldsymbol{e}_1,\boldsymbol{e}_2\)で表していきます。 \[dx=\frac{\partial x}{\partial x^1}dx^1+\frac{\partial x}{\partial x^2}dx^2\] \[dy=\frac{\partial y}{\partial x^1}dx^1+\frac{\partial y}{\partial x^2}dx^2\] 直交座標系の微小量はこのように座標変換されるので、 \[d\vec{x}=\left(\frac{\partial x}{\partial x^1}dx^1+\frac{\partial x}{\partial x^2}dx^2\right)\boldsymbol{e}_x+\left(\frac{\partial y}{\partial x^1}dx^1+\frac{\partial y}{\partial x^2}dx^2\right)\boldsymbol{e}_y\] \[=dx^1\left(\frac{\partial x}{\partial x^1}\boldsymbol{e}_x+\frac{\partial y}{\partial x^1}\boldsymbol{e}_y\right)+dx^2\left(\frac{\partial x}{\partial x^2}\boldsymbol{e}_x+\frac{\partial y}{\partial x^2}\boldsymbol{e}_y\right)\] \[=dx^1\ \frac{\partial}{\partial x^1}(x,y)+dx^2\ \frac{\partial}{\partial x^2}(x,y)\] 斜交座標系では、微小量ベクトル\(d\vec{x}\)は \[d\vec{x}=dx^1\ \boldsymbol{e}_1+dx^2\ \boldsymbol{e}_1\] と表されるはずなので、 \[\boldsymbol{e}_1=\frac{\partial}{\partial x^1}(x,y),\ \boldsymbol{e}_2=\frac{\partial}{\partial x^2}(x,y)\] \(x^i\)方向の基底ベクトルは、変換前の座標に\(x^i\)の偏微分を作用させたものともとらえられます。 \[\frac{\partial \boldsymbol{e}_\mu}{\partial x^\nu}=:\Gamma_{\ \mu\nu}^\xi\boldsymbol{e}_\xi\] これがクリストッフェルの記号の定義です。\(\xi\)には縮約がかかっているので具体的に４次元では、 \[\frac{\partial \boldsymbol{e}_\mu}{\partial x^\nu}=\Gamma_{\ \mu\nu}^0\boldsymbol{e}_0+\Gamma_{\ \mu\nu}^1\boldsymbol{e}_1+\Gamma_{\ \mu\nu}^2\boldsymbol{e}_2+\Gamma_{\ \mu\nu}^3\boldsymbol{e}_3\] です。先ほど示した基底ベクトルの正体から、 \[\Gamma_{\ \mu\nu}^\xi\boldsymbol{e}_\xi=\frac{\partial }{\partial x^\nu}\boldsymbol{e}_\mu=\frac{\partial }{\partial x^\nu}\frac{\partial }{\partial x^\mu}(x,y)\] 偏微分の順番を交換すると、 \[=\frac{\partial }{\partial x^\mu}\frac{\partial }{\partial x^\nu}(x,y)=\frac{\partial }{\partial x^\mu}\boldsymbol{e}_\nu=\Gamma_{\ \nu\mu}^\xi\boldsymbol{e}_\xi\] これでクリストッフェルの記号の下の２つの添え字が交換できることを示せました。(示せましたっていうよりそのような性質をもつ曲面を扱うと言った方が正しいかもしれません。)基底ベクトルと偏微分の添え字が交換できることもついでに示せました。

　クリストッフェルの記号を計量テンソルを使って表します。 \[\frac{\partial \boldsymbol{e}_\mu}{\partial x^\nu}=\Gamma_{\ \mu\nu}^0\boldsymbol{e}_0+\Gamma_{\ \mu\nu}^1\boldsymbol{e}_1+\Gamma_{\ \mu\nu}^2\boldsymbol{e}_2+\Gamma_{\ \mu\nu}^3\boldsymbol{e}_3\] まずはクリストッフェルの記号からスタートします。この式の両辺にそれぞれの基底ベクトル\(\boldsymbol{e}_0,\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3\)の内積を取り４つの式を得ます。 \[\begin{cases} \boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu=g_{00}\Gamma_{\ \mu\nu}^0+g_{01}\Gamma_{\ \mu\nu}^1+g_{02}\Gamma_{\ \mu\nu}^2+g_{03}\Gamma_{\ \mu\nu}^3 \\\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu=g_{10}\Gamma_{\ \mu\nu}^0+g_{11}\Gamma_{\ \mu\nu}^1+g_{12}\Gamma_{\ \mu\nu}^2+g_{13}\Gamma_{\ \mu\nu}^3 \\\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu=g_{20}\Gamma_{\ \mu\nu}^0+g_{21}\Gamma_{\ \mu\nu}^1+g_{22}\Gamma_{\ \mu\nu}^2+g_{23}\Gamma_{\ \mu\nu}^3 \\\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu=g_{30}\Gamma_{\ \mu\nu}^0+g_{31}\Gamma_{\ \mu\nu}^1+g_{32}\Gamma_{\ \mu\nu}^2+g_{33}\Gamma_{\ \mu\nu}^3 \end{cases}\] 偏微分の記号\(\partial/\partial x^\nu=\partial_\nu\)と省略しています。気づいたでしょうか、クリストッフェルの記号をベクトル、計量テンソルを行列とみることができますね。 \[\begin{pmatrix} \boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu\end{pmatrix} =\begin{pmatrix}g_{00}&g_{01}&g_{02}&g_{03}\\g_{10}&g_{11}&g_{12}&g_{13}\\g_{20}&g_{21}&g_{22}&g_{23}\\g_{30}&g_{31}&g_{32}&g_{33} \end{pmatrix} \begin{pmatrix} \Gamma_{\ \mu\nu}^0\\\Gamma_{\ \mu\nu}^1\\\Gamma_{\ \mu\nu}^2\\\Gamma_{\ \mu\nu}^3\end{pmatrix} \] 双対空間の計量テンソルを行列\((g^{\mu\nu})\)とみなすと、その行列は\((g_{\mu\nu})\)の逆行列になるので、 \[\begin{pmatrix} \Gamma_{\ \mu\nu}^0\\\Gamma_{\ \mu\nu}^1\\\Gamma_{\ \mu\nu}^2\\\Gamma_{\ \mu\nu}^3\end{pmatrix} =\begin{pmatrix}g^{00}&g^{01}&g^{02}&g^{03}\\g^{10}&g^{11}&g^{12}&g^{13}\\g^{20}&g^{21}&g^{22}&g^{23}\\g^{30}&g^{31}&g^{32}&g^{33} \end{pmatrix}\begin{pmatrix} \boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu\\\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu\end{pmatrix}\] \[\begin{cases} \Gamma_{\ \mu\nu}^0=g^{00}\boldsymbol{e}_0\cdot \partial_\nu\boldsymbol{e}_\mu+g^{01}\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu+g^{02}\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu+g^{03}\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu \\\Gamma_{\ \mu\nu}^1=g^{10}\boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu+g^{11}\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu+g^{12}\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu+g^{13}\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu \\\Gamma_{\ \mu\nu}^2=g^{20}\boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu+g^{21}\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu+g^{22}\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu+g^{23}\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu \\\Gamma_{\ \mu\nu}^3=g^{30}\boldsymbol{e}_0\cdot\partial_\nu\boldsymbol{e}_\mu+g^{31}\boldsymbol{e}_1\cdot\partial_\nu\boldsymbol{e}_\mu+g^{32}\boldsymbol{e}_2\cdot\partial_\nu\boldsymbol{e}_\mu+g^{33}\boldsymbol{e}_3\cdot\partial_\nu\boldsymbol{e}_\mu \end{cases}\] \(\xi\)成分のクリストッフェルの記号は \[\Gamma_{\ \mu\nu}^\xi=g^{\xi\rho}\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu\tag{1}\] となります。\(\rho\)は縮約の添え字です。\(\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu\)を計量テンソルを使って表していきます。 \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu+\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu)\] \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu+\boldsymbol{e}_\rho\cdot\partial_\mu\boldsymbol{e}_\nu)\] ちょっとトリッキーな変形ですが偏微分の添え字と基底ベクトルが交換できることから成り立ちます。合成関数の微分を使います。 \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\partial_\nu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\mu)-\boldsymbol{e}_\mu\cdot\partial_\nu\boldsymbol{e}_\rho+\partial_\mu(\boldsymbol{e}_\rho\cdot\boldsymbol{e}_\nu)-\boldsymbol{e}_\nu\cdot\partial_\mu\boldsymbol{e}_\rho)\] \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\partial_\nu g_{\rho\mu}-\boldsymbol{e}_\mu\cdot\partial_\nu\boldsymbol{e}_\rho+\partial_\mu g_{\rho\nu}-\boldsymbol{e}_\nu\cdot\partial_\mu\boldsymbol{e}_\rho)\] 基底と偏微分の添え字を交換して\(\rho\)の偏微分に変えます。 \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\partial_\nu g_{\rho\mu}+\partial_\mu g_{\rho\nu}-\boldsymbol{e}_\mu\cdot\partial_\rho\boldsymbol{e}_\nu-\boldsymbol{e}_\nu\cdot\partial_\rho\boldsymbol{e}_\mu)\] \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\partial_\mu g_{\rho\nu}+\partial_\nu g_{\rho\mu}-\partial_\rho(\boldsymbol{e}_\nu\cdot\boldsymbol{e}_\mu))\] \[\boldsymbol{e}_\rho\cdot\partial_\nu\boldsymbol{e}_\mu=\frac{1}{2}(\partial_\mu g_{\rho\nu}+\partial_\nu g_{\rho\mu}-\partial_\rho g_{\mu\nu})\] これを(1)に代入して \[\Gamma_{\ \mu\nu}^\xi=\frac{1}{2}g^{\xi\rho}(\partial_\mu g_{\rho\nu}+\partial_\nu g_{\rho\mu}-\partial_\rho g_{\mu\nu})\] クリストッフェルの記号が計量テンソルのみから表せるので、重力場での軌跡の方程式、測地線方程式\(\frac{du^\mu}{d\tau}+\Gamma_{\ \nu\rho}^\mu u^\nu u^\rho=0\)も計量だけで決まります。重力場での軌跡は時空間の計量で決まります。