楽しい科学（理論）チャンネル

　今回はアインシュタイン方程式を解く準備会です。

　3次元直交座標の\(\vec{r}=(x,y,z)\)について、 ベクトル解析の便利記号 \[\nabla:=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\] を使った公式 \[\nabla\frac{1}{r}=-\frac{\boldsymbol{e}_r}{r^2}\] を示していきます。\(\boldsymbol{e}_r\)は動径方向の単位ベクトルです。 \[\nabla\frac{1}{r}=\left(\frac{\partial}{\partial x}\frac{1}{r},\frac{\partial }{\partial y}\frac{1}{r},\frac{\partial }{\partial z}\frac{1}{r}\right)\] \[=\left(-\frac{1}{r^2}\frac{\partial r}{\partial x},-\frac{1}{r^2}\frac{\partial r}{\partial y},-\frac{1}{r^2}\frac{\partial r}{\partial z}\right)\] \(r=\sqrt{x^2+y^2+z^2}\)なので、 \[\frac{\partial r}{\partial x}=\frac{2x}{2\sqrt{x^2+y^2+z^2}}=\frac{x}{r}\] 他の成分も同様に計算すれば \[\nabla\frac{1}{r}=\left(-\frac{1}{r^2}\frac{x}{r},-\frac{1}{r^2}\frac{y}{r},-\frac{1}{r^2}\frac{z}{r}\right)\] \[=-\frac{1}{r^2}\frac{(x,y,z)}{r}=-\frac{\boldsymbol{e}_r}{r^2}\] これで示せました。

　今原点にのみ物質がある状況を想定してみます。この想定はシュワルツシルト解や万有引力の法則の導出に使います。まずエネルギー運動量テンソルは \[T_{\mu\nu}=\left(\rho+\frac{P}{c^2}\right)u_\mu u_\nu+Pg_{\mu\nu}\] 物質場は原点にしかなく物質同士の接触、相互作用による圧力\(P\)は0となります。また物質は原点で静止しているので、(物質は動いてるかもしれませんが、座標系も同じように移動させています。)４減速度は\(u^\mu\boldsymbol{e}_\mu=(c,0,0,0)\)となります。下付きになっているので\(u_\mu=g_{\mu\nu}u^{\nu}\)平坦な空間で\(u_{\mu}\boldsymbol{e}^\mu=(-c,0,0,0)\)となります。 \[T_{\mu\nu}=\begin{cases}Mc^2/V_{\epsilon}&(\mu,\nu)=(0,0)\ \mathrm{and}\ (x,y,z)\in V_{\epsilon} \\0&(\mu,\nu)=(0,0)\ \mathrm{and}\ (x,y,z)\notin V_{\epsilon} \\0&(\mu,\nu)\neq(0,0)\end{cases}\] \(M\)は物質の質量です。\(V_{\epsilon}\)は物質の分布する領域と体積を表します。エネルギー運動量テンソルはこの条件だけを扱うことにします。

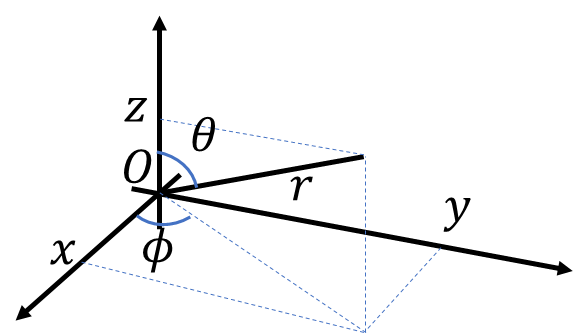
　直交座標\((x,y,z)\)はタテ、ヨコ、タカサを指定して空間の１つの点を決めていました。球面座標系\((r,\theta,\phi)\)は距離、緯度、経度みたいに１つの点を決める座標系です。具体的には、 \[\begin{cases} x=r\sin\theta\cos\phi \\y=r\sin\theta\sin\phi \\z=r\cos\theta \end{cases}\] と決まっています。 物理学では周期運動を表す時には直交座標より球面座標を使った方が楽な場合があります。 \[d\vec{x}=dx\boldsymbol{e}_x+dy\boldsymbol{e}_y+dz\boldsymbol{e}_z\] 微小量ベクトルを座標変換して \[d\vec{x}=dr\boldsymbol{e}_r+d\theta\boldsymbol{e}_\theta+d\phi\boldsymbol{e}_\phi\] を求めてみましょう。\(dx\)を座標変換します。 \[dx=\frac{\partial x}{\partial r}dr+\frac{\partial x}{\partial \theta}d\theta+\frac{\partial x}{\partial\phi}d\phi\] \[dx=\sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi\] 同様にして\(dy,dz\)も求めます。(画面に収めるためタテベクトルになってます。) \[d\vec{x}=\begin{pmatrix} \sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi \\\sin\theta\sin\phi dr+r\cos\theta\sin\phi d\theta+r\sin\theta\cos\phi d\phi \\\cos\theta dr-r\sin\theta d\theta \end{pmatrix}\] \[d\vec{x}=dr\begin{pmatrix} \sin\theta\cos\phi \\\sin\theta\sin\phi \\\cos\theta\end{pmatrix} +d\theta\begin{pmatrix} r\cos\theta\cos\phi \\r\cos\theta\sin\phi \\-r\sin\theta\end{pmatrix} +d\phi\begin{pmatrix} -r\sin\theta\sin\phi \\r\sin\theta\cos\phi \\0 \end{pmatrix}\] これで極座標の基底ベクトルを求めることができました。計量テンソルも求めて見ましょう。\(g_{\mu\nu}=\boldsymbol{e}_\mu\cdot\boldsymbol{e}_\nu\)より \[g_{rr}=\sin^2\theta\cos^2\phi+\sin^2\theta\sin^2\phi+\cos^2\theta\] \[=\sin^2\theta(\cos^2\phi+\sin^2\phi)+\cos^2\theta=1\] \[g_{\theta\theta}=r^2\cos^2\theta\cos^2\phi+r^2\cos^2\theta\sin^2\phi+r^2\sin^2\theta\] \[=r^2(\cos^2\theta+\sin^2\theta)=r^2\] \[g_{\phi\phi}=r^2\sin^2\theta\sin^2\phi+r^2\sin^2\theta\cos^2\phi=r^2\sin^2\theta\] これ以外は０になります。 \[g_{r\theta}=g_{\theta r}=r\sin\theta\cos\theta\cos^2\phi-r\sin\theta\cos\theta\sin^2\phi-r\sin\theta\cos\theta=0\] \[g_{r\phi}=g_{\phi r}=-r\sin^2\theta\sin\phi\cos\phi+r^2\sin^2\theta\sin\phi\cos\phi=0\] \[g_{\theta\phi}=g_{\phi\theta}=r^2\sin\theta\cos\theta\sin\phi\cos\phi-r^2\sin\theta\cos\theta\sin\phi\cos\phi=0\] ちなみに線素ベクトルの内積は、 \[d\vec{x}\cdot d\vec{x}=g_{ij}dx^idx^j\] \[=dr^2+r^2d\theta^2+r^2\sin^2\theta d\phi^2\] となります。

　万有引力の法則を極座標で表してみます。後でアインシュタインの理論から求められる重力とどう違うか比較するため極座標についてちょっとだけ詳しく見てみましょう。万有引力に依る惑星の運動は平面に収まるので、\(\theta=\pi/2\)として\(x,y\)平面運動を制限します。(制限すると言うよりはそのように\(x,y\)平面を取ります。)上の話から、極座標での基底ベクトルは、 \[\boldsymbol{e}_r=(\cos\phi,\sin\phi),\ \boldsymbol{e}_\phi=(-r\sin\phi,r\cos\phi)\] です。偏角方向の単位ベクトルの次元が長さになっていますね。基本的に基底ベクトルは無次元にしたいので、\(\boldsymbol{e}_\phi=(-\sin\phi,\cos\phi)\)とする文献がほとんどですが計量テンソルや、後で出てくるシュワルツシルト時空の測地線方程式の互換が悪くなるので、気にせずこのままいきます。位置、速度、加速度を極座標で表していきます。 \[\vec{x}=\begin{pmatrix}r\cos\phi \\r\sin\phi\end{pmatrix}\] \[\vec{x}=r\boldsymbol{e}_r\] \[\frac{d\vec{x}}{dt}=\begin{pmatrix}\frac{dr}{dt}\cos\phi-r\sin\phi\frac{d\phi}{dt} \\\frac{dr}{dt}\sin\phi+r\cos\phi\frac{d\phi}{dt}\end{pmatrix}\] \[\vec{v}=\frac{d\vec{x}}{dt}=\frac{dr}{dt}\boldsymbol{e}_r+\frac{d\phi}{dt}\boldsymbol{e}_\phi\] \[\frac{d^2\vec{x}}{dt^2}=\begin{pmatrix} \frac{d^2r}{dt^2}\cos\phi-2\frac{dr}{dt}\sin\phi\frac{d\phi}{dt}-r\cos\phi\left(\frac{d\phi}{dt}\right)^2-r\sin\phi\frac{d^2\phi}{dt^2} \\\frac{d^2r}{dt^2}\sin\phi+2\frac{dr}{dt}\cos\phi\frac{d\phi}{dt}-r\sin\phi\left(\frac{d\phi}{dt}\right)^2+r\cos\phi\frac{d^2\phi}{dt^2} \end{pmatrix}\] 動径方向の加速度は、 \[\frac{d^2r}{dt^2}-r\left(\frac{d\phi}{dt}\right)^2\] となります。偏角方向の加速度は、 \[\frac{2}{r}\frac{dr}{dt}\frac{d\phi}{dt}+\frac{d^2\phi}{dt^2}=\frac{1}{r^2}\frac{d}{dt}\left(r^2\frac{d\phi}{dt}\right)\] となります。ちょっとこの式変形は難しいので計算結果から積の微分を使って逆算してみてください。加速度の大きさはあまり使わないので、 \[\vec{\alpha}=\left[\frac{d^2r}{dt^2}-r\left(\frac{d\phi}{dt}\right)^2\right]\boldsymbol{e}_r+\left[\frac{1}{r^2}\frac{d}{dt}\left(r^2\frac{d\phi}{dt}\right)\right]\boldsymbol{e}_\phi\] だけ覚えておきましょう。 距離は、 \[x=\sqrt{\vec{x}\cdot\vec{x}}=\sqrt{g_{rr}r^2}=r\] となります。次に速度は 速さは \[v=\sqrt{\vec{v}\cdot\vec{v}}=g_{rr}\left(\frac{dr}{dt}\right)^2+g_{\phi\phi}\left(\frac{d\phi}{dt}\right)^2\] \[v=\left(\frac{dr}{dt}\right)^2+r^2\left(\frac{d\phi}{dt}\right)^2\] となります。

万有引力 \[\vec{F}=-\frac{GMm}{r^2}\boldsymbol{e}_r+0\boldsymbol{e}_\phi\] と運動方程式 \[m\frac{d^2\vec{x}}{dt^2}=\vec{F}\] から重力場での加速度を極座標で求めることができます。動径方向は \[\frac{d^2r}{dt^2}-r\left(\frac{d\phi}{dt}\right)^2=-\frac{GM}{r^2}\] こうなります。偏角方向は \[\frac{1}{r^2}\frac{d}{dt}\left(r^2\frac{d\phi}{dt}\right)=0\] です。今回の前半の話はアインシュタイン方程式を球対称な条件で解くのに必要になります。