/*　復習

　\((x^0,x^1)\)から\((x'^0,x^1)\)へのローレンツ変換 \[x'^0=\gamma x^0-\beta\gamma x^1\] \[x'^1=-\beta\gamma x^0+\gamma x^1\] 逆変換は \[x^0=\gamma x'^0+\beta\gamma x'^1\] \[x^1=\beta\gamma x'^0+\gamma x'^1\]

終わり　*/

　ただ復習するのも詰まらないので、時空図というものを使ってみよう。特殊相対性理論では、人によって時間や長さが変わるというものであった。それぞれの人が、座標系を持つのである。しかしその人ごとに座標系を用意してあげるのは不便である。そこで１つの平面に表してしまおうという訳だ。仮想的に静止系\(K(x^0,x^1)\)と、一定の速度\(V=c/2\)で等速直線運動する系\(K'(x'^0,x'^1)\)があるとしよう。\(K\)から見ると\(\beta=1/2,\gamma=2/\sqrt{3}\)なので、 \[x'^0=\frac{2}{\sqrt{3}}x^0-\frac{1}{\sqrt{3}}x^1\] \[x'^1=-\frac{1}{\sqrt{3}}x^0+\frac{2}{\sqrt{3}}x^1\] である。\(x^0=ax^1+b\)の形にすると、 \[x^0=\frac{1}{2}x^1+\frac{\sqrt{3}}{2}x'^0\] \[x^0=2x^1-\sqrt{3}x'^1\] ２本の直線の式が得られた。\(x'^0,x'^1=0,1,2\cdots\)と変化させていったものを、静止系\(K\)に書き込むと、

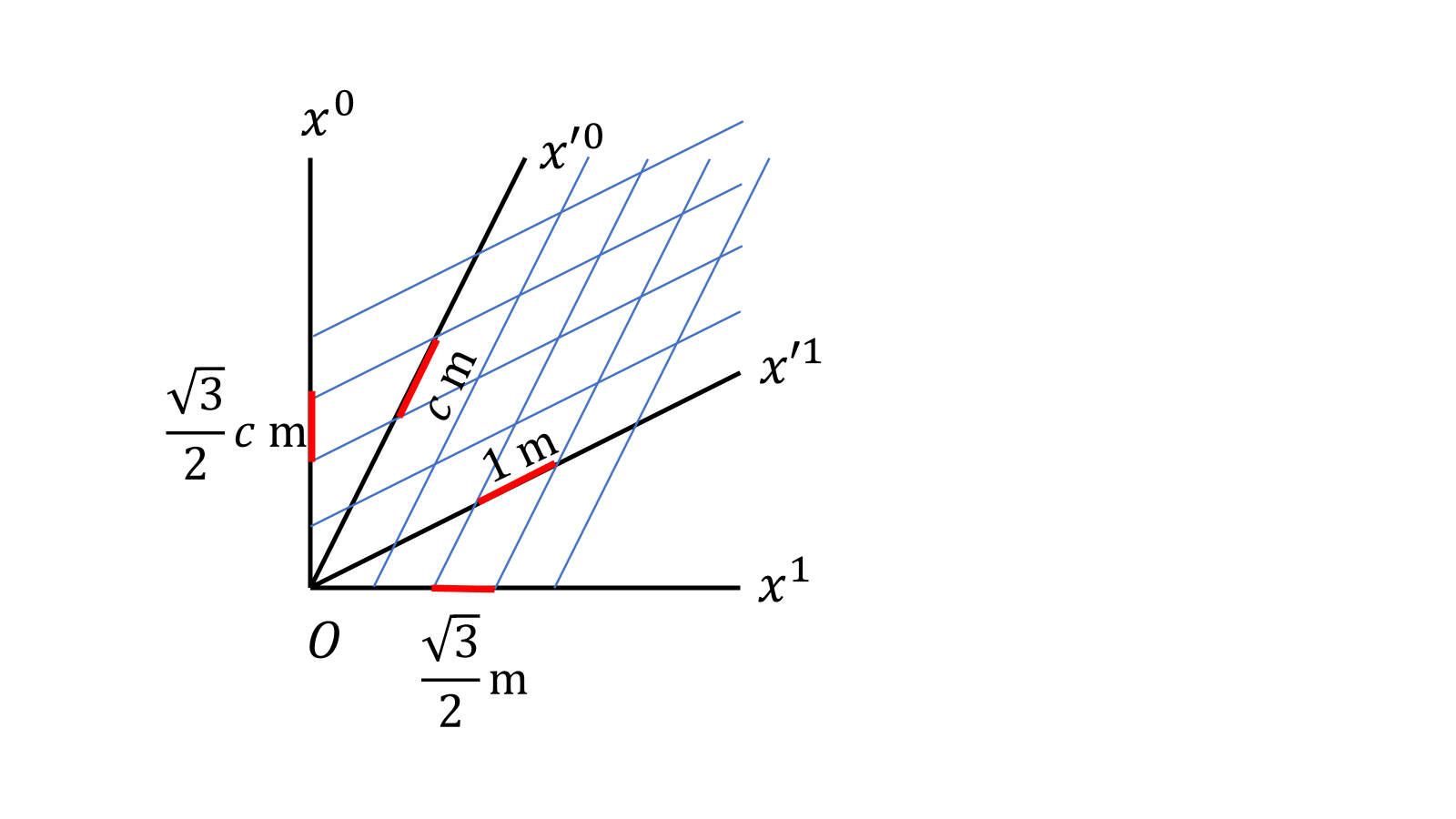
　特に\(x'^0=0\)の直線\(x'^0\)軸、\(x'^1=0\)の直線を\(x'^1\)軸とする。\(K'\)の目盛り(\(x'^0=0,x'^1=0\)とした直線)で\(1\ \mathrm{m}\)測ると、\(\sqrt{3}/2\ \mathrm{m}\)、\(K\)での\(\sqrt{3}/2\)秒は、\(K'\)での\(1\)秒になっている。(図の\(c\)はセンチメートルじゃなくて光の速さです。みずらくてすいません。)このようにすることで、１つの平面で、ローレンツ収縮、時間の遅れを表すことができた。直交座標\(K\)での時空の距離は、 \[(x^0\boldsymbol{e}_0+x^1\boldsymbol{e}_1)\cdot(x^0\boldsymbol{e}_0+x^1\boldsymbol{e}_1)=-(x^0)^2+(x^1)^2\] ローレンツ逆変換をすると、 \[=-\left(\frac{2}{\sqrt{3}}x'^0+\frac{1}{\sqrt{3}}x'^1\right)^2+\left(\frac{1}{\sqrt{3}}x'^0+\frac{2}{\sqrt{3}}x'^1\right)^2\] \[=\frac{-4+1}{3}(x'^0)^2+\frac{-1+4}{3}(x'^1)^2=-(x'^0)^1+(x'^1)^2\] ローレンツ変換後の内積も不変である。しかし、ローレンツ変換後は直交座標になっていない。こちらでの基底ベクトルがどのようになっているか気になるところだ。ある点\(P(x^0,x^1)\)を\(\boldsymbol{e}'_0,\boldsymbol{e}'_1\)を使って表すことを考える。 \[x^0=\frac{2}{\sqrt{3}}x'^0+\frac{1}{\sqrt{3}}x'^1\] \[x^1=\frac{1}{\sqrt{3}}x'^0+\frac{2}{\sqrt{3}}x'^1\] このローレンツ逆変換から、\(\boldsymbol{e}'_0,\boldsymbol{e}'_1\)を求めてみよう。 \[x^0\boldsymbol{e}_0+x^0\boldsymbol{e}_1\] \[=\frac{2}{\sqrt{3}}x'^0\boldsymbol{e}_0+\frac{1}{\sqrt{3}}x'^1\boldsymbol{e}_0+\frac{1}{\sqrt{3}}x'^0\boldsymbol{e}_1+\frac{2}{\sqrt{3}}x'^1\boldsymbol{e}_1\] \[=x'^0\left(\frac{2}{\sqrt{3}}\boldsymbol{e}_0+\frac{1}{\sqrt{3}}\boldsymbol{e}_1\right)+x'^1\left(\frac{1}{\sqrt{3}}\boldsymbol{e}_0+\frac{2}{\sqrt{3}}\boldsymbol{e}_1\right)\] \[=x'^0\boldsymbol{e}'_0+x'^1\boldsymbol{e}'_1\] であるから、 \[\boldsymbol{e}'_0=\frac{2}{\sqrt{3}}\boldsymbol{e}_0+\frac{1}{\sqrt{3}}\boldsymbol{e}_1,\ \boldsymbol{e}'_1=\frac{1}{\sqrt{3}}\boldsymbol{e}_0+\frac{2}{\sqrt{3}}\boldsymbol{e}_1\] \[\boldsymbol{e}'_0=\begin{pmatrix}2/\sqrt{3}\\1/\sqrt{3}\end{pmatrix},\ \boldsymbol{e}'_1=\begin{pmatrix}1/\sqrt{3}\\2/\sqrt{3}\end{pmatrix}\] \(K\)での基底ベクトルを\(\boldsymbol{e}_0=(1,0),\ \boldsymbol{e}_1=(0,1)\)とすると、\(K'\)での基底ベクトルが直交していないのである。しかし、 \[\boldsymbol{e}'_0=\begin{pmatrix}2/\sqrt{3}\\1/\sqrt{3}\end{pmatrix},\ \boldsymbol{e}'_1=\begin{pmatrix}1/\sqrt{3}\\2/\sqrt{3}\end{pmatrix}\] としても、 \[(x'^0\boldsymbol{e}'_0+x'^1\boldsymbol{e}'_1)\cdot(x'^0\boldsymbol{e}'_0+x'^1\boldsymbol{e}'_1)\] \[=\boldsymbol{e}'_0\cdot\boldsymbol{e}'_0(x'^0)^2+2\boldsymbol{e}'_0\cdot\boldsymbol{e}'_1x'^0x'^1+\boldsymbol{e}'_1\cdot\boldsymbol{e}'_1(x'^1)^2\] \[=\frac{-4+1}{3}(x'^0)^2+2\frac{-2+2}{3}x'^0x'^1+\frac{-1+4}{3}(x'^1)^2\] \[=-(x'^0)^2+(x'^1)^2\] 確かにちゃんと成り立っている。慣性系ごとに座標系を割り当てなくても同じ紙一枚に収めることができた。代わりに基底ベクトルが直交しなくなってしまった。計量テンソル\(g'_{ij}=(\boldsymbol{e}'_i\cdot\boldsymbol{e}'_j)\)は変わらず、 \[\begin{matrix}g'_{00}=-1&g'_{01}=0 \\g'_{10}=0&g'_{11}=1\end{matrix}\] となる。