今回の内容は、今回までやってきた内容を逆からたどるだけである。飛ばしてもらってもいい。

終わり　*/

　時間変化しない、弱い重力場と言う条件で、万有引力の法則を求めてみよう。

(1)　重力場を作る天体の条件

\[T_{\mu\nu}=\begin{cases}\rho c^2&(\mu=\nu=0)\\0&(それ以外)\end{cases}\]

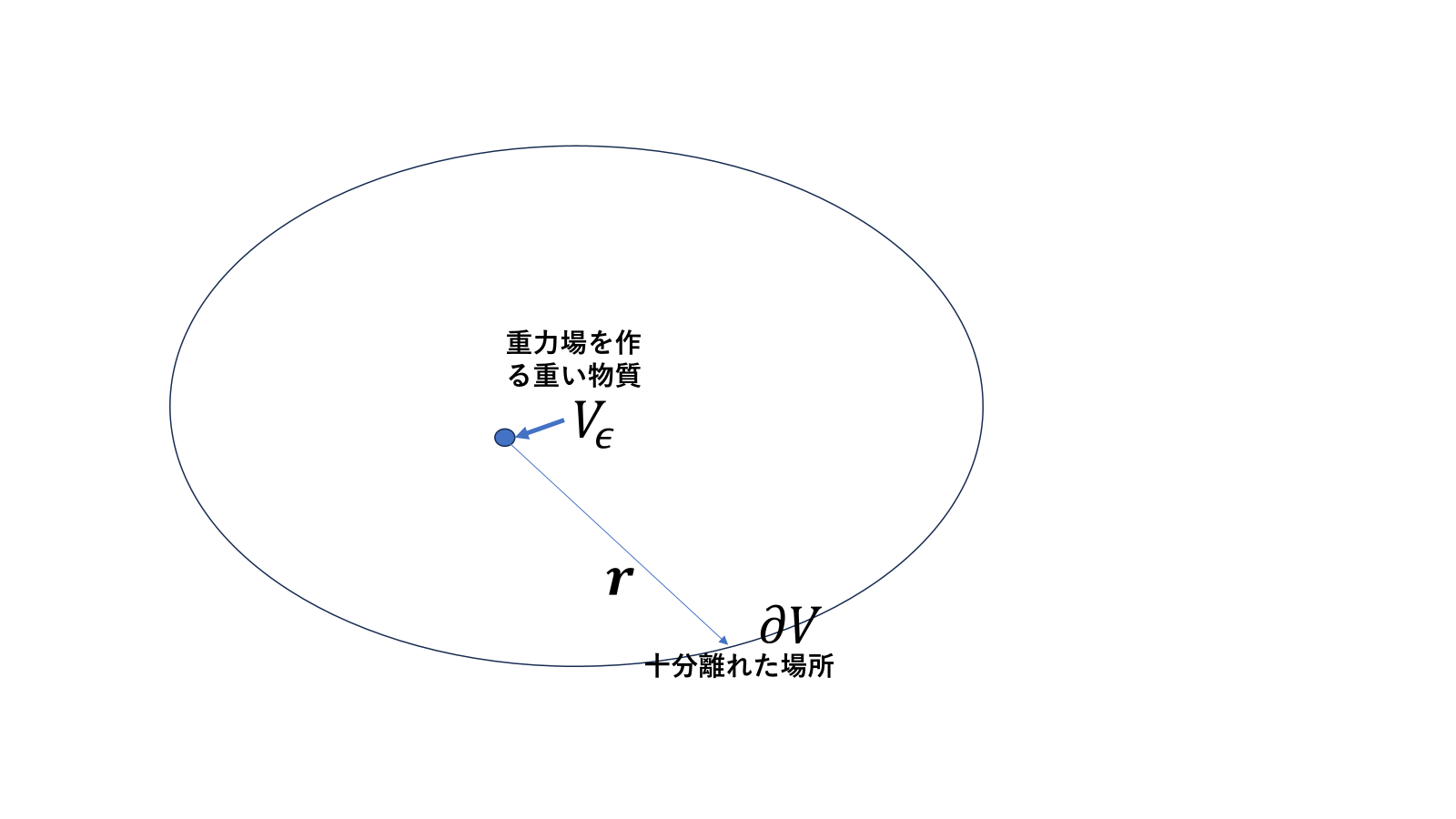
太陽のような天体を想定して条件をもっと詳しく設定すると、天体がある領域を\(V_{\epsilon}\)として \[T_{00}=\rho c^2=\begin{cases}M c^2/V_{\epsilon}&(\boldsymbol{r}\in V_{\epsilon})\\0&(\boldsymbol{r}\notin V_{\epsilon})\end{cases}\] である。相互作用もこの天体を中心に球対称であるとする。

(2)　計量テンソルの条件

　\[g_{\mu\nu}\simeq\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(\mu\neq\nu)\end{cases}\] とする。数字のように扱うが、実際は空間の関数である。行列で表現すると対角行列なので、逆行列である\(g^{\mu\nu}=g_{\mu\nu}\)である。計量は時間変化しない、重力場を作る天体から十分に離れた点では、計量はほぼ\(-1,1,0\)のどれかの値で位置の微分もとても小さい値になる。そのため計量の微分の2次以上は0とみなす。

(3)　軌道を運動する速度の条件

　重力場を進む物体の速度\(v\)は光の速さ\(c\)より十分に小さいとして、 \[d\tau\simeq dt\] \[u^{\mu}\simeq\begin{pmatrix}c\\v_x\\v_y\\v_z\end{pmatrix}\]

　この(1)(2)の条件からアインシュタイン方程式を解いてみよう。まずは計算を楽にするためのテクニック(今回は縮約記法を使って記述するので難しければ前回参照)を使う。 \[G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\] \[R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\] 両辺に計量テンソルの逆行列を掛けると \[g^{\mu\nu}R_{\mu\nu}-\frac{1}{2}Rg^{\mu\nu}g_{\mu\nu}=-\frac{8\pi G}{c^4}(g^{\mu\nu}T_{\mu\nu})\] \[-R=-\frac{8\pi G}{c^4}(g^{\mu\nu}T_{\mu\nu})\] これを使ってもとのアインシュタイン方程式に代入して、リッチスカラーを消去する。 \[R_{\mu\nu}+\frac{1}{2}\frac{8\pi G}{c^4}(g^{\mu\nu}T_{\mu\nu})g_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\] この方程式の\(00\)成分は、運動量エネルギーテンソルを代入すると、 \[R_{00}-\frac{1}{2}\frac{8\pi G}{c^4}(-\rho c^2)(-1)=\frac{8\pi G}{c^4}\rho c^2\] \[R_{00}=\frac{4\pi G}{c^2}\rho\] リッチテンソルの\(00\)成分は、 \[R_{00}=\sum_{\alpha=0}^3\sum_{\beta=0}^3(\partial_\alpha\Gamma^{\alpha}_{\ 00}-\partial_0\Gamma^{\alpha}_{\ 0\alpha}+\Gamma^\alpha_{\ \beta\alpha}\Gamma^{\beta}_{\ 00}-\Gamma^\alpha_{\ \beta0}\Gamma^{\beta}_{\ 0\alpha})\] 条件(2)より計量テンソルが時間変化しない点から第1項目は０となる。計量テンソルの微分の2次以上が０になるため、３、４項目も0になるので、 \[R_{00}=\sum_{\alpha=0}^3\left(\partial_{\alpha}\Gamma^{\alpha}_{\ 00}\right)\] 計量テンソルは時間変化しないので、\(\alpha=0\)の項\(\partial_0\Gamma_{\ 00}^0\)も消えるので、 \[=\sum_{\alpha=1}^3\partial_{\alpha}\sum_{\rho=0}^3\frac{1}{2}g^{\alpha\rho}(\partial_0g_{\rho0}+\partial_0g_{\rho0}-\partial_{\rho}g_{00})\] 時間微分の項は0なので\(\rho=0\)の項も消える。 \[=\frac{1}{2}\sum_{\alpha=1}^3\partial_{\alpha}\sum_{\rho=1}^3g^{\alpha\rho}\partial_{\rho}g_{00}\] \(g^{\mu\nu}\)は\(\mu=\nu=1,2,3\)なら\(1\)、\(\mu\neq\nu\)なら\(0\)だから、 \[R_{00}=\partial_\alpha(\partial_\alpha g_{00})\] \[R_{00}=\frac{1}{2}\nabla^2g_{00}=\frac{4\pi G}{c^2}\rho\] 相互作用がはたらいて天体を中心として、球面領域\(V\)をとる。球面領域の表面\(\partial V\)では空間の歪みが無視できるくらい遠いものとして、両辺を領域\(V\)で両辺を積分すると \[\int_V\nabla\cdot(\nabla g_{00})dV=\frac{8\pi G}{c^2}\int_V\rho dV\] ガウスの定理を左辺に使用して、\(\partial V\)の面積分にすると、 \[\int_{\partial V}(\nabla g_{00})\cdot d\boldsymbol{S}=\frac{8\pi G}{c^2}\cdot M\] \[(\nabla g_{00})\cdot\boldsymbol{e}_r(4\pi r^2)=\frac{8\pi GM}{c^2}\] 球対称な相互作用を考えているので\(\boldsymbol{e}_r//\nabla g_{00}\) \[\nabla g_{00}=\frac{2GM}{c^2r^2}\boldsymbol{e}_r\] 測地線方程式は \[\frac{d u^{\mu}}{d\tau}+\Gamma_{\ \nu\xi}^{\mu}u^{\nu}u^{\xi}=0\] 条件(3)から、\(d\tau=dt,\ u^{\mu}=(c,v_x,v_y,v_z)\)、測地線方程式の\(i=1,2,3\)成分は、 \[\frac{d v^{i}}{dt}+\Gamma_{\ \nu\xi}^{i}u^{\nu}u^{\xi}=0\] \(v_i/c\simeq0\)とみなせるので、(ここでは詳しい計算はしません、測地線方程式のページで同じような計算をしています。) \[\frac{d v^{i}}{dt}+\Gamma_{\ 00}^{i}c^2=0\] アインシュタイン方程式の時のように\(\Gamma^{i}_{00}\)を計算すると \[\frac{d v^{i}}{dt}+\frac{c^2}{2}\partial_ig_{00}=0\] ベクトルの表記を使い、 \[\frac{d\boldsymbol{v}}{dt}=-\frac{c^2}{2}\nabla g_{00}(r)\] アインシュタイン方程式から求めた計量テンソルの微分\(\nabla g_{00}\)を代入すると \[\frac{d\boldsymbol{v}}{dt}=-\frac{GM}{r^2}\boldsymbol{e}_r\] 見事に万有引力の法則を再現できる。まあこうなるよう\(\kappa=8\pi G/c^4\)の値をきめたんですがね。

＊＊一般相対性理論から見た万有引力の法則＊＊

　アインシュタイン方程式 \[G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\] は \[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=1)\\1&(\mu=\nu=1,2,3\\0&(それ以外))\end{cases}\] この３つの条件から万有引力の法則 \[\boldsymbol{F}=m\frac{d\boldsymbol{v}}{dt}=-\frac{GMm}{r^2}\boldsymbol{e}_r\] に帰着する。