楽しい科学(理論)チャンネル
シュワルツシルト解
アインシュタイン方程式を、空間成分が球対称、対角成分無しという条件で解いてみる。これだけ条件を付けても計算量がすごい。ここが一番の山場。解を得るためのテクニックはこれまで紹介してきたもののみであとは根気強さのみでなんとかなる。
/* 補足1 テンソルなど */
**クリストッフェルの記号**
\[\Gamma_{\ \mu\nu}^\lambda:=\sum_{\rho=0}^3\frac{1}{2}g^{\lambda\rho}(\partial_{\mu}g_{\nu\rho}+\partial_{\nu}g_{\mu\rho}-\partial_{\rho}g_{\mu\nu})\]
**リッチテンソル**
\[R_{\mu\nu}=\sum_{\alpha=0}^3\sum_{\beta=0}^3(\partial_\alpha\Gamma^{\alpha}_{\ \mu\nu}-\partial_\nu\Gamma^{\alpha}_{\ \mu\alpha}+\Gamma^\alpha_{\ \beta\alpha}\Gamma^{\beta}_{\ \mu \nu}-\Gamma^\alpha_{\ \beta\nu}\Gamma^{\beta}_{\ \mu\alpha})\]
**リッチスカラー**
\[R=\sum_{\mu=0}^3\sum_{\nu=0}^3g^{\mu\nu}R_{\mu\nu}\]
**運動量エネルギーテンソル**
\[T_{\mu\nu}=\left(\rho+\frac{P}{c^2}\right)u_{\mu}u_{\nu}+Pg_{\mu\nu}\]
**アインシュタインテンソル**
\[G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}\]
/* 補足2 球面座標系 */
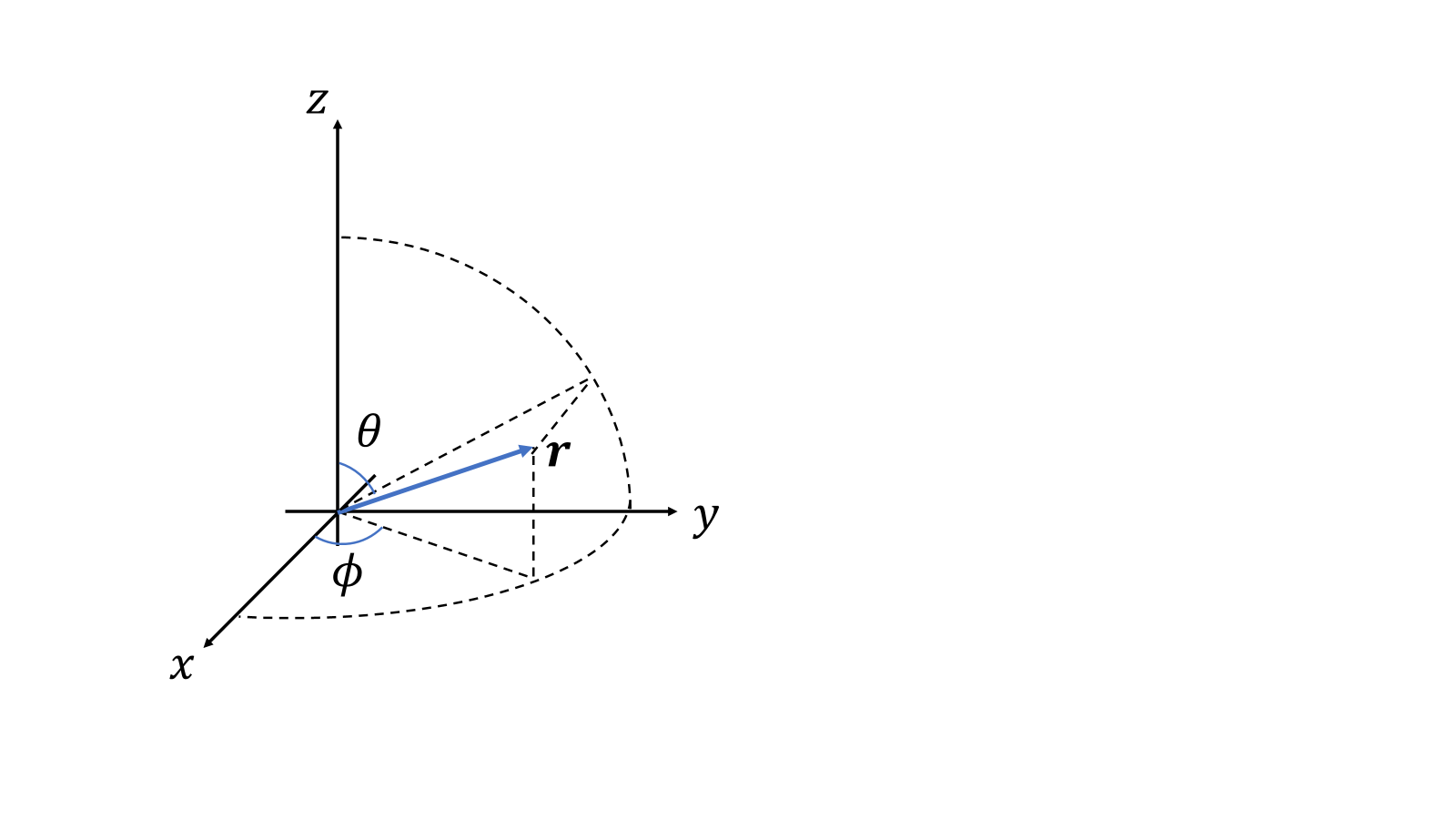 球形座標系\((r,\phi,\theta)\)と直交座標系\((x,y,z)\)の関係は、
\[x=r\sin\theta\cos\phi,\ y=r\sin\theta\sin\phi,\ z=r\cos\theta\]
である。
\[dx=\sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi\]
\[dy=\sin\theta\sin\phi dr+r\cos\theta\sin\phi d\theta+r\sin\theta\cos\phi d\phi\]
\[\ dz=\cos\theta dr-r\sin\theta d\theta\]
となるから、固有時\(\tau\)は
\[-c^2d\tau^2=-(dx^0)^2+dx^2+dy^2+dz^2\]
\[=-(dx^0)^2+(\sin^2\theta\cos^2\phi+\sin^2\theta\sin^2\phi+\cos^2\theta)dr\]
\[+r^2(\cos^2\theta\cos^2\phi+\cos^2\theta\sin^2\phi+\sin^2\theta)d\theta\]
\[+r^2(\sin^2\theta\sin^2\phi+r\sin^2\theta\cos^2\phi)d\phi\]
\[=-(dx^0)^2+dr^2+r^2d\theta^2+r^2\sin^2\theta d\phi^2\]
のように表せる。以上から、直交座標系でのミンコフスキー計量が、
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(その他)\end{cases}\]
であるのに対し、空間成分が球形座標でのミンコフスキー計量は
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
球形座標系\((r,\phi,\theta)\)と直交座標系\((x,y,z)\)の関係は、
\[x=r\sin\theta\cos\phi,\ y=r\sin\theta\sin\phi,\ z=r\cos\theta\]
である。
\[dx=\sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi\]
\[dy=\sin\theta\sin\phi dr+r\cos\theta\sin\phi d\theta+r\sin\theta\cos\phi d\phi\]
\[\ dz=\cos\theta dr-r\sin\theta d\theta\]
となるから、固有時\(\tau\)は
\[-c^2d\tau^2=-(dx^0)^2+dx^2+dy^2+dz^2\]
\[=-(dx^0)^2+(\sin^2\theta\cos^2\phi+\sin^2\theta\sin^2\phi+\cos^2\theta)dr\]
\[+r^2(\cos^2\theta\cos^2\phi+\cos^2\theta\sin^2\phi+\sin^2\theta)d\theta\]
\[+r^2(\sin^2\theta\sin^2\phi+r\sin^2\theta\cos^2\phi)d\phi\]
\[=-(dx^0)^2+dr^2+r^2d\theta^2+r^2\sin^2\theta d\phi^2\]
のように表せる。以上から、直交座標系でのミンコフスキー計量が、
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(その他)\end{cases}\]
であるのに対し、空間成分が球形座標でのミンコフスキー計量は
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
アインシュタイン方程式
\[G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\]
を解くことは容易ではない。そこで
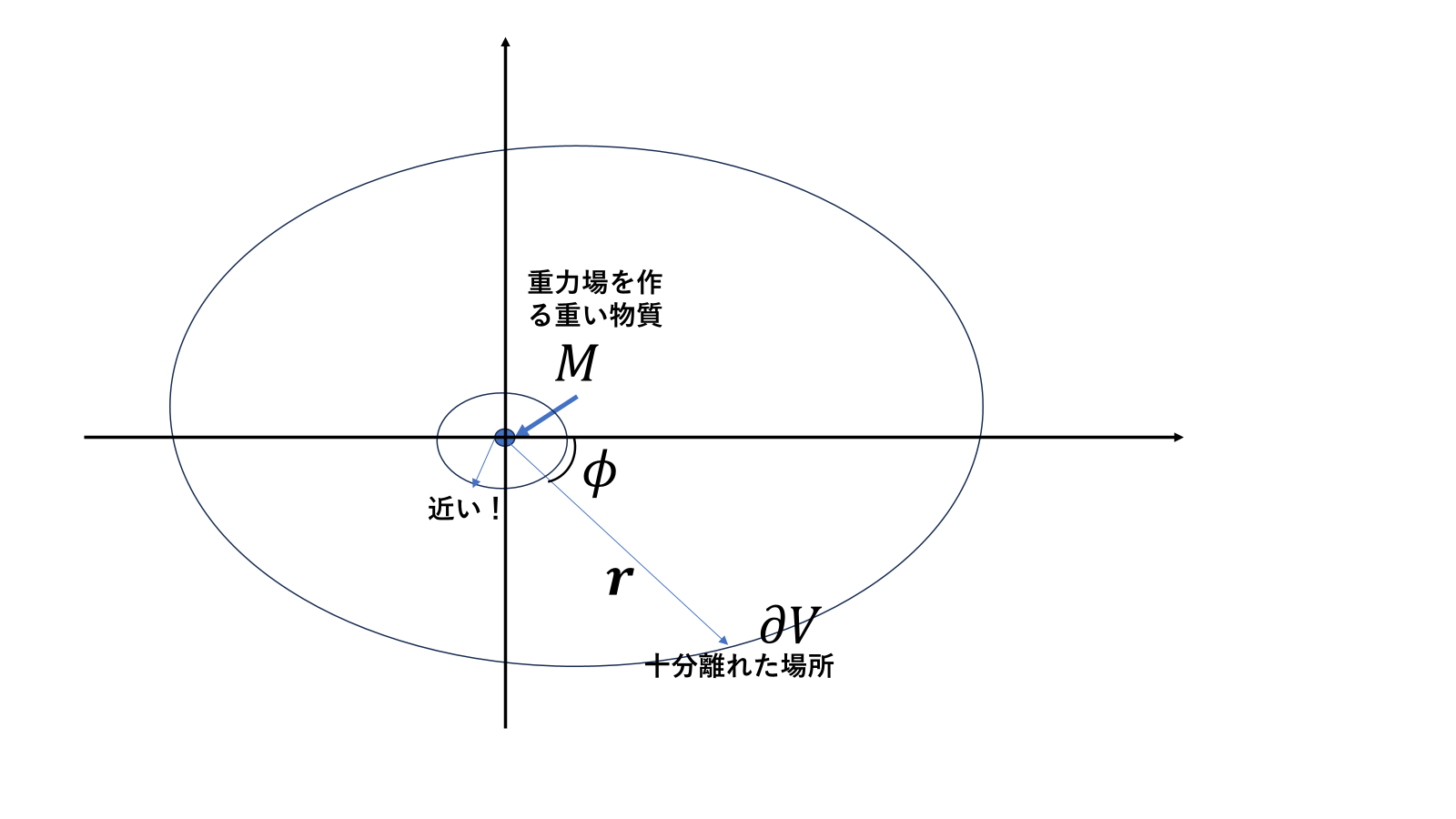
前回は重力場を作る天体から、遠く離れた場所という条件でアインシュタイン方程式を解いたが今回は、そのような条件なしで近場でも通用する解を求めたい。そのまま解くのは無理なので、
(1) 天体の条件
原点\(O\)に天体を配置する。天体の大きさを考えないので、
\[T_{\mu\nu}=\begin{cases}\rho c^2&(r=0)\\0&(r\neq0)\end{cases}\]
今回は\(r\neq0\)で積分もしないので、\(T_{\mu\nu}=0\)と考えてよい。
(2) 計量テンソルの条件
\(\mu\neq\nu\)ならば\(g_{\mu\nu}=0\)(これを仮定しないと\(g^{\mu\nu}\)の計算が大変である。)、球対称な相互作用で\(g_{00},\ g_{rr}\)は、\(r\)のみに依存している。\(\theta,\phi,t\)に依らない。
\[g_{\mu\nu}=\begin{cases}g_{00}(r)&(\mu=\nu=0)\\g_{rr}(r)&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
計量の逆行列\(g^{\mu\nu}\)は、
\[g^{\mu\nu}=\begin{cases}1/g_{00}(r)&(\mu=\nu=0)\\1/g_{rr}(r)&(\mu=\nu=r)\\1/r^2&(\mu=\nu=\theta)\\1/(r^2\sin^2\theta)&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
運動量エネルギーテンソルが\(T_{\mu\nu}=0\)という条件があるので、
\[R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\]
を解くよりは、今回も\(-R=\kappa g^{\mu\nu}T_{\mu\nu}\)を利用して、
\[R_{\mu\nu}=\frac{8\pi G}{c^4}\left(T_{\mu\nu}-\frac{1}{2}(g^{\mu\nu}T_{\mu\nu})g_{\mu\nu}\right)=0\]
つまり、\(R_{\mu\nu}=0\)を解くほうが楽だろう。リッチテンソルを求めるためクリストッフェルの記号を計算しよう。
\[\Gamma_{\ \mu\nu}^\lambda=\sum_{\rho=0}^3\frac{1}{2}g^{\lambda\rho}(\partial_{\mu}g_{\rho\nu}+\partial_{\nu}g_{\mu\rho}-\partial_{\rho}g_{\mu\nu})\]
\(g^{\mu\mu}\)以外は0であるから、クリストッフェルの記号はもっと簡単に、
\[\Gamma_{\ \mu\nu}^\lambda=\frac{1}{2}g^{\lambda\lambda}(\partial_{\mu}g_{\lambda\nu}+\partial_{\nu}g_{\mu\lambda}-\partial_{\lambda}g_{\mu\nu})\]
計量テンソルの微分は、
\[\partial_r g_{00},\ \partial_r g_{rr},\ \partial_r g_{\theta\theta}=2r\]
\[\partial_r g_{\phi\phi}=2r\sin^2\theta,\ \partial_\theta g_{\phi\phi}=2r^2\cos\theta\sin\theta\]
\(\)以外は0である。
\[\Gamma_{\ r0}^{0}=\Gamma_{\ 0r}^{0}=\frac{1}{2}g^{00}\partial_r g_{00}=\frac{\partial_r g_{00}}{2g_{00}}\]
\[\Gamma_{\ 00}^{r}=-\frac{1}{2}g^{rr}\partial_r{g_{00}}=-\frac{\partial_r g_{00}}{2g_{rr}}\]
\[\Gamma_{\ rr}^{r}=\frac{1}{2}g^{rr}\partial_r g_{rr}=\frac{\partial_r g_{rr}}{2g_{rr}}\]
\[\Gamma_{\ \theta\theta}^r=-\frac{1}{2}g^{rr}\partial_r g_{\theta\theta}=-\frac{r}{g_{rr}}\]
\[\Gamma_{\ \phi\phi}^r=-\frac{1}{2}g^{rr}\partial_r g_{\phi\phi}=-\frac{r\sin^2\theta}{g_{rr}}\]
\[\Gamma_{\ r\theta}^\theta=\Gamma_{\ \theta r}^\theta=\frac{1}{2}g^{\theta\theta}\partial_r g_{\theta\theta}=\frac{1}{r}\]
\[\Gamma_{\ \phi\phi}^{\theta}=-\frac{1}{2}g^{\theta\theta}\partial_\theta g_{\phi\phi}=-\sin\theta\cos\theta\]
\[\Gamma_{\ r\phi}^\phi=\Gamma_{\ \phi r}^\phi=\frac{1}{2}g^{\phi\phi}\partial_r g_{\phi\phi}=\frac{1}{r}\]
\[\Gamma_{\ \theta\phi}^\phi=\Gamma_{\ \phi\theta}^\phi=\frac{1}{2}g^{\phi\phi}\partial_\theta g_{\phi\phi}=\frac{\cos\theta}{\sin\theta}\]
それ以外は0になる。ここで先人の力を借りて、
\[g_{00}=-e^{a(r)},\ g_{rr}=e^{b(r)}\]
としよう。\(a\)の\(r\)微分を\(a'\)とすると、クリストッフェルの記号は、
\[\Gamma_{\ r0}^{0}=\frac{a'}{2},\ \Gamma_{\ 00}^{r}=\frac{e^{a-b}a'}{2},\ \Gamma_{\ rr}^{r}=\frac{b'}{2}\]
\[\Gamma_{\ \theta\theta}^r=-re^{-b},\ \Gamma_{\ \phi\phi}^r=-re^{-b}\sin^2\theta,\ \Gamma_{\ r\theta}^\theta=\frac{1}{r}\]
\[\Gamma_{\ \phi\phi}^{\theta}-\sin\theta\cos\theta,\ \Gamma_{\ r\phi}^\phi=\frac{1}{r},\ \Gamma_{\ \theta\phi}^\phi=\frac{\cos\theta}{\sin\theta}\]
よし、リッチテンソルの定義は
\[R_{\mu\nu}=\sum_{\alpha=0}^3(\partial_\alpha\Gamma^{\alpha}_{\ \mu\nu}-\partial_\nu\Gamma^{\alpha}_{\ \mu\alpha}+\Gamma^\alpha_{\ 0\alpha}\Gamma^{0}_{\ \mu \nu}-\Gamma^\alpha_{\ 0\nu}\Gamma^{0}_{\ \mu\alpha}+\Gamma^\alpha_{\ r\alpha}\Gamma^{r}_{\ \mu \nu}\]
\[-\Gamma^\alpha_{\ r\nu}\Gamma^{r}_{\ \mu\alpha}+\Gamma^\alpha_{\ \theta\alpha}\Gamma^{\theta}_{\ \mu \nu}-\Gamma^\alpha_{\ \theta\nu}\Gamma^{\theta}_{\ \mu\alpha}+\Gamma^\alpha_{\ \phi\alpha}\Gamma^{\phi}_{\ \mu\nu}-\Gamma^\alpha_{\ \phi\nu}\Gamma^{\phi}_{\ \mu\alpha})\]
まずは\(R_{00}\)を求めよう。
\[R_{00}=\sum_{\alpha=0}^3(\partial_\alpha\Gamma^{\alpha}_{\ 00}-\partial_0\Gamma^{\alpha}_{\ 0\alpha}+\Gamma^\alpha_{\ 0\alpha}\Gamma^{0}_{\ 00}-\Gamma^\alpha_{\ 00}\Gamma^{0}_{\ 0\alpha}+\Gamma^\alpha_{\ r\alpha}\Gamma^{r}_{\ 00}\]
\[-\Gamma^\alpha_{\ r0}\Gamma^{r}_{\ 0\alpha}+\Gamma^\alpha_{\ \theta\alpha}\Gamma^{\theta}_{\ 00}-\Gamma^\alpha_{\ \theta0}\Gamma^{\theta}_{\ 0\alpha}+\Gamma^\alpha_{\ \phi\alpha}\Gamma^{\phi}_{\ 00}-\Gamma^\alpha_{\ \phi0}\Gamma^{\phi}_{\ 0\alpha})\]
\(0\)にならないクリストッフェルの記号をすべて書き出す。
\[R_{00}=\Gamma^0_{\ r0}\Gamma^{r}_{\ 00}-\Gamma^0_{\ r0}\Gamma^{r}_{\ 00}+\partial_r\Gamma^{r}_{\ 00}-\Gamma^r_{\ 00}\Gamma^{0}_{\ 0r}+\Gamma^r_{\ rr}\Gamma^{r}_{\ 00}\]
\[+\Gamma^\theta_{\ r\theta}\Gamma^{r}_{\ 00}+\Gamma^\phi_{\ r\phi}\Gamma^{r}_{\ 00}=0\]
\[\frac{(a'-b')e^{a-b}a'+e^{a-b}a''}{2}-\frac{e^{a-b}a'^2}{4}+\frac{e^{a-b}a'b'}{4}\]
\[+\frac{e^{a-b}a'}{2r}+\frac{e^{a-b}a'}{2r}=0\]
\(e^{a-b}\neq0\)なので、\(e^{a-b}\)で割って
\[\frac{a''}{2}+\frac{a'^2}{4}-\frac{a'b'}{4}+\frac{a'}{2r}=0\tag{1}\]
\(R_{rr}\)も求める。
\[R_{rr}=\sum_{\alpha=0}^3(\partial_\alpha\Gamma^{\alpha}_{\ rr}-\partial_r\Gamma^{\alpha}_{\ r\alpha}+\Gamma^\alpha_{\ 0\alpha}\Gamma^{0}_{\ rr}-\Gamma^\alpha_{\ 0r}\Gamma^{0}_{\ r\alpha}+\Gamma^\alpha_{\ r\alpha}\Gamma^{r}_{\ rr}\]
\[-\Gamma^\alpha_{\ rr}\Gamma^{r}_{\ r\alpha}+\Gamma^\alpha_{\ \theta\alpha}\Gamma^{\theta}_{\ rr}-\Gamma^\alpha_{\ \theta r}\Gamma^{\theta}_{\ r\alpha}+\Gamma^\alpha_{\ \phi\alpha}\Gamma^{\phi}_{\ rr}-\Gamma^\alpha_{\ \phi r}\Gamma^{\phi}_{\ r\alpha})\]
\(0\)にならないものをすべて書き出す。
\[R_{rr}=-\partial_r\Gamma^{0}_{\ r0}-\Gamma^0_{\ 0r}\Gamma^{0}_{\ r0}+\Gamma^0_{\ r0}\Gamma^{r}_{\ rr}\]
\[-\partial_r\Gamma^{\phi}_{\ r\phi}+\Gamma^\phi_{\ r\phi}\Gamma^{r}_{\ rr}-\Gamma^\phi_{\ \phi r}\Gamma^{\phi}_{\ r\phi}=0\]
\[-\frac{a''}{2}-\frac{a'^2}{4}+\frac{a'b'}{4}+\frac{1}{r^2}+\frac{b'}{2r}-\frac{1}{r^2}=0\]
\[-\frac{a''}{2}-\frac{a'^2}{4}+\frac{a'b'}{4}+\frac{b'}{2r}=0\tag{2}\]
同様に\(R_{\theta\theta}\)は、
\[R_{\theta\theta}=\Gamma^0_{\ r0}\Gamma^{r}_{\ \theta\theta}+\partial_r\Gamma^{r}_{\ \theta\theta}+\Gamma^r_{\ rr}\Gamma^{r}_{\ \theta\theta}-\Gamma^r_{\ \theta\theta}\Gamma^{\theta}_{\ \theta r}\]
\[-\partial_\theta\Gamma^{\phi}_{\ \theta\phi}+\Gamma^\phi_{\ r\phi}\Gamma^{r}_{\ \theta\theta}-\Gamma^\phi_{\ \phi\theta}\Gamma^{\phi}_{\ \theta\phi}=0\]
\[-\frac{a're^{-b}}{2}-(re^{-b})'-\frac{rb'e^{-b}}{2}+e^{-b}\]
\[-\frac{-\sin^2\theta-\cos^2\theta}{\sin^2\theta}-e^{-b}-\frac{\cos^2\theta}{\sin^2\theta}=0\]
\[-\frac{(a'+b')re^{-b}}{2}-(re^{-b})'+1=0\tag{3}\]
(1)式+(2)式より、
\[\frac{a'+b'}{2r}=0,\quad a=-b+c_1\]
\(c_1\)は積分定数。\(a'+b'=0\)を(3)式に代入すると、
\[-(re^{-b})'+1=0,\ re^{-b}=r+c_2,\ e^{-b}=1+\frac{c_2}{r}\]
\[g_{00}=-e^{a}=-e^{-b+c_1}=-e^{c_1}(1+\frac{c_2}{r})\]
(r)が十分大きいときは弱い重力場での計量テンソル\(-1+2GM/(c^2r)\)に一致しなければならないので、初期条件は、
\[c_1=0,\ c_2=-\frac{2GM}{c^2}\]
である。
**シュワルツシルト解(外部)**
時間変化しない球対称な重力場、計量の対角成分は0の初期条件により、アインシュタイン方程式
\[G_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}\]
を解くと、次の解が得られる。
\[g_{\mu\nu}=\begin{cases}-\left(1-\frac{2GM}{c^2r}\right)&(\mu=\nu=0)\\\frac{1}{1-2GM/(c^2r)}&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
 球形座標系\((r,\phi,\theta)\)と直交座標系\((x,y,z)\)の関係は、
\[x=r\sin\theta\cos\phi,\ y=r\sin\theta\sin\phi,\ z=r\cos\theta\]
である。
\[dx=\sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi\]
\[dy=\sin\theta\sin\phi dr+r\cos\theta\sin\phi d\theta+r\sin\theta\cos\phi d\phi\]
\[\ dz=\cos\theta dr-r\sin\theta d\theta\]
となるから、固有時\(\tau\)は
\[-c^2d\tau^2=-(dx^0)^2+dx^2+dy^2+dz^2\]
\[=-(dx^0)^2+(\sin^2\theta\cos^2\phi+\sin^2\theta\sin^2\phi+\cos^2\theta)dr\]
\[+r^2(\cos^2\theta\cos^2\phi+\cos^2\theta\sin^2\phi+\sin^2\theta)d\theta\]
\[+r^2(\sin^2\theta\sin^2\phi+r\sin^2\theta\cos^2\phi)d\phi\]
\[=-(dx^0)^2+dr^2+r^2d\theta^2+r^2\sin^2\theta d\phi^2\]
のように表せる。以上から、直交座標系でのミンコフスキー計量が、
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(その他)\end{cases}\]
であるのに対し、空間成分が球形座標でのミンコフスキー計量は
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
球形座標系\((r,\phi,\theta)\)と直交座標系\((x,y,z)\)の関係は、
\[x=r\sin\theta\cos\phi,\ y=r\sin\theta\sin\phi,\ z=r\cos\theta\]
である。
\[dx=\sin\theta\cos\phi dr+r\cos\theta\cos\phi d\theta-r\sin\theta\sin\phi d\phi\]
\[dy=\sin\theta\sin\phi dr+r\cos\theta\sin\phi d\theta+r\sin\theta\cos\phi d\phi\]
\[\ dz=\cos\theta dr-r\sin\theta d\theta\]
となるから、固有時\(\tau\)は
\[-c^2d\tau^2=-(dx^0)^2+dx^2+dy^2+dz^2\]
\[=-(dx^0)^2+(\sin^2\theta\cos^2\phi+\sin^2\theta\sin^2\phi+\cos^2\theta)dr\]
\[+r^2(\cos^2\theta\cos^2\phi+\cos^2\theta\sin^2\phi+\sin^2\theta)d\theta\]
\[+r^2(\sin^2\theta\sin^2\phi+r\sin^2\theta\cos^2\phi)d\phi\]
\[=-(dx^0)^2+dr^2+r^2d\theta^2+r^2\sin^2\theta d\phi^2\]
のように表せる。以上から、直交座標系でのミンコフスキー計量が、
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=1,2,3)\\0&(その他)\end{cases}\]
であるのに対し、空間成分が球形座標でのミンコフスキー計量は
\[g_{\mu\nu}=\begin{cases}-1&(\mu=\nu=0)\\1&(\mu=\nu=r)\\r^2&(\mu=\nu=\theta)\\r^2\sin^2\theta&(\mu=\nu=\phi)\\0&(その他)\end{cases}\]
