水星の軌道がニュートン力学で予想されている楕円軌道からずれている。このずれを理論的に説明できたのがシュワルツシルト解である。

　重力場上の運動は平面内で記述できるはずなので、前回得たシュワルツシルト解の\(\theta=\frac{\pi}{2}\)として、\(x,y\)平面上での軌跡を求めてみよう。 \[g_{\mu\nu}=\begin{cases}-\left(1-\frac{2GM}{c^2r}\right)&(\mu=\nu=0)\\\frac{1}{1-2GM/(c^2r)}&(\mu=\nu=r)\\r^2&(\mu=\nu=\phi)\\0&(その他)\end{cases}\] 測地線方程式(縮約記法を使っている点に注意。) \[\frac{d^2 x^{\mu}}{d\tau}+\Gamma^{\mu}_{\ \nu\xi}\frac{dx^{\nu}}{d\tau}\frac{dx^{\xi}}{d\tau}=0\] にシュワルツシルト解を代入する。\(2GM/c^2=r_g\)とすると、計量テンソルは、 \[g_{00}=-\left(1-\frac{r_g}{r}\right),\ g_{rr}=\frac{1}{1-r_g/r},\ g_{\phi\phi}=r^2\] 計量テンソルの微分は、 \[\partial_r g_{00}=-\frac{r_g}{r^2},\ \partial_r g_{rr}=\frac{r_g/r^2}{(1-r_g/r)^2},\ \partial_r g_{\phi\phi}=2r\] クリストッフェルの記号は、 \[\Gamma_{\ \nu\xi}^{\mu}=\frac{1}{2}g^{\mu\rho}(\partial_{\nu}g_{\xi\rho}+\partial_{\xi}g_{\nu\rho}-\partial_{\rho}g_{\nu\xi})\] である。計量テンソルの対角成分以外\(0\)なので \[\Gamma_{\ \nu\xi}^{\mu}=\frac{1}{2g_{\mu\mu}}(\partial_{\nu}g_{\xi\mu}+\partial_{\xi}g_{\nu\mu}-\partial_{\mu}g_{\nu\xi})\] \[\Gamma_{\ r0}^0=\Gamma_{\ 0r}^{0}=\frac{\partial_r g_{00}}{2g_{00}},\ \Gamma_{\ 00}^{r}=-\frac{\partial_r g_{00}}{2g_{rr}},\ \Gamma_{\ rr}^{r}=\frac{\partial_r g_{rr}}{2g_{rr}}\] \[\Gamma_{\ \phi\phi}^r=-\frac{\partial_r g_{\phi\phi}}{2g_{rr}},\ \Gamma_{\ \phi r}^\phi=\Gamma_{\ r\phi}^\phi=\frac{\partial_rg_{\phi\phi}}{2g_{\phi\phi}}\] 以外0なので、測地線方程式の時間成分は、 \[\frac{d^2x^0}{d\tau^2}+\Gamma_{0r}^0\frac{dx^0}{d\tau}\frac{dr}{d\tau}+\Gamma_{r0}^0\frac{dr}{d\tau}\frac{dx^0}{d\tau}=0\] \(\Gamma_{\ ij}^k=\Gamma_{\ ji}^k\)なので、 \[\frac{d^2(ct)}{d\tau^2}+2\frac{\partial_rg_{00}}{2g_{00}}\frac{d(ct)}{d\tau}\frac{dr}{d\tau}=0\] 両辺に\(g_{00}/c\)を掛ける。更に\(dA/d\tau=\dot A\)と表すことにすると、 \[\frac{d\dot t}{d\tau}g_{00}+\dot t\frac{\partial g_{00}}{\partial r}\frac{dr}{d\tau}=\frac{d\dot t}{d\tau}g_{00}+\dot t\frac{dg_{00}}{d\tau}=0\] 積の微分の逆を使うと、 \[\frac{d}{d\tau}(\dot tg_{00})=0,\ \dot tg_{00}=-\dot t\left(1-\frac{r_g}{r}\right)=-\varepsilon=const.\tag{3}\] \(-\dot t(1-r_g/r)\)は時空間で\(\tau\)の変化に対して保存量になっている。\(\phi\)成分の測地線方程式は、 \[\frac{d^2\phi}{d\tau^2}+\Gamma_{\ r\phi}^\phi\frac{dr}{d\tau}\frac{d\phi}{d\tau}+\Gamma_{\ \phi r}^\phi\frac{d\phi}{d\tau}\frac{dr}{d\tau}=0\] \[\frac{d\dot\phi}{d\tau}+\frac{\partial_rg_{\phi\phi}}{g_{\phi\phi}}\frac{dr}{d\tau}\frac{d\phi}{d\tau}=0\] 時間成分の時のように両辺に、\(g_{\phi\phi}\)を掛けると、 \[\frac{d\dot\phi}{d\tau}g_{\phi\phi}+\dot\phi\partial_rg_{\phi\phi}\frac{dr}{d\tau}=\frac{d}{d\tau}(\dot\phi g_{\phi\phi})=0\] \[\dot\phi g_{\phi\phi}=r^2\dot\phi=l=const.\tag{4}\] \[r^2d\phi=ld\tau\tag{5}\] \(r^2\dot\phi\)も時空間で保存量である。残るは\(r\)成分の測地線方程式であるが、測地線方程式を解くよりも固有時\(\tau\)の定義を使ったほうが簡単に済むので、そちらを使う。 \[-c^2d\tau^2=g_{\mu\nu}dx^\mu dx^\nu\] \[-c^2d\tau^2=g_{00}c^2dt^2+g_{rr}dr^2+g_{\phi\phi}d\phi^2\] 両辺を\(d\tau^2\)で割ると、 \[-c^2=g_{00}c^2\dot t^2+g_{rr}\dot r^2+g_{\phi\phi}\dot \phi^2\] (3)(4)式を代入して、 \[-c^2=\frac{1}{g_{00}}c^2\varepsilon^2+g_{rr}\dot r^2+\frac{1}{g_{\phi\phi}}l^2\] 両辺を\(g_{rr}\)で割ると、 \[\frac{1}{g_{00}g_{rr}}c^2\varepsilon^2+\dot r^2+\frac{1}{g_{\phi\phi}g_{rr}}l^2+\frac{c^2}{g_{rr}}=0\] \[-c^2\varepsilon^2+\dot r^2+\frac{1}{r^2}\left(1-\frac{r_g}{r}\right)l^2+c^2\left(1-\frac{r_g}{r}\right)=0\] \(1/r=u\)とおくと、\(dr=-du/u^2\) \[\left(\frac{1}{u^2}\frac{du}{d\tau}\right)^2+u^2(1-r_gu)l^2-r_gc^2u+c^2(1-\varepsilon^2)=0\] (5)式から、\(\tau\)を消去する。 \[\left(l\frac{du}{d\phi}\right)^2+(u^2-r_gu^3)l^2+r_gc^2u+c^2(1-\varepsilon^2)=0\] \[\left(\frac{du}{d\phi}\right)^2-\frac{2GM}{c^2}u^3+u^2-\frac{2GM}{l^2}u+\frac{c^2(1-\varepsilon)}{l^2}=0\] 両辺を\(\phi\)で微分すると、 \[\left(2\frac{du}{d\phi^2}-\frac{6GM}{c^2}u^2+2u-2\frac{GM}{l^2}\right)\frac{du}{d\phi}=0\] \[\frac{d^2u}{d\phi^2}-\frac{3GM}{c^2}u^2+u-\frac{GM}{l^2}=0\] この微分方程式を解くことはできないが強い重力場での惑星(特に太陽に近い水星)の運動をよく記述できている方程式である。

＊＊シュワルツシルト時空での惑星の軌道＊＊

　重力場を作る天体を原点\(O\)に配置したとき、惑星の軌道は、\(u=1/r\)として、 \[\frac{d^2u}{d\phi^2}-\frac{3GM}{c^2}u^2+u-\frac{GM}{l^2}=0\] の微分方程式の解となる軌道を取る。

　今回は\(d\tau\simeq dt\)の近似も行っていないので、光もこの経路を取る。

/*　おまけ　近日点の移動

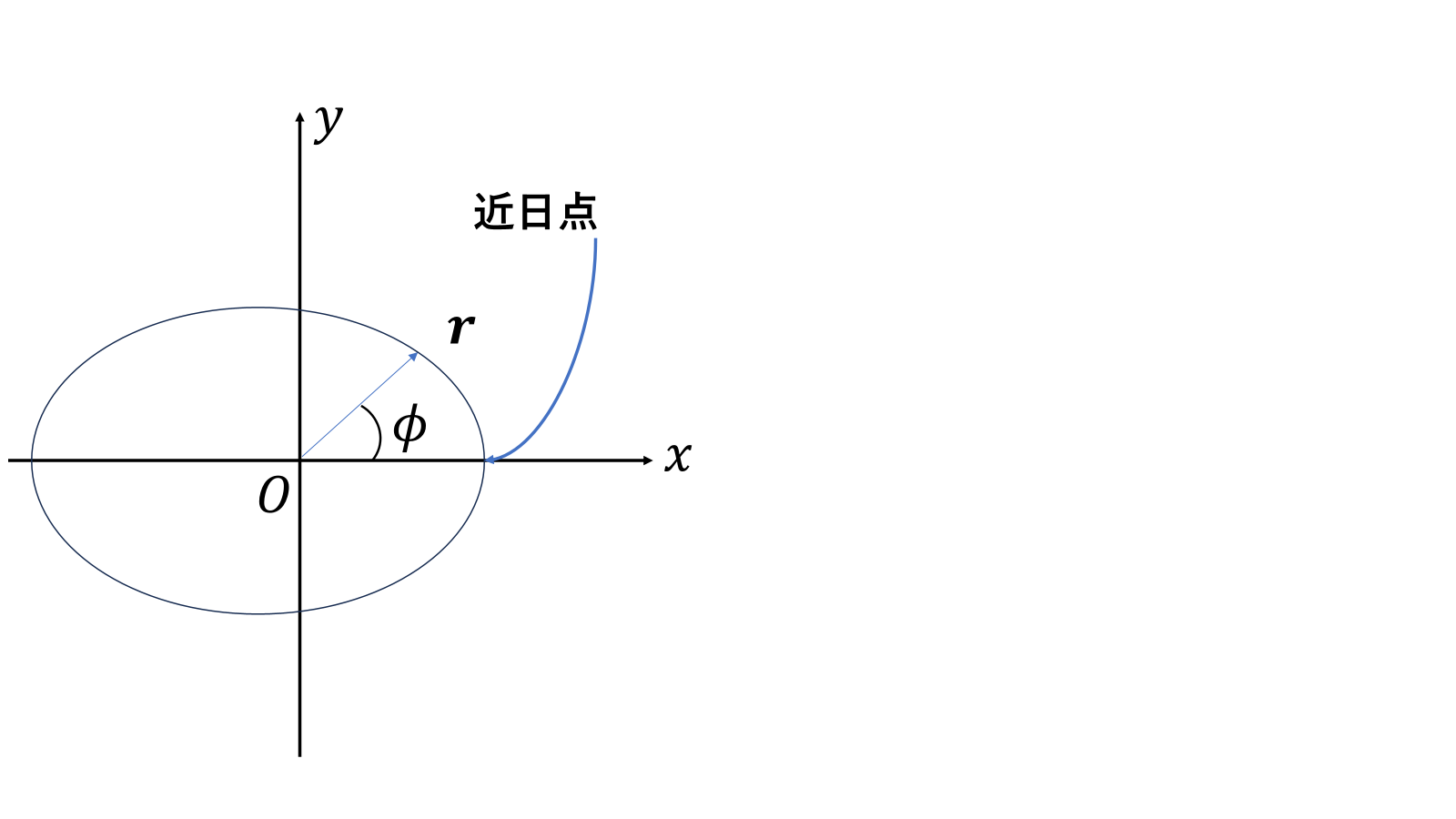
近日点とは、惑星が太陽に一番近くなる点のことを言う。古典力学で導かれる軌跡の方程式、 \[\frac{d^2u}{d\phi^2}+u-\frac{1}{A}=0\] の解は、 \[r=\frac{1}{u}=\frac{A}{1+e\cos\phi}\tag{6}\] の楕円軌道になり、何周しても同じ近日点を通るはずである。しかし、水星の近日点は、公転するごとに少しずつずれている。相対性理論の惑星軌道の微分方程式 \[\frac{d^2u}{d\phi^2}-\frac{3GM}{c^2}u^2+u-\frac{GM}{l^2}=0\] を解くことはできないが、 \[u=\frac{1+e\cos\eta\phi}{A}\tag{7}\] のような解を仮定して、大雑把に近日点がどれ程ずれるのか計算してみよう。\(l=r^2d\phi/d\tau,L_m=r^2d\phi/dt\)の違いがあるが、天体の速度が光の速さより十分小さいとして、\(L_m=l\)とみなすと、 \[\frac{d^2u}{d\phi^2}-\frac{3GM}{c^2}u^2+u-\frac{1}{A}=0\] これに大雑把な解を代入する。 \[-\frac{\eta^2e}{A}\cos\eta\phi-\frac{3GM}{A^2c^2}(1+e\cos\eta\phi)^2+\frac{e\cos\eta\phi}{A}=0\] ほぼ円の軌道とみなすと、離心率\(e\)は0に近いので、\(e^2\simeq0\)とみなす。 \[\frac{1-\eta^2}{A}e\cos\eta\phi-\frac{3GM}{A^2c^2}(1+2e\cos\eta\phi)=0\] この式を\(\phi\)で微分して、 \[-\left(\frac{1-\eta^2}{A}-\frac{6GM}{A^2c^2}\right)\eta e\sin\eta\phi=0\] \[1-\eta^2=\frac{6GM}{Ac^2},\ \eta=\sqrt{1-\frac{6GM}{Ac^2}}\] (6)式、(7)式はほぼ一緒なので、\(\eta\simeq1\)つまり、\((6GM/Ac^2)^2\simeq0\)であるということになるから、\((1+\delta)^n\simeq1+n\delta\)を用いて \[\eta=\sqrt{1-\frac{6GM}{Ac^2}}\simeq1-\frac{3GM}{Ac^2}\] 古典力学での奇跡の方程式で、次の近日点まで1周するのに\(\phi=2\pi\)であるのに対して、相対性理論では、\(2\pi\eta\)だけ進むので近日点のずれは、 \[2\pi-2\pi\eta=\frac{6\pi GM}{Ac^2}\] だえんきどうではないのだが、長半径を\(a\)とすると、 \[2a=r_{\max}+r_{\min}=A/(1-e)+A/(1+e)=\frac{2A}{1-e^2}\] であるから近日点のすれは、 \[2\pi (1-\eta)=\frac{6\pi GM}{(1-e^2)ac^2}\] とも表せる。この計算が観測値の水星の近日点のずれとクリティカルヒットして、一般相対性理論が信じられるようになっていった。

終わり　*/