今回は計算少なめで優しい。一般相対性理論で紹介したいことはだいたい終わったが、シュワルツシルト解を求めた時点ですぐさま分かる内容を触れていなかった。原点\(O\)に質量\(\)をもつものを配置した空間をシュワルツシルト時空といい、\(t,r,\phi\)の3次元で考えると固有時は\(\tau\) \[-c^2d\tau^2=-\left(1-\frac{2GM}{c^2r}\right)c^2dt^2+\frac{1}{1-2GM/(c^2r)}dr^2+r^2d\phi^2\] のように表せる。重力場での時間の遅れはとても簡単にわかる。

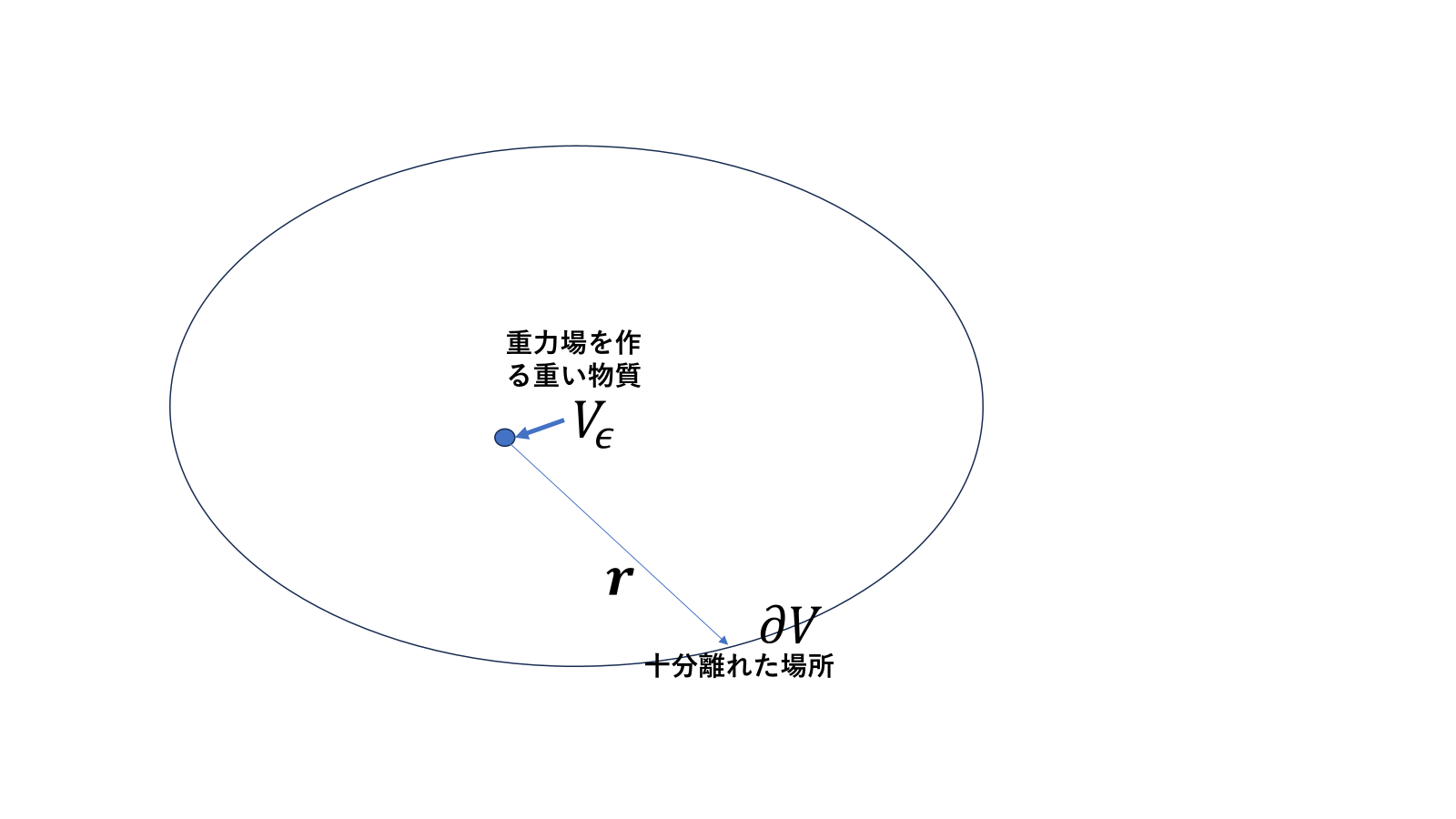
　この図は使いまわしである。重力場の影響がある地点\((R,\phi_0)\)で静止している\(dr=d\phi=0\)ときの固有時は \[d\tau=\sqrt{1-\frac{2GM}{c^2R}}dt\tag{1}\] \(2GM/(c^2r)\)の項が無視できるくらい遠い場所での固有時は、 \[d\tau=dt'\tag{2}\] であるから、(1)(2)式を積分して、 \[\sqrt{1-\frac{2GM}{c^2R}}t=t'\tag{3}\] ちょっと大げさな例で\(\sqrt{1-2GM/c^2R}=0.5\)とかだと、重力場での１年が、無重力の地点での半年になったりする。地球くらいの重力ではそんなに変わらないと思うが、人工衛星とのやり取りでの時間の遅れは相対性理論が計算で使われているらしい。wikiによると、地上と人工衛星で100億分の何秒とからしい。日常で重力場での時間の遅れを体感できるような場面はなさそうだ。 \[-c^2d\tau^2=-\left(1-\frac{2GM}{c^2r}\right)c^2dt^2+\frac{1}{1-2GM/(c^2r)}dr^2+r^2d\phi^2\] ところで、\(r\to 2MG/c^2\)に近づけていくとどうなるだろうか、\(dr^2\)の項が無限に大きくなるだろう。 \[r_g=\frac{2GM}{c^2}\] には特別な名前があり、シュワルツシルト半径という。 \[\sqrt{1-\frac{2GM}{c^2r}}t=1\ \mathrm{yr}\] (3)式から分かる通り、\(r\to r_g\)の極限で無重力での1年が、２年、３年、、、と永遠の時間になってしまう。あと３歩でシュワルツシルト半径から出られるような状況でも、３歩踏み出すのに永遠の時間がかかってしまうため、外に出ることはできない。まあそもそもシュワルツシルト半径の内部に入る前に外の時間に対して発散してしまうのだが、、、地球のシュワルツシルト半径を計算してみよう。 \[\frac{2GM}{c^2}=\frac{2\times6.6743\times10^{-11}\ \mathrm{m^3\ kg^{-1}\ s^{-2}}\times5.972\times10^{24}\ \mathrm{kg}}{(2.99792458\times10^8\ \mathrm{m\ s^{-1}})^2}\] \[\simeq8.87\times10^{-2}\ \mathrm{m}\] 地球のシュワルツシルト半径が約\(9\ \mathrm{mm}\)である。ここまで圧縮した地球表面では、時間が発散している。このように超密度の天体をブラックホールという。なぜブラックホールという名前が付いているかというと、ふつう天体は、自ら光を発するまたは、光を反射するため見ることができる。しかし、シュワルツシルト半径以上に圧縮されている天体は、天体の表面で光が止まってしまうので、観測者にその星の光が届かず、真っ黒に見えるはず、、、そのためブラックホールというのだろうか。このような天体が銀河の中心にあるという話を聞いたことがあるが詳しいことは、分かりません。あともう一つ説明し忘れていたことがあって、赤方偏移という現象である。人間が可視可能な光に限った話ではないが、光の色は振動数\(\nu\)によって決まる。振動数の高いほうから紫外線、紫色、青、緑、黄色、オレンジ、赤、赤外線となっている。(紫外線と赤外線は人には見えない。) \[\nu:=\frac{1}{T}\] 振動数は周期\(T\)の逆数で定義される。強い重力場では時間が遅れるので、周期が大きくなり逆数の関係にある振動数は小さくなる。そのため本来観測されるはずの色よりも低い振動数の色に見えるという現象もある。光が波の性質を持っているという説明は、量子力学のページを作ったときに説明しようかな。

/*　おまけ　*/

　古典力学の範囲でも、 \[\frac{1}{2}mc^2-\frac{GMm}{r_g}\le0\] 光の質量がないのでおかしな式であるが、万有引力のポテンシャルが光速度で運動する物体の運動エネルギーを上回る天体という条件から、 \[\frac{r_g}{GMm}\le\frac{2}{mc^2}\] \[r_g\le\frac{2MG}{c^2}\] ブラックホールの半径を出すことができる。